Итерационный процесс расчёта параметров равновесия

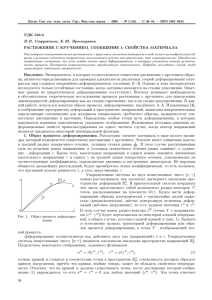
ИТЕРАЦИОННЫЙ ПРОЦЕСС РАСЧЁТА ПАРАМЕТРОВ РАВНОВЕСИЯ
КОНСТРУКТИВНОГО ЭЛЕМЕНТА ПРИ ЕГО КРУЧЕНИИ С РАСТЯЖЕНИЕМ В
УСЛОВИЯХ ЖЁСТКОГО НАГРУЖЕНИЯ
Е.Ю. Просвиряков, В.В. Стружанов
Институт машиноведения УрО РАН, Екатеринбург, Россия
Известно, что решение нелинейных краевых задач механики деформируемого
твёрдого тела является трудной задачей. Как правило, невозможно найти аналитическое
решение и поэтому приходится использовать приближённые (итерационные) методы.
Сходимость итерационных процессов является достаточным условием определения
напряжённо-деформированного состояния. Иными словами, если вычислительный метод
сходится, то он однозначно определяет физическое состояние тела, в противном случае
(расходимости метода) – эта связь, как правило, не просматривается. В данном сообщении
на примере расчёта параметров равновесия конкретной механической системы излагается
один вариант метода упругих решений. Эта модификация обладает тем преимуществом,
что её можно применять к задачам с невыпуклым потенциалом напряжений и, кроме того,
сходимость и расходимость методики увязывается с устойчивостью квазистатического
деформирования.
Рассмотрим конструктивный элемент, осуществляющий растяжение с кручением
упругопластического полого цилиндрического образеца 3 (рис. 1). Стержень 1 работает
только на растяжение (кручение блокировано), стержень 2 – на кручение. Точкам сечения
A–A задаётся монотонно возрастающее перемещение u, а в сечении D–D задан
монотонно возрастающий угол закручивания  . Жёсткости стержней 1 и 2 при
растяжении с кручением соответственно равны 1 и 2 . Таким образом, осуществляется
жёсткое нагружение механической системы. Свойства материала образца описываются
потенциалом напряжений  ( ,  ), который в одной части первого квадранта плоскости
O , примыкающей к началу координат, является выпуклым, а в остальной части –
невыпуклым. Невыпуклость потенциала связана с разупрочнением материала. Здесь
 ,    2e ,  ,  – соответственно деформации растяжения и сдвига образца.
Рис. 1
Поскольку данная механическая система при активном нагружении является
градиентной, то, учитывая специальные геометрические размеры образца, состояние
механической системы опишем потенциальной функцией
1  u   
2
2    
2

   ,   .
2
2
Положения равновесия механической системы определяют критические точки функции
W , которые являются решением уравнения  2W  0. Здесь 2 – оператор Гамильтона,
W
2
определённый в пространстве параметров состояния
e , совпадающем при данном
способе нагружения с пространством деформаций. Расписывая это векторное уравнение,
получим систему двух нелинейных уравнений
W,   ( ,  )  1 (u   )  0,

W,   ( ,  )  2 (   )  0.
Здесь    , – напряжение растяжения,    , – касательное напряжение.
Для облегчения построения итерационного алгоритма запишем систему уравнений
равновесия в векторно-матричной форме
e  q  p  0,
(1)
 0 
где матрица    1
 , а векторы e, p, q соответственно имеют компоненты  ,   ,
 0 2 
 ,  ,  u,  .
E 0 
p
Используя равенство p = C (e  e p ), где C  
 , e – вектор, компонентами
 0 G
которого являются пластические составляющие полных деформаций ( E , G – модули
Юнга и сдвига в упругой области), преобразуем уравнение (1) к виду
(2)
e  q  C (e  e p )  0.
Решение уравнения (2) можно разделить на решение двух задач: основной и
корректирующей. Основная и корректирующая задачи соответственно задаются
равенствами
  q  C   0 и   C (  e p )  0.
Разрешаем данные уравнения и получаем решение основной и корректирующих задач:
p
  P1q и   PC
1 e .
 1

0 
 E
1
 . Непосредственной подстановкой убеждаемся, что
Здесь P1     C    1

1 
 0
2  G 

при известных значениях компонент векторов q и e p решение исходной задачи
определяется как сумма решений основной и корректирующей задач ( e     ). Отметим,
что основная задача является чисто упругой задачей и её решение является первым
приближением к искомому решению. Поскольку материал образца является
упругопластическим, то необходима корректировка первого приближения (основной задачи).
Данная корректировка происходит на основе выделения приращения пластических
деформаций с использованием инкрементального закона пластичности de p  I 2  SC p de,


 1 0
записанного через разностные операторы e p  I 2  SC p (* ,  * ) e . Здесь I  
,
 0 1
c 
c
C p   11 12  , Матрица C p является матрицей жёсткости (матрицей инкрементальных
 c21 c22 


модулей материала – c11   , , c12  c21   , , c22   , . Дискретный аналог получается
интегрированием его на отрезке *   ,  *    с последующим разложением в ряд
Тейлора, в котором затем используется первый линейный член. В результате получаем
выражения
c ( ,  )
c ( ,  )
 c ( ,  ) 
 c ( ,  ) 
 p  1  11 * *    12 * *  ,  p   21 * *   1  22 * *   ,
E
E
G
G




которые в векторно-матричной форме записаны выше. Сумма решений основной и
корректирующей задачи – второе приближение. Третье приближение получаем как сумму
решений основной и двух корректирующих задач. Вторая корректировка получается при
подстановке второго приближения в дискретный закон пластичности и т. д.
Данный итерационный процесс записывается в виде степенного матричного ряда
n
n
k 1
i 1
p
en   B n 1 . Здесь B0  I 2 , B k   Ak i  k  N  , где Aj  PC
1 ( I 2  SC j )  j  N  0 –
это матрица, получающаяся из матрицы
 E  c11
  E
p
 1
A  PC
1 ( I  SC ) 
 c21
  G
 2
c12 
1  E 

G  c22 
2  G 
после вычисления инкрементальных модулей c11 , c22 , c12 для соответствующих значений
деформаций.
Решения характеристического уравнения этой матрицы – вещественные числа.
Поэтому в данном уравнении возможно провести такую замену переменной (дробнолинейное преобразование), что если корни преобразованного уравнения будут лежать в
интервале  ,0 , если корни исходного характеристического расположены в интервале
(-1, 1). Таким образом, задачу об изучении спектра свели к решению модифицированной
проблемы Рауса-Гурвица. При решении проблемы Рауса-Гурвица получена система
линейных неравенств
 a  b  1  0,

1  b  0,
1  a  b  0.

Доказано, что в полученной системе только одно неравенство является определяющим, а
именно, 1  a  b  0. Остальные неравенства вытекают из него. Невыполнение данного
неравенства на каком-то шаге означает, что построенный итерационный метод начнёт
расходиться. Также была изучена сходимость вычислительного метода в том случае, когда
собственное значение матрицы, формирующей ряд, равно единице. Показано, что
сходимость метода в этом случае зависит от жёсткостей стержней, входящих в состав
конструктивного элемента, и от пути нагружения. Приведены соответствующие оценки.
Наконец, было проведено исследование соответствия между вычислениями и
физической реализацией системы. Получено и обосновано, что расходимость
итерационного метода начинается в тот самый момент, когда происходит потеря
устойчивости процесса деформирования механической системы.
Работа выполнена при финансовой поддержке РФФИ (проект 07-08-00125)
ЛИТЕРАТУРА
1. Стружанов В.В., Миронов В.И. Деформационное разупрочнение материала в
элементах конструкций. – Екатеринбург: Изд-во УрО РАН, 1995. – 192 с.