C2 № 484562. В кубе найдите косинус угла между плоскостями и

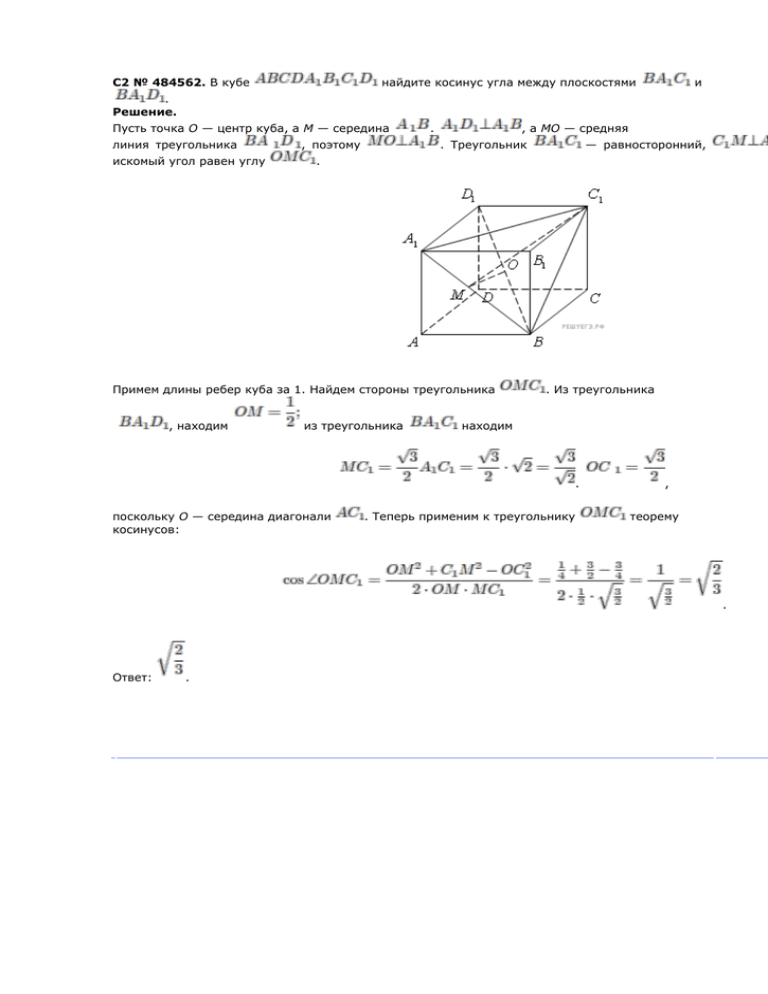
C2 № 484562. В кубе
найдите косинус угла между плоскостями
и
.
Решение.
Пусть точка O — центр куба, а M — середина
линия треугольника
искомый угол равен углу
, поэтому
.
, а MO — средняя
. Треугольник
Примем длины ребер куба за 1. Найдем стороны треугольника
, находим
— равносторонний,
.
из треугольника
. Из треугольника
находим
.
поскольку O — середина диагонали
косинусов:
. Теперь применим к треугольнику
,
теорему
.
Ответ:
.
C2 Сторона основания правильной треугольной призмы
Найдите угол между плоскостью
Решение.
Обозначим
Так как треугольник
и
перпендикулярны
линейный угол двугранного угла с гранями
Из треугольника
Из треугольника
Из треугольника
Искомый угол равен
Ответ:
середину ребра
равносторонний, а треугольник
равнобедренный, отрезки
найдем
найдем
найдем:
равна 2, а диагональ боково
и плоскостью основания призмы.
и
(см. рис.).
—
Следовательно,
—
C2 В прямоугольном параллелепипеде
между плоскостями ABC и
Решение.
известны ребра:
,
.
Плоскости ABC и
имеют общую прямую BD.
Проведем перпендикуляр AH кBD. По теореме о трех перпендикулярах
линейный угол двугранного угла, образованного плоскостями ABC и
угол
. Значит,
, — это
. Из прямоугольного треугольника BAD находим:
.
Из прямоугольного треугольника
находим:
.
Значит,
Ответ:
искомый
.
угол
,
C2 № 484558. В прямоугольном параллелепипеде
. Найдите объем пирамиды
Решение.
заданы длины ребер
если M — точка на ребре
Заметим, что
, причем
.
Площадь прямоугольного треугольника, лежащего в основан
произведения
катетов
Основание пирамиды лежит в плоскости
из точки
того,
, поэтому высотой пирамиды будет являться перпенд
на эту плоскость. Опустим перпендикуляр
что
,
Треугольник AME подобен треугольнику
отрезок
на прямую
. Поскольку
является
высотой
, значит,
.
Ответ: 50.
,
и
пира
C2 В правильной треугольной пирамиде SABC с основанием ABC известны ребра
образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC.
Решение.
Пусть M и N — середины ребер AS и BC соответственно. AN — медиана правильного треугольника A
находится по формуле
. Прямая AS проектируется на плоскость основания и п
проекция точки M — точка
угол
— искомый.
где O —
Тогда
— лежит на отрезке AN. Значит, прямая AN является проекцией прямой
центр
основания,
и
Из прямоугольного треугольника
Значит,
Ответ:
значит,
—
средняя
линия
треугольника ASO поэто
Из прямоугольного треугольника
находим:
искомый
угол
находим:
C2 В правильной треугольной SABC пирамиде с основанием ABC известны ребра
. Найдите угол, образованный плоскостью основания и прямой,
проходящей через середины ребер AS иBC.
Решение.
Пусть N — середина ребра BC, а M — середина AS. Прямая AS проецируется на плоскость
основания в прямую AN. Поэтому проекция точки M — точка
— лежит на отрезке AN.
Значит, прямая AN является проекцией прямойAM, следовательно, угол
искомый. Поскольку
треугольника SAO.
, где O — центр основания,
—
— средняя линяя
Тогда
Кроме того,
Из прямоугольного треугольника
находим:
.
Ответ:
.
C2 В правильном тетраэдре ABCD найдите угол между высотой тетраэдра DH и
медианой BM боковой грани BCD.
Решение.
Пусть и MK — средняя линия
треугольника CDH. Тогда
следовательно,
, значит,
и,
. Кроме того,
.
Пусть длина ребра тетраэдра равна
, тогда имеем:
;
;
Ответ:
.
.
C2 В правильном тетраэдре ABCD найдите угол между медианой BM грани ABD и плоскостью BCD.
Решение.
Пусть, DN — высота грани BCD, O — центр треугольника BCD, MK — средняя линия треугольника ADO.
,
, значит,
Кроме
Далее имеем:
и, следовательно,
того,
— искомый.
,
откуда
;
.
Ответ:
.
C2 В правльной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла межд
плоскостью, проходящей через точку A перпендикулярно прямой BD.
Решение.
Пусть
точка O —
центр
плоскость SACперпендикулярна
точку Aперпендикулярно BD.
основания,
аM—
середина
ребра AS.
Поскольку
прямой BD. Это значит, что плоскость SAC и есть плоскость,
Проведем
Так
отрезки MD и MO.
равнобедренный,
как
треугольник SAD правильный,
Так
как
Следовательно, искомый угол равен углу OMD. Найдем стороны треугольник
.
По теореме косинусов:
.
Отсюда
.
Ответ:
.
Примечание.
Решение существенно упрощается, если заметить, что треугольник MOD — прямоугольный:
C2 В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые реб
угол между прямыми SB и CD.
Решение.
Вместо прямой CD рассмотрим параллельную ей прямую BE. Искомый угол равен углуSBE. Треугольник S
поскольку
большая
Следовательно,
Ответ:
диагональ
правильного
шестиугольника
вдвое
больше
его
сто
.
.
C2 № 484568. Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны ме
угол между прямой BM и плоскостью BDP, если точка M — середина бокового ребра пирамиды AP.
Решение.
Пусть отрезок PH — высота пирамиды PABCD, отрезок MN — средняя линия треугольника A
Поскольку PABCD —
правильная
пирамида,
точка H —
центр
квадрата ABCD,
значит,
откуда
. Но,
, следовательно,
. Таким образом, прямая BN — про
плоскость BDP, значит, угол мужду прямой BM и плоскостью BDP равен углу между прямой BM и прямо
углу MBN прямоугольного треугольника MBN.
Примем
длину
и, следовательно,
ребра
данной
пирамиды
за
,
Ответ:
.
1,
тогда
,
.
C2 Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Най
прямыми РН и ВМ, если отрезок РН — высота данной пирамиды, точка М — середина ее бокового ребра АР
Решение.
Пусть
отрезок MN —
средняя
линия
треугольника АРН,
параллельная
его
стороне Р
Поскольку PABCD — правильная пирамида, точка Н — центр квадрата ABCD. Так как
, а, значит,
. Прямые MN и РН параллельны, следовательно, угол между пря
углу между прямыми MN и ВМ, т. е. острому углу BMN прямоугольного треугольника ВМN.
Примем длину ребра данной пирамиды за 1, тогда
,
,
,
Ответ:
.
.
C2 В кубе
Решение.
все ребра равны 1. Найдите расстояние от точки С до прямой
Проведем отрезок
и опустим перпендикуляр СН на
.
Искомое расстояние равно высоте СН прямоугольного треугольника
с прямым углом С:
.
Ответ:
.
.
C2 Дан
куб
плоскости
Решение.
М—
.
Длина
ребра
куба
равна
1.
Найдите
расстояние
середин
.
середина
Значит,
,N—
середина
.
Проведем
. Поэтому точка Н лежит на отрезке
перпендикуляр NH из
точки N к
, перпендикулярном
Искомый отрезок NH является высотой прямоугольного треугольника
с прямым углом N.
.
.
плоскости
.
Поэтому
Ответ:
от
C2
C2 № 484572. Дана правильная четырёхугольная пирамида SABCD с вершиной S. Ребро ос
равно
, высота —
. Найдите расстояние от середины ребра AD до прямой МТ, где точк
ребер CS и ВС соответственно.
Решение.
Пусть О — центр основания, а N — середина ребра SD, Р — середина ребра AD. Тогда
точки Р, N, M, Т лежат в одной плоскости и являются вершинами трапеции.
По теореме о средней линии треугольника
, так что трапеция равноб
Так как
,
Основания
Тогда
трапеции
равны
,а
,
.
В
треугольнике РМТ проведем
,а
Заметим, что
.
, поэтому
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
Тип
C2
Условие
C2 № 484573. Дана правильная треугольная пирамида DABC с вершиной D. Боковое ребро пир
высота равна
. Найдите расстояние от середины бокового ребра BD до прямой МТ, где точк
ребер АС и AD соответственно.
Решение.
Пусть Р — середина ребра BD, Q — середина ребра ВС. По теореме о средней линии треугольн
следовательно, точки М, Т, Р, Q лежат в одной плоскости.
, следовательно, точки М, Т, Р, Q являются вершинами параллелограмма. Кр
а по теореме о трёх перпендикулярах
(так как
), поэтому
прямоугольник. Значит, искомое расстояние есть длина отрезка РТ. По теореме Пифагора
;
тогда
,а
Ответ: 3.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
.
этот
C2
C2 № 484574. Дана правильная треугольная пирамида DABC с вершиной D. Сторона основания п
, высота равна
. Найдите расстояние от середины бокового ребра BD до прямой МТ, где точк
ребер АС и AВ соответственно.
Решение.
Пусть Q — середина ребра CD, P — середина ребра ВD. По теореме о средней линии треугольни
следовательно, точки М, Т, Р, Q лежат в одной плоскости.
, следовательно, точки М, Т, Р, Q являются вершинами параллелограмма. Кр
а по теореме о трёх перпендикулярах (так как
искомое
расстояние
По теореме Пифагора
есть
), поэтому этот параллелограмм — пря
длина
отрезка РТ.
;а
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
Отрезок АО раве
.
C2
C2 № 484577. В правильной треугольной призме
между прямыми
Решение.
Так
как
и
прямая
параллельной
плоскости
.
пересекается
,
, все рёбра которой равны 1,
то
расстояние
с
прямой
между
параллельной
прямыми
и
прямой
равно
и
лежит
расстоянию
в
о
.
Пусть АК — высота треугольника ABC. АК перпендикулярна , так как перпендикулярна плоскости A
искомое расстояние — длина отрезка АК. Из равностороннего треугольника ABC находим:
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 485934. Основанием
прямой
призмы
является
равнобедренный
Высота призмы равна 3. Найдите угол между прямой
и плоскостью
Решение.
Поскольку
призма
плоскости
прямая,
Поэтому прямая
то
высота
— проекция прямой
на плоскость
углу
Так
Отсюда
как
имеем:
Следовательно,
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
треугольника
Значит,
C2
C2 № 485943. Основанием
гипотенузой
и
прямой
призмы
катетом
является
Высота
призмы
равна
прямоугольный
Найдите
угол
т
меж
плоскостью
Решение.
Поскольку
призма
прямая,
перпендикулярна плоскости
Поэтому прямая
искомый
угол
то
высота
— проекция прямой
тре
на плоск
равен
Так как
Рассмотрим
прямоугольный
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
тр
C2
C2 № 485968. Основание
котором
прямой
,
середину ребра
Решение.
четырехугольной
призмы
—
прямоуг
. Найдите угол между плоскостью основания призмы и плоскостью
перпендикулярно прямой
Расстояние между прямыми
высота
и
, если расстояние между прямыми
и
равно расстоянию между основаниями, то есть высо
призмы
равна
Угол между плоскостями равен углу между прямыми, перпендикулярными этим плоскостям. По
равен
Рассмотрим
углу
треугольник
Значит,
между
.
Его
ребром
катеты
равны
.
Ответ: 45 .
Спрятать решение
Ответы на вопросы (1)
Тип
Обсудить ВКонтакте
Сообщить об ошибке
Условие
и
,
C2
C2 № 485978. В правильной треугольной пирамиде SABC с основанием ABC точка M — середина
середина ребра SB. Найдите угол между плоскостями CMK и ABC, если SC = 6, BC = 4.
Решение.
Проведем перпендикуляр
основания.
Точка
плоскостей
и
лежит
к
— середина
на
медиане
и
Из точки
треугольника
Следовательно,
Далее находим:
Откудп
Поскольку
имеем:
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
опустим перпендикуля
параллельна
пря
—
уго
линейный
C2
C2 № 485981. Основание
котором
середину ребра
Решение.
,
прямой
четырехугольной
призмы
—
прямоуг
. Найдите угол между плоскостью основания призмы и плоскостью
перпендикулярно прямой
Расстояние между прямыми
высота
и
, если расстояние между прямыми
и
равно расстоянию между основаниями, то есть высо
призмы
равна
Угол между плоскостями равен углу между прямыми, перпендикулярными этим плоскостям. По
равен углу между ребром
и прямой
. Рассмотрим треугольник
Значит,
Ответ: 45
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
. Его катеты
C2
C2 № 485988. Дана правильная четырехугольная пирамида SABCD. Боковое ребро
равна 2. Найдите расстояние от точки B до плоскости ADM, где M — середина ребра SC.
Решение.
Построим сечение ADMK, где K — середина ребра SB. Прямая BCпараллельна AD, значит, искомо
расстоянию
до
точки N плоскости ADM, где N —
Пусть P — середина AD. Рассмотрим сечение NSP:
.
Значит,
треугольник SNP равносторонний.
Искомое
расстояние
равно
расстоянию
середина SN, PQ — медиана и высота треугольника SNP. Поэтому искомое расстояние рав
Ответ: 1.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 485992. Дана правильная четырехугольная пирамида
равна 2. Найдите расстояние от точки
Решение.
до плоскости
Боковое ребро
где
— середина ребра
Построим сечение ADMK, где K — середина ребра SB. Покажем, что искомое расстояние равно
середина
апофемы SN.
Действительно,
пусть P —
середина
стороны AD, AD перпе
поэтому AD перпендикулярна плоскости SNP, а тогда и KM — средняя линия боковой грани — пер
другой стороны,SQ перпендикулярна KM. Тогда SQ — перпендикуляр к плоскости сечения, его дл
расстоянию.
Рассмотрим сечение NSP. Имеем:
.
Значит,
треугольник SNP равносторонний.
Искомое
Ответ: 1.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
расстояние
равно SQ=
C2
C2 № 485997. Основание
котором
середину ребра
Решение.
прямой
четырехугольной
призмы
—
прямо
Найдите угол между плоскостью основания призмы и плоскостью
перпендикулярно прямой
если расстояние между прямыми
Расстояние между прямыми
есть высоте призмы. Значит, высота призмы равна
и
и
равно расстоянию меж
Угол между плоскостями равен угл
перпендикулярными этим плоскостям. Следовательно, искомый угол равен углу между ребром
Рассмотрим треугольник
Его катеты равны
По
Ответ: 60 .
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 486000. В правильной треугольной пирамиде
точка
— середина ребра
Решение.
Проведем перпендикуляр
основания. Точка
плоскостей
плоскостями.
Найдите угол между плоскостями
к
— середина
лежит на медиане
и
с основанием
и
Из точки
треугольника
Откуда
Ответ:
Спрятать решение
Тип
Сообщить об ошибке
Условие
— с
если
опустим перпендикуля
Прямая
Следовательно,
Далее находим:
Обсудить ВКонтакте
и
точка
параллельна п
— линейный угол и
C2
C2 № 500001. Основанием прямого параллелепипеда
является ромб ABCD
равна
а угол ВАD равен
. Найдите расстояние от точки А до прямой
ребро данного параллелепипеда равно 8.
Решение.
, если изв
Опустим из точки A перпендикуляр AE на прямую
грани
прямую EF, параллельную прямой
прямая AF является
следовательно,
проекцией
и
прямой AE на
согласно
. Так как
плоскость ABC.
, то и
Поскольку
теореме
о
Далее
1)
из
2) из
:
.
О т в е т : 10.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
и про
:
,
трех
C2
C2 № 500007. Основанием
прямой
призмы
является
сторона которого равна
а угол ACB равен
известно, что боковое ребро данной призмы равно 12.
Решение.
равнобедренный
. Найдите расстояние от точки А до п
Опустим из точки A перпендикуляр AE на прямую
грани
прямую EF, параллельную прямой
. Так как
согласно
теореме
, то
о
трех
Далее
1)
из
2) из
:
.
О т в е т : 15.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
и про
, то и
прямая AF является проекцией прямой AE на плоскость ABC. Поскольку
и
треугол
:
C2
C2 № 500024. В прямоугольном параллелепипеде
между прямой
Решение.
и плоскостью
.
Плоскости
плоскости
углу
,
лежит в плоскости
. В прямоугольном треугольнике
и
перпендикулярны.
и пересекает прямую
катет
Перпендикуляр
в точке E. Значит, и
, гипотенуза
.
Тогда
.
Ответ:
.
Примечание.
Возможны другие формы ответа:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
.П
C2
C2 № 500025. В прямоугольном параллелепипеде
между прямой
Решение.
и плоскостью
Плоскости
и
плоскости
и пересекает прямую
треугольнике
.
перпендикулярны.
с катетом
,
Перпендикуляр
из
точки
к
в точке E. Значит, искомый угол равен углу
и гипотенузой
имеем:
.
Следовательно,
Ответ:
.
Примечание.
Возможны другие формы записи ответа:
.
Спрятать решение
Обсудить ВКонтакте
Тип
плоскост
Сообщить об ошибке
Условие
C2
C2 № 500112. Точка
Решение.
Примем
Прямая
— середина ребра
ребро
параллельна
куба
куба
прямой
Из прямоугольного треугольника
,
. Найдите угол между пр
за
значит,
с прямым углом
единицу.
искомый
угол
равен
имеем:
,
тогда
Ответ
также
может
быть
представлен
в
следующем
виде:
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
или
C2
C2 № 500193. Точка
плоскостью
Решение.
—
середина
ребра
В
ребро
в
равнобедренном
высота
Поскольку
.
его
середине —
пересекает
точке
.
треугольнике
площа
.
— средняя линия треугольника
Обсудить ВКонтакте
прямую
—
в
сечение
точке
куба
,
, получаем:
Ответ: 4,5.
Спрятать решение
Тип
Найдите
, если ребра куба равны 2.
Прямая
пересекает
куба
Сообщить об ошибке
Условие
п
C2
C2 № 500213. На ребре
между прямыми
Решение.
куба
и
отмечена точка
.
Примем
Поскольку
Проведем
,
через
точку
треугольники
так, что
куба
за
единицу.
получаем:
прямую,
и
ребро
равны.
В прямоугольном треугольнике
В прямоугольном треугольнике
параллельную
Искомый
угол
.
Она
и
пересекает
равен
углу
ребро
(или
в
смеж
с прямым углом
с прямым углом
В треугольнике
откуда
, тогда
Ответ
может
быть
Ответ:
Спрятать решение
представлен
и
в
другом
виде:
.
Ответы на вопросы (1)
Обсудить ВКонтакте
Сообщить об ошибке
или
Тип
Условие
C2
C2 № 500347. В правильной треугольной призме
2, точка
— середина ребра
Решение.
стороны основания равны 1, бо
Найдите угол между плоскостями
Прямая
Плоскости
тогда
и
отрезок
пересекаются по прямой
(проекция
)
двугранного
угла,
Точка
середина
—
Из равенства треугольников
пересекает
. Из точки
перпендикулярен
и
прямую
опустим перпендикуляр
прямой
.
Угол
является
образованного
ребра
и
В равнобедренном треугольнике
откуда
плоскостя
,
поэтом
получаем:
угол
равен
,
высота
.
Из прямоугольного треугольника
с прямым углом
получаем:
, тогда
Ответ
может
Ответ:
Спрятать решение
быть
представлен
и
в
другой
форме:
.
явля
Тип
Условие
C2
C2 № 500387. На ребре
между прямыми
Решение.
куба
и
отмечена точка
.
Примем
Поскольку
Проведем
,
через
треугольники
так, что
точку
куба
за
единицу.
получаем:
прямую,
и
ребро
параллельную
равны.
В прямоугольном треугольнике
В прямоугольном треугольнике
Искомый
.
угол
Она
равен
и
пересекает
углу
ребро
в
(или
с прямым углом
с прямым углом
В треугольнике
откуда
, тогда
Ответ
может
быть
Ответ:
Спрятать решение
представлен
и
в
.
Обсудить ВКонтакте
Сообщить об ошибке
другом
виде:
или
смеж
Тип
Условие
C2
C2 № 500408. Точка
—
середина
ребра
куба
.
Найдите
угол
ме
и
.
Решение.
Примем ребро куба за единицу. Тогда
параллельную
углу
. Она пересекает продолжение ребра
(или
. Проведём чере
в точке
смежному
В прямоугольном треугольнике
В прямоугольном треугольнике
, причём
. И
с
с прямым углом
с прямым углом
В треугольнике
,
откуда
,
а тогда
.
Ответ:
.
Примечание.
Ответ может быть представлен и в другом виде:
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
Тип
Условие
C2
C2 № 500428. Точка
—
середина ребра
куба
. Найдите
угол
ме
и
.
Решение.
Примем ребро куба за единицу. Тогда
параллельную
углу
. Она пересекает продолжение ребра
(или
. Проведём чере
в точке
, причём
смежному
В прямоугольном треугольнике
В прямоугольном треугольнике
с
с прямым углом
с прямым углом
В треугольнике
откуда
а тогда
.
Ответ:
.
Примечание.
Ответ может быть представлен и в другом виде:
.
Спрятать решение
. И
Тип
C2
Условие
C2 № 500474. Точка
плоскостью
Решение.
—
середина
ребра
Прямая
пересекает
В
ребро
в
равнобедренном
высота
Поскольку
куба
.
его
середине —
пересекает
точке
.
треугольнике
.
— средняя линия треугольника
Обсудить ВКонтакте
прямую
—
сечение
в
площа
точке
куба
,
, получаем:
Ответ: 18.
Спрятать решение
Тип
Найдите
, если ребра куба равны 4.
Сообщить об ошибке
Условие
п
C2
C2 № 500588. В правильной четырёхугольной призме
рёбра
равны
.
плоскостями
Решение.
На
ребре
и
отмечена
точка
так,
пересекает
пересекаются
.
Найд
прямую
в
точке
.
по
Из точки
опустим перпендикуляр
прямой
. Угол
на прямую
, тогда отрезок
(проекция
является линейным углом двугранного угла, образованного плоскостям
Поскольку
, получаем:
Из подобия треугольников
В прямоугольном
откуда высота
что
.
Прямая
и
стороны основания р
треугольнике
и
находим:
с
прямым
углом
:
;
;
.
Из прямоугольного треугольника
с прямым углом
получаем:
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
Тип
Условие
C2
C2 № 500595. В правильной четырёхугольной призме
ребра
равны
.
плоскостями
Решение.
На
ребре
и
отмечена
точка
так,
пересекает
пересекаются
.
Найд
прямую
в
точке
.
по
Из точки
опустим перпендикуляр
прямой
. Угол
на прямую
, тогда отрезок
(проекция
является линейным углом двугранного угла, образованного плоскостям
Поскольку
, получаем:
Из подобия треугольников
В прямоугольном
откуда высота
что
.
Прямая
и
стороны основания р
треугольнике
и
находим:
с
прямым
углом
:
;
;
.
Из прямоугольного треугольника
с прямым углом
получаем:
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
Тип
C2
Условие
C2 № 500639. В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведе
середины ребер АВ и ВС и вершину S. Найдите площадь этого сечения, если все ребра пирамиды р
Решение.
Пусть M — середина AB, а N — середина BC. Тогда площ
треугольника SMN.
Найдем
последова
площади
SM и SN — медианы треугольников SAB и SBC соответственно. Т. к. эти треугольники равносторон
ребра пирамиды одинаковой длины),
.
Найдем теперь MN из прямоугольного треугольника MBN. В нем катеты равны 4. Гипотену
Пифагора,
будет
Теперь найдем площадь равнобедренного треугольника SMN. Для этого проведем высоту SH, по
равную
, и вычислим площадь:
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 500643. В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведе
середины рёбер АВ и ВС и вершину S. Найдите площадь этого сечения, если боковое ребро пи
сторона основания равна 4.
Решение.
площади
Пусть M — середина AB, а N — середина BC. Тогда площ
треугольника SMN.
Найдем
последова
SM и SN — медианы треугольников SAB и SBC соответственно. Т. к. эти треугольники равнобед
пирамида правильная),
Найдем теперь MN из прямоугольного треугольника MBN. В нем катеты равны 2. Гипотену
Пифагора,
будет
Теперь найдем площадь равнобедренного треугольника SMN. Для этого проведем высоту SH, к
Пифагора, равна
, и вычислим площадь:
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 500874. В правильной четырехугольной пирамиде
середины ребер
Решение.
и
и вершину
с основанием
прове
найдите площадь этого сечения, если все ребра пирами
Изобразим указанное в условии сечение — треугольник
Проведем
в
треугольнике
Значит,
Из треугольника
находим
Из треугольника
находим
Тогда
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
высоту
C2
C2 № 500898. В правильной четырехугольной пирамиде
середины ребер
Решение.
и
и вершину
с основанием
прове
найдите площадь этого сечения, если все ребра пирами
Изобразим указанное в условии сечение — треугольник
Проведем
в
треугольнике
Значит,
Из треугольника
находим
Из треугольника
находим
Тогда
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
высоту
C2
C2 № 500918. В правильной треугольной пирамиде
угол
равен 36°. На ребре
взята точка
сечения пирамиды, проходящего через точки
Решение.
,
Нужное
Рассмотрим треугольник
Значит,
так, что
сторона осн
— биссектриса угла
и
сечение
—
Он равнобедренный,
т
, поэтому
.
Рассмотрим
теперь
треугольник
Таким
с основанием
образом,
треугольник
.
равнобедренный,
и
треугольник
Сумма
его
углов
поэтому
равносторонний
,
значит,
Аналогично
со
стороной
8.
Его
находим
площадь
рав
Ответ:
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
Тип
C2
Условие
C2 № 500962. В правильной треугольной призме
4. Изобразите сечение, проходящее через вершины
Показать решение
Обсудить ВКонтакте
Тип
стороны основания равны 6, бо
и середину ребра
Сообщить об ошибке
Условие
. Найдите его пл
C2
C2 № 500968. В правильной треугольной призме
стороны основания равны
равны
. Изобразите сечение, проходящее через вершины
Решение.
и середину ребра
Обозначим
через
и
средины
ребер
. Най
и
По теореме о средней линии треугольника
так что прямые
и
лежат
Сечение про которое спрашивается в условии, − это сечение призмы этой плоскостью. Оно
равнобокую
т
Основания трапеции
по теореме Пифагора найдем боковую сторону:
Проведем в трапеции высоту
Отрезок
Следовательно, высота трапеции
равен полуразности оснований трапеции:
Зная её, находим площадь трапеции:
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 501045. В правильной четырёхугольной пирамиде SABCD точка S — вершина. Точка M —
точка K — середина ребра SC. Найдите угол между плоскостями BMK и ABC, если AB=8, SC=10.
Решение.
Проведем из точки
Прямая
перпендикуляр
параллельна
Следовательно,
—
прямой
и
прямой
искомый
— середина MK. Точка Q является сере
пересечения
плоскостей
линейный
Значит,
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
и
угол.
C2
C2 № 501124. В правильной треугольной призме ABCA'B'C' стороны основания равны 6, а боко
Изобразите сечение, проходящее через вершины A, B и середину ребра A'C'. Найдите его площадь
Решение.
Параллельные грани оснований сечение пересекает по параллельны
сечение
—
трапеция.
Пусть
точка М —
середина A'C',
точка N —
серединаB'С'.
трапеции ABNM являются гипотенузами равных прямоугольных треугольников AA'M и BB'N, катеты
4.
Тем
самым,
трапеция
является
равнобедренной,
а
ее
боковые
стор
Отрезок MN — средняя линия треугольника A'B'C', поэтому MN = 0,5A'C' = 3. Пусть MK— высота тр
Следовательно,
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 501125. В правильной шестиугольный призме ABCDEFA'B'C'D'E'F' все ребра равны 1. Н
прямой AC' и плоскостью ACD'.
Решение.
Введем прямоугольную систему координат, как показано на рису
координат:
откуда
Плоскость
точек
Не
и
теряя
проходит через начало координат, ее уравнение имеет вид
имеем систему уравнений:
общности,
положим
тогда
вектор нормали к ней
Уравнение
Тогда искомый угол между прямой
плоскости
:
и плоскостью
Ответ:
Приведем
другое
—
так
искомый,
как
так
в
как
это
силу
угол
между
того,
прямой
и
е
что
Рассмотрим
(т.
к.
—
диагональ
к
Тип
C2
Условие
C2 № 501216. Расстояние между боковыми ребрами AA1 и BB1 прямой треугольной призмы AB
расстояние между боковыми ребрами AA1 и СС1 равно 8. Найдите расстояние от прямой AA1 до п
известно, что двугранный угол при ребре AA1 равен 60°.
Решение.
следовательно, расстояние
ребрами AA1 и СС1 равно AC.
Поскольку ABCA1B1C1 ― прямая призма, ее боковые грани
между боковыми ребрами AA1 и BB1 равно AB, а расстояние
Кроме того, уголBAC ― линейный угол двугранного угла
Таким
образом,
Пусть отрезок AH ― высота основания ABC (см. рисунок). Поскольку
и
и, значит, длина отрезка AHи есть искомое расстояние от прямой AA1 до параллельной
Рассматривая
треугольник ABC,
1.
2.
3.
Ответ:
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
C2
C2 № 501396. Длины ребер AB, AA1 и AD прямоугольного параллелепипеда ABCDA1B1C1D1 равны
16 и 15. Найдите расстояние от вершины A1 до прямой BD1.
Решение.
Опустим
как
то
откуда
из
точки
а, значит, отрезок
перпендикуляр
на
― высота прямоугольного тре
Далее
Ответ: 12.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
Тип
C2
Условие
C2 № 501416. Длины ребер BC, BB1 и BA прямоугольного параллелепипеда ABCDA1B1C1D1 равны
12 и 9. Найдите расстояние от вершины D1 до прямой A1C.
Решение.
Опустим из точки D1 перпендикуляр D1E на прямую A1C. Так как
то
а,
откуда
значит,
отрезок D1E ―
Далее находим:
Ответ:
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
высота
прямоугольного
Тип
C2
Условие
C2 № 501436. В правильной треугольной призме
равно . Точка
Решение.
Пусть
— середина ребра
— высота треугольника
. Тогда
поскольку в правильной призме
пирамида с вершиной в точке
Площадь основания равна
боковое ребро равно
. Найдите объём пятигранника
и основанием
по признаку перпендикулярности
и, значит,
Тип
. Пятигранник
— прямоугольной трапецией. Высота пир
Ответ: 3.
Спрятать решение
Обсудить ВКонтакте
,
.
Сообщить об ошибке
Условие
C2
C2 № 501456. В правильной треугольной призме
равно . Точка
Решение.
Пусть
-
— середина ребра
высота
боковое ребро равно
. Найдите объём пятигранника
треугольника
тогда
по
плоскости, поскольку в правильной призме
четырёхугольная
пирамида
Высота пирамиды
с
вершиной
в
и
основанием
Площадь основания равна
Ответ: 6
Спрятать решение
Обсудить ВКонтакте
Тип
признаку
перпендикул
и, значит,
точке
Сообщить об ошибке
Условие
,
.
Пятигра
-
прямоуго
C2
C2 № 500132. В правильной четырёхугольной призме
рёбра
равны
3.
плоскостями
Решение.
На
ребре
и
отмечена
стороны основания р
точка
так,
что
.
Найд
.
Прямая
пересекает прямую
пересекаются
в точке
. Плоско
по
Из точки
опустим перпендикуляр
прямой
. Угол
на прямую
, тогда отрезок
(проекция
является линейным углом двугранного угла, образованного плоскостям
Поскольку
, получаем:
Из подобия треугольников
В прямоугольном
откуда высота
и
треугольнике
находим:
с
прямым
углом
:
;
;
.
Из прямоугольного треугольника
с прямым углом
получаем:
.
Ответ
может
быть
представлен
и
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
в
другой
форме:
или
Тип
C2
Условие
C2 № 500448. В правильной шестиугольной призме
расстояние от точки
Решение.
до плоскости
Прямые
прямую
и
, перпендикулярна плоскости
треугольника
, в котором
все рёбра
.
перпендикулярны прямой
,
,
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
. Плоскость
. Значит, искомое расстояние равно высоте
Сообщить об ошибке
Условие
:
C2
C2 № 500468. В правильной шестиугольной призме
расстояние от точки
Решение.
до плоскости
.
Прямые
прямую
и
, перпендикулярна плоскости
треугольника
, в котором
все рёбра
перпендикулярны прямой
. Значит, искомое расстояние равно высоте
,
,
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
. Плоскость
Сообщить об ошибке
Условие
:
C2
C2 № 484566. В
правильной
шестиугольной
призме
все
равны 1найдите расстояние от точки B до прямой
Решение.
Проведем
отрезки BF и
.
,
поскольку
а
плоскость основания. По теореме о трех перпендикулярах
отрезка
Таким образом искмое
.
Рассмотрим
треугольник
.
Он
прямоугольный,
По теореме Пифагора находим:
.
Ответ: 2.
Спрятать решение
Ответы на вопросы (1)
Тип
. BF —
Обсудить ВКонтакте
Сообщить об ошибке
Условие
C2
C2 № 485966. В правильной четырехугольной призме
равна
. Точка
Решение.
Рассмотрим
— середина ребра
треугольную
высота равна 1, а
. Найдите расстояние от точки
пирамиду
.
Ее
объем
до плоскости
можно
выразить
д
1)
.
2)
,
Приравняем выражения для объемов и выразим его:
где
искомое
Найдем площадь равнобедренного треугольника
. Проведем в нем высоту
.
.
.
.
.
.
Следовательно,
искомое
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
расс
Тип
C2
Условие
C2 № 500019. В правильной шестиугольной призме
расстояние от точки В до плоскости
Решение.
Прямые
прямую EF,
перпендикулярна
треугольника
и FB перпендикулярны
плоскости
, в котором
все рёбра
.
прямой EF.
, значит искомое
,
,
расстояние
. Поэтому
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
Плоскость
равно
высоте
C2
C2 № 500367. В правильной четырёхугольной призме
рёбра
равны
3.
плоскостями
Решение.
На
ребре
и
отмечена
стороны основания р
точка
так,
что
.
Прямая
пересекает прямую
пересекаются
в точке
. Плоско
по
Из точки
опустим перпендикуляр
прямой
. Угол
на прямую
, тогда отрезок
(проекция
является линейным углом двугранного угла, образованного плоскостям
Поскольку
, получаем:
Из подобия треугольников
В прямоугольном
откуда высота
и
находим:
треугольнике
с
прямым
углом
:
;
;
.
Из прямоугольного треугольника
с прямым углом
получаем:
.
Ответ
может
быть
представлен
и
в
другой
форме:
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Найд
.
Сообщить об ошибке
Условие
или
C2
C2 № 484575. В правильной шестиугольной призме
стороны основ
3, а боковые ребра равны 4, найдите расстояние от точки С до прямой
Решение.
.
Так как ABCDEF правильный шестиугольник, то прямые FC и DE параллельны, параллельны также
следовательно, прямые
прямыми
и FC параллельны. Расстояние от точки С до прямой
и FC.
В трапеции
:
,
,
,
тогда
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
, равно
C2
C2 № 484576. В правильной шестиугольной призме
стороны основ
4, а боковые ребра равны 3, найдите расстояние от точки В до прямой
Решение.
.
Так как ABCDEF правильный шестиугольник, то прямые BE и CD параллельны, параллельны та
и
,
следовательно,
прямые
расстоянию между прямыми
В трапеции
и
и
параллельны.
Расстояние
.
:
,
,
,
тогда
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
Сообщить об ошибке
Условие
от
точки B до
пр
C2
C2 № 485941. В правильной шестиугольной призме
найдите расстояние от точки
Решение.
Так
как
прямые
—
и
до прямой
правильный
.
шестиугольник,
, и следовательно, прямые
равно
расстоянию
В трапеции
:
,
, все рёбра
и
то
прямые
и
параллельны.
параллельны. Расстояние от точки
между
,
пря
Значит,
,
тогда
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Тип
П
Сообщить об ошибке
Условие
C2
C2 № 485955. В правильной шестиугольной призме
найдите расстояние от точки
Решение.
Так как
и
все рёбра
до прямой
— правильный шестиугольник, прямые
параллельны,
перпендикулярна
перпендикулярно
,
По условию
поэтому
Тогда
длина
и
по
перпендикулярны. Поск
теореме
отрезка
трёх
равна
диагональ правильного шестиугольника
треугольника
о
пер
искомому
. Тогда по теор
находим,
Ответ: 20.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
Тип
C2
Условие
C2 № 485962. В правильной шестиугольной призме
найдите расстояние от точки
Решение.
Так как
и
, все рёбра
до прямой
— правильный шестиугольник, то прямые
параллельны,
перпендикулярна
перпендикулярна
,
поэтому
.
длина
Тогда
и
по
отрезка
перпендикулярны. Пос
теореме
равна
о
трёх
пер
искомому
Далее имеем: меньшая диагональ правильного шестиугольника, сторона которого равна 10,
ребро
.
по условию, откуда по теореме Пифагора для треугольника
О т в е т : 20.
Спрятать решение
Обсудить ВКонтакте
Сообщить об ошибке
искомое рас
Тип
C2
Условие
C2 № 500013. В правильной шестиугольной призме
расстояние от точки В до плоскости
Решение.
Прямые
и DB перпендикулярны
прямую ED, перпендикулярна плоскости
треугольника
, в котором
все рёбра
.
прямой ED.
,
,
. Тогда
.
Ответ:
.
Спрятать решение
Обсудить ВКонтакте
Плоскость
. Значит, искомое расстояние равно высоте
Сообщить об ошибке