Угол между плоскостями в пространстве. Определение1. Определение 2.
advertisement
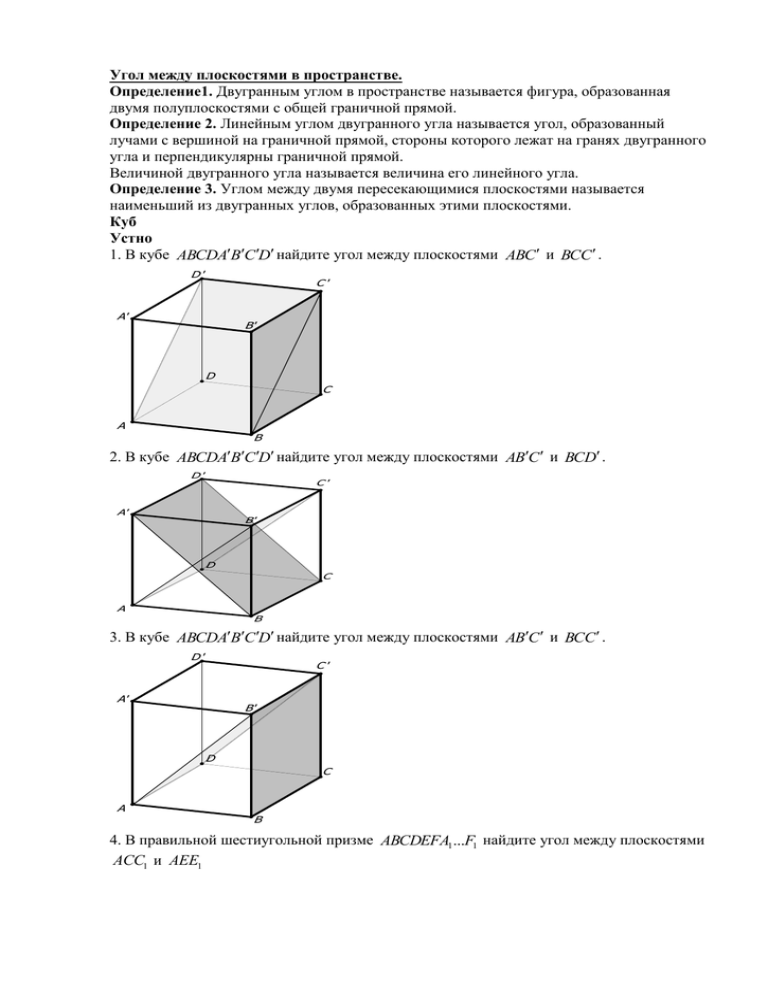
Угол между плоскостями в пространстве. Определение1. Двугранным углом в пространстве называется фигура, образованная двумя полуплоскостями с общей граничной прямой. Определение 2. Линейным углом двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой. Величиной двугранного угла называется величина его линейного угла. Определение 3. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями. Куб Устно 1. В кубе ABCDABC D найдите угол между плоскостями ABC и BCC . D' C' A' B' D C A B 2. В кубе ABCDABC D найдите угол между плоскостями ABC и BCD . D' C' A' B' D C A B 3. В кубе ABCDABC D найдите угол между плоскостями ABC и BCС . D' C' A' B' D C A B 4. В правильной шестиугольной призме ABCDEFA1 ...F1 найдите угол между плоскостями ACC1 и AEE1 E1 D1 C1 F1 A1 B1 E D C F A B Работа в тетради 1.В кубе ABCDABC D найдите тангенс угла между плоскостями ABC и BDC . D' C' A' B' D C A B Решение. D' Искомый угол C OC . Объясните почему? CC 1 tgC OC 2. OC 2 2 C' A' B' D C О A B Далее три задачи разбираем устно, рисуя линейные углы на чертежах. 2. В кубе ABCDABC D найдите тангенс угла между плоскостями АВС и CBD . D' A' C' B' D A C B 3. В кубе ABCDABC D найдите тангенс угла между плоскостями BCC и CBD . D' A' C' B' D A C B 4. В кубе ABCDABC D найдите тангенс угла между плоскостями ADD и BDC . D' A' C' B' D A C B Ответы: 2 ; 2 ; 2 . Почему ответы в этих трех задачах одинаковые. Далее, работа в тетради. 5.В кубе ABCDABC D найдите тангенс угла между плоскостями ABC и AB D . D' C' 2 Ответ: . A' 2 B' D A C B 6.В кубе ABCDABC D найдите косинус угла между плоскостями BD A и BDC . D' A' C' B' D A Решение. C B D' C' A' B' D C О A B A0 DB , C O DB . Каково положение точки О? Рассматриваем AC O . Находим все стороны этого треугольника. По теореме косинусов по трем сторонам находим cos AOC . 1 Ответ: 3 7. В кубе ABCDABC D точки E и F - середины ребер соответственно AB и AD . Найдите тангенс угла между плоскостями AEF и BCC . D' C' F A' B' E D C A B Решение. D' C' F A' B' E H D Прокомментируйте чертеж. Искомый угол? Какой EAH ? Вычислите искомый угол? 5 Ответ: 2 C A B Домашнее задание: 1. В кубе ABCDABC D найдите косинус угла между плоскостями BAC и AB D . 1 D' C' Ответ: 3 A' B' D A 2. C B В кубе ABCDABC D найдите угол между плоскостями BCD и ACC . D' C' A' Ответ: 60 B' D C A B 3. В кубе ABCDABC D точки E и F - середины ребер соответственно AB и AD . 2 Найдите тангенс угла между плоскостями AEF и BD D . Ответ: 4 Призмы Устно 1. В правильной шестиугольной призме ABCDEFA1 ...F1 найдите угол между плоскостями ABB1 и AEE1 E1 D1 C1 F1 A1 B1 E D C F B A 2. В правильной шестиугольной призме ABCDEFA1 ...F1 найдите угол между плоскостями AFF1 и BDD1 E1 D1 C1 F1 A1 B1 E D C F A B 3. В правильной шестиугольной призме ABCDEFA1 ...F1 найдите угол между плоскостями ABC и BDE1 E1 D1 C1 F1 A1 B1 E D F C A B 4. В правильной шестиугольной призме ABCDEFA1 ...F1 найдите угол между плоскостями ACC1 и BFF1 E1 D1 C1 F1 A1 B1 E D F C A B Работа в тетради 1. В правильной треугольной призме ABCABC , все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и BCA . Покажите линейный угол двугранного угла. Сделайте чертеж. В каком прямоугольном треугольнике работаем? Проведите необходимые вычисления. 2 3 Ответ: . 3 2. В правильной треугольной призме ABCABC , все ребра которой равны 1, найдите косинус угла между плоскостями BCA и ABC . Решение. B' C' Искомый угол APA . 1 Ответ: 7 A' Р B C A 3. В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и AEF1 . D1 E1 C1 F1 A1 E B1 D C F B A Решение. D1 E1 C1 F1 A1 E F B1 D Искомый угол FHF1 . Как получена точка H? Как найти отрезок FH ? 1 Объясните, почему FH . 2 Ответ: 2 C H A B 4. В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите угол между плоскостями ABC и BFE1 . Решение. E1 D1 Почему линейным углом данного C1 двугранного угла есть угол E1 FE ? F1 Докажите. A1 B1 Ответ45 E D C F A B 5. В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите угол между плоскостями AFD1 и CDF1 . Решение. E1 D1 Почему искомый угол ANA1 ? C1 Как найти отрезок A1 N ? F1 Почему A1C 2 ? M Почему ANA1 - равносторонний? E D B A1 1 Ответ:60 N C F A B 6.В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите косинус угла между плоскостями AFE1 и CDE1 . Постройте линейный угол двугранного D1 E1 угла и решите самостоятельно. 1 Ответ: F1 C1 7 B1 D A1 E C F A B 7.В правильной четырехугольной призме ABCDA1 B1C1 D1 стороны основания равны 1, а боковые ребра равны 4. На ребре AA1 отмечена точка E так, что AE : EA1 3 : 1 . Найдите угол между плоскостями ABC и BED1 . D' C' A' B' E D C A Решение. B D' AE 3, EA1 1 Из подобия треугольников A1 D1 E и AKE находим AK 3 . C' A' BK 12 32 10 3 10 AH 10 AE tgAHE 10 AH Ответ: arctg 10 B' E D C A B H K Домашнее задание. 1.Сторона основания правильной треугольной призмы ABCA1 B1C1 равна 2, а диагональ боковой грани равна 5 . Найдите угол между плоскостью A1 BC и плоскостью основания призмы. Ответ: 300 2.В правильной треугольной призме ABCA1 B1C1 стороны основания равны 1, боковые ребра равны 2, точка D - середина ребра CC1 . Найдите угол между плоскостями ABC и ADB1 . Ответ: arctg 2 3. В правильной четырехугольной призме ABCDA1 B1C1 D1 стороны основания равны 3, а боковые ребра равны 4. На ребре AA1 отмечена точка E так, что AE : EA1 1 : 3 . Найдите 10 3 4.В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точки D, E середины ребер соответственно A1 B1 и A1C1 . Найдите тангенс угла между плоскостями угол между плоскостями ABC и BED1 . Ответ: arctg ADE и BCC1 Ответ: 3 4 Пирамида. Устно 1. В правильном тетраэдре ABCD точка E - середина ребра AD . Найдите угол между плоскостями ACD и BCE .(900) D E C A B 2.В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, точка E середина SC . Найдите угол между плоскостями ABC и BDE . (300) S E D C A B 3. В правильной шестиугольной пирамиде SABCDEF найдите угол между плоскостями SAD и SBE (300) S D E C F B A 4. В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите угол между плоскостями BCE1 и BCC1 .(600) E1 D1 C1 F1 A1 E B1 D C F A B Работа в тетради 1.В тетраэдре ABCD , все ребра которого равны 1, найдите косинус угла между плоскостями ABC и ACD . D C B A Решение. Каково положение точки H ? Искомый угол DHD1 . Рассматриваем прямоугольный треугольник DHD1 . 1 Ответ: 3 D H B C D1 A 2. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите косинус угла между плоскостями ABC и SCD . S D C A B Решение. Продолжите решение. 3 Ответ: . 3 S H D C O A B 3. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите косинус угла между плоскостями SAB и SCD . S D A Решение. C B S Искомый угол MSH . Используем теорему косинусов в MSH . 1 Ответ: 3 H C D O B M A 4. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите тангенс угла между плоскостями SAС и SBC . S D C A B 5.В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите косинус двугранного угла, образованного гранями SAD и SCD . S D A Решение. C B Искомый угол AHC . Как его будем искать? S Ответы к задачам 4 и 5: 1 2и . 3 H C D B A 6.В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями ABC и SEF . S D E C F B A Решение. S D E H C F O A 2. B Рассмотрим SFE Как построили точку H ? Искомый угол SHO . 1. Рассматриваем FOE . Он равносторонний. Почему? OH - высота в равностороннем треугольнике со 3 стороной 1. Значит, OH . Почему? 2 Распишите подробнее. Тогда по теореме Пифагора в FSH : S 2 1 15 1 SH 2 2 4 . 4 2 2 F 3. cos SHO 2 2 HO 3 2 1 5 . SH 2 5 15 5 E 1 H 2 1 2 7. В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями SAF и SCD . S D E C F B A Решение. Искомый угол HSP . Найдем его по теореме косинусов из треугольника HSP . Чему равен отрезок HP ? Почему можно рассмотреть ABC ? Ответ: 0,6 S D E P F C H A B 8.В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями SAB и SAF . S Ответ: -0,6 D E C F A B 9.В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями SBD и SDF . S 5 Ответ: 13 D E C F A B Домашнее задание. 1.В правильной четырехугольной пирамиде SABCD с основанием ABCD сторона основания равна 6 2 , а боковое ребро равно 10. Найдите угол между плоскостями ABC и 8 ACM , где точка M делит ребро BS так, что BM : MS 2 : 1 Ответ: arctg 3 2.Основанием прямой треугольной призмы ABCA1 B1C1 является треугольник ABC , в котором AC BC 6 , а один из углов равен 600. На ребре CC1 отмечена точка P так, что CP : PC1 2 : 1. Найдите тангенс угла между плоскостями ABC и ABP , если расстояние между прямыми AC и A1 B1 равно 18 3 . Ответ:4 3.В прямоугольном параллелепипеде ABCDA1 B1C1 D1 известны ребра AB 8, AD 6, CC1 5 . Найдите угол между плоскостями BDD1 и AD1 B1 .Ответ: arctg 24 25 Метод координат 1. Нахождение угла между нормалями данных плоскостей. Задачу о нахождении угла между плоскостями и , заданными уравнениями a1 x b1 y c1 z d1 0 и a2 x b2 y c2 z d 2 0 соответственно, удобнее свести к задаче о нахождении угла между векторами их нормалей n a1 ; b1 ; c1 и n a 2 ; b2 ; c 2 , используя n n формулу cos ; n n Пример 1.В кубе ABCDA1 B1C1 D1 найти угол между плоскостями AB1C и BC1 D . X Z D' C' A' B' D C A B Y A0;0;0; B0;1;0 ; C1;1;0 ; D1;0;0 ; B1 0;1;1 ; C1 1;1;1 : ax by cz d 0 ; ax by cz d 0 d 0, b d 0, d 0, b d , a b d 0, a b, a d 0, a d , b c d 0 c b a b c d 0 c d :x yz 0 : x y z 1 0 n 1;1;1 n 1;1;1 111 1 1 ; Ответ: arccos 3 3 3 3 2. В правильной пирамиде MABCD (М – вершина) высота и сторона основания равны 4. Точка F - середина ребра MC . Плоскость проходит через середину ребра AM перпендикулярно прямой BF . Найти угол между: а) плоскостью и плоскостью основания; б) плоскостью и прямой DM . cos Z X M F D C A O Y B Решение. Так как BF , то BF - нормаль к плоскости , OM - нормаль к плоскости ABC . BF OM BF DM cos , ABC ; sin , DM BF OM BF DM O0;0;0 M 0;0;4 OM 0;0;4 B 2;2;0 D2;2;0 F 1;1;2 DM 2;2;4 BF 3;1;2 BF OM 24 2 cos , ABC 14 4 14 BF OM BF DM 3 2 1 2 2 4 sin , DM 0 14 2 6 BF DM Ответ: arccos 2 ;0 14 3. В единичном кубе ABCDA1 B1C1 D1 найти угол между плоскостями AD1 E и D1 FC , где точки E и F - середины ребер A1 B1 и B1C1 соответственно. Z D' C' A' B' X F E D C A B Y 1 1 A0;0;0; D1 1;0;1 ; E 0; ;1 ; F ;1;1 ; D1 1;0;1 ; C1;1;0 2 2 AED1 : ax by cz d 0 D1 FC : ax by cz d d 0, a c d 0, d 0, 1 1 b c d 0, a c, abcd 0 2 2 b 2c a c d 0 abd 0 cx 2cy cz 0 2bx by bz 3b 0 x 2y z 0 2x y z 3 0 n1 1;2;1 n2 2;1;1 0 c b, a 2b, d 3b 2 2 1 3 1 ; 60 0 ; Ответ: 600 6 2 6 6 4.Дан куб ABCDA1 B1C1 D1 . Найти угол между плоскостями MNP и AKD , где точки M центр грани AA1 B1 B , N - середина ребра B1C1 , K - середина ребра CC1 , точка P - делит ребро DD1 в отношении DP : PD1 1 : 2 . cos Z D' C' N A' B' K P M A X D C B Y Проведите решение самостоятельно. 125 125 ; Ответ: arccos MNP : n1 2;7;9; AKD : n2 0;1;2; cos 134 134 Подготовка к самостоятельной работе 1.В правильной четырехугольной призме ABCDA1 B1C1 D1 стороны основания равны 1, а боковые ребра равны 4. На ребре AA1 отмечена точка E так, что AE : EA1 3 : 1 . Найдите угол между плоскостями ABC и BED1 .Ответ: arctg 10 . 2.В правильной треугольной пирамиде SABCD сторона основания AB 2 , а боковое ребро SA 3 . Найдите угол между плоскостями SBC и SAD . Ответ: 900 3.Основание пирамиды DABC - равнобедренный треугольник ABC , в котором AB BC 13, AC 24. Ребро DB перпендикулярно плоскости основания и равно 20. Найдите тангенс двугранного угла при ребре AC .Ответ: 4 Самостоятельная работа по данной теме. Вариант 1 В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите косинус угла между плоскостями ACB1 и BA1C1 . C1 B1 A1 C B A Вариант 2 В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и CA1 B1 . C1 B1 A1 C B A Вариант 3 В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и DB1 F1 E1 D1 C1 F1 B1 A1 E D C F A B Вариант 4 В кубе ABCDA1 B1C1 D1 найдите тангенс угла между плоскостями ABC и DA1C1 D' C' A' B' D C A B Вариант 5 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, точка E середина ребра SC . Найдите угол между плоскостями ABC и BDE S E D C A B Вариант 6 В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и DB1 F1 E1 D1 C1 F1 A1 B1 E D C F A Ответы: 1. B 2 3 1 2 2. 3. 4. 7 3 3 2 5. 45 0 6.