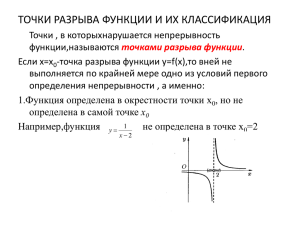
Примеры точек разрыва

Определение точек разрыва
Пример 3.3 Рассмотрим функцию
Функция имеет разрывы при
, для которой
и при
. Нетрудно видеть, что при
функция имеет неустранимые разрывы первого рода. В точке
(значения на краях разыва существуют, но не совпадают); в точке
В точках
имеем:
--
(снова пределы слева и справа существуют, но не совпадают).
Рис.3.5.График функции
Пример 3.4 Функция
при
и
имеет при
при
разрыв второго рода, так как
.
и
Рис.3.6.График функции
Пример 3.5 Функция
при
имеет при
и
разрыв второго рода, так как
.
Рис.3.7.График функции
Пример 3.6 Возьмём
. Все точки области определения
этой элементарной функции являются точками непрерывности.
Поскольку
не входит в область определения функции
, но
определена во
всех точках любой проколотой окрестности 0, то 0 -- точка разрыва функции
.
Разобранный выше пример 3.2 показывает, что если доопределить эту функцию при
, положив
, то функция становится непрерывной в точке 0. Значит, 0 --
точка разрыва первого рода для функции
.
Рис.3.8.Устранимый разрыв функции
Пример 3.7 Рассмотрим функцию
. Её область определения
состоит из точек непрерывности, так как это элементарная функция.
Точка
, в которой функция не определена, -- это точка разрыва функции.
Поскольку
при
, то
. Это означает, что при
функция имеет устранимый разрыв и становится непрерывной на всей
вещественной оси, если положить
.
Рис.3.9.Устранимый разрыв функции
Пример 3.8 Рассмотрим функцию
разрыв, так как
, то
, где
. Поскольку
. При
она имеет
-- ограниченная функция, а
при
(по теореме 2.7). Следовательно, разрыв устранимый, и если
доопределить функцию, положив
, она становится непрерывной при всех
.
Рис.3.10.График функции
при
Пример 3.9 Рассмотрим функцию
При
,
, заданную равенством
, так что последовательность
,
-- это геометрическая прогрессия со знаменателем
,и
При
что
имеет вид
При
,
,
,
,
Эта последовательность предела не имеет, так что функция
,
, и все
,
, так
, и последовательность
не определена при
.
Рис.3.11.График функции
Получаем, что
. Точками разрыва этой функции
служат как все точки, не принадлежащие области определения (точки вида
,
), так и все точки вида
,
, в которых функция принимает значение 1.
Все точки разрыва -- устранимые, так как пределы функции слева и справа в этих точках
совпадают и равны 0.
Пример 3.10 Рассмотрим функцию
, и точка
-- точка разрыва. Рассмотрим поведение функции слева и
справа от точки разрыва. При
будет
; её область определения
будет
и
не существует, и разрыв функции
и
; при
. Итак, значения "на правом берегу" разрыва
в точке
-- второго рода.
Рис.3.12.График функции
Замечание 3.1 Если функция
точке
слева или справа, то точку
не определена на интервале, примыкающем к
мы не считаем точкой разрыва функции.
Пример 3.11 Рассмотрим функцию
. При
стремится к 0 и положителен, так что
мы не считаем точками разрыва, так как функция
при
.
. Её область определения -и при
знаменатель
. однако точки
не определена при
и
и
Рис.3.13.График функции
Пример 3.12 Рассмотрим функцию
. Точка
несмотря на характер её поведения при
при
.
Рис.3.14.График функции
. Её область определения -- это
не является точкой разрыва функции
, поскольку функция
,
не определена