Зверькова К. Слонова Л.А. СФУx

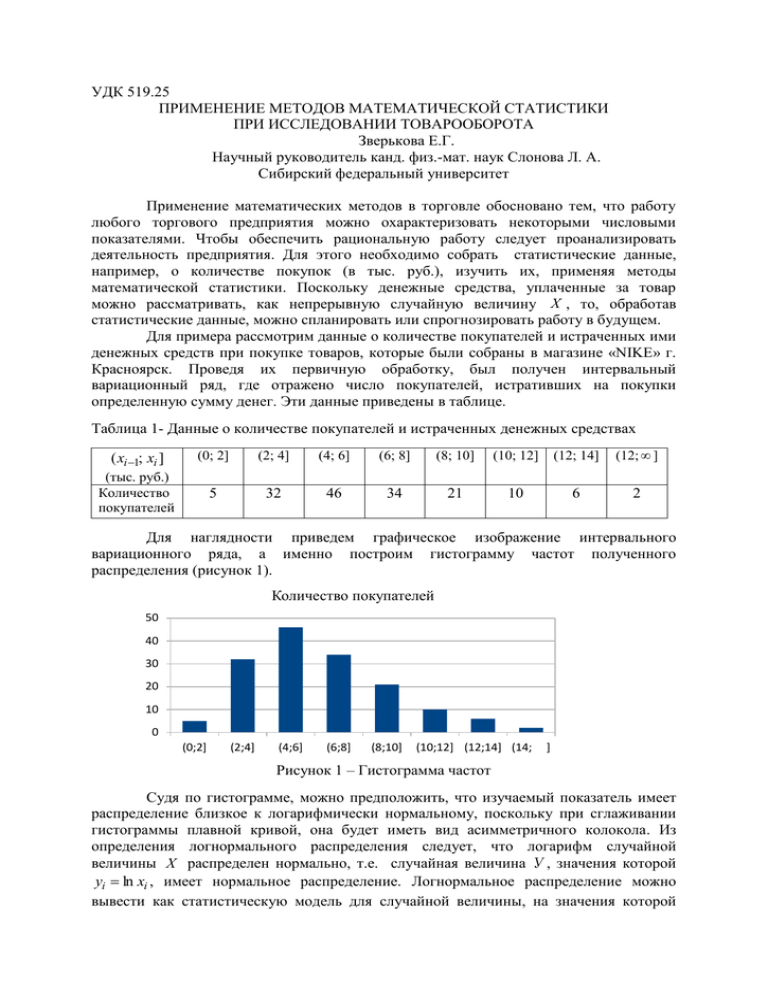
УДК 519.25
ПРИМЕНЕНИЕ МЕТОДОВ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ПРИ ИССЛЕДОВАНИИ ТОВАРООБОРОТА
Зверькова Е.Г.
Научный руководитель канд. физ.-мат. наук Слонова Л. А.
Сибирский федеральный университет
Применение математических методов в торговле обосновано тем, что работу
любого торгового предприятия можно охарактеризовать некоторыми числовыми
показателями. Чтобы обеспечить рациональную работу следует проанализировать
деятельность предприятия. Для этого необходимо собрать статистические данные,
например, о количестве покупок (в тыс. руб.), изучить их, применяя методы
математической статистики. Поскольку денежные средства, уплаченные за товар
можно рассматривать, как непрерывную случайную величину Х , то, обработав
статистические данные, можно спланировать или спрогнозировать работу в будущем.
Для примера рассмотрим данные о количестве покупателей и истраченных ими
денежных средств при покупке товаров, которые были собраны в магазине «NIKE» г.
Красноярск. Проведя их первичную обработку, был получен интервальный
вариационный ряд, где отражено число покупателей, истративших на покупки
определенную сумму денег. Эти данные приведены в таблице.
Таблица 1- Данные о количестве покупателей и истраченных денежных средствах
( xi 1; xi ]
(0; 2]
(2; 4]
(4; 6]
(6; 8]
(8; 10]
(10; 12]
(12; 14]
(12;  ]
(тыс. руб.)
Количество
покупателей
5
32
46
34
21
10
6
2
Для наглядности приведем графическое изображение интервального
вариационного ряда, а именно построим гистограмму частот полученного
распределения (рисунок 1).
Количество покупателей
50
40
30
20
10
0
(0;2]
(2;4]
(4;6]
(6;8]
(8;10]
(10;12] (12;14] (14;
]
Рисунок 1 – Гистограмма частот
Судя по гистограмме, можно предположить, что изучаемый показатель имеет
распределение близкое к логарифмически нормальному, поскольку при сглаживании
гистограммы плавной кривой, она будет иметь вид асимметричного колокола. Из
определения логнормального распределения следует, что логарифм случайной
величины Х распределен нормально, т.е. случайная величина У , значения которой
yi  ln xi , имеет нормальное распределение. Логнормальное распределение можно
вывести как статистическую модель для случайной величины, на значения которой
влияет много неучтенных факторов. Например, в данном случае могут быть
следующие: качество товара, расположение магазина, его посещаемость, предпочтение
покупателей и др. Вклад этих факторов в общую сумму достаточно мал, и их влияние
скорее мультипликативно, чем аддитивно. С помощью центральной предельной
теоремы теории вероятностей можно показать, что распределение произведения
независимых положительных случайных величин приближается к логарифмически
нормальному распределению.
Функция плотности логнормального распределения имеет вид:
f ( x) 
1 1
e
 2 х

(ln x  a ) 2
2 2
,
(1)
при x  0 . Параметры a  M (ln X )  M (Y ) и  2  D(ln X )  D(Y ) , где Y  ln X .
Чтобы найти оценки этих параметров, при наличии интервального
вариационного ряда, воспользуемся формулами:
k
k
1 k
(2)
а  ув   ln ~
xi  ni   ln ~
xi  wi   yi  wi ,
n i 1
i 1
i 1
k
k
1 k
2
2
~
~
(3)
  Dв (Y )   (ln xi  ув )  ni  (ln xi  ув )  wi  ( yi  ув ) 2  wi ,
n i 1
i 1
i 1
x x
где ~
xi  i 1 i - середины интервалов. Можно использовать одну из приведенных для
2
2
оценивания параметров a и  2 формул. В зависимости от выбранной формулы для
удобства расчетов составляется таблица. Проведем расчеты, применяя для нахождения
k
оценок параметров формулы: а   yi  wi
i 1
k
и  2   ( yi  ув ) 2  wi ,
i 1
где yi  ln xi .
Таблица 2 – Расчетная таблица
№
( xi 1; xi ]
частота n i
~
хi
yi  ln ~
хi
wi
yi  wi
1
2
3
4
5
6
7
8
(0; 2]
(2; 4]
(4; 6]
(6; 8]
(8; 10]
(10; 12]
(12; 14]
(14; 16]
9
37
46
34
23
10
6
2
167
1
3
5
7
9
11
13
15
0
1,1
1,61
1,95
2,2
2,4
2,56
2,71
0,054
0,221
0,275
0,204
0,138
0,06
0,036
0,012
1
0
0,243
0,443
0,398
0,304
0,144
0,092
0,033
ув =1,657

( yi  yв ) 2  wi
0,148
0,069
0,001
0,018
0,041
0,033
0,029
0,013
0,352
Итак, а  ув  1,66 ;  2  0,35 ;   0,6 .
Функция плотности (1) может быть записана:
(ln x 1,66) 2
1
1 
0, 7
.
(4)
f ( x) 
 e
0,6  2 х
При решении практических задач представляет интерес задача планирования
объема будущих продаж. Можно оценить наиболее часто встречающуюся сумму,
истраченную на покупки, долю покупателей, которые потратят средства,
принадлежащие определенному ценовому интервалу. Так же среднее количество
истраченных денежных средств. Если распределение можно считать логарифмически
нормальным, с известными или оцененными параметрами, то для нахождения среднего
значения М ( Х ) случайной величины Х , при известных параметрах a и  2 , можно
воспользоваться формулой:
2
M ( X )  e a  0,5 .
(5)
По имеющимся данным можно сказать, что в среднем покупатели тратят на
покупки 6,26 тыс.руб., т.к. по формуле (5) имеем: M ( X )  e1,660,50,35  e1,835  6,26 .
Наиболее вероятное значение денежных средств, потраченных покупателями,
соответствует моде M o (X ) функции плотности f (x) , и может быть оценено по
формуле:
2
(6)
M o ( X )  ea  .
В
приведенном
примере,
используя
(6),
получим:
1,66  0,35
1,31
Mo (X )  e
 е  3,71, т.е. наиболее вероятно, что покупатель совершит
покупку на сумму 3,71 тыс. руб.
Доля покупателей, размер потраченных денежных средств которых
принадлежит определенному ценовому интервалу ( ;  ) , определяется по формуле:
(7)
P(  X   )  Фt2   Фt1  ,
ln   a
ln   a
где Фx  - функция Лапласа, и аргументы ее находятся: t1 
, а t2 
.


Например, можно определить вероятность того, что покупатель израсходует на
 ln 4  1,66 
покупки более 4 тыс. руб. По формуле (7) имеем: P(4  X  )  Ф   Ф
=
 0,6 
 1,39  1,66 
= Ф   Ф
 = Ф  Ф 0,27 =0,5+0,106=0,606. Итак, можно сказать, что
0,6


60,6 % покупателей от их общего числа тратят в магазине «NIKE» более 4 тыс. руб.
В заключение следует заметить, что сегодня деятельность в любой области
экономики, в частности для предпринимательской деятельности, требует от
специалиста применения современных методов работы, знания новейших достижений,
понимания научного языка. Знание основ математической статистики позволяет
определить наличие закономерностей на основе собранных данных, проанализировать
их для принятия обоснованных решений.
Список использованных источников
1.
Кремер, Н. Ш. Теория вероятностей и математическая статистика :
учебник / Н. Ш. Кремер. - / Москва : Юнити – Дана, 2012. – 551 с.
2.
Гмурман, В. Е. Руководство к решению задач по теории вероятностей и
математической статистике : учебное пособие для вузов / В.Е. Гмурман. - / Москва :
Высш.шк., 2004. – 404 с.
3.
Данко, П.Е. Высшая математика в упражнениях и задачах: учебное
пособие : в 2 ч. / П. Е. Данко, А.Г. Попов, Т.Я. Кожевников. - / Mосква: Высш. шк.,
2007. – 416с.