numerical analysis - Механико
advertisement

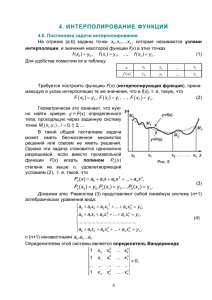
1. 1.1 Организационно-методический раздел. Название курса. Численный анализ. Направление - математика Раздел - общие математические и естественно-научные дисциплины Компонент 1.2 Цели и задачи курса. Дисциплина "Численный анализ " предназначена для студентов второго курса механико-математических факультетов университетов. Основной целью освоения дисциплины является изучение и практическое освоение студентами классических методов алгебраического интерполирования, интегрирования и итерационных методов решения нелинейных уравнений в одномерном случае. Для достижения поставленной цели выделяются задачи курса: 1) изучение теоретической части курса в соответствии с программой 2) решение цикла задач по курсу в соответствии с программой 3) реализация методов на ЭВМ и сдача вычислительного практикума 6) сдача экзамена в соответствии с учебным планом. 1.3 Требования к уровню освоения содержания курса. По окончании изучения указанной дисциплины студент должен - иметь представление о месте и роли изучаемой дисциплины среди других наук; - знать содержание программы курса, формулировки задач, условия применимости и характеристики методов интерполирования и интегрирования одномерных функций, решения нелинейных уравнений; - уметь определять точность интерполяционных и квадратурных формул, применимость метода последовательных приближений и метода Ньютона для приближения корня одномерной функции, реализовывать методы в виде программ для ЭВМ. 1.4 Формы контроля Итоговый контроль. Для контроля усвоения дисциплины учебным планом предусмотрен зачет и экзамен. Текущий контроль. В течение семестра выполняются домашние задания и контрольные работы. Выполнение указанных видов работ является обязательным для всех студентов. 2 Содержание дисциплины. 2.1 Новизна. Курс "Численный анализ " является традиционной дисциплиной математической подготовки студентов; его новизна состоит в том, что классический материал по этой дисциплине весьма обширен, а изложение его теоретических основ за 16 лекционных часов требует тщательного отбора тем и методов прежде всего удовлетворяющих критерию их использования на ЭВМ для решения широкого круга задач. Курс характеризуется математической строгостью изложения, большим числом предлагаемых теоретических и практических задач и упражнений. 2.2 Тематический план курса. Наименование разделов и тем Численный анализ Итого по курсу: Лекции 16 16 Количество ЛабораторСеминары ные работы 16 16 16 16 2.3 Содержание отдельных разделов и тем. Численный анализ 1. Алгебраические методы интерполирования. 1.1. Интерполяционный полином в форме Лагранжа. 1.2. Интерполяционный полином в форме Ньютона. 1.3. Оценка погрешности интерполирования 2. Интерполирование с кратными узлами. часов Самостоятельная работа 9 9 Всего часов 57 57 3. 4. 5. 6. 2.1. Представление интерполяционного полинома Эрмита в форме Лагранжа. 2.2. Представление интерполяционного полинома Эрмита в форме Ньютона. 2.3. Оценка погрешности интерполирования. Интерполирование кубическим сплайном 3.1. Определение и построение кубического сплайна. 3.2. Оценка погрешности. Численное дифференцирование. 4.1. Применение интерполяционного полинома для получения формул численного дифференцирования. 4.2. Оценка погрешности численного дифференцирования. 4.3. Некорректность численного дифференцирования. Численное интегрирование. 5.1. Интерполяционные квадратурные формулы. 5.2. Квадратуры Гаусса наивысшей алгебраической степени точности. 5.3. Сходимость квадратур Гаусса. 5.4. Устойчивость квадратурных формул. 5.5. Примеры квадратурных формул. 5.6. Составные квадратурные формулы. Итерационные методы решения нелинейных уравнений. 6.1. Принцип сжимающих отображений. 6.2. Метод простой итерации. 6.3. Метод Эйткена ускорения сходимости метода простой итерации. 6.4. Метод Ньютона. Случай простого корня. 6.5. Метод Ньютона с параметром. 2.4 Перечень примерных контрольных вопросов и заданий для самостоятельной работы. 1. Оценить объем арифметических операций вычисления значения интерполяционного полинома в форме Лагранжа. 2. Оценить объем арифметических операций вычисления коэффициентов (разделенных разностей) интерполяционного полинома в форме Ньютона. 3. Сравнить объемы вычислений при пересчете таблицы значений функции при добавлении нового интерполяционного узла с использованием интерполяционного полинома в форме Лагранжа и форме Ньютона. 4. Как связана проблема выбора оптимальных узлов интерполяции с полиномом, наименее уклоняющимся от нуля? 5. Как задать краевые условия для кубического сплайна по значением интерполируемой функции на сетке? Какие формулы численного дифференцирования можно применять и почему? 6. Оценить объем арифметических операций для построения кубического сплайна и вычисления его значения в произвольной точке. 7. Как определить, является ли квадратурная формула интерполяционной? 8. Как практически определить алгебраическую точность квадратурной формулы? 9. Построить квадратуру Гаусса на трех узлах и сравнить ее с формулой Симпсона. 10. Постройте алгоритм изменения сетки для вычисления интеграла с заданной точностью составной квадратурной формулой трапеций (и формулой Симпсона). n n 11. Для каких матриц отображение (x) x (Ax b) из R в R является сжимающим? 12. Постройте метод простой итерации для приближения положительного корня уравнения x n a 1 . 13. Постройте метод Ньютона для приближения положительного корня уравнения x n a 1 . 14. Сформулируйте и докажите сходимость метода Ньютона для гладких и выпуклых функций. 15. Постройте модификацию метода Ньютона с квадратичной скоростью сходимости для приближения p корня полинома (x 1) . 3 Учебно-методическое обеспечение дисциплины 3.1 Темы рефератов (курсовых работ). Не предусмотрено. 3.2 Образцы вопросов для подготовки к экзамену (дифференцированному зачету, зачету). Зачет по курсу заключается в сдаче работающей программы (реализующей тот или иной метод) с объяснением особенностей реализации и характеристик метода. Вопросы для подготовки к экзамену практически совпадают с программой курса "Численный анализ ". Ниже приводятся образец экзаменационного билета, содержащий теоретический вопрос и задачу по теме, отличающейся от первого вопроса: 1. Сходимость квадратур Гаусса для непрерывных функций. x 0.5 Исследуйте сходимость x 0 1, x n 1 x n n , n 0,1,... . 2 2. 3.3 1. 2. 3. 4. 5. 6. 2x n Список основной и дополнительной литературы. Бахвалов Н.С. Численные методы. - М.: Наука, 1975. Березин И.С., Жидков Н.П. Методы вычислений. Ч.1. - М.: Наука, 1966. Волков Е.А. Численные методы. - М.: Наука, 1987. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989. Мацокин А.М. Численный анализ (конспект лекций). mmfd.nsu.ru Для изучения дисциплин, которые предусматривают использование нормативно-правовых актов, указывать источник опубликования. Не предусмотрено. 3.4