Федеральное государственное автономное образовательное учреждение
высшего образования
«Крымский федеральный университет им. В. И. Вернадского»
Физико-технический институт
Кафедра компьютерной инженерии и моделирования
Практическая работа №4
«ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ»
по дисциплине
«Алгоритмы и методы вычислений»
Выполнил:
Студент 3 курса
Направления подготовки:
«Программная
инженерия»
Группа: ПИ-б-о-211
Оруджев Руслан
Камалович
Проверил:
Таран Е.П.
« »
2024г.
Оценка:
Подпись:
Симферополь, 2024
Цель работы:
1. Изучить и научиться отличать термины интерполяция, аппроксимация,
экстраполяция, сплайны, кривые Безье, полином Лагранжа, метод
наименьших квадратов.
2. Научиться использовать на практике наиболее эффективные алгоритмы
глобальной и локальной интерполяции.
3. Изучить устойчивые приемы численного дифференцирования.
4. Изучить метод численного интегрирования функций, заданных на
неравномерной сетке, с помощью сплайнов.
5. Написать программу, реализующую два
метода интерполяции
табличных значений:
1) Полином Лагранжа для глобальной интерполяции;
2) Кубический сплайн.
Пример
подготовить
самостоятельно,
обеспечив
возможность
изменения числовых данных на неравномерной сетке.
6. Указание: с помощью численных экспериментов выявить недостатки
интерполяции с помощью полинома Лагранжа. При построении
кубического сплайна коэффициенты находить численно путем решения
четырех диагональной СЛАУ методом прогонки.
Дополнительные задания (бонусы):
1) Построить сплайн Эрмита;
2) Построить кривые Безье;
3) Реализовать устойчивый алгоритм численного дифференцирования.
Ход работы:
1. Интерполяция и аппроксимация
Аппроксимация – это замена сложной функции (или табличных данных)
простой функцией, усредненно проходящей через данные точки. В общем
случае – это метод, состоящий в замене одних объектов другими, в том или
ином смысле близкими к исходным, но более простыми.
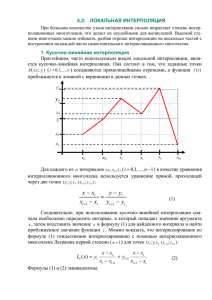
Интерполяция (вид аппроксимации) – это способ нахождения
промежуточных значений величины по имеющемуся дискретному набору
известных величин. При этом интерполянт точно проходит через имеющиеся
точки данных. Рассмотрим систему несовпадающих точек x(i) из некоторой
области. Пусть значения функции известны только в этих точках: Задача
интерполяции состоит в поиске такой функции из заданного класса функций,
которая точно проходит через узлы интерполяции.
Точки x(i) - называют узлами интерполяции, а их совокупность —
интерполяционной сеткой. Пары x(i), y(i) - называют точками данных или
базовыми точками, разность между «соседними» значениями - шагом
интерполяционной сетки. Он может быть, как переменным, так и постоянным.
Функцию F(x) —
называют интерполирующей функцией или
интерполянтом. Данные сами по себе не могут определить интерполянт. Для
фиксированного набора данных существует бесконечно много интерполянтов.
2. Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа - это многочлен минимальной
степени, принимающий данные значения в данном наборе точек. Для n + 1 пар
чисел:
где все x i различны, существует единственный многочлен L(x) степени не
более n, для которого L(x i) = yi. В простейшем случае (n = 1) — это линейный
многочлен, график которого — прямая, проходящая через две заданные точки.
Лагранж предложил способ вычисления таких многочленов:
где базисные полиномы определяются по формуле:
Полиномы Лагранжа используются для интерполяции, а также для
численного интегрирования. Пусть для функции f(x) известны значения y j =
f(xj) в некоторых точках. Тогда мы можем интерполировать эту функцию как:
В частности,
3. Интерполяция сплайнами
Описание метода:
Пусть отрезок [a,b] разбит на n равных частей [x i , x i+1], где xi=a+ih,
i=0,...,n, xn=b, h=(b-a)/n.
Сплайном называется функция, которая вместе с несколькими
производными непрерывна на всем заданном отрезке [a,b], а на каждом
частичном отрезке [xi , xi+1] в отдельности является некоторым алгебраическим
многочленом. Максимальная по
всем частичным отрезкам степень
многочленов называется степенью сплайна, а разность между степенью
сплайна и порядком наивысшей непрерывной на [a,b] производной - дефектом
сплайна.
Определение:
Функция Sn,(x) называется сплайном степени n дефекта ( -целое
число, 0 n+1) с узлами на сетке (: a=x0< <xi<...<xn=b), если:
а) на каждом отрезке [xi , xi+1] функция Sn,(x) является многочленом
степени n:
б)
(для целого k>0 через Ck =Ck [a,b] обозначается множество k раз
непрерывно дифференцируемых на [a,b] функций).
4. Кривые Безье
Кривая Безье — это параметрическая кривая, задаваемая выражением:
где Pi — функция компонент векторов опорных вершин, а bi,n(t) —
базисные функции кривой Безье, называемые также полиномами Бернштейна.
где n — степень полинома, i — порядковый номер опорной вершины.
В параметрической форме кубическая кривая Безье (n = 3) описывается
следующим уравнением:
Четыре опорные точки P 0, P1, P2 и P3, заданные в 2-х или 3-мерном
пространстве определяют форму кривой. Линия берёт начало из точки P0
направляясь к P 1 и заканчивается в точке P 3 подходя к ней со стороны P 2. То
есть кривая не проходит через точки P 1 и P2, они используются для указания
её направления. Длина отрезка между P 0 и P1 определяет, как скоро кривая
повернёт к P 3.
В матричной форме кубическая кривая Безье записывается следующим
образом:
где MB называется базисной матрицей Безье:
В качестве функции мы взяли параболу: y=cos(x)
Вывод программы, реализующей два метода интерполяции
табличных значений: Полином Лагранжа для глобальной интерполяции
и Кубический сплайн:
Вывод программы, отображающий кривую Безье:
Вывод программы, отображающий сплайн Эрмита:
Вывод: В данной практической работе были рассмотрены основные
понятия интерполяции, аппроксимации. Были изучены такие методы
интерполяции, как полином Лагранжа и кубический сплайн. Была написана
программа, реализующая эти два метода интерполяции табличных значений.
Для демонстрации был выбран пример интерполяции параболической
функции y = x^2 на неравномерной сетке. Результаты показали, что полином
Лагранжа хорошо аппроксимирует функцию в целом. В то же время
кубический сплайн, может отклоняться от исходной функции. Также были
изучены методы построения сплайна Эрмита и кривых Безье. Сплайн Эрмита
использует не только значения функции в узлах, но и значения производных,
что позволяет получить более гладкую кривую. Кривые Безье задаются
опорными точками и обладают рядом полезных свойств, таких как
принадлежность выпуклой оболочке опорных точек, что делает их удобными
для использования в компьютерной графике и САПР. Таким образом, в ходе
работы были изучены и реализованы на практике различные методы
интерполяции, аппроксимации, что позволило лучше понять их достоинства,
недостатки и области применения.
ПРИЛОЖЕНИЕ
1. Программа, которая реализует два метода интерполяции табличных
значений: Полином Лагранжа для глобальной интерполяции и
Кубический сплайн:
import numpy as np
import matplotlib.pyplot as plt
def lagrange_interpolation(x, y, x_new):
"""
Интерполяция с помощью полинома Лагранжа
x: массив значений x
y: массив значений y
x_new: массив новых значений x, для которых нужно вычислить y
"""
n = len(x) # Количество исходных точек
y_new = np.zeros_like(x_new) # Инициализация массива для
интерполированных значений y
# Вычисление интерполированных значений y для каждого x_val в
x_new
for i, x_val in enumerate(x_new):
sum = 0
for j in range(n):
product = y[j]
for k in range(n):
if k != j:
product *= (x_val - x[k]) / (x[j] - x[k])
sum += product
y_new[i] = sum
return y_new
def cubic_spline_interpolation(x, y, x_new):
"""
Интерполяция с помощью кубического сплайна
x: массив значений x
y: массив значений y
x_new: массив новых значений x, для которых нужно вычислить y
"""
n = len(x) # Количество исходных точек
h = np.diff(x) # Вычисление разностей между соседними значениями x
a = np.zeros(n) # Инициализация массива для коэффициентов a
b = np.zeros(n) # Инициализация массива для коэффициентов b
c = np.zeros(n) # Инициализация массива для коэффициентов c
d = np.zeros(n) # Инициализация массива для коэффициентов d
# Построение системы уравнений для коэффициентов
a[0] = y[0] # Присваивание начального значения y
c[n-1] = 0 # Краевое условие для последней точки
for i in range(1, n):
a[i] = y[i] # Присваивание остальных значений y
A = np.zeros((n, n)) # Инициализация матрицы системы уравнений
B = np.zeros(n) # Инициализация вектора правой части системы
уравнений
for i in range(1, n-1):
A[i, i-1] = h[i-1]
A[i, i] = 2 * (h[i-1] + h[i])
A[i, i+1] = h[i]
B[i] = 6 * ((y[i+1] - y[i]) / h[i] - (y[i] - y[i-1]) / h[i-1])
c[1:-1] = np.linalg.solve(A[1:-1, 1:-1], B[1:-1])
for i in range(n-1):
d[i] = (c[i+1] - c[i]) / (3 * h[i])
b[i] = (a[i+1] - a[i]) / h[i] - h[i] * (c[i+1] + 2 * c[i]) / 3
# Вычисление значений y для новых x
y_new = np.zeros_like(x_new)
for i, x_val in enumerate(x_new):
j = np.searchsorted(x, x_val) - 1
dx = x_val - x[j]
y_new[i] = a[j] + b[j] * dx + c[j] * dx**2 / 2 + d[j] * dx**3 / 6
return y_new
# Пример использования
x = np.array([-4, -3.5, -2.9, -2.2, -1.6, -1.2, -1, -0.7, -0.5, -0.3, 0, 0.4, 0.8, 1.8, 2,
2.8, 3.5, 3.8, 3.9, 4])
y = np.cos(x)
# Функция синуса
x_new = np.linspace(-4, 4, 200)
y_true = np.cos(x_new)
# Вычисление значений y с помощью полинома Лагранжа
lagrange_y = lagrange_interpolation(x, y, x_new)
# Вычисление значений y с помощью кубического сплайна
cubic_spline_y = cubic_spline_interpolation(x, y, x_new)
# Визуализация результатов
plt.figure(figsize=(10, 6))
plt.plot(x_new, lagrange_y, label='Полином Лагранжа')
plt.plot(x_new, cubic_spline_y, label='Кубический сплайн')
plt.plot(x_new, y_true, '--', label='Истинная функция')
plt.scatter(x, y, c='r', label='Данные')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Интерполяция параболы y = x^2')
plt.legend()
plt.xlim(-2.5, 2.5) # Установка пределов по оси x
plt.ylim(-1, 5) # Установка пределов по оси y
plt.show()
2. Программа, которая строит кривую Безье:
import numpy as np
import matplotlib.pyplot as plt
def bezier_curve(points, num_points=100):
"""
Построение кубической кривой Безье по заданным опорным точкам.
Параметры:
points (list): список координат опорных точек [(x0, y0), (x1, y1), (x2, y2),
(x3, y3)]
num_points (int): количество точек для построения кривой
Возвращает:
x (np.ndarray): массив координат x кривой Безье
y (np.ndarray): массив координат y кривой Безье
"""
n = len(points) - 1
# Создание массива параметров t
t = np.linspace(0, 1, num_points)
# Расчет координат кривой Безье
x = np.zeros(num_points)
y = np.zeros(num_points)
for i in range(num_points):
for j in range(n + 1):
bernstein = np.math.comb(n, j) * (1 - t[i])**(n - j) * t[i]**j
x[i] += points[j][0] * bernstein
y[i] += points[j][1] * bernstein
return x, y
# Пример использования
points = [(1, 1), (2, 5), (5, 2), (6, 6)]
x, y = bezier_curve(points)
# Построение графика
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='Кривая Безье')
plt.scatter([p[0] for p in points], [p[1] for p in points], c='r', label='Опорные
точки')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Кривая Безье')
plt.legend()
plt.grid(True)
plt.show()
3. Программа, которая строит сплайн Эрмита:
import numpy as np
import matplotlib.pyplot as plt
def hermite_spline_interpolation(x, y, dydx, x_new):
"""
Интерполяция с помощью сплайна Эрмита
x: массив значений x
y: массив значений y
dydx: массив значений производных dy/dx в узлах интерполяции
x_new: массив новых значений x, для которых нужно вычислить y
"""
n = len(x) # Количество исходных точек
m = len(x_new) # Количество новых точек
y_new = np.zeros(m) # Инициализация массива для интерполированных
значений y
# Вычисление коэффициентов сплайна Эрмита для каждого интервала
for i in range(n - 1):
h = x[i + 1] - x[i]
t = (x_new - x[i]) / h
# Базисные функции сплайна Эрмита
h00 = 2 * t ** 3 - 3 * t ** 2 + 1
h10 = t ** 3 - 2 * t ** 2 + t
h01 = -2 * t ** 3 + 3 * t ** 2
h11 = t ** 3 - t ** 2
# Вычисление значений y для точек x_new, попадающих в интервал [x[i],
x[i+1]]
idx = np.logical_and(x_new >= x[i], x_new < x[i + 1])
y_new[idx] = y[i] * h00[idx] + h * dydx[i] * h10[idx]
if i < n - 1:
y_new[idx] += y[i + 1] * h01[idx] + h * dydx[i + 1] * h11[idx]
return y_new
# Пример использования
x = np.linspace(-2 * np.pi, 2 * np.pi, 11)
y = np.sin(x) # Функция y = sin(x)
dydx = np.cos(x) # Производная dy/dx = cos(x)
x_new = np.linspace(-2 * np.pi, 2 * np.pi, 100)
y_true = np.sin(x_new)
# Вычисление значений y с помощью сплайна Эрмита
hermite_y = hermite_spline_interpolation(x, y, dydx, x_new)
# Визуализация результатов
plt.figure(figsize=(10, 6))
plt.plot(x_new, hermite_y, label='Сплайн Эрмита')
plt.plot(x_new, y_true, '--', label='Истинная функция')
plt.scatter(x, y, c='r', label='Данные')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Интерполяция функции y = sin(x)')
plt.legend()
plt.xlim(-2 * np.pi - 0.5, 2 * np.pi + 0.5)
plt.ylim(-1.2, 1.2)
plt.show()