Работа №1. ИССЛЕДОВАНИЕ НЕСТАЦИОНАРНОГО РЕЖИМА В
МАРКОВСКОЙ СИСТЕМЕ МАССОВОГО ОБСЛУЖИВАНИЯ
Цель работы - изучение методов исследования нестационарного
режима в Марковской СМО с ограниченной длиной очереди (типа М/М/I) и
оценка влияния параметров СМО на длительность переходного процесса.
Порядок выполнения работы.
1. Ознакомиться с методическими указаниями.
2. Для заданного варианта СМО с помощью стандартной программы
определить вероятности Pk(t). Построить графики Pk(t).
3. Определить длительность переходного процесса в СМО, как время
входа всех Pk(t) в 5%-ю трубку.
4. Рассчитать основные характеристики СМО (среднее число занятых
каналов, среднюю длину очереди, вероятность, что поступившее требование
будет обслужено) в переходном и установившемся режимах.
5. Рассчитать основные характеристики СМО в стационарном режиме,
используя формулы финальных вероятностей. Сравнить результаты с
аналогичными значениями, полученные в п. 4. Оценить их точность.
Используя формулу Литтла вычислить среднее время нахождения
требования в очереди, общее время нахождения требования в
системе.
6. Для заданного варианта СМО исследовать зависимость основных
характеристик СМО от варьируемых параметров. Построить графики.
7. Оформить отчет, в котором привести описание исследуемой СМО,
уравнения размножения и гибели для заданного базового варианта СМО,
основные соотношения, результаты расчётов, графики, выводы на основе
полученных результатов.
8. Ответить на контрольные вопросы.
ВАРИАНТЫ ЗАДАНИЙ
N
1.
2.
3.
4.
5.
6.
7.
8.
n
2
3
1, 2, 3, 4, 10, 20
1, 2, 3, 4, 10, 20
1, 2, 3, 4, 10, 20
2
3
1, 2, 3, 4, 10, 20
m
1, 2, 3, 4, 10, 20
1, 2, 3, 4, 10, 20
2
3
2
1, 2, 3, 4, 10, 20
1, 2, 3, 4, 10, 20
2
5
7
8
10
5
6
10
9
2
2
2
2
1
2
3
3
β
0,9
0,95
0,9
0,95
0,9
0,95
0,9
0,95
Основные положения.
Имеется n - канальная СМО. На вход системы поступает простейший
поток требований, с интенсивностью λ. Время обслуживания требований в
каждом канале обслуживания распределено по экспоненциальному закону, с
параметром μ (интенсивность обслуживания). Максимальная длина очереди
ограничена числом m. Если хотя один канал свободен, то пришедшее
требование сразу поступает на обслуживание. Если все каналы заняты,
пришедшее требование становится в очередь. Если в очереди уже находятся
m требований, то пришедшее требование получает отказ в обслуживании и
покидает систему необслуженным.
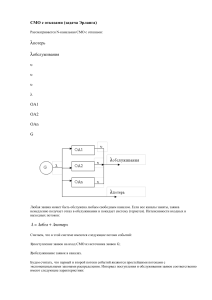
Схематически СМО можно представить в виде
Здесь входной поток требований - простейший Пуассоновский поток,
который обладает свойствами стационарности, ординарности и отсутствия
последействия. В нём число требований, поступающих в единицу времени
распределено по закону Пуассона с интенсивностью λ.
Время обслуживания в выходном потоке (интервал между двумя
соседними обслуженными требованиями в канале обслуживания) подчинено
экспоненциальному закону распределения с интенсивностью µ.
Обозначим K(t) - число требований, находящихся в СМО в момент
времени t. Для описания процесса функционирования K(t) необходимо знать
вероятности Pk (t) = P{K(t)=k}, где 0≤k≤(n+m).
Если все потоки событий, переводящие СМО из состояния в состояние
простейшие, то процесс, протекающий в такой системе, будет Марковским.
Случайный процесс называется Марковским – если для любого момента
времени 𝑡0 , вероятностные характеристики процесса в будущем (t > 𝑡0 )
зависят только от его состояния в данный момент времени𝑡0 (в настоящем) и
не зависят от того, когда и как система пришла в это состояние (в прошлом).
В нашем случае процесс K(t) можно рассматривать как Марковский
процесс
размножения
и
гибели.
Вероятности
состояний
системы
описываются уравнениями Колмогорова-Чепмена [1]:
𝑑𝑃𝑜 (𝑡)
= −λ ∗ 𝑃𝑜 (𝑡) + 𝜇 ∗ 𝑃1 (𝑡)
𝑑𝑡
𝑑𝑃𝑘 (𝑡)
= −(λ + 𝑘𝜇) ∗ 𝑃𝑘 (𝑡) + λ ∗ 𝑃𝑘−1 (𝑡) + (𝑘 + 1)𝜇 ∗ 𝑃𝑘+1 (𝑡) 1 ≤ 𝑘 < 𝑛
𝑑𝑡
𝑑𝑃𝑘 (𝑡)
= −(λ + 𝑛𝜇) ∗ 𝑃𝑘 (𝑡) + λ𝑃𝑘−1 (𝑡) + 𝑛𝜇 ∗ 𝑃𝑘+1 (𝑡)
𝑛 ≤𝑘 <𝑛+𝑚
𝑑𝑡
𝑑𝑃𝑛+𝑚 (𝑡)
= −𝑛𝜇 ∗ 𝑃𝑛+𝑚 (𝑡) + λ ∗ 𝑃𝑛+𝑚−1 (𝑡)
𝑑𝑡
В случае высокого порядка системы дифференциальных уравнений
анализ нестационарного режима работы СМО аналитическим методом
затруднен. В этих случаях для их исследования используют численные
методы интегрирования системы на ЭВМ (Рунге - Кутты, Эйлера и других).
Так как исследуемая СМО имеет конечное число состояний, то, при
достаточно длительном функционировании, процесс входит в режим
статистического равновесия. Этот режим характеризуется стационарным
распределением вероятностей, не зависящим от начальных условий:
lim Pk (t) Pk для всех k=0,1,…,(n+m) .
t
Имея графики изменения всех Pk(t) можно найти время переходного
процесса (время достижения значений финальных вероятностей с заданной
точностью – время вхождения в δ% «трубку»).
Рассмотрим поведение СМО как в переходном, так и в стационарном
режиме. Для получения значений всех Pk (t) необходимо задать начальные
условия.
В качестве начальных условий примем (на начало работы в системе нет
требований):
P0( 0 ) 1, Pk ( 0 ) 0, k 1,2,...,n m.
Зная значения вероятностей Pk(t) вычислить основные характеристики
рассматриваемой СМО как функции времени (среднее число занятых
каналов, средняя длина очереди, вероятность, что поступившее
требование будет обслужено) и построить соответствующие графики.
При оценке этих результатов следует иметь в виду, что время
измеряется в условных единицах, то есть в тех же единицах, которые были
использованы при задании интенсивностей и .
Имея графики изменения всех Pk(t) можно найти время переходного
процесса (время достижения значений всех финальных вероятностей с
заданной точностью – время вхождения в δ% «трубку»).
Для нахождения значений Pk, 0≤k≤(n+m) и основных характеристик
СМО
в
стационарном
режиме
использовать
формулы
финальных
вероятностей.
𝐏𝐤 =
𝛒𝐤
𝐤!
∗ 𝐏𝟎 ,
1≤k≤n
𝛒
𝛒𝐧
𝐧
𝐧!
𝐏𝐤 =( )𝐤−𝐧 ∗ 𝐏𝐧 =
𝐏𝟎 = [𝟏 + ∑𝐧−𝟏
𝐤=𝟏
𝛒𝐤
+
𝐤!
𝛒
*( )𝐤−𝐧 ∗ 𝐏𝟎 , n≤k≤n+m,
𝐧
𝛒 𝐤−𝐧 −𝟏
𝛒𝐧
∑𝐧+𝐦 ( )
𝐧! 𝐤=𝐧 𝐧
]
Или иначе
𝐏𝟎 = [𝟏 + ∑𝐧−𝟏
𝐤=𝟏
𝛒𝐤
+
𝐤!
𝛒𝐧
𝐧!
∗
𝛒
𝟏−( ⁄𝐧)𝐦+𝟏 −𝟏
]
𝛒
𝟏− ⁄𝐧
Основные характеристики СМО в стационарном режиме будут:
1) Вероятность того, что пришедшее требование получит отказ.
𝐏отк = 𝐏𝐧+𝐦
2) Вероятность того, что пришедшее требование будет обслужено.
𝐏обс = 𝟏 − 𝐏отк = 𝟏 − 𝐏𝐧+𝐦
3) Среднее число занятых каналов.
mкан = 𝐚𝐧 = ∑𝐧𝐤=𝟏 𝐤 ∗ 𝐏𝐤 + n ∗ ∑𝐧+𝐦
𝐤=𝐧+𝟏 𝐏𝐤
Или, иначе:
mкан = 𝛒 ∗ 𝐏обс
4) Средняя длина очереди.
𝐦𝐋 = ∑𝐧+𝐦
𝐤=𝐧+𝟏(𝑘 − 𝑛) ∗ 𝐏𝐤 =
Используя формулу Литтла вычислить:
8) Среднее время нахождения требования в очереди
𝐭 оч =
𝟏
𝛌сист
*𝐦𝐋 =
𝟏
𝛌∗𝐏обс
*𝐦𝐋
9) Общее время нахождения требования в системе
𝐭 сист = 𝐭 оч + 𝐭 кан =
𝟏
𝛌сист
(𝐦𝐋 + 𝐚𝐧 ) =
𝟏
𝛌∗𝐏обс
∗ [𝐦𝐋 + 𝛒 ∗ 𝐏обс ] .
Контрольные вопросы.
1. Какие
случайные
процессы
называются
Марковскими?
Какова
специфика математического описания этих процессов?
2. Почему процесс обслуживания в СМО типа M/M/n
является
Марковским?
3. Поясните, применительно
существования
к рассматриваемой системе, условия
стационарного
режима
(режима
статистического
равновесия).
4. В чем состоят затруднения при исследовании нестационарного
режима?
5. Перечислите известные Вам численные методы решения систем
дифференциальных уравнений. В чем состоит метод Рунге - Кутты?
Опишите вычислительную процедуру метода.
6. Как
влияют
на
основные
характеристики
СМО
исследуемые
параметры?
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Бомас В.В.,Булыгин В.С. Элементы теории Марковских процессов и ее
технические приложения: Учебное пособие. - М.: МАИ, 1980.
1. Вентцель.
Е.С.
Исследование
операций:
задачи,
принципы,
методология. – М.: Наука 1988 – 208с.
2. Дегтярев Ю.И. Исследование операций. Учебник. М.: Высшая школа,
1986 г, 320 с.:ил.
3. Бомас В.В., Красовская М.А., Ескин В.И. Лабораторные работы по
курсу «Исследование операций». М.: МАИ, 1992. – 28 с.:ил.
4. Дунин – Барковский И.В., Смирнов Н.В. теория вероятностей и
математическая статистика. – М.: Гостехтеориздат, 1955.