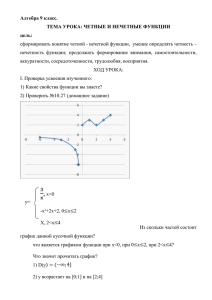
Перечислите свойства функции у = f(х), график которой
advertisement

Четные и нечетные функции В предыдущем параграфе мы обсуждали только те свойства функций, которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе. Определение 1. Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х). Определение 2. Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х). Пример 1. Доказать, что у = х4 — четная функция. Решение. Имеем: f(х) = х4, f(-х) = (-х)4. Но (-х)4 = х4. Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной. Аналогично можно доказать, что функции у — х2,у = х6,у — х8 являются четными. Пример 2. Доказать, что у = х3~ нечетная функция. Решение. Имеем: f(х) = х3, f(-х) = (-х)3. Но (-х)3 = -х3. Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной. Аналогично можно доказать, что функции у = х, у = х5, у = х7 являются нечетными. Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х3, у = х5, у = х7 — нечетные функции, тогда как у = х2, у = х4, у = х6 — четные функции. И вообще для любой функции вида у = х" (ниже мы специально займемся изучением этих функций), где n — натуральное число, можно сделать вывод: если n — нечетное число, то функция у = х" — нечетная; если же n — четное число, то функция у = хn — четная. Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х). Итак, функция может быть четной, нечетной, а также ни той ни другой. Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность. В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как [0, +оо), (-2, 3), [-5, 5) — несимметричные множества. Если функция у = f (х) — четная или нечетная, то ее область определения D (f) — симметричное множество. Если же D (f) — несимметричное множество, то функция у = f(х) не является ни четной, ни нечетной. Учитывая сказанное, рекомендуем при исследовании функции на четность использовать следующий алгоритм. Алгоритм исследования функции у = f(х) на четность 1. Установить, симметрична ли область определения функции. Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то переходить ко второму шагу алгоритма. 2. Найти f(-х). 3. Сравнить f (x)= f (-x) а) если f(-х) = f(х), то функция — четная, б) если f(-х) = -f(х), то функция — нечетная; в) если хотя бы в одной точке х є Х выполняется соотношение f(-х) = f(х) и хотя бы в одной точке х є X выполняется соотношение f(-х) = -f(х), то функция не является ни четной, ни нечетной. Пример 3. Исследовать на четность функцию: Решение: <span style="font-weight: bold;" />а) у = f(x), где 1) Функция определена при всех значениях х, кроме х = 0. Следовательно,D (f) — симметричное множество. 2) 3) Замечаем, что для любого ж из области определения функции выполняется равенство f(x) = f(x). Таким образом, четная функция. б) 1) Функция определена при всех значениях х, кроме х = 0. Следовательно, D(f) — симметричное множество. 2) 3) Замечаем, что для любого х из области определения функции выполняется равенство f(-х) = -f(х). Таким образом, в) 1) Функция определена во всех точках х, кроме тех, которые обращают знаменатель дроби в нуль. Из условия х2 - 9 = 0 находим х = ± 3. Значит, область определения функции — числовая прямая, из которой удалены две точки: 3 и -3. Это — симметричное множество. 2) 3) Сравнив f(-х) и f(х), замечаем, что, скорее всего, не выполняются ни тождество f(-х) = f(х), ни тождество f(-х) = -f(х). Чтобы в этом убедиться, возьмем конкретное значение х, например х = 4. Имеем: f(4) = О, а Таким образом, функция не является ни четной, ни нечетной. г) Функция определена при условии т.е. на луче [3, +оо). Этот луч — несимметричное множество, значит, функция не является ни четной, ни нечетной. Пример 4. Исследовать на четность функцию: Решение. а) D(f) = [-2,2) — симметричное множество, и для всех х выполняется равенство | -х | = | х |. Значит, заданная функция — четная. б) D(f) = [-3, 3) — несимметричное множество. В самом деле, точка -3 принадлежит полуинтервалу [-3, 3), а противоположная точка 3 не принадлежит этому полуинтервалу. Значит, функция не является ни четной, ни нечетной. в) D (f) = (-5, 5) — симметричное множество и (-x)3 = -ж3 для всех х из интервала (-5, 5). Значит, заданная функция — нечетная. г) Функция задана на полуинтервале, который не является симметричным множеством. Значит, функция — ни четная, ни нечетная. Теперь обсудим геометрический смысл свойства четности и свойства нечетности функции. Пусть у = f(x) — четная функция, т.е. f(x) = f(х) для любого х е . Рассмотрим две точки графика функции: D(х; f(х)) и В(-х; f(-х)). Так как f(-х) = f(х), то у точек А и В абсциссы являются противоположными числами, а ординаты одинаковы. Эти точки симметричны относительно оси у (рис. 73). Таким образом, для каждой точки А графика четной функции у = f(х) существует симметричная ей относительно оси у точка В того же графика. Это означает, что график четной функции симметричен относительно оси у. Пусть у = f(х) — нечетная функция, т.е. f(-х) = D(х) для любого х е D(f). Рассмотрим две точки графика функции: А(х; f(х)) и В(-х; f(-х)). Так как f(-х) = f(х), то у точек А и В абсциссы являются противоположными числами и ординаты являются противоположными числами. Эти точки симметричны относительно начала координат (рис. 74). Таким образом, для каждой точки А графика нечетной функции у = f(х) существует симметричная ей относительно начала координат точка В того же графика. Это означает, что график нечетной функции симметричен относительно начала координат. Верны и обратные утверждения: 1) Если график функции у = f(х) симметричен относительно оси ординат, то у = f(х) — четная функция. В самом деле, симметрия графика функции у = f(х) относительно оси у означает, что для всех х из области определения функции справедливо равенство f(-х) = f(х), т.е. у = f(х) — четная функция. 2) Если график функции у = f(х) симметричен относительно начала координат, то у = f(х) — нечетная функция. Симметрия графика функции у = f(х) относительно начала координат означает, что для всех х из области определения функции справедливо равенство f(-х) = f(х), т.е. у — f(х) — нечетная функция. Пример 5. Исследовать на четность функцию Решение. Первый способ. Имеем Значит, для любого х из D(f) справедливо равенство f(-х) = f(х), т.е. функция является четной. Второй способ. Графиком функции служит полуокружность с центром в начале координат и радиусом 3 (см. рис.52 из § 9), она симметрична относительно оси у. Это означает, что — четная функция. А.Г. Мордкович Алгебра 9 класс Урок алгебры по теме "Свойства функций". 9-й класс Калинкина Елена Николаевна, учитель математики Разделы: Преподавание математики Тип урока: урок-практикум. Цель урока: расширить представление о свойствах функции. Задачи урока: 1. Развивать умение описывать свойства функции по заданному графику. 2. Формировать познавательную активность учащихся. 3. Воспитывать аккуратность при построении графиков функций. Оборудование: проектор, компьютер, мультимедийный продукт, распечатанные листы с графиками функций, бланки для ответов на тест, учебник “Алгебра, 9 класс” Ю.Н.Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов (М.: Просвещение, 2012 год). Структура урока: 1. Ознакомление с темой урока, постановка его целей (2 мин). 2. Актуализация знаний учащихся: а) повторение теоретического материала (4 мин); б) повторение графиков функций. (5 мин). 3. Отработка свойств функции (10 мин). 4. Психофизиологическая пауза (2 мин). 5. Закрепление материала. Самостоятельная работа (13 мин). 6. Объяснение домашнего задания (2 мин). 7. Подведение итогов урока (2 мин). Ход урока 1. Ознакомление с темой урока, постановка его целей. 2. Актуализация знаний учащихся. Повторение теоретического материала: Дать определение функции. Что такое область определения функции? Что такое область значений функции? Дать определение нулей функции. Дать определение промежутков знакопостоянства функции. Дать определение возрастающей функции. Дать определение убывающей функции. Даны графики функций. Найти соответствие между графиками функций и их названиями. Презентация. Слайды 2-6 а) д) б) в) е) >0 ж) <0 г) х2 < 0 з) Учащимся раздаются бланки для заполнения. На работу отводится 1 мин. . Проверяем ответы. Вызываю к доске одного из учащихся для заполнения таблицы. Остальным учащимся предлагаю поменяться бланками с соседом и выполнить взаимопроверку. 3. а) Устная работа. На рисунке изображен график функции переменной , при которой: . Найдите значения а) > 0, < 0, = 0; б) функция возрастает, убывает; в) функция на отрезке принимает наибольшее значение, наименьшее значение. Презентация. Слайд 7 б) разбираем задание из учебника: № 36. D(g) = [ – 5; 5]. E(g) = [– 4; 6]. g (x) = 0 x = – 3. g (x) > 0 x (– 3; 5]; g (x) < 0 x [– 5;– 3). 5. g(x) возрастает при x [– 5; 0] u [2; 5]; g (x) убывает при x [0; 2]. 1. 2. 3. 4. в) выполняем задание из учебника: № 38: Начертите график какой-либо функции с областью определения [– 3; 4] так, чтобы эта функция: а) возрастала в промежутке [– 3; 0] и убывала в промежутке [0; 4]; б) убывала в промежутке [– 3; 1] и возрастала в промежутке [1; 4]. К доски выходят два ученика и выполняют эту работу. 4. Психофизиологическая пауза. Ученики выполняют зарядку для глаз. 5. Закрепление материала. Самостоятельная работа. Провести исследование функции по готовым чертежам. Презентация. Слайд 8 1 вариант Перечислите свойства функции у = f(х), график которой изображен на рисунке: 1) Область определения функции: D(f) = ________________ 2) Область значений функции: E (f) = ________________ 3) Нули функции:_____________________________________ 4) Промежутки знакопостоянства функции: f(x) > 0 при _________________________________ f(х) < 0 при ________________________________ 5) Функция убывает на промежутке _________________________ Функция убывает на промежутке ____________________________ Презентация. Слайд 9 2 вариант Перечислите свойства функции у = f(х), график которой изображен на рисунке: 1) Область определения функции: D(f) = _______________________________ 2) Область значений функции: E (f) = __________________________________ 3) Нули функции:____________________________________________________ 4) Промежутки знакопостоянства функции: f(x) > 0 при ________________________________________________ f(х) < 0 при ________________________________________________ 5) Функция убывает на промежутке ____________________________________ Функция убывает на промежутке _____________________________________ Ответы к самостоятельной работе: 1 вариант 2 вариант 1) D(f) = [– 6; 7] 2) E (f) = [– 3; 5] 1) D(f) = [– 4; 8] 2) E (f) = [-2; 4] 3) f(x) = 0, х = – 6; х = – 2 3) f(x) = 0, х = – 2; х = 3; х = 8 4) f(x) > 0 при х 4) f(x) > 0при х f(х) < 0 при х [– 6; – 2) 5) f(x) возр при х f(x) убыв при х (– 2; 7] [– 4; 2] f(х) < 0 при х [– 4;– 2) и (3; 8] (– 2; 3) 5) f(x) возр при х [– 6; – 4] и [2; 7] f(x) убыв при х [0; 6] [– 4; 0] и [6; 8] Презентация. Слайд 10 Учащиеся самостоятельно выполняют работу в тетрадях, после этого проводят взаимопроверку по готовым ответам и оценивают работу соседа. 6. Объяснение домашнего задания (2 мин). По учебнику: повторить § 2, № 35( записать свойства функции), № 39(а,б) (построить графики), № 52 (в,г) ( повторение – квадратные уравнения). 7. Подведение итогов урока (2 мин). Вопросы на повторение: Дать определение функции. Что такое область определения функции? Что такое область значений функции? Дать определение нулей функции. Дать определение возрастающей (убывающей) функции. Сообщаются оценки за урок.