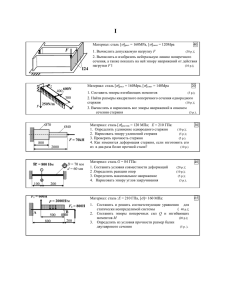
Практикум по сопротивлению материалов.

Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Институт новых информационных технологий
Государственного образовательного учреждения
высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Г.С. Лейзерович, В.С. Симонов
ПРАКТИКУМ
ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Утверждено в качестве учебного пособия
Ученым советом Государственного образовательного учреждения
высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Комсомольск-на-Амуре 2005
УДК 539.3 (075)
ББК 30.121 я7
Л 42
Лейзерович Г.С., Симонов В.С.
Л 42 Практикум по сопротивление материалов: Учебное пособие. – Комсомольск-наАмуре: Государственное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре гос. техн. ун-т». – 56 с.
ББК 30.121 я7
©
Государственное образовательное учреждение высшего профессионального
образования «Комсомольский-на-Амуре
государственный технический университет», 2005.
©
Институт новых информационных технологий Государственного образовательного учреждения высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет», 2005.
Предисловие
ПРЕДИСЛОВИЕ
Знать – вовсе не значит понимать. Это –
только держать в памяти то, что ей дали на
хранение
Мишель Эйкем де Монтень
Настоящее учебное пособие включает в себя программу традиционного курса сопротивления материалов, вопросы для самоконтроля, задания и варианты практических задач по основным разделам курса, примеры решения этих задач, а также перечень рекомендуемой литературы.
Рабочая программа в полном объеме определяет необходимый уровень дисциплины «Сопротивление материалов», читаемой кафедрой теоретической и прикладной
механики студентам машиностроительных специальностей Государственного образовательного учреждения высшего профессионального образования «Комсомольский-наАмуре государственный технический университет».
Вопросы для самоконтроля, по мнению авторов, помогут читателю лучше усвоить
пройденный теоретический материал и подготовиться к экзамену по курсу.
Решение практических задач преследует следующие основные цели:
 развить у вас самостоятельное технического мышление, умение и навыки
применения теоретических знаний при решении практических вопросов;
технику вычислений, способность работы со справочной и технической
литературой;
 закрепить и углубить знания по изучаемой дисциплине, приобрести навыки оформления технических расчетов.
При решении задач авторы рекомендуют вам придерживаться следующих советов.
Прежде чем воспользоваться той или иной формулой для определения напряженного и деформированного состояния конструкции, необходимо убедиться в том, что вы
действительно понимаете физический смысл всех величин, входящих в используемую
формулу. Необходимо также убедиться, что эта формула применима к вашему конкретному случаю.
Подставляя в формулы соответствующие нагрузки и размеры конструкции, следует предварительно убедиться, что они выражены в одной системе единиц и, в связи с
этим, не напутаны порядки чисел.
Самое серьезное внимание должно быть обращено на математические вычисления. Не следует гнаться за чрезмерной точностью. Надо придерживаться основных правил приближенных вычислений. За редким исключением, точность расчетов не должна
превышать трех значащих цифр, поскольку окончательный ответ, полученный в результате решения задачи, не может быть точнее тех приближенных предпосылок, которые были заложены в расчетные формулы.
Настоящее пособие может быть полезно и для студентов других специальностей,
изучающих сопротивление материалов, но в меньшем объеме.
Авторы заранее благодарят всех читателей, которые пожелают указать на неизбежные недостатки настоящего пособия.
1. Рабочая программа
4
1.
РАБОЧАЯ ПРОГРАММА
ТЕМЫ КУРСА
Введение. Основные положения и понятия
Задачи курса сопротивления материалов по изучению напряженнодеформированного состояния наиболее простых элементов конструкций. Краткий исторический очерк. Связь курса с общенаучными, общеинженерными и специальными
дисциплинами. Внешние силы и их классификация. Основные объекты, изучаемые в
курсе сопротивления материалов: стержень, пластина, оболочка. Основные свойства
деформируемого твердого тела: упругость, пластичность, изотропность и анизотропность. Деформации и перемещения. Основные допущения. Метод сечений. Внутренние
усилия в поперечном сечении стержня (продольная и поперечные силы, крутящий и изгибающие моменты). Напряжение в точке тела (полное, нормальное, касательное). Виды простейших деформаций стержня. Понятие о расчетной схеме. Принцип начальных
размеров. Принцип независимости действия сил. Принцип Сен-Венана.
Растяжение и сжатие прямых стержней
Центральное растяжение или сжатие. Продольная сила. Эпюры продольных сил.
Напряжения в поперечных сечениях стержня. Основные допущения. Эпюра напряжений. Напряжения в сечениях, наклонных к оси стержня. Продольная и поперечная деформации. Закон Гука при растяжении и сжатии. Модуль Юнга. Коэффициент Пуассона. Эпюра перемещений. Жесткость стержня. Потенциальная энергия деформации.
Опытное изучение механических свойств материалов при растяжении и сжатии. Диаграммы растяжения и сжатия пластичных материалов. Основные механические характеристики материала: предел пропорциональности, предел упругости, предел текучести
и предел прочности. Понятие об истинной диаграмме растяжения и сжатия. Разгрузка и
повторное нагружение. Наклеп. Диаграммы растяжения и сжатия хрупких материалов и
основные механические характеристики. Особенности разрушения хрупких материалов
при растяжении и сжатии. Предельное состояние и его критерии в зависимости от
свойств материала, условий работы и назначения конструкции. Расчет по допускаемым
напряжениям и нагрузкам. Коэффициент запаса. Типы задач при расчете на прочность:
проверка на прочность, подбор сечений, определение допускаемой нагрузки. Расчеты
на жесткость. Статически неопределимые системы.
Геометрические характеристики плоских сечений
Статический момент. Определение положения центра тяжести поперечного сечения стержня. Осевой, полярный и центробежный моменты инерции. Осевые моменты
инерции простейших фигур. Изменение моментов инерции при параллельном переносе
и повороте координатных осей. Главные центральные оси. Главные моменты инерции.
Сдвиг и кручение
Напряжения и деформации при чистом сдвиге. Механические свойства материала
при сдвиге. Закон Гука. Модуль сдвига. Связь между модулем сдвига, модулем Юнга и
коэффициентом Пуассона для изотропного тела. Потенциальная энергия деформации.
Исследование напряженного состояния при сдвиге. Главные напряжения и главные
площадки. Понятие о расчете на прочность соединений, работающих на сдвиг. Внешние силы, вызывающие кручение стержня. Эпюры крутящих моментов. Кручение
стержня круглого поперечного сечения. Закон Гука. Угол закручивания. Жесткость при
кручении. Главные напряжения и главные площадки. Виды разрушения при кручении.
1. Рабочая программа
5
Определение напряжений и углов закручивания. Подбор сечения. Вычисление допускаемого крутящего момента из расчета на прочность и жесткость. Потенциальная энергия деформации. Статически неопределимые задачи. Расчет пружин с малым шагом.
Основы кручения стержней прямоугольного поперечного сечения.
Теория напряженного и деформированного состояния
Главные напряжения и главные площадки. Экстремальные значения касательных
напряжений. Компоненты деформации. Обобщенный закон Гука. Удельная потенциальная энергия. Удельная энергия изменения объема и формы.
Плоский изгиб прямых стержней
Внешние силы, вызывающие плоский изгиб. Типы опорных закреплений. Гипотеза плоских сечений. Определение внутренних силовых факторов в поперечных сечениях балки. Эпюры поперечных сил и изгибающих моментов. Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью поперечной нагрузки. Чистый и поперечный изгиб. Закон Гука при чистом изгибе. Жесткость
балки при изгибе. Нормальные напряжения при чистом изгибе. Касательные напряжения при поперечном изгибе. Исследование напряженного состояния балки при изгибе.
Главные напряжения. Наибольшие касательные напряжения. Расчет на прочность. Потенциальная энергия деформации при изгибе.
Определение перемещений балки при плоском изгибе
Дифференциальное уравнение изгиба балки. Точное и приближенное уравнения для
кривизны. Граничные условия. Метод начальных параметров. Энергетические теоремы.
Теоремы о взаимности работ и перемещений. Интеграл Мора. Правило Верещагина
Расчет простейших статически неопределимых балок методом сил
Статически неопределимые балки. Степень статической неопределимости. Лишние неизвестные. Основная система. Уравнения метода сил.
Гипотезы прочности
Назначение гипотез прочности. Понятие об эквивалентном напряжении. Гипотеза
наибольших нормальных напряжений. Гипотеза наибольших деформаций. Гипотеза
наибольших касательных напряжений. Энергетическая гипотеза. Гипотеза разрушения
Мора для материалов с различными пределами прочности при растяжении и сжатии.
Сложное сопротивление
Внутренние усилия и их эпюры для плоских и пространственных ломаных стержней.
Косой изгиб. Внецентренное сжатие (растяжение). Ядро сечения. Изгиб с кручением.
Устойчивость стержней
Понятие об устойчивых и неустойчивых формах равновесия. Критическая нагрузка. Формула Л. Эйлера. Энергетический метод определения критической нагрузки. Понятие о приведенной длине стержня. Пределы применимости формулы Л. Эйлера. Потеря устойчивости при напряжениях за пределом пропорциональности материала.
Формула Ф.С. Ясинского. График критических напряжений в зависимости от гибкости
стержня. Практический метод расчета сжатых стержней по коэффициенту уменьшения
допускаемых напряжений. Дифференциальное уравнение продольно-поперечного изгиба. Приближенный метод расчета.
1. Рабочая программа
6
Расчеты при некоторых видах динамической нагрузки
Силы инерции. Подъем и опускание груза с ускорением. Расчет тонкого быстровращающегося кольца. Коэффициент динамичности. Продольный и поперечный удары.
Приближенный учет массы стержня при падении груза.
Прочность при напряжениях, циклически изменяющихся во времени
Виды циклов и их характеристики. Усталостное разрушение. Сопротивление при
переменных напряжениях. Кривая Велера и предел выносливости. Причины усталостного разрушения. Основные факторы, влияющие на предел выносливости. Диаграммы
предельных напряжений при асимметричных циклах. Выносливость при совместном
кручении и изгибе. Коэффициент запаса прочности при переменных напряжениях.
Расчет оболочек
Безмоментная теория тонкостенных оболочек вращения. Цилиндрическая и сферическая оболочки, находящиеся под действием всестороннего внешнего (внутреннего)
давления.
2. Вопросы для самоконтроля
7
2.1. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
ТЕМА 1: ВВЕДЕНИЕ. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ПОНЯТИЯ
1. Какие основные задачи решаются в сопротивлении материалов?
2. Перечислите основные допущения, принимаемые в курсе сопротивления материалов?
3. Что понимается под сплошностью, однородностью, изотропностью материала?
4. Сформулируйте принцип начальных размеров?
5. В чем заключается принцип независимости действия сил?
6. Расскажите о принципе Сен-Венана.
7. Что называется расчетной схемой конструкции, и чем она отличается от реального объекта?
8. Дайте определение стержня, пластины, оболочки, массивного тела.
9. Какие силы называются внутренними? Внешними? Поверхностными? Объемными?
10. В каких единицах измеряются сосредоточенные силы, моменты, распределенная нагрузка?
11. В чем заключается метод сечений и для чего он применяется?
12. Что называется нормальным и касательным напряжением? В каких единицах
они измеряются?
13. Что называется деформацией? Какая деформация называется упругой? Пластической?
ТЕМА 2: РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМЫХ СТЕРЖНЕЙ
1. Какой вид деформации стержня называется осевым растяжением или сжатием?
2. Что называется абсолютной деформацией? Относительной? В каких единицах
они измеряются?
3. Что происходит с поперечными и продольными размерами стержня при растяжении или сжатии?
4. Как определяется коэффициент поперечной деформации (коэффициент Пуассона)? В каких пределах он изменяется для изотропных материалов?
5. Что называется модулем Юнга? В каких единицах он измеряется?
6. Что называется жесткостью стержня при растяжении (сжатии)?
7. В чем заключается закон Гука для материала и стержня, как конструкции?
8. Как распределяются нормальные напряжения по поперечному сечению
стержня при растяжении (сжатии)?
9. Как вычисляются нормальные и касательные напряжения в наклонном сечении стержня при растяжении (сжатии)?
10. В каких сечениях растянутого стержня возникают наибольшие нормальные
напряжения? Наибольшие касательные напряжения?
11. Как записывается условие прочности при растяжении (сжатии)?
12. Какие три характерные задачи встречаются при расчете на прочность при растяжении (сжатии)?
13. Что называется продольной силой, и как она определяется в произвольном
поперечном сечении стержня?
14. Что представляет собой эпюра продольных сил, и как она строится?
15. Какие сечения стержня считаются опасными?
16. По какой формуле вычисляются нормальные напряжения в поперечном сечении стержня при растяжении (сжатии)?
17. Как определяются продольные деформации?
2. Вопросы для самоконтроля
8
18. Какие системы называются статически неопределимыми? Как определяется
степень их статической неопределимости?
19. Каков общий план решения статически неопределимых задач?
20. Как составить дополнительные уравнения (условия совместности деформаций)?
21. В каких координатах строится диаграмма растяжения?
22. Что называется пределом пропорциональности, пределом упругости, пределом текучести, пределом прочности?
23. Что такое площадка текучести?
24. Каковы отличия диаграмм растяжения пластичного и хрупкого материалов?
25. Как происходит разрушение при растяжении и сжатии пластичных и хрупких
материалов?
26. Что называется остаточным относительным удлинением образца и остаточным относительным сужением шейки образца? Какое свойство материала характеризуют эти величины?
27. Какие материалы называются анизотропными?
28. Чем отличается диаграмма истинных напряжений от диаграммы условных
напряжений?
29. Как определить по диаграмме растяжения упругую и пластическую деформации?
30. Что принимается за предельное напряжение для пластичных материалов? Для
хрупких?
31. Что называется допускаемым напряжением? Как оно вычисляется для пластичных и хрупких материалов? Что называется коэффициентом запаса прочности?
ТЕМА 3: ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
1. Что называется статическим моментом площади сечения относительно оси? В
каких единицах он измеряется? Знак?
2. Чему равен статический момент относительно оси, проходящей через центр
тяжести сечения?
3. Как определить координаты центра тяжести простой (и сложной) плоской фигуры?
4. Что называется осевым, полярным и центробежным моментами инерции сечения? В каких единицах они измеряются? Знак?
5. Как отражается на знаке центробежного момента инерции изменение положительных направлений одной или обеих координатных осей?
6. Чему равны осевые моменты инерции прямоугольника относительно оси,
совпадающей с одной из его сторон, и относительно центральной оси, параллельной одной из его сторон?
7. Чему равны осевой и полярный моменты инерции круга и кольца относительно осей, проходящих через центр тяжести поперечного сечения?
8. Изменится ли сумма осевых моментов инерции относительно двух перпендикулярных осей при повороте этих осей на некоторый угол?
9. Какие оси называются главными центральными осями инерции?
10. Чему равен центробежный момент инерции относительно главных центральных осей инерции?
11. В каких случаях можно без вычисления установить положение главных центральных осей инерции?
ТЕМА 4: СДВИГ И КРУЧЕНИЕ
1. При каком нагружении стержень испытывает сдвиг? Кручение?
2. Как строится эпюра крутящих моментов?
3. Как определяется скручивающий момент по мощности, передаваемой валом,
и по числу оборотов в минуту?
2. Вопросы для самоконтроля
9
4. Какие гипотезы положены в основу теории кручения стержня круглого поперечного сечения?
5. Что называется абсолютным и относительным сдвигом? Углом сдвига?
6. Как формулируется закон Гука при сдвиге для материала?
7. Какие напряжения возникают в поперечном сечении круглого стержня при
кручении? Как они направлены и распределены по сечению?
8. Возникают ли в поперечном сечении нормальные напряжения при кручении
стержня круглого поперечного сечения?
9. Приведите формулу для определения угла закручивания вала.
10. Что называется жесткостью сечения при кручении?
11. Чему равен полярный момент инерции круглого сечения? В каких единицах
он измеряется?
12. Что называется моментом сопротивления при кручении? В каких единицах он
измеряется?
13. Чему равен момент сопротивления кольцевого сечения?
14. Чем объясняется, что стержень кольцевого сечения при кручении более экономичен, чем сплошной?
15. Как разрушаются при кручении стальные и чугунные стержни?
16. Как производится расчет на прочность при кручении?
17. Как выбираются допускаемые напряжения при расчете на прочность при кручении?
18. Как производится расчет на жесткость при кручении?
19. Как вычисляются напряжения в цилиндрической винтовой пружине?
20. Приведите формулу для определения осадки цилиндрической винтовой пружины с малым шагом витков.
21. Остаются ли плоскими при кручении поперечные сечения некруглых стержней?
22. Как вычисляются напряжения при сдвиге (срезе)?
23. Как производится расчет на прочность заклепочных и сварных соединений?
24. В каких единицах измеряется модуль сдвига?
25. Приведите зависимость, связывающую модуль сдвига и модуль Юнга.
ТЕМА 5: ТЕОРИЯ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
Чем характеризуется напряженное состояние в точке тела?
Какое напряженное состояние называется линейным, плоским, объемным?
Сформулируйте правило знаков для компонентов напряжений.
Сформулируйте и выведите условие парности касательных напряжений.
Какие напряжения и площадки называются главными?
По какой формуле вычисляются главные напряжения для случая плоского
напряженного состояния?
7. Как вычисляются наибольшие касательные напряжения для случая плоского
напряженного состояния? В каких площадках они возникают?
1.
2.
3.
4.
5.
6.
ТЕМА 6: ПЛОСКИЙ ИЗГИБ ПРЯМЫХ СТЕРЖНЕЙ
Какой изгиб называется чистым? Плоским?
Какие основные типы опор применяются для закрепления балок?
Какие опорные закрепления может иметь статически определимая балка?
Какие уравнения используются для определения опорных реакций?
Какие внутренние усилия возникают в поперечном сечении балки при плоском изгибе?
6. Приведите правила знаков для изгибающих моментов и поперечных сил.
1.
2.
3.
4.
5.
2. Вопросы для самоконтроля
10
7. Как вычисляются изгибающий момент и поперечная сила в поперечном сечении балки?
8. Выведите дифференциальные зависимости между изгибающим моментом,
поперечной силой и распределенной нагрузкой.
9. Что представляет собой ордината эпюры поперечных сил? Изгибающих моментов?
10. Как осуществляется проверка правильности построения эпюр изгибающих
моментов и поперечных сил?
11. Чему равна поперечная сила в тех сечениях балки, для которых изгибающий
момент достигает экстремального значения?
12. По каким законам изменяются поперечная сила и изгибающий момент по
длине балки при отсутствии распределенной нагрузки?
13. В какую сторону обращена выпуклость эпюры изгибающих моментов при
распределенной нагрузке, направленной вниз?
14. Перечислите основные допущения, положенные в основу вывода формулы
для нормальных напряжений, возникающих в балке при чистом изгибе.
15. Чему равна кривизна оси балки при чистом изгибе?
16. Как записывается закон Гука при изгибе балки?
17. Что называется нейтральной осью при изгибе и как она расположена?
18. По какой формуле вычисляются нормальные напряжения при изгибе балки?
Как они изменяются по высоте и ширине поперечного сечения?
19. Что называется жесткостью при изгибе?
20. Что называется осевым моментом сопротивления при изгибе? В каких единицах он измеряется?
21. Какое сечение имеет больший момент сопротивления при одинаковой площади: круглое или квадратное?
22. В каких поперечных сечениях балки возникают касательные напряжения?
23. Как записывается формула Журавского?
24. Как распределяются касательные напряжения в поперечном сечении балки
прямоугольного, круглого, двутаврового поперечных сечений?
25. Запишите условия прочности балки по нормальным и касательным напряжениям.
ТЕМА 7: ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ БАЛКИ ПРИ ПЛОСКОМ ИЗГИБЕ
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Какие перемещения получают поперечные сечения балки при плоском изгибе?
Запишите дифференциальное уравнение упругой линии балки.
Запишите универсальное уравнение упругой линии балки.
Что называют начальными параметрами?
Как записываются граничные условия для случая шарнирного опирания?
Жесткой заделки?
Как вычисляется потенциальная энергия балки при изгибе?
Сформулируйте теорему о взаимности работ.
Запишите интеграл Мора.
В каком порядке производится определение перемещений балки по формуле Мора?
Как производится «перемножение» эпюр по правилу Верещагина? О чем свидетельствует знак, полученный в результате «перемножения» эпюр?
ТЕМА 8: РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫХ БАЛОК МЕТОДОМ СИЛ
1. Какие балки называются статически неопределимыми?
2. В чем заключается идея метода сил?
3. Какая система называется основной? Как она выбирается?
2. Вопросы для самоконтроля
11
4. Какие неизвестные усилия могут рассматриваться как «лишние»?
5. Как записывается система канонических уравнений метода сил? Чему равно
число уравнений?
6. Что выражает каждое из уравнений системы?
ТЕМА 9: ГИПОТЕЗЫ ПРОЧНОСТИ
1. Какое состояние материала называется опасным? Чем характеризуется
наступление опасного состояния для пластичных и хрупких материалов?
2. Почему вопрос о прочности в условиях объемного напряженного состояния
приходится решать на основе результатов опытов, проводимых при линейном
напряженном состоянии?
3. Что такое гипотезы прочности?
4. Как формулируется первая гипотеза прочности? В каких случаях допустимо
применение этой гипотезы?
5. Как определяется эквивалентное напряжение по второй гипотезе прочности?
Когда она применяется?
6. Что называется эквивалентным напряжением?
7. Зависит ли эквивалентное напряжение по третьей гипотезе прочности от второго
главного напряжения? Укажите недостатки и область применения этой гипотезы.
8. Как формулируется четвертая гипотеза прочности?
9. Какой подход к оценке предельного состояния используется в гипотезе Мора?
10. Как производится полная проверка прочности балки при плоском изгибе?
ТЕМА 10: СЛОЖНОЕ СОПРОТИВЛЕНИЕ
1. Что называется сложным сопротивлением?
2. Что такое косой изгиб? По какой формуле определяются нормальные напряжения при косом изгибе?
3. Как определяется положение нулевой линии?
4. Как определяется положение опасных точек поперечного сечения при косом изгибе?
5. Запишите условие прочности при косом изгибе.
6. Как определяются касательные напряжения при косом изгибе?
7. Как определяются перемещения балки при косом изгибе?
8. Какой случай сложного сопротивления называется внецентренным растяжением (сжатием)?
9. По какой формуле определяются нормальные напряжения при внецентренном
растяжении (сжатии)?
10. Как определяется положение нулевой линии при внецентренном растяжении (сжатии)?
11. Как перемещается нулевая линия при перемещении точки приложения нагрузки?
12. Запишите условие прочности при внецентренном растяжении (сжатии).
13. Что такое ядро сечения? Как оно строится?
14. Может ли при внецентренном растяжении (сжатии) нулевая линия оказаться
за пределами сечения?
15. Какие напряжения возникают в поперечном сечении стержня при изгибе с
кручением?
16. Как найти опасное сечение вала при изгибе с кручением?
17. Какие точки круглого поперечного сечения стержня являются опасными при изгибе с кручением? Какое напряженное состояние имеет место в этих точках?
18. По третьей или четвертой гипотезе прочности получается большая величина
расчетного момента?
2. Вопросы для самоконтроля
12
ТЕМА 11: УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
1. Что понимается под устойчивостью стержня? Какая сила называется критической?
2. Перечислите и дайте характеристику видов равновесия стержня.
3. Какое дифференциальное уравнение, и какие допущения лежат в основе вывода формулы Эйлера?
4. Что называется гибкостью стержня?
5. Чему равна Эйлерова сила для шарнирно опертого по концам стержня?
6. Какие параметры влияют на величину Эйлеровой нагрузки?
7. Что такое коэффициент приведения длины стержня? Чему он равен для некоторых случаев закрепления концов стержня?
8. Каковы пределы применимости формулы Эйлера?
9. Как определяется предельная гибкость стержня?
10. Какое отличие между Эйлеровой и критической нагрузками?
11. Как определяется критическая нагрузка по формуле Ясинского?
12. Приведите график критических напряжений.
13. Что такое коэффициент уменьшения основного допускаемого напряжения? От
чего зависит его величина, и в каких пределах она изменяется?
14. Как производится подбор поперечного сечения сжатой стойки?
ТЕМА 12: РАСЧЕТЫ ПРИ НЕКОТОРЫХ ВИДАХ ДИНАМИЧЕСКОЙ НАГРУЗКИ
1.
2.
3.
4.
5.
6.
7.
Реальными или фиктивными нагрузками являются силы инерции?
Какие нагрузки считаются статическими, а какие динамическими?
Как вычисляются напряжения в тросе при ускоренном поднятии (опускании) груза?
Что такое коэффициент динамичности?
Чему равен коэффициент динамичности при ударе?
Каким образом можно уменьшить значение коэффициента динамичности при ударе?
Зависят ли напряжения при ударе от модуля Юнга материала?
ТЕМА 13: ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ, ЦИКЛИЧЕСКИ
ИЗМЕНЯЮЩИХСЯ ВО ВРЕМЕНИ
1. Что называется циклом напряжений? Что называется максимальным, минимальным, средним напряжением, амплитудой, коэффициентом асимметрии цикла?
2. Какой цикл называется симметричным? Отнулевым? Асимметричным? Постоянным?
3. Какой цикл называется знакопостоянным? Знакопеременным?
4. Какой цикл называется предельным?
5. Что называется усталостью? Каков характер усталостных разрушений?
6. Как выглядит кривая Велера, и как ее получают?
7. Что такое предел выносливости? Что такое базовое число циклов?
8. Какие основные факторы влияют на величину предела выносливости?
9. Какова зависимость предела выносливости от коэффициента асимметрии цикла?
10. Приведите варианты схематизации диаграммы предельных циклов.
ТЕМА 14: РАСЧЕТ ОБОЛОЧЕК
1. Какое напряженное состояние оболочки называется безмоментным?
2. По каким формулам вычисляются напряжения в вытянутой цилиндрической
оболочке, нагруженной равномерным всесторонним внешним давлением?
3. По каким формулам вычисляются нормальные напряжения в сферической
оболочке, нагруженной равномерным всесторонним внешним давлением?
3. Темы, варианты и примеры решения задач
3.
13
ТЕМЫ, ВАРИАНТЫ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Учебной программой дисциплины предусматривается выполнение самостоятельной работы с индивидуальными заданиями для каждого студента. Содержание и количество задач для самостоятельной работы устанавливается преподавателем.
Вариант задания вы определяете по первым буквам своей фамилии, имени и отчества по таблицам, приведенным к каждой задаче.
Эти таблицы составлены следующим образом. Первый столбец содержит буквы
алфавита. Во втором столбце указаны номера схем по соответствующему рисунку. В
остальных столбцах приводятся исходные данные, необходимые для решения задачи.
Против начальной буквы своей фамилии по горизонтали из второго столбца
определяете номер схемы. Числовые данные к принятой схеме выбираете также по горизонтали следующим образом: против начальной буквы своего имени из нечетных
столбцов, а против начальной буквы своего отчества из четных столбцов.
3.1. РАСТЯЖЕНИЕ И СЖАТИЕ
Задача 1
Стальной стержень (модуль Юнга E  2104 кН/см2) находится под действием
внешних осевых сил P и 2 P (рис. 3.1). Построить эпюры продольных сил N и нормальных напряжений  z . Оценить прочность стержня, если допускаемое напряжение
   21 кН/ см2. Найти удлинение стержня l . Данные взять из табл. 3.1.
Таблица 3.1
Исходные данные к задаче 1
Начальная буква фамилии,
имени, отчества
1
А, П
Б, Р
В, С
Г, Т
Д, У
Е, Ф
Ж, Х
З, Ц
И, Ч
К, Ш
Л, Щ
М, Э
Н, Ю
О, Я
Номер схемы
(рис. 3.1)
2
1
2
3
4
5
6
7
8
9
0
1
2
3
4
F, см2
a, м
b, м
c, м
P, кН
3
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
2,2
2,4
2,6
2,8
4
1,2
1,4
1,8
1,6
2,0
2,2
2,4
2,6
2,8
2,4
1,6
1,6
2,0
1,8
5
1,4
1,6
1,6
2,0
1,8
1,6
1,4
1,2
1,0
1,6
1,4
1,8
1,8
2,0
6
1,6
1,4
1,2
1,0
1,2
1,4
1,6
1,8
1,4
1,2
1,2
1,0
1,0
1,4
7
11
12
13
14
15
16
17
18
19
20
10
11
13
14
Пример 1
Стальной стержень (модуль Юнга E  2104 кН/см2) с размерами a  200 см;
b  150 см, c  100 см и площадью поперечного сечения нижнего участка F  10 см2, а
верхнего – 2F  20 см2 нагружен внешними осевыми силами P1  100 кН и P2  300
кН (рис. 3.2). Построить эпюры продольных сил N и нормальных напряжений  z .
Оценить прочность стержня, если допускаемое напряжение    21 кН/см2. Найти
удлинение стержня l .
3. Темы, варианты и примеры решения задач
14
Решение
1. Определяем опорную реакцию R .
Учитывая, что P2  P1 , направим опорную реакцию R вниз. Тогда из уравнения
равновесия  Z  0 находим:
 R  P2  P1  0;
R  P2  P1 ;
R  300  100  200 кН.
3
2
F
4
5
F
F
c
1
2Р
2F
2F
2Р
2Р
b
Р
Р
2Р
8
0
9
2F
Р
F
Р
2F
2F
2Р
F
F
2Р
2Р
Р
Р
c
7
6
Р
Р
b
Р
2Р
F
Р
a
2Р
F
a
2F
2Р
Рис. 3.1
2. Строим эпюру продольных сил N .
Разбиваем длину стержня на три участка (рис. 3.2, а). Границами участков являются те сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений (РОЗУ). Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Начнем с сечения 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть
стержня (рис. 3.2, б). Видим, что внешняя сила P1 растягивает рассматриваемую часть
стержня. Очевидно, что отброшенная часть противодействует растяжению. Это противодействие отброшенной части мы заменим внутренней продольной силой N1 . Раз-
3. Темы, варианты и примеры решения задач
15
рушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1
сила N1 сможет уравновесить силу P1 . Поэтому
N1  P1  100 кН.
Переходим к сечению 2 – 2 (рис. 3.2, в). Внешняя сила P1 растягивает рассматриваемую часть стержня, а сила P2 ее сжимает. Причем, согласно условию, P2  P1 . Чтобы уравновесить эти две силы в сечении 2 – 2 должна возникнуть внутренняя сила,
противодействующая сжатию и равная
N2  P2  P1 ;
N 2  300  100  200 кН.
R = 200 кН
N кН
г)
3
c=2,0 м
3
R
2F = 20 см 2
σ
200
10
N3
a = 1,0 м
b = 1,5 м
N2
2
20
2
P2 = 300 кН
200
20
100
1
F = 10 см
10
P2
N1
1
кН/см 2
10
2
100
P1 = 100 кН
а)
P1
б)
10
Р1
в)
д)
е)
Рис. 3.2
Переходим к сечению 3 – 3 (рис. 3.2, г). Теперь мы отбросим часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила N 3 должна уравновесить внешнюю (реактивную) сжимающую силу R , поэтому она будет равна:
N 3  R  200 кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим верхнюю часть стержня.
При построении эпюры продольных сил N будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении
стержня, считается положительной, если она противодействует растяжению
стержня, и отрицательной, если она противодействует его сжатию. Это правило
знаков вводится для того, чтобы наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна N1  100 . В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому
N 2  N 3  200 кН.
3. Темы, варианты и примеры решения задач
16
Для построения эпюры продольных сил N проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой оси. В пределах каждого из
участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Каждая линия «штриховки» (ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Отметим, что в местах приложения внешних сил на эпюре N мы получили скачкообразное изменение продольной силы на величину соответствующей внешней силы.
Изменение поперечного размера стержня, как видно из рис. 3.2, д, никак не сказалось
на эпюре N .
3. Строим эпюру нормальных напряжений (  z ).
Нормальное напряжение при растяжении (сжатии) вычисляется по формуле:
z  N F ,
где N – продольное усилие, возникающее в данном поперечном сечении стержня, а F –
площадь этого поперечного сечения.
Нормальные напряжения в поперечных сечениях стержня равны:
в первом
N
100
z  1 ;
z  
 10 кН/см2;
F
10
во втором
N
200
z  2 ;
z  
 20 кН/см2;
F
10
в третьем
N
200
z  3 ;
z  
 10 кН/см2.
2F
20
Строим по вычисленным значениям эпюру  z (рис. 3.2, е). В пределах каждого из
участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси.
Заметим, что в отличие от эпюры N, на эпюре  z «скачки» имеют место не только в
местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
4. Оцениваем прочность стержня.
Сопоставляем наибольшее нормальное напряжение, возникающее во втором сечении стержня с допускаемым напряжением (знак напряжения, характеризующий только
вид деформации, не учитываем):
 zmax   z2  20 кН/см2;
1
1
2
2
3
3
20 кН/см2 <    21 кН/см2.
Следовательно, прочность стержня обеспечена.
5. Вычисляем удлинение всего стержня ( l ).
При ступенчато-переменных по длине стержня значениях продольной силы и
площади поперечного сечения удлинение стержня вычисляется по формуле:
N l
l   k k ,
k EFk
где k – номер участка, а N k , lk , Fk – соответственно, продольная сила, длина и площадь
поперечного сечения; E – модуль Юнга.
Тогда
3. Темы, варианты и примеры решения задач
17
N1l1 N 2 l 2 N 3l3
;


EF1 EF2
EF3
100 100 200 150 200  200


 0,2 см.
l 
2 10 4 10 2 10 4 10 2 10 4  20
Полученный результат означает, что длина стержня уменьшилась на 2 мм.
l 
3.2. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
ПРИ РАСТЯЖЕНИИ И СЖАТИИ
Задача 2
1
c
P
lм
lст
P
lм
c
lст
Горизонтальный абсолютно жесткий на изгиб брус (рис. 3.3), нагруженный силой
P, опирается на шарнирно неподвижную опору и поддерживается двумя упругими
стержнями, прикрепленными к нему и к основанию с помощью шарниров. Один из
стержней стальной  E ст  2  10 4 кН/см2;  ст  16 кН/см2  , а другой медный
 E м  1 10 4 кН/см2;  м  8 кН/см2  . Требуется определить усилия и напряжения в
стержнях, выразив их через силу P , а также найти допускаемую нагрузку P .
Данные взять из табл. 3.2.
2
a
b
c
lст
c
P
b
lм
a
P
4
a
c
lст
lст
P
b
lм
c
b
lст
a
lм
3
P
6
a
b
a
lм
5
b
Рис. 3.3
Таблица 3.2
Исходные данные к задаче 2
Начальная буква фамилии, Номер схемы
Fст, см2 Fм, см2
имени, отчества
(рис. 3.2)
1
2
3
4
А, П
1
1,0
2,0
Б, Р
2
1,0
2,0
В, С
3
2,0
4,0
lст, м
lм, м
a, м
b, м
c, м
5
1,0
1,0
1,0
6
1,0
0,8
1,0
7
1,0
1,0
1,0
8
1,0
0,8
1,0
9
0,5
0,6
1,2
3. Темы, варианты и примеры решения задач
18
Продолжение таблицы 3.2
Начальная буква фамилии, Номер схемы
Fст,, см2 Fм, см2
имени, отчества
(рис. 3.2)
1
2
3
4
Г, Т
4
3,0
5,0
Д, У
5
4,0
6,0
Е, Ф
6
2,0
4,0
Ж, Х
1
2,0
3,0
З, Ц
2
3,0
4,0
И, Ч
3
4,0
5,0
К, Ш
4
5,0
6,0
Л, Щ
5
3,0
4,0
М, Э
6
3,0
5,0
Н, Ю
1
4,0
5,0
О, Я
2
5,0
7,0
lст, м
lм, м
a, м
b, м
c, м
5
1,6
1,8
1,2
1,2
1,0
1,8
2,0
1,4
1,4
1,2
2,0
6
1,4
1,4
1,2
1,0
1,0
1,6
1,6
1,4
1,0
1,2
1,8
7
1,6
1,8
1,2
1,2
1,0
1,8
2,0
1,4
1,4
1,2
2,0
8
1,4
1,4
1,2
1,0
1,0
1,6
1,6
1,4
1,0
1,2
1,8
9
1,0
1,0
0,6
0,8
1,4
1,2
1,2
0,7
0,8
1,6
1,4
Пример 2
Для статически неопределимой системы, изображенной на рис. 3.4, а требуется
определить усилия и напряжения в стальном ( Eст  210 4 кН/см2;  ст  16 кН/ см2) и
в медном ( E м  110 4 кН/см2;  м  8 кН/см2) стержнях, выразив их через силу P, а
также найти допускаемую нагрузку P .Дано: Fcт  3 см2; Fм  6 см2; lст  2,0 м;
l м  1,6 м; a  1,6 м; b  2,0 м, c  2,4 м.
Rст
a)
Rм
A
a = 1,6 м
b)
P
B
Nст = Rст
RА
C
A
b = 2,0 м
a
B
B1
Δlст
c = 2,4 м
Nм = Rм
Δlм
Fм = 6,0 см 2
lст=2,0 м
RА
lм=1,6 м
Fст = 3,0 см 2
C
C1
a+b
Рис. 3.4
Решение
1. Находим усилия и напряжения, возникающие в стержнях.
Рассечем стержни и изобразим систему в деформированном состоянии
(рис. 3.4, б). Под действием силы P абсолютно жесткий на изгиб брус слегка повернется, оставаясь прямолинейным. Деформированное положение системы показано на этом
рисунке штриховыми линиями. Очевидно, что оба стержня, поддерживающие брус,
растянутся. Поэтому внутренние усилия N м и N ст , возникающие в поперечных сечениях стержней, направим от сечения. Удлинение медного стержня ( l м ) равно отрезку
BB1 , а стального ( lст ) – отрезку DD1 .
3. Темы, варианты и примеры решения задач
19
Для плоской системы параллельных сил мы имеем два независимых уравнения
статики. Неизвестных же у нас три: R A , N м и N ст . Следовательно, заданная система
является один раз статически неопределимой.
Чтобы исключить из дальнейшего рассмотрения опорную реакцию R A , возникающую в шарнире A, составим следующее уравнение равновесия:
 M A  0; N м  a  N ст  (a  b)  P  c  0 .
Подставляя в это уравнение значения a и b, получим:
(3.1)
1,6 N м  3,6 N ст  2,4 P .
В уравнение (3.1) входят две неизвестные N м и N ст , поэтому для их определения
(для раскрытия статической неопределимости) нам необходимо составить еще одно,
дополнительное уравнение.
Очевидно, что удлинения стержней l м и lст связаны между собой. Из подобия
треугольников ABB1 и ADD1 следует, что
BB1 l м
a
,


DD1 lст a  b
или, учитывая закон Гука,
N мl м
E м Fм
a
.
(3.2)

N стlст a  b
Eст Fст
Полученное нами уравнение (3.2), связывающее деформации стержней, называется уравнением совместности деформаций.
Подставив в уравнение (3.2) исходные данные задачи и выполнив несложные
преобразования, получим дополнительное к уравнению (3.1) уравнение, связывающее
неизвестные внутренние усилия N м и N ст :
1,8 N м  N ст .
(3.3)
Решая систему уравнений (3.1) и (3.3), найдем, что усилия в стержнях равны:
N м  0,297 P; N ст  0,535P .
Тогда напряжения будут равны:
N
N
0,297 P
0,535P
м  м 
 0,0495P;  ст  ст 
 0,178P .
Fм
6
Fст
3
2. Определяем допускаемую нагрузку P .
Из условия прочности медного стержня  м  0,0495P   м  8 кН/см2 следует, что
8
P
 162 кН.
0,0495
Из условия прочности стального стержня  ст  0,178P   м  16 кН/см2:
16
P
 89,9 кН.
0,178
Принимая меньшее из найденных выше двух значений, находим, что допускаемая
нагрузка для заданной системы равна:
P  89,9 кН.
3. Темы, варианты и примеры решения задач
20
3.3. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ ТЕЛА
Задача 3
τzy
σy
σz
=τyz
τzy
σy
Рис. 3.5
Из нагруженного тела, находящегося в равновесии, выделен элементарный параллелепипед со сторонами dx , dy и dz . Считается, что на двух его параллельных гранях с нормалью x нормальные (  x ) и касаσz тельные (  xy ,  xz ) напряжения отсутствуют, то есть
напряженное состояние является плоским. Вместо объемного параллелепипеда с целью упрощения на рисунке
τyz
3.5 показан плоский элемент: его проекция на плоскость
yz . Штриховкой указана внутренняя область элемента.
Требуется найти главные напряжения  1   2   3 ,
направления главных площадок и максимальное касательное напряжение (  max ). Данные взять из табл. 3.3.
Таблица 3.3
Исходные данные к задаче 3
Начальная буква фамилии, имени,
отчества
1
А, П
Б, Р
В, С
Г, Т
Д, У
Е, Ф
Ж, Х
З, Ц
И, Ч
К, Ш
Л, Щ
М, Э
Н, Ю
О, Я
 z , кН/см2
 y , кН/см2
 yz   zy , кН/см2
2
10
2
3
4
5
6
7
-7
-6
-5
-4
-3
-2
-10
3
6
-7
6
-5
4
3
2
-1
-2
3
4
5
6
7
4
-3
7
-6
5
-4
3
-2
1
-7
6
-5
4
-3
2
Пример 3
Дано  z  12 кН/см2,  y  4 кН/см2,  yz   zy  6 кН/см2 (рис. 3.6, а). Найти
главные напряжения  1   2   3 , направления главных площадок и максимальное касательное напряжение  max .
Решение
Напомним правила знаков для нормальных и касательных напряжений:
1) нормальное напряжение, соответствующее растяжению, считается положительным, а сжатию – отрицательным;
2) касательное напряжение считается положительным, если одновременно выполняются (или одновременно не выполняются) следующие два условия:
 направление напряжения совпадает с положительным направлением соответствующей координатной оси;
3. Темы, варианты и примеры решения задач
21
 внешняя нормаль к площадке, на которой оно возникает, направлена в ту
же сторону, что и другая, соответствующая, координатная ось.
1. Определяем главные напряжения.
Для плоского напряженного состояния одно из главных напряжений равно нулю.
Вычисляем значения двух других главных напряжений:
1
 1   z   y   z   y 2  4 yz2  ;

2
1
 1  12  (4)  12  (4)2  4  (6) 2  14 кН/см2;
2
1
 2    z   y   z   y 2  4 yz2  ;

2
1
 2   12  (4)  12  (4)2  4  (6) 2  6 кН/см2.
2
Учитывая, что  1   2   3 , окончательно, имеем:
 3  6 кН/см2.
 1  14 кН/см2;
 2  0;




σy= -4 кН/см 2
τzy
а)
б)
τyz= -6 кН/см 2
σz
σ3 = -6 кН/см 2
α0 = -18,5º
σ1
σz= 12 кН/см 2
τyz
σ1 = 14 кН/см 2
τzy
σ3
σy
Рис. 3.6
2. Делаем проверку. Должно выполняться следующее условие:
1   2   3   x   y   z ,
14  0  (6)  0  (4)  12
или
8  8,
то есть верно.
3. Находим положение главных площадок.
Углы  0 и  0  90 , определяющие положение двух взаимно перпендикулярных
площадок, на которых возникают главные напряжения  1 и  3 определяются из формулы:
2 yz
2  (6)
tg 2 0 
;
tg 2 0 
 0,75 .
 z  y
12  (4)
Отсюда:  0  18,5 и  0  90  18,5  90  71,5 .
Напомним, что угол  0 считается отрицательным, если он отсчитывается от горизонтальной оси по ходу часовой стрелки.
Найденные углы определяют и направления «действия» главных напряжений  1
и  3 (см. рис. 3.6, б).
3. Темы, варианты и примеры решения задач
22
4. Определяем наибольшее касательное напряжение, возникающее в рассматриваемой точке тела:
14  (6)
 
 10 кН/см2.
 max  1 3 ;
 max 
2
2
3.4. КРУЧЕНИЕ КРУГЛОГО ВАЛА
Задача 4
Жестко защемленный одним концом стальной стержень (модуль сдвига
G  0,8 10 4 кН/см2) круглого поперечного сечения скручивается четырьмя моментами
M i (рис. 3.7).
Требуется:
 построить эпюру крутящих моментов;
 при заданном допускаемом касательном напряжении    8 кН/см2 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35,49, 45, 50, 60, 70, 80, 90, 100, 200 мм;
 построить эпюру углов закручивания поперечных сечений стержня.
Данные взять из табл. 3.4.
М1
М2
М3
М4
М1
М2
М3
М4
М1
М2
М3
М4
М1
М2
М3
М4
М1
М2
М3
М4
М1
М2
М3
М4
b
c
2
1
М1
М2
М3
М4
3
4
М1
М2
М3
М4
5
6
М1
М2
М3
М4
8
7
М1
М2
М3
9
М4
0
a
b
c
d
a
Рис. 3.7
d
3. Темы, варианты и примеры решения задач
23
Таблица 3.4
Исходные данные к задаче
Начальная буква фамилии, Номер схемы
имени, отчества
(рис. 3.7)
1
2
А, П
1
Б, Р
2
В, С
3
Г, Т
4
Д, У
5
Е, Ф
6
Ж, Х
7
З, Ц
8
И, Ч
9
К, Ш
0
Л, Щ
1
М, Э
2
Н, Ю
3
О, Я
4
М1,
кН·м
3
1,0
1,0
2,0
3,0
4,0
2,0
2,0
3,0
4,0
5,0
3,0
3,0
4,0
5,0
М2,
кН·м
4
2,0
2,0
4,0
5,0
6,0
4,0
3,0
4,0
5,0
6,0
4,0
5,0
5,0
7,0
М3,
кН·м
5
1,0
1,0
1,0
1,6
1,8
1,2
1,2
1,0
1,8
2,0
1,4
1,4
1,2
2,0
М4,
кН·м
6
1,0
0,8
1,0
1,4
1,4
1,2
1,0
1,0
1,6
1,6
1,4
1,0
1,2
1,8
a,
м
7
1,0
1,2
1,4
1,6
1,1
1,3
1,5
1,7
1,9
1,2
1,4
1,6
1,8
2,0
b,
м
8
1,2
1,4
1,6
1,0
1,1
1,3
1,5
1,7
1,9
1,4
1,2
1,4
1,6
1,8
c,
м
9
1,4
1,6
1,0
1,2
1,8
1,5
1,3
1,5
1,7
1,4
1,2
1,4
1,6
1,8
d,
м
10
1,6
1,9
1,2
1,4
1,5
1,1
1,3
1,4
1,3
1,2
1,4
1,6
1,8
2,0
Пример 4
К стальному валу постоянного поперечного сечения (рис. 3.8, а) приложены четыре внешних скручивающих момента: M1  1,5 кН·м; M 2  5,5 кН·м; M 3  3,2 кН·м;
M 4  1,8 кН·м. Длины участков стержня: a  1,5 м; b  2 м, c  1 м, d  1,2 м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при    8 кН/см2 и
построить эпюру углов закручивания поперечных сечений стержня.
Решение
1. Определяем реактивный момент, возникающий в жесткой заделке.
Направим его против хода часовой стрелки (при взгляде навстречу оси z). Запишем уравнение равновесия вала. Пользуемся следующим правилом знаков: внешние
моменты (скручивающие, а также реактивный), вращающие вал при взгляде навстречу
оси z против хода часовой стрелки, считаем положительными. Тогда
 M z  0; M A  M1  M 2  M 3  M 4  0;
M A  M1  M 2  M 3  M 4 ;
М А  1,5  5,5  3,2  1,8  2 кН·м.
Знак «плюс» в полученном выражении говорит о том, что мы угадали направление реактивного момента, возникающего в заделке.
2. Строим эпюру крутящих моментов.
Напомним, что внутренний крутящий момент M z , возникающий в некотором поперечном сечении стержня равен алгебраической сумме внешних моментов, приложенных к любой из рассматриваемых частей стержня (действующих левее или правее сделанного сечения).
При построении эпюры крутящих моментов используем следующее правило знаков: внешний момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент (который, в свою очередь, противодействуя этому внешнему
моменту, будет направлен по ходу часовой стрелки).
Разбиваем длину стержня на четыре участка (рис. 3.8, а). Границами участков являются те сечения, в которых приложены внешние моменты. Делаем по одному сечению в произвольном месте каждого из четырех участков стержня.
3. Темы, варианты и примеры решения задач
24
Начнем с сечения 1 – 1. Отбросим (или закроем листком бумаги) левую часть
стержня. Чтобы уравновесить скручивающий момент M 4  1,8 кН·м в поперечном сечении стержня должен возникнуть равный ему и противоположно направленный крутящий момент. С учетом правила знаков
M z1  1,8 кН·м.
По аналогии для сечений 2 – 2 и 3 – 3 находим:
M z 2  M 4  M 3 ;
M z 2  1,8  3,2  5 кН·м;
M z3  M 4  M 3  M 2 ;
M z 3  1,8  3,2  5,5  0,5 кН·м;
Чтобы определить крутящий момент в сечении 4 – 4 отбросим правую часть. Тогда получим:
M z 4  M A  2 кН·м.
МА = 2 кН∙м
кН∙м
кН∙м
кН∙м
A
кН∙м
кН∙м
4
кН∙м
кН∙м
кН∙м
4 кН∙м
B
a = 1,5 м
б)
М3 = 3,2 кН∙м
М1 = 1,5 кН∙м
а)
2,0
М2 = 5,5 кН∙м
3
км
3
C
b=2м
М4 = 1,8 кН∙м
2
1
2 D
1
c = 1м
E
d = 1,2 м
2,0
0,5
0,5
МZ кН∙м
1,8
1,8
5,0 5,0
0,0156
0,0208
в)
φ
рад
0,0052
0,0165
Рис. 3.8
Для построения эпюры крутящих моментов M z проводим тонкой линией ось, параллельную оси стержня z (рис. 3.8, б). Вычисленные значения крутящих моментов в выбранном масштабе и с учетом их знака откладываем от этой оси. В пределах каждого из участков
стержня крутящий момент постоянен, поэтому мы как бы «заштриховываем» вертикальными линиями соответствующий участок. Напомним, что каждая линия «штриховки» (ордина-
3. Темы, варианты и примеры решения задач
25
та эпюры) дает в принятом масштабе значение крутящего момента в соответствующем поперечном сечении стержня. Полученную эпюру обводим жирной линией.
Отметим, что в местах приложения внешних моментов на эпюре M z мы получили скачкообразное изменение внутреннего крутящего момента на величину соответствующего внешнего момента.
3. Определяем диаметр вала из условия прочности.
Условие прочности при кручении имеет вид:
M z max
 max 
   ,
W
где W  d 3 16  0,2d 3 – полярный момент сопротивления (момент сопротивления
при кручении).
Наибольший по абсолютному значению крутящий момент возникает на третьем
участке вала:
M z max  M z 3  500 кН·см.
Тогда требуемый диаметр вала определяется по формуле:
M z3
500
 6,79 см.
0,2  8
0,2 
Округляя полученное значение до стандартного, принимаем диаметр вала равным
d  70 мм.
4. Определяем углы закручивания поперечных сечений A, B, C, D, E и F и строим эпюру углов закручивания.
Сначала вычисляем крутильную жесткость стержня GI  , где I   d 4 32  0,1d 4 –
полярный момент инерции:
GI   0,8 10 4  0,1 7 4  192 10 4 кН·см2.
Углы закручивания на отдельных участках стержня равны:
200  150
M a
 AB 
 0,0156 рад;
 AB  z 4 ;
192  10 4
GI 
d треб  3
;
d треб  3
50  200
M z 3b
 BС 
 0,0052 рад;
;
192  10 4
GI 
 500  100
M c
 CD 
 0,0260 рад;
CD  z 2 ;
192  10 4
GI 
 180  120
M d
 DE 
 0,0113 рад.
 DE  z1 ;
192  10 4
GI 
Угол закручивания сечения A (жесткой заделки)  A  0 . Тогда
B   A   AB ;
 B  0  0,0156  0,0156 рад;
C   B   BC ;
 C  0,0156  0,0052  0,0208 рад;
 D  C  CD ;
 D  0,0208  0,0260  0,0052 рад;
E  D  DE ;
 E  0,0052  0,0113  0,0165 рад.
Эпюра углов закручивания показана на рис. 3.8, в. Отметим, что в пределах длины
каждого из участков стержня угол закручивания изменяется по линейному закону.
 BС 
3. Темы, варианты и примеры решения задач
26
3.5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Задача 5
Для заданного поперечного сечения стержня (рис. 3.9), состоящего из двух прокатных профилей и полосы, требуется найти положение центра тяжести сечения,
направление главных центральных осей инерции u и v, а также вычислить главные центральные моменты инерции I max и I min . Данные взять из табл. 3.5.
2
1
4
7
3
5
8
6
0
9
Рис. 3.9
Таблица 3.5
Исходные данные к задаче 5
Начальная буква фамилии, Номер схемы
имени, отчества
(рис. 3.9)
1
2
А, П
1
Б, Р
2
В, С
3
Г, Т
4
Д, У
5
Е, Ф
6
Номер
швеллера
3
24
22
20
18
16
14
Номер
двутавра
4
12
14
16
18
20
22
Размеры
уголка
5
100×100×8
100×100×10
100×100×12
100×100×8
100×100×10
100×100×12
Толщина
листа, мм
7
12
12
12
14
14
14
3. Темы, варианты и примеры решения задач
27
Продолжение табл. 3.5
Начальная буква фамилии, Номер схемы
имени, отчества
(рис. 3.9)
1
2
Ж, Х
7
З, Ц
8
И, Ч
9
К, Ш
0
Л, Щ
1
М, Э
2
Н, Ю
3
О, Я
4
Номер
швеллера
3
12
24
22
20
18
16
14
12
Номер
двутавра
4
24
22
20
18
16
14
12
10
Размеры
уголка
5
100×100×8
100×100×10
100×100×12
100×100×8
100×100×10
100×100×12
100×100×8
100×100×10
Толщина
листа, мм
7
16
16
16
10
10
10
14
14
Пример 5
Для составного поперечного сечения стержня, состоящего из равнобокого уголка
№ 7 с толщиной стенки равной 8 мм (ГОСТ 8509 – 93), швеллера № 22 (ГОСТ 8240 –
89) и полосы 180  20 мм (рис. 3.10), требуется найти положение центра тяжести сечения, направление главных центральных осей инерции u и v, а также вычислить главные
центральные моменты инерции I max и I min .
Решение
1. Определяем координаты центра тяжести поперечного сечения.
Размеры и геометрические характеристики уголка и швеллера устанавливаем по
сортаментам. Вычерчиваем сечение в масштабе (рис. 3.11). Выбираем оси сравнения x
и y , располагая их по контуру швеллера. Именно в этих осях мы и будем определять
положение центра тяжести всего сечения. Для каждого элемента сечения (уголка,
швеллера и полосы) проводим собственные центральные оси xi , yi ( i  1, 2, 3 ), параллельные выбранным осям сравнения x и y .
Координаты центра тяжести всего поперечного сечения (точка С), состоящего из
трех элементов (уголка – 1, швеллера – 2 и полосы – 3), вычисляются по формулам:
S y S y1  S y 2  S y 3 F1 x1  F2 x2  F3 x3
xc 


;
F
F1  F2  F3
F1  F2  F3
S x S x1  S x 2  S x 3 F1 y1  F2 y 2  F3 y3


,
F
F1  F2  F3
F1  F2  F3
– статические моменты соответствующего элемента относительно осей
yc 
где S yi и S xi
сравнения; Fi – площадь элемента; xi и yi – координаты центра тяжести элемента Ci в
осях сравнения. Вычисления производим в табличной форме (табл. 3.6).
Таблица 3.6
Определение координат центра тяжести поперечного сечения
Номер
элемента
Наименование
элемента
Координаты центра
Площадь
элемента тяжести элемента C i , см
Fi , см2
x
y
i
1
2
3

Уголок
Швеллер
Полоса
Все сечение
10,67
26,70
36,00
73,37
-2,02
2,21
9,00
i
17,02
11,00
-1,00
Статические моменты элемента
относительно осей сравнения, см3
S yi  Fi xi
S xi  Fi yi
-21,55
59,01
324,00
361,46
181,60
293,70
-36,00
439,30
3. Темы, варианты и примеры решения задач
28
V (min)
Y0
Y
Y1
Y3
x1 = -2,02 см
x2 = 2,21 см
Уголок 70х70х8
Швеллер № 22
X1
1
•
U (max)
y2 = -1,0 см
y01
X2
αо = 25,9º
y02
2•
С
Х0
y03
•
yC = 5,99 см
y2=11,0 см
y1 = 17,02 см
x01
Y3
0
•
x02
X
3
X3
Полоса 180 х 20
x03
xC = 4,93 см
x3 = 9,0 см
Рис. 3.11
Координаты центра тяжести поперечного сечения (точка С) в осях x , y :
Sy
361,46
xc 
;
xc 
 4,93 см;
73,37
F
S
439,30
yc  x ;
yc 
 5,99 см.
F
73,37
По найденным значениям xс и y с отмечаем на чертеже центр тяжести всего сечения точку С (см. рис. 3.11) и проводим центральные оси x0 и y0 .
Заметим, что центр тяжести всей фигуры должен располагаться внутри треугольника, вершинами которого являются центры тяжести элементов поперечного сечения.
2. Вычисляем моменты инерции всего поперечного сечения относительно центральных осей x0 и y0 .
Осевые и центробежный моменты инерции сечения относительно центральных
осей определяются по следующим формулам:
2
2
2
I x  I x  y01
F1  I x  y02
F2  I x  y03
F3 ;
0
Iy
0

 I
1
y1
x
 
F  I
2
01 1
2
y2
x
 
F  I
2
02 2
3
y3
x

F ;
2
03 3
3. Темы, варианты и примеры решения задач

 
29
 

I x y  I x y  x01 y 01 F1  I x y  x02 y 02 F2  I x y  x03 y 03 F3 .
0
0
1 1
2
2
3
3
Значения осевых моментов инерции уголка ( I x1 , I y1 ) и швеллера ( I x2 , I y2 ) относительно собственных центральных осей xi и yi определяем по сортаменту. Для полосы осевые моменты инерции, соответственно, равны:
18  23
183  2
I x3 
 12 см4;
I y3 
 972 см4.
12
12
Центробежные моменты инерции швеллера ( I x2 y2 ) и полосы ( I x3 y3 ) равны нулю,
поскольку их собственные центральные оси являются осями симметрии.
Центробежный момент инерции уголка ( I x1 y1 ) относительно собственных центральных осей x1 и y1 вычисляется по формуле:
1
I x1 y1   I max  I min  ,
2
где I max и I min – максимальный и минимальный главные моменты инерции уголка, соответственно.
По сортаменту находим, что
а
I max  76,35 см4,
I min  19,97 см4.
Центробежный момент инерции уголка не равен нулю, поскольку оси x1 и y1 не
являются для него главными центральными осями инерции (главные центральные оси
для равнобокого уголка повернуты относительно осей x1 и y1 на угол 45º).
Знак центробежного момента инерции уголка (как, впрочем, и для любой другой
фигуры) зависит от направления координатных осей. Он легко определяется следующим образом. По определению, центробежный момент инерции фигуры равен интегралу произведения элементарных площадок на их расстояния до координатных осей.
Мысленно разделим уголок на три площади, расположенные, в нашем случае, в
первом, третьем и четвертом квадрантах. Эти площади, в свою очередь, разобьем на
элементарные площадки. Видно, что для элементарных площадок, расположенных в
первом и третьем квадрантах, расстояния от элементарных площадок до координатных
осей имеют одинаковый знак. Поэтому при интегрировании по площади, расположенной в этих квадрантах мы получим знак «плюс». В четвертом квадранте расстояния от
площадок до координатных осей имеют разные знаки, что при интегрировании даст
знак «минус». Очевидно, что, суммируя полученные результаты, мы, в итоге, получим
положительное значение центробежного момента инерции уголка. Следовательно,
1
I x1 y1   76,35  19,97   28,19 см4.
2
Теперь определяем координаты центров тяжести отдельных элементов Ci в центральных осях x0 и y0 :
для уголка
x01  x1  xc  2,02  4,93  6,95 см;
y01  y1  yc  17,02  5,99  11,03 см;
для швеллера
x02  x2  xc  2,21  4,93  2,72 см;
y02  y2  yc  11,00  5,99  5,01 см;
для полосы
x03  x3  xc  9,00  4,93  4,07 см;
3. Темы, варианты и примеры решения задач
30
y03  y3  yc  1,00  5,99  6,99 см.
Дальнейшие вычисления производим в табличной форме (табл. 3.7).
Таблица 3.7
Определение моментов инерции сечения относительно центральных осей x0 и y0
Моменты инерции относительно
Координаты центра тяжеПлощадь
4
Номер Наименова- элемента собственных центральных осей xi и yi , см сти в осях x 0 и y0 , см
элемента ние элемента
Fi , см2
I
I
I
x
y
1
2
3

Уголок
Швеллер
Полоса
Все сечение
10,67
26,70
36,00
73,37
xi
yi
xi yi
48,16
2110,00
12,00
48,16
151,00
972,00
28,19
0
0
0i
0i
-6,95
-2,72
4,07
11,03
5,01
-6,99
Продолжение табл. 3.7
Наименование
элемента
Уголок
Швеллер
Полоса
Все сечение
Моменты инерции относительно
центральных осей xс и y с , см4
«Переносные» моменты
инерции, см4
x02i Fi
515,39
197,54
596,34
y02i Fi
I xi  y02i Fi
x0i y0i Fi
1298,12
670,17
1758,96
-817,95
-363,85
-1024,17
I y i  x02i Fi
1346,28
2780,17
1770,96
5897,41
563,55
348,54
1568,34
2480,43
I xi yi  x0i y0i Fi
-789,76
-363,85
-1024,17
-2177,78
После округления вычисленных значений моментов инерции до трех значащих
цифр, окончательно, получим
I x0  5900 см4;
I y 0  2480 см4;
I x0 y0  2180 см4.
3. Определяем положение главных центральных осей инерции u и v.
Угол наклона главных центральных осей u и v к осям x0 и y0 , соответственно,
определяем из следующей формулы:
2I x y
 2  2180
;
tg 2 0  
tg 2 0  
 1,27 .
Ix  Iy
5900  2480
0
0
0
0
Отсюда находим, что 2 0  51,8 и  0  25,9 .
Откладываем положительное значение угла  0 от оси x0 против хода часовой
стрелки и проводим главные центральные оси u и v (см. рис. 3.11).
Поскольку I x0  5900 см4 больше I y 0  2480 см4, ось u является осью, относительно которой момент инерции сечения максимален, то есть ось u – ось max. Соответственно, ось v является осью min.
4. Вычисляем значения главных центральных моментов инерции I max и I min для
заданного поперечного сечения.
Ix  Iy
1
2
I max, min 

I x  I y  4 I x2 y ;
2
2
5900  2480 1
5900  24802  4   21802  4190  2770 см4;
I max, min 

2
2
I max  I u  4190  2770  6960 см4;
0
0

0
0

0
0
3. Темы, варианты и примеры решения задач
31
I min  I v  4190  2770  1420 см4.
Контролем правильности последних вычислений может служить следующая проверка:
I x0  I y0  I max  I min .
5900  2480  6960  1420 ;
7380  7380 .
3.6. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ
Задача 6
Для двух заданных схем балок (рис. 3.11) требуется:
 построить эпюры перерезывающих сил ( Q y ) и изгибающих моментов ( M z );
 подобрать из условия прочности по нормальным напряжениям
(    16 кН/см2) балку круглого поперечного сечения (рис. 3.11, a) и балку
двутаврового поперечного сечения (рис. 3.11, б);
 проверить прочность подобранных балок по касательным напряжениям
(    8 кН/см2).
Данные взять из табл. 3.8.
Таблица 3.8
Исходные данные к задаче 6
Начальная буква фамилии, Номер схемы
имени, отчества
(рис. 3.11)
1
2
А, П
1
Б, Р
2
В, С
3
Г, Т
4
Д, У
5
Е, Ф
6
Ж, Х
7
З, Ц
8
И, Ч
9
К, Ш
0
Л, Щ
1
М, Э
2
Н, Ю
3
О, Я
4
l,
м
3
3
4
5
6
3
4
5
6
3
4
5
6
3
4
a1 l
a2 l
a3 l
4
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,2
0,3
0,4
0,5
0,6
0,7
0,8
5
0,6
0,5
0,4
0,3
0,7
0,5
0,4
0,6
0,5
0,4
0,3
0,7
0,3
0,6
6
0,2
0,3
0,3
0,2
0,2
0,3
0,6
0,3
0,4
0,2
0,4
0,5
0,4
0,3
M,
кН·м
7
8
7
6
5
4
8
7
6
5
4
5
4
3
2
P,
кН
8
5
6
7
8
9
10
5
6
7
8
2
3
4
5
q,
кН/м
9
10
11
12
13
14
9
10
11
12
8
9
10
11
12
Пример 6.1
Для консольной балки, нагруженной распределенной нагрузкой q  20 кН/м и сосредоточенным моментом M  50 кН·м (рис. 3.12), требуется: построить эпюры перерезывающих сил Q y и изгибающих моментов M z , подобрать балку круглого поперечного сечения при допускаемом нормальном напряжении    16 кН/см2 и проверить
прочность балки по касательным напряжениям при допускаемом касательном напряжении    8 кН/см2. Размеры балки a1  1 м; a2  2 м; l  4 м.
Решение
1. Определяем опорные реакции.
Горизонтальная реакция в заделке H A равна нулю, поскольку внешние нагрузки в
направлении оси z на балку не действуют.
3. Темы, варианты и примеры решения задач
32
а)
q
M
1
P
q
а)
2
P
б)
M
б)
q
q
q
q
P
3
q
P
M
M
P
P
а)
P
M
P
а)
б)
б)
q
M
4
P
а)
б)
q
5
a1
M
а)
6
a1
a2
l
б)
P
q
M
P
M
P
a2
l
q
a3
q
M
P
а)
б)
q
P
7
q
q
M
M
а)
P
б)
q
q
M
8
P
a1
a3
P
а)
б)
q
9
a2
l
P
q
M
а)
P
q
б)
0
a1
P
l
a1
a2
Рис. 3.11
q
M
l
a2
3. Темы, варианты и примеры решения задач
33
Выбираем направления остальных реактивных усилий, возникающих в заделке:
вертикальную реакцию R A направим вниз, а момент M A – по ходу часовой стрелки.
Их значения определяем из уравнений статики:
 M A  0;  Y  0 .
Составляя эти уравнения, считаем момент положительным при вращении против
хода часовой стрелки, а проекцию силы положительной, если ее направление совпадает
с положительным направлением оси y.
Из первого уравнения находим момент в заделке ( M A ):
 a 
 M A   M A  M  qa2  l  22   0;


 a 
M A   M  qa2  l  2  ;
2

2

M A  50  20  2   4    70 кН·м.
2

Из второго уравнения – вертикальную реакцию ( R A ):
RA  qa2 ;
Y  RA  qa2  0;
RA  20  2  40 кН.
Полученные нами положительные значения M A и R A свидетельствуют о том, что
мы угадали их направления.
а)
М = 50 кН∙м
МА = 70 кН∙м
1
2 3
q = 20 кН/м
4 5
6
А
RА = 40 кН
a2 = 2 м
a1 = 1 м
l=4м
Q
б)
40
в)
кН
40
40
40
40
40
МИ кН∙м
Рис. 3.12
2. Строим эпюры перерезывающих сил ( Q y ) и изгибающих моментов ( M x ).
В соответствии с характером закрепления и нагружения балки разбиваем ее длину
на три участка. По границам каждого их этих участков наметим шесть поперечных сечений (см. рис. 3.12), в которых мы и будем методом сечений (РОЗУ) вычислять значения перерезывающих сил и изгибающих моментов.
Сечение 1. Отбросим мысленно правую часть балки. Заменим ее действие на
оставшуюся левую часть перерезывающей силой Q y1 и изгибающим моментом M x1 .
3. Темы, варианты и примеры решения задач
34
Для удобства вычисления их значений закроем отброшенную нами правую часть балки
листком бумаги, совмещая левый край листка с рассматриваемым сечением.
Напомним, что перерезывающая сила, возникающая в поперечном сечении,
должна уравновесить все внешние силы (активные и реактивные), которые действуют
на рассматриваемую (видимую) нами часть балки. Поэтому перерезывающая сила
должна быть равна алгебраической сумме всех сил, которые мы видим.
В данном случае мы видим только реакцию опоры R A , направленную вниз. Таким образом:
Q y1   R A  40 кН.
Знак «минус» нами взят, потому что сила R A вращает видимую нами часть балки
относительно первого сечения (края листка) против хода часовой стрелки.
Изгибающий момент в сечении должен уравновесить момент, создаваемый видимыми нами внешними усилиями, относительно рассматриваемого сечения. Поэтому он
равен алгебраической сумме моментов всех усилий, которые действуют на рассматриваемую нами часть балки, относительно рассматриваемого сечения.
Мы видим два усилия: реакцию R A и момент в заделке M A . Однако у силы R A
плечо равно нулю, поэтому
M x1   M  70 кН·м.
Здесь знак «плюс» нами взят, потому что реактивный момент M A изгибает видимую нами часть балки выпуклостью вниз.
Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка нами мысленно представляется жесткой заделкой).
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки.
Теперь в отличие от первого сечения у силы R A появилось плечо: a1  1 м. Поэтому
Q y 2   R A  40 кН;
M x 2   M A  RAа1 ;
M x 2  70  40  1  30 кН·м.
Сечение 3. Закрывая правую часть балки, найдем
Q y 3   R A  40 Кн;
M x 3   M A  RAa1  M ;
M x 3  70  40  1  50  80 кН·м.
Сечение 4. Закроем листком левую часть балки. Тогда
Q y 4   qa2 ;
Q y 4  20  2  40 кН;
a2
2
M x 4  20  2   40 кН·м.
;
2
2
Сечение 5. По-прежнему, закроем левую часть балки. Будем иметь:
Q y 5   qa2 ;
Q y 5  20  2  40 кН;
M x 4   qa2
a2
2
M x 5  20  2   40 кН·м.
;
2
2
Сечение 6. Опять закроем левую часть балки. Получим:
Qy6  M x6  0 .
M x 5   qa2
По найденным значениям строим эпюры перерезывающих сил Q y (рис. 3.12, б) и
изгибающих моментов M x (рис. 3.12, в).
3. Темы, варианты и примеры решения задач
35
Под незагруженными участками эпюра перерезывающих сил идет параллельно
оси балки, а под распределенной нагрузкой q – по наклонной прямой вверх. На эпюре
Q y имеется скачок вниз на 40 кН под реакцией R A .
На эпюре изгибающих моментов мы видим излом под опорной реакцией R A .
Угол излома направлен навстречу реакции опоры. Под распределенной нагрузкой q
эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре M x – экстремум, поскольку эпюра перерезывающей
силы в этом месте проходит здесь через нулевое значение.
3. Определяем требуемый диаметр поперечного сечения балки.
Условие прочности по нормальным напряжениям имеет вид:
M x max
 max 
  ,
Wx
где W x – момент сопротивления балки при изгибе. Для балки круглого поперечного сечения он равен:
d 3
Wx 
 0,1d 3 .
32
Наибольший по абсолютному значению изгибающий момент возникает в третьем
сечении балки:
M x max  M x3  8000 кН·см.
Тогда требуемый диаметр балки определяется по формуле:
d треб  3
d треб  3
M x3
0,1 
;
8000
 17,1 см.
0,1  16
Принимаем d  170 мм. Тогда
 max 
Mx
max
Wx
;
8000
 16,6 кН/см2;
  17 3
32
16,6 кН/см2     16 кН/см2.
«Перенапряжение» составляет:
16,6  16
 100  3,75 %;
16
3,75 %  5 % ,
что допускается.
4. Проверяем прочность балки по наибольшим касательным напряжениям.
Наибольшие касательные напряжения, возникающие в поперечном сечении балки
круглого сечения, вычисляются по формуле:
4 Qy
max
,
 max 
3F
где F  d 2 4 – площадь поперечного сечения балки.
 max 
3. Темы, варианты и примеры решения задач
36
Согласно эпюре Q y наибольшее по алгебраической величине значение перерезывающей силы равно Q y
max
 40 кН. Тогда
 max 
4 Qy
max
3F
;
4  40
 0,235 кН/см2,
2
  17
3
4
0,235 кН/см2     8 кН/см2.
То есть условие прочности и по касательным напряжениям выполняется.
 max 
Пример 6.2
Для шарнирно опертой балки, нагруженной распределенной нагрузкой q  20
кН/м, сосредоточенной силой P  50 кН и сосредоточенным моментом M  60 кН·м
(рис. 3.13), требуется построить эпюры перерезывающих сил ( Q y ) и изгибающих моментов ( M z ) и подобрать балку двутаврового поперечного сечения при допускаемом
нормальном напряжении    16 кН/см2 и допускаемом касательном напряжении
   8 кН/см2. Пролет балки l  6 м.
RA = 37,5 кН
а)
М = 60 кН∙м
RВ = 132,5 кН
B
4 5
A
1
2 3
Р = 50 кН
6
q = 20 кН/м
0,5l = 3 м
l=6м
a=6м
50
37,5
50
б)
Qy кН
1,875 м
22,5
82,5
35,16
22,5
82,5
в)
Мx кН∙м
75
Рис. 3.13
Решение
1. Определяем опорные реакции.
Для заданной балки необходимо найти три опорные реакции: R A , H A и R B . Поскольку на балку действуют только вертикальные нагрузки, перпендикулярные к ее
оси, горизонтальная реакция неподвижной шарнирной опоры равна нулю:
3. Темы, варианты и примеры решения задач
37
HA  0 .
Направления вертикальных реакций R A и R B выбираем произвольно. Направим,
например, обе вертикальные реакции вверх. Для вычисления их значений составим два
уравнения статики:
M A  0;
 M B  0.
Предварительно найдем равнодействующую распределенной погонной нагрузки
q . Очевидно, что она равна площади эпюры этой нагрузки q  l и приложена в центре
тяжести этой эпюры, то есть посередине участка длиной l . Тогда
l
 l
 M A   RB l  ql 2  P l  4   M  0;


6
6
l

 l
20  6   50   6    60
q l   P l    M
2
4
2

 4
RB 
 132,5 кН;
;
RB 
6
l
l
l
 M B   R Al  M  P 4  ql 2  0 ;
6
6
l
l
 60  50   20  6 
 M  P  ql
4
2  37,5 кН.
4
2;
RA 
RA 
l
6
Делаем проверку:  Y  0 . Силы, направление которых совпадает с положительным направлением оси y, проектируются (проецируются) на эту ось со знаком «плюс»:
Y  RA  P  RB  ql  0;
37,5  50  132,5  2  60  0;
0  0,
то есть верно.
2. Строим эпюры перерезывающих сил Q y и изгибающих моментов M z .
Разбиваем длину балки на отдельные участки. Границами этих участков являются
точки приложения сосредоточенных усилий (активных и/или реактивных), а также точки, соответствующие началу и окончанию действия распределенной нагрузки. Таких
участков получается три. По границам этих участков наметим шесть поперечных сечений, в которых мы и будем вычислять значения перерезывающих сил и изгибающих
моментов (рис. 3.13, а).
Сечение 1. Отбросим мысленно правую часть балки. Для удобства вычисления
перерезывающей силы Q y1 и изгибающего момента M x1 , возникающих в этом сечении,
закроем отброшенную нами часть балки листком бумаги, совмещая левый край листка
с самим сечением.
Перерезывающая сила в сечении балки равна алгебраической сумме всех внешних
сил (активных и реактивных) которые мы видим. В данном случае мы видим реакцию
опоры R A и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
Q y1   R A  37,5 кН.
Знак «плюс» взят, потому что сила R A вращает видимую нами часть балки относительно первого сечения (края листка) по ходу часовой стрелки.
Изгибающий момент в сечении балки равен алгебраической сумме моментов всех
усилий, которые мы видим, относительно рассматриваемого сечения (то есть относи-
3. Темы, варианты и примеры решения задач
38
тельно края листка). Мы видим только реакцию опоры R A . Однако у силы R A плечо
равно нулю. Поэтому
M x1  0 .
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Мы видим реакцию R A и распределенную нагрузку q, действующую на участке
длиной l 2 . Равнодействующая погонной нагрузки равна ql 2 . Она приложена посередине участка длиной l 2 . Поэтому
l
6
Qy 2   RA  q ;
Q y 2  37,5  20   22,5 кН;
2
2
l
l l
6
6 6
M x 2   RA  q
M x 2  37,5   20    22,5 кН·м.
;
2
24
2
2 4
Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении. То есть левый край листка нами мысленно представляется жесткой заделкой.
Сечение 3. Закроем правую часть. Получим:
l
6
Qy 3   RA  q ;
Q y 3  37,5  20   22,5 кН;
2
2
l
l l
6
6 6
M x 3   RA  q
M ;
M x 3  37,5   20    60  82,5 кН·м.
2
24
2
2 4
Сечение 4. Закрываем листком правую часть балки. Тогда
Q y 4  37,5  2  60  82,5 кН;
Q y 4   RA  ql ;
l
6
M ;
M x 4  37,5  6  20  6   60  75 кН·м.
2
2
Теперь для контроля правильности вычислений закроем листком бумаги левую
часть балки. Мы видим сосредоточенную силу P, реакцию правой опоры RB и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
Q y 4  50  132,5  82,5 кН;
Q y 4   P  RB ;
M x 4   RAl  ql
M x4  P
l
;
4
M x 4  50 
6
 75 кН·м.
4
То есть все верно.
Сечение 5. По-прежнему закроем левую часть балки. Будем иметь:
Q y 5   P  5 кН;
l
6
M x5   P ;
M x 5  5   7,5 кН·м.
4
4
Сечение 6. Опять закроем левую часть балки. Получим:
Q y 6   P  50 кН;
M x6  0 .
По найденным значениям строим эпюры перерезывающих сил Q y (рис. 3.13, б) и
изгибающих моментов M x (рис. 3.13, в).
Убеждаемся в том, что под незагруженным участком эпюра перерезывающих сил
идет параллельно оси балки, а под распределенной нагрузкой q – по прямой, имеющей
3. Темы, варианты и примеры решения задач
39
наклон вниз. На эпюре Q y имеется три скачка: под реакцией R A – вверх на 37,5 кН,
под реакцией RB – вверх на 132,5 кН и под силой P – вниз на 50 кН.
На эпюре изгибающих моментов мы видим изломы под сосредоточенной силой P
и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. Под сосредоточенным моментом – скачок на
60 кН ·м, то есть на величину самого момента. В сечении 7 на эпюре M x – экстремум,
поскольку эпюра перерезывающей силы в этом месте проходит через нулевое значение
( Q y 7  0 ). Определим расстояние z от этого сечения до левой опоры.
Перерезывающая сила равна:
Qy 7   RA  qz ;
Q y 7  37,5  20 z  0 ,
отсюда
37,5
R
z
 1,875 м.
z A ;
20
q
Экстремальное значение изгибающего момента в сечении 7 равно:
z
M x 7   RA z  qz ;
2
1,875
M x 7  37,5  1,875  20  1,875 
 35,2 кН·м.
2
3. Определяем требуемый момент сопротивления балки из условия прочности
по нормальным напряжениям.
Согласно эпюре M x , максимальный изгибающий момент возникает в третьем поперечном сечении балки:
M x max  M x3  8250 кН·см.
Тогда
Mx
8250
 516 см3.
16
 
По сортаменту (ГОСТ 8239 – 72) подбираем двутавр № 30а, имеющий Wx  518 см3.
4. Проверяем прочность балки по наибольшим касательным напряжениям.
Наибольшие касательные напряжения, возникающие в поперечном сечении двутавровой балки, вычисляются по формуле:
Qy
S
max x
.
 max 
I xd
По сортаменту для выбранного нами двутавра определяем:
статический момент половины сечения относительно нейтральной оси:
S x  292 см3;
момент инерции относительно нейтральной оси:
I z  7780 см4;
толщина стенки:
d  0,65 см.
Согласно эпюре Q y наибольшее по алгебраической величине значение перерезы-
Wxтреб 
max
W xтреб 
;
вающей силы:
Qy
max
 82,5 кН.
3. Темы, варианты и примеры решения задач
40
Тогда
82,5  292
 4,76 кН/см2;
I xd
7780  0,65
4,76 кН/см2     8 кН/см2,
то есть условие прочности по касательным напряжениям выполняется.
 max 
Qy
max
Sx
 max 
;
3.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКИ
Задача 7
Раскрыть статическую неопределимость балки (рис. 3.14) с использованием универсального уравнения упругой линии балки. Построить эпюры перерезывающих сил
Q y и изгибающих моментов M z .
Данные взять из табл. 3.9.
M = βql2
q
P = αql
1
q
5
P = αql
q
P = αql
P = αql
2
q
6
q
P = αql
P = αql
3
q
P = αql
7
q
P = αql
M = βql2
4
P = αql
P = αql
q
8
0,5l
0,5l
αl
l
P = αql
αl
l
Рис. 3.14
Таблица 3.9
Исходные данные к задаче
Начальная буква фами- Номер схемы
лии, имени, отчества
(рис. 3.14)
1
А, П
Б, Р
В, С
Г, Т
Д, У
Е, Ф
Ж, Х
2
1
2
3
4
5
6
7


3
0,9
1,0
0,9
0,8
0,7
0,6
0,5
4
0,1
0,2
0,3
0,4
0,5
0,9
–
Начальная буква фами- Номер схемы
лии, имени, отчества
(рис. 3.14)
1
З, Ц
И, Ч
К, Ш
Л, Щ
М, Э
Н, Ю
О, Я
2
8
1
2
3
4
5
6


3
0,4
0,5
0,7
0,6
0,5
0,4
0,3
4
–
0,6
0,8
0,7
0,6
0,5
0,4
3. Темы, варианты и примеры решения задач
41
Пример 7
Требуется раскрыть статическую неопределимость балки, нагруженной равномерно распределенной нагрузкой q и сосредоточенным моментом M  0,1ql 2
(рис. 3.15), и построить эпюры перерезывающих сил Q y и изгибающих моментов M z .
а)
RA = 0,775ql
q
B
А
МA = 0,175ql 2
б)
l
0,775ql
Qy
0,225ql
0,775l
0,151ql 2
в)
0,1ql 2
Mx
0,175ql 2
Рис. 3.15
Решение
1. Определяем степень статической неопределимости.
Заданная балка один раз статически неопределима, поскольку для нахождения четырех реактивных усилий RA , H A , M A и RB мы имеем только три уравнения статики:
 X  0; Y  0;  M  0 .
2. Составляем уравнения равновесия.
Из первого уравнения статики  X  0 мы легко находим, что горизонтальная
реакция жесткой заделки H A  0 .
Второе уравнение дает:
Y  ql  RA  RB  0
или
RA  RB  ql .
Сумма моментов всех внешних и реактивных усилий относительно точки A приводит к следующему уравнению:
l
 M A  RB l  M  ql 2  M A  0 .
Отсюда
M A  RB l  0,5ql 2  0,1ql 2  0,4ql 2 .
3. Для раскрытия статической неопределимости нам необходимо записать одно
дополнительное условие, касающееся деформации балки.
3. Темы, варианты и примеры решения задач
42
Таким условием, например, может являться условие отсутствия прогиба балки на
опоре B при z  l : v(l )  0 .
Воспользуемся универсальным уравнением упругой линии балки. Прогиб балки в
произвольном сечении с координатой z, согласно этому уравнению, определяются по
следующей формуле:
2
3
4
4
M z  a 
P z  b 
qz  b 
qz  b 
v( z )  v(0)   (0) z 



,
2 EI x
6 EI x
24 EI x
24 EI x
где v (0) и  (0) – прогиб и угол поворота поперечного сечения балки в начале координат; a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P; c и d – координаты начала и конца участка, нагруженного распределенной
нагрузкой.
В случае многократного повторения однотипных нагрузок необходимо использовать суммирование соответствующих слагаемых.
Заметим, что в приведенную выше формулу входят только те внешние усилия
(активные и реактивные), которые расположены левее сечения, в котором определяется
прогиб балки.
Поскольку в заделке v(0)   (0)  0 , условие отсутствия прогиба в точке B примет вид:
v(l )  
2
M A l  0
R l  0 ql  04 ql  l 4
M l  l 

 A


0
2 EI x
2 EI x
6 EI x
24 EI x
24 EI x
2
3
или
 12M A  4 R Al  ql 2  0 .
Таким образом, мы имеем систему из трех уравнений с тремя неизвестными:
RA  RB  ql ;
M A  RB l  0,4ql 2 ;
 12M A  4 R Al  ql 2 .
Решая ее, находим, что
R A  0,775ql ; RB  0,225ql ; M A  0,175ql 2 .
4. Строим эпюры перерезывающих сил Q y и изгибающих моментов M z .
Сечение 1. Отбросим мысленно правую часть балки. Мы видим реакцию опоры
R A и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
Q y1   R A  0,775ql .
Знак «плюс» нами взят, потому что сила R A вращает видимую нами часть балки
относительно первого сечения по ходу часовой стрелки.
Изгибающий момент в сечении балки равен алгебраической сумме моментов всех
усилий, которые мы видим, относительно рассматриваемого сечения. Мы видим реакцию опоры R A , у которой плечо равно нулю, и момент в заделке M A  0,175ql 2 . Поэтому
M x1   M A  0,175ql 2 .
Сечение 2. Закроем левую часть балки. Получим:
Q y 2   RB  0,225ql ;
M x 2  M  0,1ql 2 .
3. Темы, варианты и примеры решения задач
43
По найденным значениям строим эпюры перерезывающих сил Q y (рис. 3.15, б) и
изгибающих моментов M x (рис. 3.15, в).
В сечении 3 на эпюре M x – экстремум, поскольку эпюра перерезывающей силы в
этом месте проходит здесь через нулевое значение ( Q y 3  0 ). Определим расстояние z
от этого сечения до левой опоры.
Перерезывающая сила равна:
Q y 3   R A  qz  0,775ql  qz  0 ,
отсюда
R
0,775ql
z A 
 0,775l .
q
q
Тогда экстремальное значение изгибающего момента в сечении 3 равно:
z
0,775l
M x 3   R A z  M A  qz  0,775ql  0,775l  0,175ql 2  q  0,775l 
 0,125ql 2 .
2
2
3.8. ВНЕЦЕНТРЕННОЕ СЖАТИЕ
Задача 8
Короткий чугунный стержень с поперечным сечением, изображенным на
рис. 3.16, сжимается продольной силой P, приложенной в точке A. Определить
наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении стержня, выразив их через силу P и размеры сечения. Найти допускаемую нагрузку
( Pдоп ) при заданных допускаемых напряжениях для материала на сжатие
 с   12 кН/см2 и на растяжение  р  2,5 кН/см2. Данные взять из табл. 3.10.
 
2
b
3a
a
1
1
3b
4a
2a
А(Р)
4b
2b
А(Р)
3a
a
3
4
А(Р)
Рис. 3.16
b
3b
4a
2a
А(Р)
4b
2b
3. Темы, варианты и примеры решения задач
44
5
b
3b
a
3a
А(Р)
6
А(Р)
2b
4b
А(Р)
8
А(Р)
4a
4b
3b
7
2b
2a
3a
2a
4a
0
4b
2a
9
2b
4a
А(Р)
А(Р)
a
b
Рис. 3.16 (продолжение)
Таблица 3.10
Исходные данные к задаче 8
Начальная буква фами- Номер схемы
лии, имени, отчества
(рис. 3.16)
1
2
А, П
1
Б, Р
2
В, С
3
Г, Т
4
Д, У
5
Е, Ф
6
Ж, Х
7
a,
cм
3
30
40
50
60
70
80
90
b,
см
4
50
80
70
30
40
50
60
Начальная буква фами- Номер схемы
лии, имени, отчества
(рис. 3.16)
1
2
З, Ц
8
И, Ч
9
К, Ш
10
Л, Щ
1
М, Э
2
Н, Ю
3
О, Я
4
a,
cм
3
100
30
40
50
60
80
100
b,
см
4
70
40
30
60
70
40
50
Пример 8
Короткий чугунный стержень (рис. 3.17, а) с поперечным сечением, изображенным на рис. 3.17, б, сжимается продольной силой P, приложенной в точке A. Определить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном
сечении стержня, выразив их через силу P и размеры сечения a  5 см, b  8 см. Найти
допускаемую нагрузку P  при заданных допускаемых напряжениях для материала на
сжатие  с   12 кН/см2 и на растяжение  р  2,5 кН/см2.
 
3. Темы, варианты и примеры решения задач
45
Решение
Действующая на стержень сила P, помимо сжатия, осуществляет изгиб стержня относительно главных центральных осей x и y. Изгибающие моменты, соответственно, равны:
M x  Py p ; M y  Px p ,
где x p   a  5 см и y p  b  8 см – координаты точки приложения силы P (координаты точки A).
а)
xР = a
б)
1
Р
2
N
А(Р) 3
yP = b
8
2b
X
aY = -b
4b
aX = -a
a = 5 см
b = 8 см
7•
4
5
6
2a
N
4a
Рис. 3.17
Нормальные напряжения в некоторой точке с координатами x и y любого поперечного сечения стержня определяются по формуле:
P  xpx yp y 
   1  2  2  ,
F 
iy
i x 
где F – площадь, а i x и i y – радиусы инерции поперечного сечения.
1. Определяем геометрические характеристики поперечного сечения стержня.
Площадь сечения стержня равна
F  4a  2b  2  2a  b  12ab .
Главные центральные моменты инерции определяем следующим образом:
2a  4b 3
a  2b 3
Ix 
2
 12ab 3 ;
12
12
3
2b  4a 
b  2a 3
Iy 
2
 12a 3b .
12
12
Квадраты радиусов инерции равны:
3. Темы, варианты и примеры решения задач
46
I x 12ab 3


 b2 ;
F
12ab
I y 12a 3b
i y2 

 a2 .
F
12ab
2. Определяем положение нулевой линии.
Отрезки a x и a y , отсекаемые нулевой линией от осей координат, равны:
i x2
i y2
a2
ax  

 a  5 см;
xp
a
i x2
b2
   b  8 см.
yp
b
Показываем нулевую линию N – N (см. рис. 3.18, б). Нулевая линия делит поперечное сечение на две области, одна из которых испытывает растяжение, а другая –
сжатие. На рисунке растянутая область нами заштрихована.
3. Вычисляем наибольшее растягивающее напряжение.
Оно возникает в точках 6 и 7, наиболее удаленных от нулевой линии. Значение
этого напряжения, вычисленное, например, для точки 6 равно:
y y 
P x x
P  a   a  b   2b  
P
 6   1  p2 6  p2 6   
1


;
2
2


F
iy
ix 
12ab 
a
b
 6ab
P
P
6 

.
6  5  8 240
4. Вычисляем наибольшее сжимающее напряжение.
Оно возникает в точках 2 и 3, наиболее удаленных от нулевой линии. Значение
этого напряжения, вычисленное, например, для точки 2 равно:
y y 
P x x
P  a  a b  2b 
P
 2   1  p2 2  p2 2   
1 2  2   
;

F
iy
ix 
12ab 
a
b 
3ab
P
P
2  

.
358
120
5. Определяем допускаемую нагрузку из условия прочности на растяжение:
P
  р  2,5 кН/см2;
240
P  2,5  240  600 кН.
6. Определяем допускаемую нагрузку из условия прочности на сжатие:
P
  c   12 кН/см2;
120
P  12 120  1440 кН.
7. Допускаемая нагрузка равна меньшему из двух найденных значений:
P  600 кН.
ay  
 
3.9. ИЗГИБ С КРУЧЕНИЕМ
Задача 9
На рис. 3.18 в аксонометрии изображен стальной ломаный стержень круглого поперечного сечения, расположенный в горизонтальной плоскости и имеющий прямые
углы в точках A и B. На стержень действует вертикальная нагрузка. Требуется построить отдельно в аксонометрии эпюры изгибающих и крутящих моментов, установить
3. Темы, варианты и примеры решения задач
47
С
αl
l
1
С
В
А
l
αl
2
А
αl
q
q
αl
l
P = ql
P = ql
αl
l
С
l
q
3
l
4
В
l
αl
В
αl
P = ql
А
αl
P = ql
С
αl
С
αl
l
q
В
6
В
l
αl
l
l
А
P = ql
αl
С
αl
q
7
А
В
l
С
P = ql
αl
8
αl
А
q
αl
l
В
l
αl
С
P = ql
P = ql
q
А
С
q
l
q
9
С
q
А
5
l
В
А
А
В
αl
P = ql
0
В
αl
l
αl
P = ql
Рис. 3.18
αl
3. Темы, варианты и примеры решения задач
48
опасное сечение, найти для него расчетный момент по третьей теории прочности и подобрать диаметр стержня. Допускаемое нормальное напряжение    16 кН/см2;
l  1 м; q  2 кН/м. Остальные данные взять из табл. 3.11.
Таблица 3.11
Исходные данные к задаче 9
Начальная буква фамилии, Номер схемы
имени, отчества
(рис. 3.18)
1
2
А, П
1
Б, Р
2
В, С
3
Г, Т
4
Д, У
5
Е, Ф
6
Ж, Х
7

3
1,5
1,4
1,3
1,2
1,1
1,0
0,9
Начальная буква фамилии, Номер схемы
имени, отчества
(рис. 3.18)
1
2
З, Ц
8
И, Ч
9
К, Ш
0
Л, Щ
1
М, Э
2
Н, Ю
3
О, Я
4

3
0,8
0,7
0,6
0,7
0,8
0,9
1,0
Пример 9
На стальной ломаный стержень круглого поперечного сечения, расположенный в горизонтальной плоскости и имеющий прямые углы в точках B и C (рис. 3.19, а), действует
вертикальная нагрузка. Требуется построить отдельно в аксонометрии эпюры изгибающих и
крутящих моментов, установить опасное сечение, найти для него эквивалентный момент по
третьей гипотезе прочности и подобрать диаметр стержня. Допускаемое нормальное
напряжение    16 кН/см2; a  1 м; b  1 м; c  0,5 м; q  3 кН/м; P  2 кН.
q = 3 кН/м
Р = 2 кН
а)
А
В
1
2 3
a = 1м
С
D
4 5c = 0,5м6
b =1м
ммм
мм
МX кН∙м
3,5
б)
4,5
2,0
2,0
3,5
3,5
МZ кН∙м
2,0
в)
2,0
Рис.3.19
3. Темы, варианты и примеры решения задач
49
Решение
1. Строим эпюры изгибающих и крутящих моментов.
Разбиваем длину стержня на три участка: AB, BC и CD. Делаем сечения по границам каждого из этих участков и вычисляем значения изгибающего ( M изг ) и крутящего
( M кр ):
M 1изг  0 , M 1кр  0 ;
M 2изг  Pa  2 1  2 кН·м (сжаты волокна снизу);
M 2кр  0 ;
M 3изг  0 ;
M 3кр  Pa  2 1  2 кН·м;
b
1
M 4изг  qb  Pa  3 1   2 1  3,5 кН·м (сжаты волокна снизу);
2
2
кр
M 4  Pa  2 1  2 кН·м;
M 5изг  Pa  2 1  2 кН·м (сжаты волокна снизу);
b
1
M 5кр   Pb  qb  2 1  3 1   3,5 кН·м;
2
2
изг
M 6  Pa  c  qbc  2  1  0,5  3 1 0,5  4,5 кН·м (сжаты волокна снизу);
b
1
M 6кр   Pb  qb  2 1  3 1   3,5 кН·м;
2
2
По найденным значениям строим эпюры изгибающих ( M изг ) и крутящих ( M кр )
моментов.
При построении эпюры изгибающих моментов ( M изг ) придерживаемся следующих правил:
 плоскость эпюры на каждом из участков ломаного стержня совпадает с плоскостью изгиба соответствующего участка;
 ординаты эпюры откладываются со стороны сжатых волокон.
Эпюра изгибающих моментов ( M изг ) показана на рис. 3.19, б. Под незагруженными участками AB и CD она линейна, а под распределенной нагрузкой изменяется по
квадратичной параболе.
Для крутящего момента сохраняем обычное правило знаков. Эпюра крутящих
моментов ( M кр ) может быть ориентирована в пространстве как угодно, но ее ординаты
всегда откладываются по нормали к оси стержня (рис. 3.19, в).
2. Устанавливаем опасное сечение.
Несложный анализ построенных эпюр показывает, что опасным является сечение
6, в котором возникают и наибольший изгибающий, и наибольший крутящий моменты:
M 6изг  4,5 кН·м;
M 6кр  3,5 кН·м.
3. Вычисляем эквивалентный момент по третьей гипотезе прочности:
( 3)
M экв

M   M 
изг 2
6
кр 2
6
;
( 3)
M экв
 4,5 2  3,5 2  5,70 кН·м  570 кН·см.
4. Подбираем диаметр стержня.
Из условия прочности требуемый осевой момент сопротивления равен:
3 
 d 3 M экв
треб
;
W


 
32
3. Темы, варианты и примеры решения задач
50
W треб 
570
 35,6 см3.
16
Отсюда
d 3
Принимаем d  72 мм.
35,6  32

 7,13 см.
3.10. УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
Задача 10
Вертикальный стальной стержень (марка стали Ст.3), поперечное сечение которого
показано на рис. 3.20, сжимается с торца силой P. Определить значение критической и допускаемой нагрузок. Допускаемое напряжение    16 кН/см2, модуль Юнга E  2104
кН/см2. Решение задачи получить для двух вариантов закрепления концов стержня: оба конца шарнирно оперты; оба конца жестко защемлены. Данные взять из табл. 3.12.
3
4
1,5a
2a
a
2a
1,2a
6
a
a
2a
7
8
9
0
a
2a
1,5a
2a
a
2a
1,5a
2a
1,5a
2a
a
2a
5
1,5a
2
1,5a
1
1,2a
2a
Рис. 3.20
Таблица 3.12
Исходные данные к задаче 10
Начальная буква фами- Номер схемы
лии, имени, отчества
(рис. 3.20)
1
2
А, П
1
Б, Р
2
В, С
3
Г, Т
4
Д, У
5
Е, Ф
6
Ж, Х
7
l,
м
3
2,4
2,8
3,0
3,5
4,0
4,5
5,0
a,
см
4
6
7
8
9
10
6
7
Начальная буква фами- Номер схемы
лии, имени, отчества
(рис. 3.20)
1
2
З, Ц
8
И, Ч
9
К, Ш
0
Л, Щ
1
М, Э
2
Н, Ю
3
О, Я
4
l,
м
3
2,5
2,7
2,9
3,2
3,8
4,4
4,9
a,
см
4
8
9
10
6
7
8
9
3. Темы, варианты и примеры решения задач
51
Пример 10
Вертикальный стальной стержень (марка стали Ст. 3), поперечное сечение которого показано на рис. 3.21, сжимается с торца силой P. Длина стержня l  4 м, a  10
см. Определить значения критической и допускаемой нагрузок. Допускаемое напряжение    16 кН/см2, модуль Юнга E  2104 кН/см2. Решение задачи получить для
двух вариантов закрепления концов стержня: оба конца шарнирно оперты   1 ; оба
конца жестко защемлены   0,5 .
а)
P
б)
P
в)
Поперечное сечение
0,8а
X
0,8а
а
l=4м
Y
а = 10 см
Рис. 3.21
Решение
1. Определяем геометрические характеристики поперечного сечения стержня.
Площадь поперечного сечения стержня равна:
2
F  a 2  0,8a   0,36a 2 ;
F  0,36  10 2  36 см2.
Минимальный осевой момент инерции вычисляем по формуле:
4
a 4 0,8a 
I min  I x  I y 

 0,0492a 4 ;
12
12
I min  0,0492  10 4  492 см4.
Минимальный радиус инерции поперечного сечения стержня равен:
I
492
imin  min ;
imin 
 3,70 см.
F
36
2. Вычисляем гибкость стержня (  ).
Гибкость стержня равна:
для случая, когда оба конца стержня шарнирно оперты:
l
1  400

;

 108 ;
imin
3,70
если оба конца стержня жестко защемлены, то
l
0,5  400


 54 .
;
imin
3,70
3. По справочнику для стали марки Ст. 3 определяем коэффициент уменьшения
основного допускаемого напряжения (  ).
3. Темы, варианты и примеры решения задач
52
Для случая, когда оба конца стержня шарнирно оперты, по таблице находим, что
при гибкости   108 коэффициент уменьшения основного допускаемого напряжения
  0,491 .
  0,833 .
Если оба конца стержня жестко защемлены, то при   54
4. Определяем допускаемую нагрузку.
Условие устойчивости стержня имеет вид:
P
      .
F
Отсюда
P   F .
Допускаемая нагрузка равна:
для случая, когда оба конца стержня шарнирно оперты:
P  0,49116  36  283 кН.
для случая, когда оба конца стержня жестко защемлены:
P  0,833 16  36  480 кН.
5. Вычисляем критическую нагрузку.
Критическую нагрузку для шарнирно опертого по концам стержня вычисляем по
формуле Эйлера, поскольку гибкость стержня больше предельного значения:
  108  пр  100 .
Тогда
 2 EI min
 2  2  10 4  492
Pкр  Pэ 
P

 607 кН.
;
кр
 l 2
1  4002
Критическую нагрузку для жестко защемленного по концам стержня вычисляем
по формуле Ясинского:
Pкр  a  b F ,
так как гибкость стержня   54  пр  100 .
Для стального стержня a  31,0 кН/см2; b  0,114 кН/см2, тогда
Pкр  a  b F ;
Pкр  31,0  0,114  54  36  894 кН.
3.11. УДАР
Задача 11
На шарнирно опертую балку двутаврового поперечного сечения с высоты h падает
груз G (рис. 3.22). Найти наибольшее нормальное напряжение, возникающие в балке в момент удара, и оценить прочность балки при    16 кН/см2. Данные взять из табл. 3.13.
αl
h
2
h
1 G
l
l
Рис. 3.22
αl
G
3. Темы, варианты и примеры решения задач
53
Таблица 3.13
Исходные данные к задаче 11
Начальная буква фамилии,
имени, отчества
1
А, П
Б, Р
В, С
Г, Т
Д, У
Е, Ф
Ж, Х
З, Ц
И, Ч
К, Ш
Л, Щ
М, Э
Н, Ю
О, Я
Номер схемы
(рис. 3.22)
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
Номер
двутавра
3
12
12
14
14
16
16
18
18
20
20
22
22
24
24

4
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,2
0,3
0,4
0,5
0,6
0,7
0,8
l,
м
5
2,0
2,2
2,4
2,6
2,8
3,0
3,2
2,0
2,2
2,4
2,6
2,8
3,0
3,2
h,
cм
6
6
4
2
10
2
4
6
8
4
2
5
7
9
11
P,
кН
7
0,3
0,4
0,5
0,6
0,3
0,4
0,5
0,6
0,3
0,4
0,5
0,6
0,8
1,0
Пример 11
Найти наибольшее нормальное напряжение в шарнирно опертой двутавровой
балке, возникающее при падении на нее груза G  1 кН с высоты h  4 см (рис. 3.23).
Оценить прочность балки при    16 кН/см2. Двутавр № 20, l  3 м,   0,3 .
Решение
Наибольшее нормальное напряжение (  дин ), возникающее в балке в балке при
ударе, определяется по формуле:
 дин    ст ,
где  – коэффициент динамичности при ударе;  ст – наибольшее нормальное напряжение, которое возникло бы в балке при статическом приложении нагрузки, равной G.
Коэффициент динамичности при ударе вычисляется по формуле:
2h
  1 1
,
vст
где vст – статический прогиб балки в месте падения груза G, вызванный его статическим приложением.
1. Строим эпюру изгибающих моментов M x от силы G  1 кН, приложенной к
балке статически.
Изгибающий момент под сосредоточенной силой равен:
G  0,3l  0,7l
M xmax 
 0,21Gl ;
l
M xmax  0,21  1  3  0,63 кН·м.
2. В месте падения груза G прикладываем к балке единичную силу P  1 и строим от нее единичную эпюру изгибающих моментов M x .
Ордината этой эпюры под силой P  1 равна 0,21l или 0,63 м.
3. Определяем статический прогиб балки ( vст ) в месте падения груза G, перемножая полученные эпюры по правилу трапеций:
3. Темы, варианты и примеры решения задач
54
vст  M x  M x  
3
0,3l
2  0,21Gl  0,21l   0,7l 2  0,21Gl  0,21l   0,0147 Gl .
6 EI x
6 EI x
EI x
Для двутавра № 20 (ГОСТ 8239 – 72) осевой момент инерции I x  1840 см4, тогда
h = 4 см
vст  0,0147
а)
1 3003
 0,0108 см.
2 10 4 1840
G = 1 кН
Двутавр № 20
B
A
0,7l
l=3м
0,3l
RA = 0,7G
б)
G
RB = 0,3G
0,21Gl
МX
в)
R A  0,7
Р 1
R B  0,3
г)
0,21l
д)
MX
Рис. 3. 23
4. Коэффициент динамичности равен:
2h
24
  1 1
 1 1
 28,2 .
vст
0,0108
5. Вычисляем наибольшее статическое напряжение в балке ( Wx  184 см3):
63
M xmax
 ст 
 0,342 кН/см2.
 ст 
;
184
Wx
6. Вычисляем наибольшее динамическое напряжение в балке:
 дин  28,2  0,342  9,64 кН/см2.
 дин    ст ;
Прочность балки при ударе обеспечена, поскольку
 дин  9,64 кН/см2 <    16 кН/см2.
Литература
55
ЛИТЕРАТУРА
1. Феодосьев В. И. Сопротивление материалов. – М.: Наука, 1986. – 512 с.
2. Любошиц М. И., Ицкович Г. М. Справочник по сопротивлению материалов. –
Минск: Вышэйш. шк., 1969. – 464 с.
3. Дарков А. В., Шпиро Г. С. Сопротивление материалов. – М.: Высш. шк., 1989. – 622 с.
4. Пособие к решению задач по сопротивлению материалов / И. Н. Миролюбов,
С. А. Енгалычев, Н. Д. Сергиевский и др. – М.: Высш. шк., 1985. – 400 с.
5. Сопротивление материалов. Учеб. пособие / Н.А. Костенко, С.В. Балясникова,
Ю. Э. Волошановская и др.; Под ред. Н.А. Костенко – М.: Высш. шк., 2000. – 430 с.
6. Лейзерович Г.С. Введение в сопротивление материалов в вопросах и ответах:
Учебное пособие. – Комсомольск-на-Амуре: Государственное образовательное учреждение высшего профессионального образования «Комсомольскийна-Амуре гос. техн. ун-т», 2003. – 112 с.
Содержание
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ ................................................................................................................................................. 3
1.
РАБОЧАЯ ПРОГРАММА ...................................................................................................................... 4
2.1.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ .................................................................................................. 7
3.
ТЕМЫ, ВАРИАНТЫ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ .............................................................. 13
3.1.
РАСТЯЖЕНИЕ И СЖАТИЕ ............................................................................................................................................. 13
3.2.
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ ПРИ РАСТЯЖЕНИИ И СЖАТИИ ................................. 17
3.3.
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ ТЕЛА ......................................................................................................... 20
3.4.
КРУЧЕНИЕ КРУГЛОГО ВАЛА ....................................................................................................................................... 22
3.5.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ ............................................................................ 26
3.6.
ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ................................................................................................................................. 31
3.7.
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКИ ................................................................................................. 40
3.8.
ВНЕЦЕНТРЕННОЕ СЖАТИЕ .......................................................................................................................................... 43
3.9.
ИЗГИБ С КРУЧЕНИЕМ .................................................................................................................................................... 46
3.10.
УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ....................................................................................................................................... 50
3.11.
УДАР................................................................................................................................................................................... 52
ЛИТЕРАТУРА ................................................................................................................................................... 55
Учебное издание
ГРИГОРИЙ САМУИЛОВИЧ ЛЕЙЗЕРОВИЧ,
ВАЛЕРИЙ СЕРГЕЕВИЧ СИМОНОВ
ПРАКТИКУМ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Учебное пособие
Редактор Г.Н. Горькавая
ЛР № 020825 от 21.09.93
Подписано в печать 01.09.05.
Формат 60 х 84 1/8. Бумага 80 г/м2. Отпечатано на ризографе.
Усл. печ. л. 7,08. Уч.-изд. л. 4. Тираж. Заказ.
Институт новых информационных технологий Государственного образовательного
учреждения высшего профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
681013, Комсомольск-на-Амуре, пр. Ленина, 27.