2. Целочисленное линейное программирование

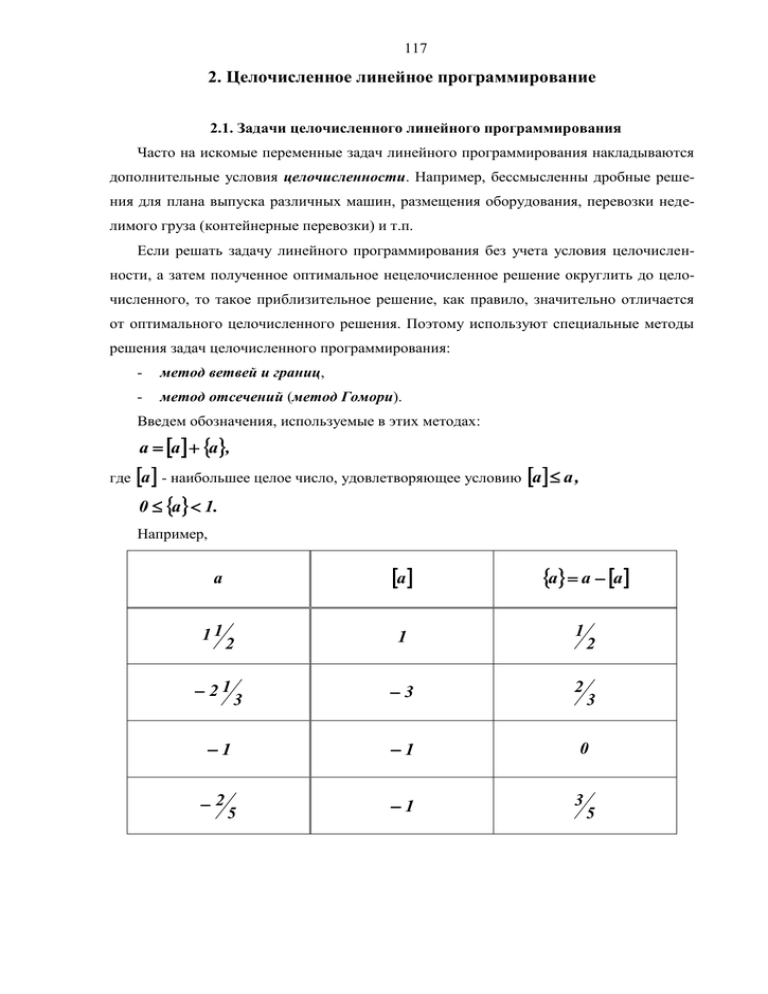
117
2. Целочисленное линейное программирование
2.1. Задачи целочисленного линейного программирования
Часто на искомые переменные задач линейного программирования накладываются
дополнительные условия целочисленности. Например, бессмысленны дробные решения для плана выпуска различных машин, размещения оборудования, перевозки неделимого груза (контейнерные перевозки) и т.п.
Если решать задачу линейного программирования без учета условия целочисленности, а затем полученное оптимальное нецелочисленное решение округлить до целочисленного, то такое приблизительное решение, как правило, значительно отличается
от оптимального целочисленного решения. Поэтому используют специальные методы
решения задач целочисленного программирования:
-
метод ветвей и границ,
-
метод отсечений (метод Гомори).
Введем обозначения, используемые в этих методах:
a  a   a,


где a - наибольшее целое число, удовлетворяющее условию a  a ,
0  a  1.
Например,
a 
a
11
2
21
3
1
2
5
a  a  a 
1
1
3
2
1
0
1
3
2
3
5
118
2.2. Метод ветвей и границ
Общая идея метода заключается в том, что сначала решается задача без учета
ограничений целочисленности. Если в результате решения этой ослабленной задачи

получено оптимальное нецелочисленное решение x j , то в интервале
x  x  x   1

j
j

j
нет допустимых целочисленных компонентов решения.
Поэтому допустимое целое значение x j должно удовлетворять одному из неравенств
 
 
x j  x j или x j  x j  1.
Введение этих условий в задачу с ослабленными ограничениями порождает две не
связанные между собой подзадачи. Таким образом, исходная задача разветвляется на
две подзадачи.
Затем решается каждая подзадача и процедура повторяется.
Нужно обратить внимание на то, что ветвление на подзадачи с помощью дополнительных ограничений приводит к уменьшению (увеличению) оптимального значения
максимизируемой (минимизируемой) целевой функции. Поэтому возникают следующие условия границ ветвления.
Границами ветвления каждой подзадачи являются:
1) получение целочисленного оптимума,
2) получение значения целевой функции, меньшего, чем значение целевой функции при ранее полученном целочисленном оптимуме.
▼
Пример
z  2x 1  3 x 2  max
при ограничениях
5 x 1  7 x 2  35 ,
4 x 1  9 x 2  36 ,
x 1  0 , x 2  0 - целые.
Решение
В первом варианте после решения подзадачи 5 дальнейшее ветвление подзадач 3 и
4 нецелесообразно, т.к. значения целевой функции, большего, чем 14, получить невозможно.
Выбор различных альтернатив ветвления приводит к разным последовательностям
подзадач, и следовательно, к различным количествам итераций, например, как показано
во втором варианте.
119
Первый вариант
№1
8
17
12
x1  3
17
6
x2  2
17
z  14
x2  2
x2  3
№2
№3
2
5
1
x1  4
5
x2  2
1
2
1
x1  2
4
x2  3
z  14
x1  5
№4
z  14
x1  5
x2  1
2
7
3
7
z  13
x1  4
№5
z  14
x1  4
x2  2
120
№1
Второй вариант
8
17
12
x1  3
17
6
x2  2
17
z  14
x2  2
x2  3
№2
№3
2
5
1
x1  4
5
x2  2
1
2
1
x1  2
4
x2  3
z  14
z  13
x1  3
x1  2
№4
№5
 3Нет
z  13
допустимых
x1  2
реше-
x2  3
ний
x2  4
▲
x1  5
№8
1
3
z  14
1
9
x2  1
x1  5
x2  3
№6
№7
z  12
x1  0
x2  4
z  13
x1  2
x2  3
2
7
3
7
x1  4
№9
z  14
x1  4
x2  2
121
Вопросы для самопроверки

Какие специальные методы используются для решения задач целочисленного
программирования?

Какая задача называется ослабленной?

Если получено оптимальное нецелочисленное решение, то в каком интервале
нет допустимых целочисленных компонентов решения?

Каким образом исходная задача разветвляется на две подзадачи в методе ветвей
и границ?

Какие условия являются границами ветвления каждой подзадачи в методе вет-
вей и границ?
Задания для самостоятельной работы
▼
Пример
Требуется решить методом ветвей и границ задачу:
5 x1  2 x 2  m a x
при ограничениях
x1 
x2  1 0 ,
4 x1  3 x 2  6 0 ,
x1 
x2  1 8 ,
x 1  0 , x 2  0  целые .
В ответе указать:
1) оптимальное решение x

2
 ( x1 , x 2 ) ;

2) оптимальное значение целевой функции z .
Решение
Графическое решение этой задачи без условия целочисленности (ослабленной задачи № 1):
122
x 1  x 2  10
6
6

,2
 12

7
7 

x 1  x 2  18
4 x 1  3 x 2  60
Оптимальная точка соответствует решению системы уравнений:
 x 1 - x 2  1 0 ,

4 x 1  3 x 2  6 0 .
Оптимальное решение:
x1  12
6
7
, x 2  2
6
7
, z 
410
4
 58
.
7
7
Т.к. оптимальное решение ослабленной задачи № 1 нецелочисленное, то она разветвляется на две подзадачи:
№1
z  58
4
7
x 1  12
x2  2
x 1  13
№2
6
7
6
7
x 1  12
№3
123
Графическое решение задачи № 2:
5 x1  2 x 2  m a x
при ограничениях
x1 
x2  1 0 ,
4 x1  3 x 2  6 0 ,
x1 
x2  1 8 ,
x1
 13 ,
x1  0 , x2  0 .
x 1  13
Задача № 2 не имеет допустимых решений.
Графическое решение задачи № 3:
5 x1  2 x 2  m a x
при ограничениях
x1 
x2  1 0 ,
4 x1  3 x 2  6 0 ,
x1 
x1
x2  1 8 ,
 12 ,
x1  0 , x2  0 .
124
x 1  x 2  10
x 1  12
Оптимальная точка соответствует решению системы уравнений:
 x 1 - x 2  1 0 ,

 x 1
12 .
Задача № 3 имеет оптимальное целочисленное решение.

Ответ: x 1  1 2
, x 2  2 , z   5 6 .
▲
1÷32. Решить методом ветвей и границ задачи линейного программирования 1÷32
x1
, x2
 целые .
из задания в п. 1.3 с дополнительными ограничениями
В ответе указать:



3) оптимальное решение x 2  ( x1 , x 2 ) ;

4) оптимальное значение целевой функции z .
33÷42. Решить задачу целочисленного программирования методом ветвей и границ,
учитывая целочисленность переменных:
max3 x 1  3 x 2 
4 x 1  5 x 2  20
33.
x 1  6 x 2  12
0  x1  5
0  x2  4
max3 x 1  2 x 2 
3 x 1  7 x 2  21
34.
x1  x2  4
0  x1  4
0  x2  3
125
max x 1  3 x 2 
3 x 1  4 x 2  12
35.
3 x1  2 x2  6
0  x1  4
0  x2  2
max4 x 1  x 2 
2 x1  3 x2  6
36.
4 x 1  9 x 2  18
0  x1  2
0  x2  3
max3 x 1  x 2 
4 x 1  3 x 2  18
37.
x1  2 x2  6
0  x1  5
0  x2  3
max x 1  2 x 2 
x1  x2  5
38.
3 x 1  8 x 2  24
0  x1  5
0  x2  3
max2 x 1  x 2 
5 x 1  2 x 2  30
39.
3 x 1  8 x 2  48
0  x1  6
0  x2  6
max3 x 1  2 x 2 
2 x1  3 x2  6
40.
x1  2 x2  2
0  x1  3
0  x2  3
max3 x 1  2 x 2 
2 x1  x2  6
41.
4 x1  3 x2  6
0  x1  3
1  x2  2
max x 1  2 x 2 
5 x 1  9 x 2  45
42.
x 1  3 x 2  12
0  x1  9
0  x2  4
43. Для улучшения финансового положения фирма приняла решение об увеличении выпуска конкурентоспособной продукции, для чего принято решение об установке
в одном из цехов дополнительного оборудования, занимающего 19/3 м площади. На
2
приобретение дополнительного оборудования фирма выделила 10 усл. ед., при этом
она может купить оборудование двух видов. Приобретение 1-ого комплекта оборудования 1ого вида стоит 1,0 усл. ед., 2-ого вида – 3 усл. ед. Приобретение одного комплекта оборудования 1-ого вида позволяет увеличить выпуск продукции в смену на 2
шт., а одного комплекта оборудования 2-ого вида – на 4 шт. Зная, что для установки
одного комплекта оборудования 1-ого вида требуется 2 м площади, а для оборудова2
ния 2-ого вида – 1 м площади, определить такой набор дополнительного оборудова2
ния, который дает возможность максимально увеличить выпуск продукции.
44÷48. Найти целочисленное решение задач.
   16 x
44. L x
2
1
 9 x 2  max
при ограничениях:
5 x 1  2 x 2  20
 x  x  6
.
 1
2
x 1 , 2  0  целые
  2x
45. L x
2
126
1
 3 x 2  min
при ограничениях:
2 x 1  x 2  9
3 x  4 x  3
.
 1
2
x 1 , 2  0  целые
  3x
46. L x
2
1
 x 2  max
при ограничениях:
2 x 1  3 x 2  6
2 x  3 x  3
.
 1
2
x 1 , 2  0  целые
  4 x
47. L x
2
1
 x 2  max
при ограничениях:
4 x 1  2 x 2  7
3 x  10 x  15 .
 1
2
x 1 , 2  0  целые
  x
48. L x
2
1
 x 2  max
при ограничениях:
x1  x 2  4


x1  3 x 2  9

.
 3 x 1  x 2  0
x 1 , 2  0  целые
49. Для приобретения оборудования по сортировке зерна фермер выделяет 34 усл.
ед. Оборудование должно быть размещено на площади, не превышающей 60 м .
2
Фермер может заказать оборудование двух видов: менее мощные машины А стоимостью 3 усл. ед., требующие производственной площади 3 м (с учетом проходов) и
2
обеспечивающие производительность за смену 2 т зерна, и более мощные машины В
стоимостью 4 усл. ед., занимающие площадь 5 м и обеспечивающие за смену сорти2
ровку 3 т зерна.
Определить оптимальный вариант приобретения оборудования, обеспечивающий
фермеру при данных ограничениях максимум общей производительности сортировки,
если он может пробрести не более 8 машин типа В.
127
2.3. Метод отсечений (Гомори)
Задача целочисленного линейного программирования решается методом Гомори.
Первый этап решения выполняется симплексным методом без учета целочисленности.

Если какой-либо компонент x j полученного оптимального решения оказывается
дробным, то составляется дополнительное ограничение, отсекающее дробную часть
решения и оставляющее в силе другие ограничения. Задача с расширенной таким путем
системой ограничений снова решается симплексным методом. Если и на этот раз получено нецелочисленное решение, то добавляется еще одно дополнительное ограничение
и т.д.
Выведем вид дополнительного ограничения, отсекающего дробную часть решения.
Пусть при решении ЗЛП без учета целочисленности
n
z   c j x j  max
j 1
при ограничениях
n
 ai j x j
j 1
 bi , i  1,m ;
x j  0,
j  1,n ;
получено оптимальное решение
x n  ( x 1 ,..., x q ,..., x n ),

в котором x q имеет наибольшую дробную часть.
Берем из ограничений любое p -ое неравенство с переменной x q
n
ap j xj
j 1
 bp .
Составляем уравнение, в котором эта переменная x q выражена линейно через
остальные переменные:
n
x q  b p/   a p/ j x j ,
j 1
jq
128
где b p 
/
bp
, a p/ j 
a pq
ap j
a pq
при j  1 ,( q  1 ) и j  ( q  1 ), n .
Поскольку x q должно быть целым, то
b   a
/
p
n
 j 1
/
pj

x j  - целое,

где 
 - дробная часть числа.
А т.к. все x j должны быть целыми и неотрицательными, то
b   a x
/
p
n
j 1
jq
/
pj
 a p/ j  x j
n
j 1
jq
j
 0 , или
 b p/ .
Это неравенство и представляет собой дополнительное ограничение.
▼
Пример
На приобретение оборудования выделено 20 млн. руб., а на его размещение – 38 кв.
м. Можно закупить станки А, каждый стоимостью 5 млн. руб., производительностью 7
тыс. деталей в смену и требующий для размещения 8 кв. м. или станки Б, каждый стоимостью 2 млн. руб., производительностью 3 тыс. деталей в смену и размещающийся на
4 кв. м. Требуется выбрать вариант приобретения оборудования, обеспечивающий максимальную производительность при ограничениях по денежным средствам и по производственной площади.
Решение
Пусть количество закупаемых станков А равно x 1 , а Б - x 2 .
Тогда модель задачи имеет вид:
z  7x 1  3 x 2  max
при ограничениях
5 x 1  2 x 2  20 ,
8 x 1  4 x 2  38 ,
x 1  0 , x 2  0 - целые.
129
В канонической форме:
z  7x 1  3 x 2  max
при
5 x1  2 x2  x3
8 x1  4 x2 
 20 ,
x 4  38.
Решая симплексным методом получаем на последней итерации:
i
Б
План
x1
x2
x3
x4
1
x1
x2
1
1
0
1
-0,5
7,5
29,5
0
0
1
0
-2
1
1,25
0,25
2
Оптимальное решение: x

4
 ( x 1 , x 2 , x 3 , x 4 )  ( 1; 7 , 5 ; 0 ; 0 ).
Поскольку требование целочисленности не выполнено для x 2 , составляем уравнение по строке i  2 :
x 2  2 x 3  1 ,25 x 4  7 ,5.
Дополнительное ограничение будет иметь вид:
1 x 2   2 x 3  1 ,25 x4  7 ,5, или
0  x 2  0  x 3  0 ,25 x 4  0 ,5 ,
или в канонической форме
0 ,25 x 4  x 5  0 ,5.
Решаем симплексным методом задачу
z  7x 1  3 x 2  max
при
5 x1  2 x 2  x 3
8 x1  4 x 2 
 20 ,
x4
 38 ,
0 ,25 x 4  x 5  0 ,5.
Получим целочисленное оптимальное решение:
x 5  ( x 1 , x 2 , x 3 , x 4 , x 5 )  ( 2 ; 5 ; 0 ; 2 ; 0 ).
▲
130
Вопросы для самопроверки

Что представляют собой этапы решения задачи целочисленного линейного про-
граммирования методом Гомори?

Как выводится вид дополнительного ограничения, отсекающего дробную часть
решения?
Задания для самостоятельной работы
1. В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено 19,3 м
2
площади. На приобретение оборудования пред-
приятие может израсходовать 10 тыс. у.е., при этом оно может купить оборудование
двух видов. Комплект оборудования первого вида стоит 1000 у.е., а второго вида – 3000
у.е. Приобретение одного комплекта оборудования первого вида позволяет увеличить
выпуск продукции в смену на 2 ед., а одного комплекта оборудования второго вида – на
3 ед. Зная, что для установки одного комплекта оборудования первого вида требуется 2
м 2 площади, а оборудования второго вида – 1 м 2 площади определить такой набор
дополнительного оборудования, который дает возможность максимально увеличить
выпуск продукции.
2. Найти целочисленное решение задачи
  4 x
Lx
2
1
 3 x1  2 x2

 x1  4 x2
 3 x 1  3 x 2
x1 , 2 , 3  0 
 5 x 2  x 3  max при ограничениях:
 10
 11
.
 13
целые
3. Найти целочисленное решение задачи
  x
Lx
2
1
 2 x 2  x 3  3 x 4  max при ограничениях:
 x 1  12 x 2  4 x 3  x 4  34
3 x  4 x  2 x  x  22 .
2
3
4
 1
x 1 , 2 , 3 , 4  0  целые
4. Фирма выпускает три вида изделий А, Б, В, причем плановый сменный выпуск
составляет 9 шт. изделия А, 7 шт. изделия Б, 6 шт. изделия В.
Сменные ресурсы: 51 ед. производственного оборудования, 48 ед. сырья, 67 ед.
131
электроэнергии, их расход на одно изделие дан в таблице.
Ресурсы
Оборудование
Сырье
Электроэнергия
Изделие А
3
1
3
Изделие Б
2
4
3
Изделие В
0
0
1
Прибыль от реализации изделий А – 40 усл. ед.,Б – 50 усл. Ед., В – 10 усл. ед.
Определить, сколько изделий каждого вида надо производить, чтобы получить максимальную прибыль от выпускаемых сверх плана изделий.
5. Три типа самолетов следует распределить между четырьмя авиалиниями. В таблице приведены данные месячного объема перевозок каждым самолетом на каждой линии и соответствующих эксплуатационных расходов.
Тип
Число
самолета самолетов
1
2
3
Месячный объем перевозок
одним самолетом по авиалиниям
50
20
30
15
30
25
10
25
50
20
10
30
50
17
45
Эксплуатационные расходы на
один самолет по авиалиниям
15
70
40
20
28
70
25
15
40
Распределить самолеты по линиям так, чтобы при минимальных суммарных эксплуатационных расходах перевести по каждой из четырех авиалиний не менее 300, 200,
1000 и 500 ед. груза соответственно.
6÷15. Дана задача линейного программирования
  c x
Lx
2
1
1
 c 2 x 2  max min 
при ограничениях
a 1 1 x 1  a 1 2
a x  a
21
1
22
a x  a
32
 31 1

x2
x2
x2
x1 ,2
 b1
 b2
.
 b3
 0
Методом ветвей и границ найти максимальное и минимальное целочисленные решения задач.
Решить задачу методом Гомори, принимая по своему усмотрению стремление целевой функции к максимальному или минимальному значениям.
40
45
65
132
Значения коэффициентов целевой функции и системы ограничений
№
варианта
6
7
8
9
10
11
12
13
14
15
c1
c2
a11
4
3
-1
-3
2
4
-3
-3
5
-2
5
2
-1
-5
3
3
-2
4
-2
3
6
8
7
4
8
10
8
15
9
3
a1 2
4
5
10
6
6
7
9
8
12
-10
b1
a2 1
37
42
68
41
51
73
75
110
118
31
5
5
9
6
-5
-5
7
5
-2
6
a2 2
6
7
7
4
7
2
-5
10
4
13
b2
a31
43
33
65
38
34
9
32
53
-7
75
2
4
3
2
-2
2
2
2
10
10
a3 2
3
2
2
4
6
5
8
12
5
2
b3
5
5
7
5
7
12
17
25
52
21
133
3. Динамическое программирование
3.1. Задача динамического программирования
Методы динамического программирования применяются для повышения эффективности вычислений при решении задач математического программирования путем их
разложения (декомпозиции) на менее сложные подзадачи. Как правило, решение общей задачи математического программирования представляется последовательностью его этапов. Каждому такому этапу ставится в соответствие частная подзадача.
Решение частной подзадачи осуществляется с учетом рекуррентного соотношения,
отражающего принцип оптимальности Беллмана: каковы бы ни были предыдущее
состояние и принятое предыдущее решение, последующие решения должны составлять оптимальную стратегию относительно состояния, возникшего в результате
предыдущего решения.
Представим модель динамического программирования на некотором общем примере.
Рассмотрим задачу распределения капиталовложений. Для реконструкции n заводов выделено y 0 капиталовложений. Если i -ому заводу выделяется x i капиталовложений, то на нем увеличивается выпуск продукции до величины z i ( x i ) . Требуется
найти вариант распределения капиталовложений, при котором суммарное увеличение
выпуска продукции всеми n заводами максимально.
Обозначим:
z 1...n ( y0 ) - суммарное увеличение выпуска продукции всеми n заводами при распределении между ними y 0 капиталовложений,
x n  ( x 1 , x 2 ,..., x k ,..., x n ) - распределение по n заводам капиталовложений.
Тогда задачу можно представить в виде:
z 1...n  y 0   max  z i ( x i )
n
x
n
i 1
при ограничениях
n
 x i  y0 ,
i 1
x i  0 , i  1,n .
При любом представлении функций z i ( x i ) , i  1 , n , решение этой задачи сопря-
134
жено со значительными трудностями. Поэтому представим ее моделью динамического
программирования.
Этап 1.
Если количество заводов n  1 , то
z 1  y   max z 1 ( x 1 ) .
0  x1  y
Этап 2.
Если количество заводов n  2 , то максимальное увеличение выпуска продукции
всеми ими соответствует максимальному варианту суммарного увеличения выпуска
продукции вторым заводом и остальными заводами (первым заводом) при различном
распределении y капиталовложений:
z12 ( y )  maxz 2 ( x 2 )  z1 ( y  x 2 ).
0  x2  y
Этап k.
Продолжая аналогичные рассуждения, получим общее рекуррентное соотношение:
z1...k ( y )  maxz k ( xk )  z1...( k 1 ) ( y  xk ).
0  xk  y
Полученное рекуррентное соотношение называется уравнением Беллмана и позволяет заменить исходную задачу на максимум функции n переменных задачей на
условный максимум функции одной переменной на n этапах.
3.2. Метод решения задач динамического программирования
В рассматриваемой выше задаче распределения капиталовложений оптимальная

стратегия представляет собой последовательность оптимальных значений z 1...n( y0 ) ,

z1...(n
-1) ( y ) ,
…,
z 1 ( y ) ,
которая
определяет
оптимальное
решение
x n  ( x1 , x 2 ,..., x n ) .
Поэтому сначала (прямой прогон) отыскивают последовательно функции Беллмана
z 1 ( y ) , z 12 ( y ) , …, z1...(n-1) ( y ) , z 1...n ( y0 ) как функции различных параметров y
соответственно.

Затем (обратный прогон) определяется оптимальное значение z 1...n( y0 ) и соответствующее
ему
оптимальное
значение
x n .
Затем
оптимальное
значение
135



z1...(n
-1) ( y0  x n ) и соответствующее ему оптимальное значение x n - 1 . Продолжая этот
процесс,
получим
оптимальные
z1 ( y0  xn  xn1  ...  x 2 )
и
значения
соответствующие



z1...(n
- 2) (y0  x n  x n1 ) ,
им
оптимальные
…,
значения
x n 2 ,..., x1 , т.е. оптимальный план.
▼
Пример
Рассмотрим решение конкретной задачи распределения капиталовложений. Для
реконструкции трех заводов выделено 5 млн. руб. капиталовложений. Увеличение выпуска продукции (в млн. руб.) после реконструкции в зависимости от выделенного i -


ому заводу i  1, 3 объема капиталовложений x обозначим z i ( x ) и зададим в таблице:
x
z1 ( x )
z2 ( x )
z3 ( x )
1
2
3
4
5
5
12
16
21
23
7
10
14
20
25
6
13
18
21
22
Необходимо найти вариант распределения капиталовложений, при котором суммарное увеличение выпуска продукции на трех заводах максимально.
Для решения задачи используем алгоритм динамического программирования.
Сначала (прямой прогон) рассчитаем функции, показывающие суммарное увеличение выпуска продукции на k заводах, по рекуррентному соотношению:
z 1...k ( y )  max z k ( x k )  z 1...( k 1 ) ( y  x k ).
0  xk  y
Для k  1 , т.е. при выделении объема капиталовложений y одному заводу
(например, первому) функция совпадает с z 1 ( x ) .
Рассчитаем функцию z 12 :


z ( 0 )  z ( 1 ) при x  0 
0 5
z 12 ( 1 )  max
 z 2 ( 1 )  z 1 ( 0 ) при x 2  1  max 7  0  7 ,
 2

1
2
136


 z 2 ( 0 )  z 1 ( 2 ) при x 2  0 

 0  12 

z 12 ( 2 )  max z 2 ( 1 )  z 1 ( 1 ) при x 2  1   max 7  5   12 ,


10  0 

 z 2 ( 2 )  z 1 ( 0 ) при x 2  2 

z 2 ( 0 )  z 1 ( 3 )

z 12 ( 3 )  max z 2 ( 1 )  z 1 ( 2 )
z (2 ) z (1)
z 2 ( 3 )  z 1 ( 0 )
 2
1
при
при
при
при
x2
x2
x2
x2
 0  1 6
 0
 1   max 7  1 2   19 ,
1 0  5 
 2


 3
1 4  0 
z 2 ( 0 )  z 1 ( 4 )
 z 2 ( 1 )  z 1 ( 3 )
z 12 ( 4 )  max z 2 ( 2 )  z 1 ( 2 )
z 2 ( 3 )  z 1 ( 1 )
 z 2 ( 4 )  z 1 ( 0 )
при
при
при
при
при
x2
x2
x2
x2
x2
 0  2 1
 0
 7  1 6
 1 


 2   max 1 0  1 2   23 ,
 3
1 4  5 
 4 
2 0  0 
z 2 ( 0 )  z 1 ( 5 )
z 2 ( 1 )  z 1 ( 4 )
z 2 ( 2 )  z 1 ( 3 )

z 12 ( 5 )  max z 2 ( 3 )  z 1 ( 2 )
z 2 ( 4 )  z 1 ( 1 )
z 2 ( 5 )  z 1 ( 0 )

при
при
при
при
при
при
x2
x2
x2
x2
x2
x2
 0
 0  2 3
 1
 7  2 1
 2 


 3   max 1 0  1 6   2 8 .
1412
 4
2 0  5 
 5


2 5  0 

Рассчитаем функцию z 123 ( y0 )  z 123 ( 5 ) , т.к. только при полном выделении капиталовложений всем заводам достигается максимальное суммарное увеличение выпуска ими продукции:
 z 3 ( 0 )  z 12 ( 5 )
 z 3 ( 1 )  z 12 ( 4 )
 z ( 2 )  z 12 ( 3 )
z 123 ( 5 )  max 3
z (3) z (2)
 z 3 ( 4 )  z 12 ( 1 )
12
 3
z
(
5
)

z
12 ( 0 )
 3
при
при
при
при
при
при
x3
x3
x3
x3
x3
x3
 0  2 8
 0
 6  2 3
 1


 2
 max 1 3  1 9   3 2 .

3
1812
2 1  7 
 4



 5
2 2  0 
Затем (обратный прогон) находим, что максимальное суммарное увеличение выпуска продукции не трех заводах z 123 ( 5 )  32 млн. руб. При этом третьему заводу
выделяется 2 млн. руб. капиталовложений, а остальным двум –3 млн. руб.
При выделении двум оставшимся заводам 3 млн. руб. капиталовложений максимальное суммарное увеличение выпуска продукции на них z 12 ( 3 )  19 млн. руб. При
этом второму заводу выделяется 1 млн. руб. Тогда первому заводу выделяется оставшиеся 2 млн. руб. капиталовложений.
Итак, максимальное суммарное увеличение выпуска продукции на трех заводах 32
137
млн.
руб.
при
оптимальном
распределении
капиталовложений
x 3  ( x 1 , x 2 , x 3 )  ( 2 ; 1 ; 2 ) млн. руб.
▲
3.3. Решение задачи линейного программирования
методом динамического программирования
Рассмотрим общую задачу линейного программирования:
z  c1 x 1  c 2 x 2  ...  c n x n  max
при ограничениях
a11 x1  a12 x 2 ...  a1 n x n  b1 ,
a 21 x 1  a 22 x 2  ...  a 2 n x n  b2 ,
…………………………………...
a m 1 x 1  a m 2 x 2  ...  a mn x n  bm ,
x1 ,
x 2 ,..., x n  0.
Задача линейного программирования относится к классу задач распределения:
распределяются ресурсы b1 , b2 ,...,bm по уровням производственной деятельности
x 1 , x 2 ,..., x n с целью максимизации показателя z.
Общая задача линейного программирования может быть представлена в виде модели динамического программирования. Для этого каждый вид производственной деятельности j ( j  1 , n ) следует интерпретировать как этап, а каждый уровень производственной деятельности x j представляет варианты решения на этапе j . Так как всего имеется m видов ресурсов, то рекуррентное соотношение должно строиться относительно m -мерного вектора y
m j
 (y 1 j , y 2 j ,..., y mj ) , компоненты которого выра-
жают объемы ресурсов 1,2,...,m , распределенных на j -ом этапе. Тогда рекуррентное
соотношение примет вид:
z1...j ( y1 j , y 2 j ,..., ym j ) 
 max c j x j  z1...( j  1 )  y1 j  a1 j x j , y 2 j  a 2 j x j ,..., ym j  am j x j .
0  ai j x j  yi j ,
i  1 , 2 ,...,m
При j  n имеем yi n  bi , i  1, m , и z 1...n b1 , b2 ,...,bm  
138
 max c n x n  z 1...n1  b1  a 1 n x n , b2  a 2 n x n ,...,bm  a m n x n .
0  a i n xn  bi ,
i  1 ,m
Таким образом, задача линейного программирования может быть решена методом
динамического программирования.
Вопросы для самопроверки

Каким образом методы динамического программирования повышают эффек-
тивность вычислений при решении задач математического программирования?

В чем выражается принцип оптимальности Беллмана?

Для какого преобразования исходной задачи строится рекуррентное соотноше-
ние?

Какие этапы содержит метод решения задач динамического программирования?

Что интерпретируется как этап при составлении рекуррентного соотношения
для решения задачи линейного программирования методом динамического программирования?
Задания для самостоятельной работы
▼
Пример
Требуется решить следующую задачу о загрузке (задачу о рюкзаке) методом динамического программирования.
Автомобиль загружается предметами n различных типов. Каждый предмет i -ого
типа имеет вес w i и стоимость v i , i  1 , n . Максимальная грузоподъемность автомобиля w . Требуется определить максимальную стоимость груза, вес которого не должен
превышать максимальной грузоподъемности.
Вспомогательные пояснения
Если обозначить через x i количество загружаемых предметов типа i , то задача
принимает следующий вид:
z  v 1 x 1  v 2 x 2  ...  v n x n  max
139
при ограничениях
w 1 x 1  w 2 x 2  ...  w n x n  w ,
x1 ,
x n  0 - целые.
x 2 , ...,
Если отбросить условие целочисленности, то решение задачи можно найти симплексным методом.
Используем для решения исходной задачи метод динамического программирования.
Разобьем решение задачи на n этапов, каждый из которых соответствует поиску
количества загружаемых предметов одного типа.
Сформулируем рекуррентное соотношение. Для этого обозначим через y вес загружаемых предметов, 0  y  w .
Тогда стоимость загруженных предметов 1-ого типа с суммарным весом y определяется как:
z1 ( y ) 
max
 y 
x1 0 ,1 ,..., 
 w1 
v1 x1 .
Стоимость загруженных предметов 1-ого и 2-ого типов с суммарным весом y
определяется как:
z12 ( y ) 
max
 y 
x2 0 ,1 ,...,

 w2 
v 2 x2  z1  y  w2 x2 .
Стоимость загруженных предметов всех трех типов с суммарным весом y определяется как:
z 123 ( y ) 
max
 y 
x 3  0 ,1 ,...,

 w3 
v 3 x 3  z 12  y  w 3 x 3 .
В общем случае, стоимость загруженных предметов с 1-ого по k-ый тип с суммарным весом y загруженных предметов определяется как:
z 1...k ( y ) 
max
 y 
xk 0 ,,1 ,...,

 wk 
v
k
x k  z 1...( k 1 )  y  w k x k .
После того, как определено число этапов и составлено рекуррентное соотношение
задача решается стандартным образом.
Рассмотрим конкретный пример задачи загрузки: w  5 и всего имеются три типа
предметов, числовые сведения о которых приведены в таблице:
140
i
wi
vi
1
2
3
2
3
1
65
80
30
Решение
Используем для расчетов выведенное рекуррентное соотношение:
z 1...k ( y ) 
max
 y 
xk 0 ,1 ,...,

 wk 
v
k
x k  z 1...( k 1 ) ( y  w k x k ).
Рассчитаем по исходным данным:
z1 ( 0 )  0
z1 ( 1 )  0
z 1 ( 2 )  65
z 1 ( 3 )  65
z 1 ( 4 )  130
z 1 ( 5 )  130
z 12 ( 0 )  0
z 12 ( 1 )  0
z 12 ( 2 )  65
80  0  z 1 ( 3  3  0 )  max 0  6 5   80
z 12 ( 3 )  max 


8 0  0 
 3  80  1  z 1 ( 3  3  1 


x 2 0 ,  
3
80  0  z 1 ( 4  3  0   max 0  1 3 0   130
z 12 ( 4 )  max 


8 0  0 
 4  80  1  z 1 ( 4  3  1 


x 2 0 ,  
3
80  0  z 1 ( 5  3  0 )  max 0  1 3 0   145
z 12 ( 5 )  max 


8 0  6 5 
 5  80  1  z 1 ( 5  3  1 ) 


x 2 0 ,  
3
z123 ( 0 )  0
z123 ( 1 )  30
 0  6 5
 30  0  z 12 ( 2  1  0 ) 


z 123 ( 2 )  max  30  1  z 12 ( 2  1  1 )   max 3 0  0   65
x 3  0 ,1 , 2
 30  2  z 12 ( 2  1  2 )
6 0  0 
 0  8 0
 30  0  z 12 ( 3  1  0 ) 


 30  1  z 12 ( 3  1  1 ) 
z 123 ( 3 )  max 
 max 3 0  6 5   95

60 0
x 3 0 ,1 , 2 , 3 30  2  z 12 ( 3  1  2 )
 30  3  z ( 3  1  3 )




12
9 0  0 
141
 0  1 3 0
 30  0  z 12 ( 4  1  0 ) 
 3 0  8 0
 30  1  z 12 ( 4  1  1 ) 


z 123 ( 4 )  max  30  2  z 12 ( 4  1  2 )  max 6 0  6 5   130
x 3  0 ,1 , 2 , 3 , 4
 30  3  z 12 ( 4  1  3 )
 90
0
 30  4  z 12 ( 4  1  4 )
1 2 0 
0 
 0  1 4 5
 30  0  z 12 ( 5  1  0 ) 
 3 0  1 3 0
 30  1  z 12 ( 5  1  1 ) 
 6 0  8 0 


z 123 ( 5 )  max  30  2  z 12 ( 5  1  2 )  max
 160
x 3 0 ,1 , 2 , 3 ,4 ,5 30  3  z 12 ( 5  1  3 )
9 0  6 5
 30  4  z ( 5  1  4 )


1
2
0

0
12
 30  5  z ( 5  1  5 )




12
1 5 0 
0 
При максимальной стоимости груза 160 должен быть загружен один предмет 3-его
типа стоимостью 30. Следовательно, стоимость загружаемых предметов 1-ого и 2-ого
типов равна 130. Такой стоимости соответствует отказ от загрузки предметов 2-ого типа.
Тогда
должны
быть
загружены
два
предмета
1-ого
типа.
В
итоге,
x 3  ( 2 ; 0 ; 1 ) .
Ответ: максимальная стоимость груза 160.
▲
1. Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех
предприятиях, принадлежащих фирме.
Для расширения производства совет директоров выделяет средства в объеме 120
млн р. с дискретностью 20 млн р. Прирост выпуска продукции на предприятиях зависит
от выделенной суммы, его значения представлены предприятиями и содержатся в таблице.
Выделенные
средства,
млн р.
20
40
60
80
100
120
Предприятие
№1
8
16
25
36
44
62
Прирост выпуска продукции, млн р.
Предприятие
Предприятие
№2
№3
10
12
20
21
28
27
40
38
48
50
62
63
Предприятие
№4
11
23
30
37
51
63
Найти распределение средств между предприятиями, обеспечивающее максималь-
142
ный прирост выпуска продукции, причем на одно предприятие можно осуществить не
более одной инвестиции.
2. Торговая фирма располагает 5 автолавками, которые могут быть направлены в
воскресный день в 3 населенных пункта. Считается, что товарооборот фирмы зависит
лишь от количества и ассортимента направляемых товаров и определяется числом посланных в тот или иной населенный пункт машин.
Среднее значение товарооборота в тыс. р. в каждом из населенных пунктов задано
в таблице.
Товарооборот в населенных пунктах, тыс. р.
1
2
3
15
12
18
24
20
23
30
31
29
37
38
36
41
42
39
Количество
автолавок
1
2
3
4
5
Найти оптимальную стратегию фирмы в распределении автолавок по населенным
пунктам, максимизирующую общий товарооборот.
3. В таблице указан возможный прирост выпуска продукции четырьмя плодовоконсервными заводами области в млн р. при осуществлении инвестиций на их модернизацию с дискретностью 50 млн р., причем на один завод можно осуществить только
одну инвестицию.
Инвистиции,
млн р.
50
100
150
200
1
25
60
100
140
Прирост выпуска продукции, млн р.
Заводы
2
3
30
36
70
64
90
95
122
130
4
28
56
110
142
Составить план распределения инвестиций между заводами области, максимизирующий общий прирост выпуска продукции.
4. В трех областях необходимо построить 5 предприятий по переработке сельскохозяйственной продукции одинаковой мощности.
143
Функция расходов g i  x  , характеризующая величину затрат на строительство и
эксплуатацию в зависимости от количества размещаемых предприятий в i -ой области,
приведена в таблице.
x
g1 x 
g 2 x 
g 3 x 
1
8
2
14
3
22
4
29
5
34
10
17
18
27
31
11
16
15
26
31
Разместить предприятия таким образом, чтобы обеспечить минимальные суммарные затраты на их строительство и эксплуатацию.
5÷14. Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех
предприятиях, принадлежащих фирме.
Для модернизации предприятий совет директоров инвестирует средства в объеме
250 млн р. с дискретностью 50 млн р. Прирост выпуска продукции зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таблице.
Инвестиции,
млн. р.
Прирост выпуска продукции, млн. р.
Предприятие 1
Предприятие 2
Предприятие 3
Предприятие 4
50
a11
a1 2
a1 3
a1 4
100
a21
a2 2
a2 3
a2 4
150
a31
a3 2
a3 3
a3 4
200
a4 1
a4 2
a4 3
a4 4
250
a5 1
a5 2
a5 3
a5 4
Найти распределение инвестиций между предприятиями, обеспечивающее фирме
максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить только одну инвестицию.
144
Значения коэффициентов условия задачи
№
варианта
5
6
7
8
9
10
11
12
13
14
a11
5
8
11
10
12
21
22
23
25
15
a1 2
7
10
12
9
13
20
23
24
26
12
a1 3
6
7
10
7
11
22
24
25
27
17
a1 4
4
10
11
8
11
23
21
22
28
13
a2 1
9
13
16
15
17
30
31
32
34
32
a2 2
10
12
15
16
15
28
30
31
33
30
a2 3
8
14
17
13
16
31
32
33
35
33
a2 4
11
13
14
14
18
29
29
30
35
31
a31
21
22
23
24
23
42
43
44
46
39
a3 2
20
21
24
22
25
41
41
43
46
38
a3 3
21
22
22
20
21
40
42
42
45
40
a3 4
19
23
25
21
22
41
40
41
44
37
a4 1
33
31
32
33
34
51
52
53
57
46
a4 2
34
38
31
34
33
52
53
52
58
45
a4 3
32
29
32
31
35
53
51
54
56
47
a4 4
35
30
30
32
34
50
53
55
55
44
a5 1
38
39
38
40
42
62
63
70
78
52
a5 2
39
40
39
39
41
63
64
72
77
54
a5 3
40
38
40
41
43
61
65
71
79
60
a5 4
41
41
38
40
44
64
66
73
80
63
15. Самолет грузоподъемностью 83 условных единицы груза предполагается загрузить четырьмя типами груза. Массы и стоимость грузов i-ого типа в условных единицах
заданы в таблице.
Массы и стоимости груза i-ого типа (в условных единицах)
Показатель,
Тип груза, i
условные
1
2
3
4
единицы
Масса
10
16
22
24
Стоимость
20
50
85
96
Необходимо загрузить самолет таким образом, чтобы общая ценность груза была
максимальной.
145
4. Нелинейное программирование
4.1. Задачи нелинейного программирования
К классу нелинейного программирования относятся задачи, в которых либо целевая функция, либо ограничения, либо и то и другое нелинейны.
Общая формулировка задачи:
z  ( x
n
)  max
при ограничениях
gi ( x
x
n
n
)  0 , i  1, m ;
0.
Функция
 (x
n
) имеет единственный экстремум, если она выпукла (задачи вы-
пуклого программирования).
Необходимым и достаточным условием выпуклости функции
 (x
n
) является
положительная полуопределенность матрицы, составленной из вторых частных производных этой функции:
  2
 2
 2 
 2

...

x

x

x

x

x
 1
1
2
1
n 
  2
 2
 2 
...

.
2

x

x

x
x

x
2
1
2
n
2


......................
 ..........

2
 2
 2 
  
 x x x x ... x 2 
n
2
n 
 n 1
Для выполнения указанного условия положительной полуопределенности требуется, чтобы были неотрицательными все главные миноры этой матрицы, т.е. главные
миноры k -ого порядка ( k  1, n) , являющиеся определителями, составленными из
элементов первых k строк и первых k столбцов рассматриваемой матрицы.
Экстремум целевой функции может достигаться как на границе области допустимых решений, так и внутри этой области.
Условиями экстремума функции (x
x
n
являются:
n
) без учета ограничений на ее аргументы
146
-
необходимое условие

 0 , i  1, n ;
x i
-
достаточное условие предполагает, что в некоторой окрестности оптимально-
го плана x

n
вторая производная не изменяет знак
n
 2
   2  2 
j1 x j
j 1
n
 2
 x x .
i 1
j
i
n
i j
Вид экстремума определяется знаком второй производной в экстремальной точке:
-
   0 , то функция ( x
если  x   0 , то функция ( x
если   x

n
n
) имеет в точке x n максимум;

n
n
) имеет в точке x n минимум.
Таким образом, проверка необходимых условий экстремума целевой функции позволяет найти оптимальную точку, а проверка достаточных условий экстремума – определить максимум или минимум достигает целевая функция в оптимальной точке. Однако найденная оптимальная точка безусловного экстремума целевой функции может
не являться решением исходной задачи (условного экстремума) нелинейного программирования, т.к. для нее не будут выполняться ограничения этой задачи.
4.2. Решение задачи нелинейного программирования
методом множителей Лагранжа
Введем вектор λ m  ( λ1 , λ2 ,..., λm ) и составим из целевой функции
функций ограничений g i ( x
L( x
n
, m )  ( x
n
( x n ) и
) , i  1 , m , функцию Лагранжа:
m
n
)   i gi ( x
i 1
n
).
Таким приемом исходная задача на условный экстремум функции
дится к задаче на безусловный экстремум функции L(x
n
Тогда необходимыми условиями экстремума служат:
,
m
).
 (x
n
) сво-
147
m
g i

 L



 0 , j  1, n ,

i
 x
x j i  1 x j
j
 L

 g i ( x n )  0 , i  1, m .
  i
Таким образом, образуется система n  m  алгебраических уравнений с n  m 
переменными.
Достаточным условием экстремума в рассматриваемой задаче служит постоянство знака второй производной
 (x n ) в окрестности экстремальной точки, а ее знак
определит вид экстремума:
при
   0 - минимум,
при
   0 - максимум.
В общем случае необходимые и достаточные условия экстремума определяются
теоремой Куна-Таккера. Ее смысл сводится к следующему. Точка (x
ется седловой точкой функции L(x
n
,
m
) , если для всех x
n

n
, m ) явля-
 0 и  m  0 вы-
полняется условие:
L(x n ,  m )  L( x *
L(x
n
,
m
n
, *
m
)  L( x n , m ) ,
т.е.
в
) достигается одновременно минимум по x
седловой
n
точке
и максимум по
функцией
m .
Вопросы для самопроверки

Какие задачи относятся к классу нелинейного программирования?

При каком условии функция от n переменных имеет единственный экстремум?

Что является необходимым и достаточным условием выпуклости функции от n
переменных?

Что необходимо для выполнения условия положительной полуопределенности?

Какие условия являются условиями экстремума функции от n переменных без
учета ограничений на ее аргументы?

Чем определяется вид экстремума функции от n переменных?
148

Всегда ли найденная оптимальная точка безусловного экстремума целевой
функции является решением исходной задачи (условного экстремума) нелинейного
программирования?

Как составляется функция Лагранжа из целевой функции и функций ограниче-
ний?

К какой задаче сводится исходная задача на условный экстремум методом мно-
жителей Лагранжа?

Как в общем случае определяются теоремой Куна-Таккера необходимые и до-
статочные условия экстремума?
Задания для самостоятельной работы
▼
Пример
1. Исследовать на выпуклость функцию
 (x 1 , x 2 )  2 x 13  5 x 22 ,
x1  0 , x 2  0 .
Решение
Вычислим необходимые для этого производные:


 2
2
 6 x1 ,
 10 x 2 ,
 12 x 1 ,
x 1
x 2
x 12
 2
 10 ,
x 22
 2
 0,
x 1 x 2
 2
0.
x 2 x 1
Составим матрицу:
  2
 2 
 2

 x 1 x 1 x 2    12 x 1 0 


  2
 2    0 10 

2 
 x 2  x 1 x 2 
Главные миноры:
M 1  12 x 1 ,
M 2  12 x 1 0  120 x 1 .
0 10
149
Главные миноры неотрицательны при x 1  0 и x 2  0 , следовательно, заданная
функция выпукла в указанной области.
2.Найти экстремум функции
 (x 1 , x 2 )  2 x 12  3 x 22  x 1 x 2  2 x 1  x 2 .
Решение
Необходимые условия экстремума:

 4 x1  x2  2  0 ,
x 1

 6 x2  x1  1  0 .
x2
Из системы уравнений
4x1  x 2  2 ,
 x  6 x  1
 1
2
находим x

2
2 
 11
 ( x 1 , x 2 )   ;  .
 23 23 
Достаточные условия экстремума:
 2  2
 2
   2  2  2
,
x 1 x 2
x 1 x 2
 2
 2
 2
 4,
 6,
 1 ,
x 1 x 2
x 12
x 22
   4  6  2  1  8  0 .
2 
 11
;  функция имеет минимум:
 23 23 
Следовательно, в точке 
2
2
11  2 
11  2 
 11 
 2 
( x , x )  2     3     
    2 
  .
23  23 
23  23 
 23 
 23 

1

2
3.Найти условный экстремум функции
 (x 1 , x 2 )  4 x 12  3 x 22  2 x 1 x 2  x 1  x 2
при условии (ограничении)
x1  3 x2  5 .
150
Решение
Составим функцию Лангранжа:
L  4 x 12  3 x 22  2 x 1 x 2  x 1  x 2   ( x 1  3 x 2  5 ) .
Необходимые условия экстремума:
L
 8 x1  2 x2  1    0 ,
x 1
L
 6 x 2  2 x 1  1  3   0 ,
x 2
L
 x1  3 x2  5  0 .

Из системы уравнений
 8 x 1  2 x 2    1 ,
  2 x 1  6 x 2  3   1 ,
 x 1  3 x 2
 5
находим
x 1  1,
x 2  2 ,
 5.
Достаточные условия экстремума:
  2
 2  2
   2  2  2
x 1
x 2
  x 1 x 2
Следовательно, в точке x

2

  8  ( 6 )  2( 2 )  8  6  4  2  0.

 ( x 1 , x 2 )  ( 1;2 ) целевая функция  (x 1 , x 2 )
имеет максимум:
 ( x 1 , x 2 )  4  ( 1 ) 2  3  ( 2 ) 2  2( 1 )( 2 )  ( 1 )  ( 2 ) 
 4  12  4  1  2  13.
▲
1. Найти точку условного экстремума функции
 (x 1 , x 2 , x 3 )  x 1 x 2  x 2 x 3
при ограничениях:
x1  x2  2 .
x  2 x  4
3
 2
2. Мукомольный комбинат реализует муку двумя способами: в розницу через мага-
151
зин и оптом через торговых агентов. При продаже x 1 кг муки через магазин расходы
2
на реализацию составляют x 1 ден. ед., а при продаже x 2 кг муки посредством торго2
вых агентов - x 2 ден. ед.
Определить, сколько килограммов муки следует продавать каждым способом, чтобы затраты на реализацию были минимальными, если в сутки выделяется для продажи
5000 кг муки.
3. Используя метод множителей Лагранжа, найти точку условного экстремума
функции
 (x 1 , x 2 , x 3 )  2 x 1 x 3  x 2 x 3
при ограничениях
x2  2 x3  3 .
x  x  2
 1
2
4. Используя метод множителей Лагранжа, найти точку условного экстремума
функции
 (x 1 , x 2 , x 3 )  x 1 x 2  x 2 x 3
при ограничениях
x1  x 2  2 .
x  x  2
3
 2
5. Используя метод множителей Лагранжа, найти точку условного экстремума
функции
 (x 1 , x 2 , x 3 )  x 1 x 2  x 2 x 3
при ограничениях
x1  x2  2 .
x  x  4
3
 2
6. Используя метод множителей Лагранжа, найти точку условного экстремума
функции
 (x 1 , x 2 , x 3 )  2 x 1  x 2  x 3
при ограничениях
152
x 12  x 22  x 32  1 .
7. Фирма реализует автомобили двумя способами: через розничную и оптовую торговлю. При реализации x 1 автомобилей в розницу расходы на реализацию составляют
4x1  x 12 р., а при продаже x 2 автомобилей оптом - x 22 р.
Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет
200 шт.
8÷17. Дана задача нелинейного программирования
 (x 1 , x 2 )  ax 1 x 2
при ограничениях
a 1 1 x 1  a 1 2 x 2  b1 .
Найти условный экстремум с использованием метода множителей Лагранжа.
Значения коэффициентов целевой функции и системы ограничений
№
варианта
8
9
10
11
12
13
14
15
16
17
a
a11
1
1
2
2
1
3
3
2
-1
-1
-2
1
-3
3
1
1
2
1
-1
3
a1 2
1
3
1
1
3
-2
-1
3
3
-3
b1
1
4
2
3
2
2
3
1
2
2
18. Известен рыночный спрос на определенное изделие в количестве 180 штук. Это
изделие может быть изготовлено двумя предприятиями одного концерна по различным
технологиям. При производстве x 1 изделий первым предприятием его затраты составят 4 x 1  x 1 руб., а при изготовлении x 2 изделий вторым предприятием они состав2
ляют 8 x 2  x 2 руб.
2
Определить, сколько изделий, изготовленных по каждой технологии, может предложить концерн, чтобы общие издержки его производства были минимальны.
19. На двух предприятиях холдинга необходимо изготовить 200 изделий некоторой
153
продукции. Затраты, связанные с производством x 1 изделий на первом предприятии,
2
равны 4 x 1 руб., а затраты, обусловленные изготовлением x 2 изделий на втором
предприятии, составляют 20 x 2  6 x 2 руб.
2
Определить, сколько изделий на каждом из предприятий следует произвести, чтобы
общие затраты на производство необходимой продукции были минимальными.
154
Список литературы
1. Гасс С. Линейное программирование. - М.: Физматгиз, 1961.
2. Гейл Д. Теория линейных экономических моделей. - М.: ИЛ, 1963.
3. Карпилович Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного
программирования. - М.: Физматгиз, 1963.
4. Карлин С. Математические методы в теории игр, программирования и экономике. - М.: "Мир", 1964.
5. Юдин Д.Б., Гольдштейн Б.Г. Линейное программирование. - М.: Физматиздат,
1963.
6. Ашманов С.А. Линейное программирование. - М.: Наука, 1981.
7. Беллман Р. Динамическое программирование: Пер. с англ. - М.: Изд. иностр.
литературы, 1960.
8. Таха Х. Введение в исследование операций: В 2-х книгах/ Пер. с англ. - М.:
Мир, 1985.
9. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование: Учеб. пособие. - 2-е изд., перераб. и доп. - М.: Высш. школа, 1980.
10. Исследование операций в экономике: Учебн. пособие для вузов/ Н.Ш.Кремер,
Б.А.Путко, И.М.Тришин, М.Н.Фридман; Под ред.проф. Н.Ш.Кремера. - М.: Банки и
биржи, ЮНИТИ, 1997.
11. Абчук В.А. Экономико-математические методы: Элементарная математика и
логика. Методы исследования операций. – СПб.: Союз, 1999.
12. Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели
для менеджмента. – СПб.: Издательство «Лань», 2000.
13. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. – 3-е изд., испр. – М.: Дело, 2002.
155
Содержание
Предисловие
1. Линейное программирование
1.1. Задача линейного программирования
1.1.1. Задача об ассортименте продукции
1.1.2. Задача составления смеси (о диете)
1.1.3. Задача о раскрое
1.1.4. Задача о сменно-суточном планировании работы
1.2. Области решений задачи линейного программирования
Вопросы для самопроверки
1.3. Графическое решение задачи линейного программирования
Вопросы для самопроверки
Задания для самостоятельной работы
1.4. Анализ оптимального решения на чувствительность к изменениям исходных условий
1.4.1. Улучшение оптимального решения за счет изменения дефицитного
ограничения
1.4.2. Изменение недефицитного ограничения без изменения оптимального
решения
1.4.3. Степень чувствительности оптимального решения к изменениям
дефицитных ограничений
1.4.4. Пределы изменения коэффициентов целевой функции без изменения
оптимального решения
Вопросы для самопроверки
Задания для самостоятельной работы
1.5. Каноническая форма представления области решений
задачи линейного программирования
Вопросы для самопроверки
1.6. Решение задачи линейного программирования
симплексным методом
Задания для самостоятельной работы
1.7. Интерпретация симплексной таблицы при анализе оптимального решения
задачи линейного программирования на чувствительность
1.8. Двойственные задачи линейного программирования
1.8.1. Экономическая интерпретация задачи, двойственной задаче об
использовании ресурсов
1.8.2. Взаимно двойственные задачи линейного программирования и их свойства
Вопросы для самопроверки
Задания для самостоятельной работы
1.9. Транспортная задача
1.10. Решение транспортной задачи
1.10.1. Определение начального решения
1.10.2. Нахождение вводимой в базис переменной
1.10.3. Нахождение выводимой из базиса переменной
2. Целочисленное линейное программирование
2.1. Задачи целочисленного линейного программирования
2.2. Метод ветвей и границ
Вопросы для самопроверки
Задания для самостоятельной работы
2.3. Метод отсечений (Гомори)
Вопросы для самопроверки
Задания для самостоятельной работы
3. Динамическое программирование
3.1. Задача динамического программирования
3.2. Метод решения задач динамического программирования
3.3. Решение задачи линейного программирования методом динамического
программирования
Вопросы для самопроверки
Задания для самостоятельной работы
4. Нелинейное программирование
4.1. Задачи нелинейного программирования
4.2. Решение задачи нелинейного программирования методом множителей
Лагранжа
Вопросы для самопроверки
Задания для самостоятельной работы
Список литературы