Лекции_2семестра 2014
advertisement
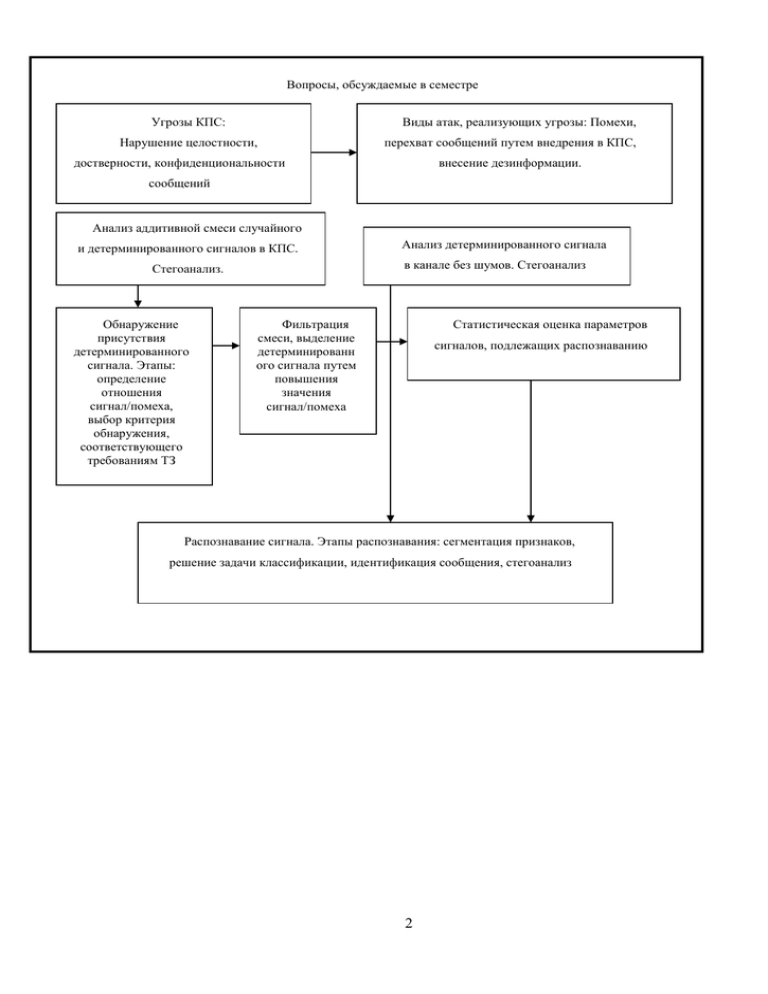
Вопросы, обсуждаемые в семестре
Угрозы КПС:
Виды атак, реализующих угрозы: Помехи,
Нарушение целостности,
перехват сообщений путем внедрения в КПС,
достверности, конфиденциональности
внесение дезинформации.
сообщений
Анализ аддитивной смеси случайного
и детерминированного сигналов в КПС.
в канале без шумов. Стегоанализ
Стегоанализ.
Обнаружение
присутствия
детерминированного
сигнала. Этапы:
определение
отношения
сигнал/помеха,
выбор критерия
обнаружения,
соответствующего
требованиям ТЗ
Анализ детерминированного сигнала
Фильтрация
смеси, выделение
детерминированн
ого сигнала путем
повышения
значения
сигнал/помеха
Статистическая оценка параметров
сигналов, подлежащих распознаванию
Распознавание сигнала. Этапы распознавания: сегментация признаков,
решение задачи классификации, идентификация сообщения, стегоанализ
2
Лекция1. Случайные величины и процессы
1.Вероятность случайного события есть численная мера степени объективной возможности этого
события
и
связана
вероятность
с
опытом,
некоторого события
практическим
понятием
частоты
события,
Тогда
лежит в диапазоне
2. Случайные величины
Событие является качественной характеристикой опыта. Для количественной характеристики
опыта вводится понятие случайной величины, которая в результате опыта может принять то или
иное значение, причем неизвестно заранее, какое именно. Случайные величины возможные значения -
и т.п.
Функция распределения:
величина
и т.п., а
вероятность события
, т.е. вероятность того, что случайная
примет значение, меньшее чем . Интегральный закон распределения
Рассмотрим основные свойства функции распределения.
1.
2.
.
при
имеем
3.
.
4.
.
.Функция
распределения
слева,т.е.
или
непрерывна
.
Плотность распределения вероятности: вероятность попадания случайной величины
полуинтервал
длинной
на
равна приращению функции распределения:
Наз плотностью распределения вероятностей (короче- плотностью вероятности). основные
свойства плотности распределения вероятностей:
1.
В силу монотонного неубывания
2.
Вероятность
и
попадания
случайной
интервал
величины
.
3
на
3
Функция распределения -
Размерность плотности распределения вероятностей
величины
обратна размерности случайной
.
2.1. Система случайных величин
Примером такой системы из двух случайных величин явл. яркости двух источников фона,
расположенных
в
разных
Двумерная функция распределения
неравенств
точках
пространства
.
, т.е. вероятность совместного выполнения двух
и
Свойства двумерной функции распределения выводятся как обобщение, рассмотренных выше
свойств
одномерной
функции
распределения.
Плотность распределения вероятностей системы двух случайных величин представляет собой
вторую смешанную частную производную двумерной функции распределения
Свойства двумерной плотности вероятности
распределения
,так что
аналогичны свойствам одномерного
.
1. Вероятность попадания двумерной случайной величины внутрь элементарного прямоугольника
площадью
.
Тогда вероятность попадания случайной точки
2.
когда закон распределения величины
величина
в произвольную область
не зависит от того, какое значение приняла
.
4
3.
Для независимых непрерывных случайных величин
2.2. Числовые характеристики случайных величин
Математическим ожиданием
называется
называют
-
просто
средним
значением.
1. Основные свойства математического ожидания.
2.
3. Для независимых
4. Математическое ожидание центрированной случайной величины
равно нулю:
Начальный момент -го порядка
говорят о начальном моменте
-го порядка
При этом первые начальные моменты:
представляют
координаты
собой
математические
ожидания
величин
и
и
пределяют
средней точки на плоскости, вокруг которой происходит рассеивание
случайной
точки
Переход к центрированной случайной величине
.
равносилен переносу начала
5
координат
в
среднюю
точку,
координата
которой
равна
математическому
ожиданию.
Центральным моментом -го порядка является
Второй
центральный
носит
название дисперсии.
Основные свойства:
1.
Дисперсия
2.
3.
4.
Дисперсия имеет размерность квадрата случайной величины. Она называется средним
квадратическим отклонением случайной величины
и равна корню квадратному из дисперсии:
2.3. Центральные моменты системы двух случайных величин
Центральным моментом порядка
двумерной случайной величины
называется
На практике широко применяются вторые центральные моменты системы. Два из них
представляют
собой
дисперсии
случайных
Смешанный центральный момент
6
величин
и
:
носит специальное название корреляционного момента (иначе -'момента связи') случайных
величин
.
Безразмерная числовая нормированная характеристика
.
Коэффициент корреляции характеризует наличие некоторой вероятностной зависимости между
величинами.
2.4. Случайные функции
Наглядное представление о случайной функции можно получить из самых различных областей
физики и техники. Осциллограмма напряжения шумов на выходе ПИ, распределение яркости фона в
пространстве, изменение мощности или длины волны ОКГ в процессе генерации, перемещение
броуновской
частицы
-
все
это
примеры
случайных
функций.
Основные определения. Случайная функция -это семейство случайных величин, зависящих от
параметра
,
пробегающего
некоторое
множество
значений
.
В оптике часто аргумент случайной функции является пространственной переменной; такую
функцию
называют случайным
полем.
Примерами случайных полей (случайных функций нескольким переменных - пространственных
координат и времени) могут служить: распределение яркости фона
равномерно освещенного диффузного рассеивателя
;яркость
;высота волн на поверхности
моря
Запись
функцией
наблюдаемой
величины,
т.е.
конкретный
вид,
принимаемый
случайной
называется реализацией(траекторией) случайной функции н обозначается
.
Каждая реализация - это обычная (неслучайная) функция, так что в результате опыта случайная
функция
превращается
в
обычную
2.4.1. Случайная функция как расширение понятия системы случайных величин
7
функцию
.
Случайная величина
вероятностей
полностью задана, если известна ее плотность распределения
,где
случайной
за чертой обозначает, что речь идет о плотности вероятности ординат
функции
Соответствующие
случайные
в
момент
величины
могут
двумерной плотностью вероятности
которых
Случайная
,где
взяты
функция
и
ординаты
задана,
если
ее
вероятностей
выбранных
быть
из
полностью
.
охарактеризованы
указывают моменты времени, для
случайной
конечно-мерная,
известна
значений
времени
для
плотность
любого
области
функции.
распределения
числа
изменения
произвольно
аргумента .
Рассмотренный способ определения случайной функции не всегда удобен вследствие своей
громоздкости. Вместо самих многомерных законов распределения на практике ограничиваются
заданием соответствующих числовых параметров этих законов, подобно тому как в теории
случайных величин часто вместо закона распределения этих величин указывают соответствующим
образом выбранные параметры этих законов.
2.4.2. Моменты случайных функций. Корреляционная теория
Начальный момент первого порядка
является математическим ожиданием ординаты случайной функции в произвольный момент
времени.
Дисперсией случайной
функции
- среднее
называется
квадратическое
неслучайная
отклонение случайной
функция
,
функции.
Для описания внутренней структуры случайного процесса служит второй смешанный центральный
момент (корреляционный момент)
8
Эта
характеристика
называется корреляционной
(иначе
автокорреляционной)
функцией и
выражает степень зависимости между ординатами случайной функции.
Нормированная корреляционная функция
Для определения рассмотренных моментов первого и второго порядков требуется знание только
одномерного и двумерного законов распределения
2.4.3. Стационарные случайные функции
Стационарность - независимость свойств случайной функции от начала
2.4.4. Стационарные процессы
Все вероятностные характеристики стационарного случайного процесса не должны меняться при
изменении
начала
отсчета
времени.
так
что
,
где
- любое число. Тогда для математического ожидания, дисперсии и корреляционной функции
стационарного процесса
получим
Нормальные, или гауссовские, случайные процессы. Плотность распределения вероятностей,
например, в двумерном случае
Для стационарного случайного процесса свойства корреляционной функции приобретают более
простой вид вследствие того, что она является функцией одного аргумента
9
.
характеризует среднюю мощность переменной составляющей,
постоянной составляющей, а
,т.е.
мощность
средняя мощность случайного процесса.
функция четная.
Время кореляции
2.4.5. Однородные поля
В
(где
общем
случае
случайная
функция
,
- любое число), называется однородной по аргументу
удовлетворяющая
условию
.
Еще более частным видом случайной функции двух переменных является однородное изотропное
случайное поле, для которого корреляционная функция
зависит
зависит только от расстояния и не
от
направления
вектора
Понятие радиуса корреляции.
2.4.6. Эргодическое свойство стационарной случайной функции
Чтобы определить основные характеристики стационарной случайной функции, нужно
располагать известным числом реализаций, т.е. иметь ансамбль систем. Однако обычно на практике
имеется одна установка и экспериментатор за данный промежуток времени
может получить
лишь одну реализацию. Оказывается, что эргодичность случайной функции позволяет получать все
статистические
характеристики
из
одной
достаточно
длинной
реализации.
Случайная функции называется эргодической. если любая ее вероятностная характеристика,
полученная усреднением по множеству возможных реализаций с вероятностью сколь угодно
близкой к единице, равна среднему, полученному из одной реализации при достаточно большом
изменении аргумента. В случае эргодического стационарного процесса
математическое
ожидание, дисперсия и корреляционная функция могут быть вычислены по формулам:
10
Для эргодического однородного изотропного случайного поля имеем соответственно
Необходимым условием эргодичности случайных процессов является их стационарность
(однородность).
Случайные процессы, наблюдаемые в стационарно и устойчиво работающих системах, обычно
имеют конечное время корреляции
.
2.4.7. Спектральная плотность стационарной случайной функции
Стационарные случайные функции вследствие неизменности их вероятностных характеристик во
времени имеют квазипериодический характер. Спектральной плотностью случайного процесса
называется прямое преобразование Фурье от корреляционной функции
Внкера):
Справедливо и обратное преобразование Фурье
11
(теорема Хннчииа-
Основные свойства спектральной плотности
является действительной и четной функцией как фурье-образ действительной и четной
функции.
является неотрицательной функцией частоты, так как имеет место следующее
неравенство:
.
Сушествование
конечной
чтобы
дисперсии
в
силу
свойства
требует,
настолько быстро, что
Спектральная плотность
и корреляционная функция Kx(τ) обладают всеми свойствами,
характерными для пары преобразований Фурье.
Случайные функции часто реализуются в технике в виде напряжения или электрического тока.
При
этом
свойства
моменты
второго
выражение
порядка
имеют
энергетический
смысл.
Тогда
пропорционально энергии внутри диапазона частот
с
учетом
, так как
энергия электрического тока пропорциональна квадрату амплитуды соответствующей гармоники.
В случае однородного случайного поля двух переменных
функции
имеет
спектр корреляционной
вид
Обратное преобразование Фурье дает спектральное разложение корреляционной функции
Таким образом, и для однородного случайного поля задание корреляционной функции эквивалентно
12
заданию спектральной плотности и, наоборот, спектральная плотность случайного поля однозначно
характеризует корреляционную функцию.
3. Белый шум
Рассмотрим стационарный случайный процесс
, функция корреляции которого имеет вид
Из
и
времени
следует, что любые две ординаты
некоррелированы.
Про
такой
процесс
в сколь угодно близкие моменты
говорят,
что
он
дельта-коррелирован.
Спектральная плотность дельта-коррелированного процесса
Случайный процесс, спектральная плотность которого постоянна на всех частотах, называется
белым
шумом.
Так
как
дисперсия
становится
бесконечно
большой
то в этом смысле понятно белого шума является математической абстракцией. Однако понятием
белого шума широко пользуются в технике, применяя его в тех случаях, когда энергетическая
ширина спектра случайного процесса много больше, чем полоса пропускания системы, на входе
которой
он
действует.
Рассмотрим приближенную замену реального шума (процесса) на белый шум
систему
корреляции
с
постоянной
времени τc воздействует
реальный
с
,которая характеризуется достаточно широким спектром
следовательно, малым, но конечным временем корреляции
плотности
шум
. Пусть на
функцией
и,
. За значение спектральной
"эквивалентного" белого шума берется значение
Примером шума, который в очень многих случаях можно считать дельта-коррелированным,
является тепловой шум ПИ, обусловленный тепловым движением микрозарядов.
Лекция 2. Преобразование случайных сигналов в КПС.
13
1. Постановка задачи для КПС, как линейной инвариантной системы
H(x)
1.2. Частотный метод расчета
Найдем связь между спектральной плотностью стационарного случайного сигнала на входе и
выходе линейной инвариантной системы. Имеем
Вводя новую переменную
, получим
или
14
Если
- действительная функция (например функция рассеяния некогерентной оптической
системы), то
,так что
В частности, для дисперсии имеем
Для случайного однородного поля W(x,y) соответствующие зависимости имеют вид
Отношение сигнал/помеха (С/П) в КПС
Понятие отношения
широко используют при выделении сигнала из шумов, т.е. речь идёт о
возможности обнаружения или изменения сигнала. Полученные ранее зависимости, описывающие
многомерные преобразования детерминированных и случайных сигналов в КПС, позволяют
определить ОСП на выходе ЭТ. При этом под помехой на выходе понимают смесь внутреннего шума
с внешней (от фоновых излучений) помехой.
Рассмотрим методику определения сигнала и помехи на выходе ЭТ, структурная схема которой
приведена на рис.
ИС
СП
ПФ
СУ
ДИ
ЭТ
Пространственно-временной тракт
Под ОСП в зависимости от специфики задачи принято понимать:
1. отношение квадрата амплитуды сигнала к дисперсии помехи;
2. отношение квадрата пикового значения сигнала к дисперсии результирующей помехи;
3. отношение амплитуды сигнала к среднеквадратическому значению помехи;
4. отношение мощности сигнала к мощности случайной помехи;
15
5. отношение энергии сигнала к энергии случайной помехи.
Указанные ОСП связаны со статистическими характеристиками обнаружения
В предметной плоскости на ПФ расстоянии l от ЛОЭС расположен излучающий объект Обт с
энергетической яркостью
, и во входной зрачок ОС попадает поток излучения от объекта и
случайного фона. Далее суммарное поле освещённости преобразуется СУ и ДИ во временной
электрический сигнал, который затем обрабатывается в ЛЭС. Считаем, что яркостное поле
случайного фона является однородным и описывается пространственным спектром
корреляционной функцией
, приведёнными к плоскости анализа. Пусть ЧВС сигнала от
излучающего объекта на выходе ЭТ описывается функцией
помехи
или
, а спектр мощности фоновой
. Кроме этого, на выходе ЭТ будет присутствовать помеха, обусловленная шумами
ДИ и ЭТ, спектр мощности которой описывается зависимостью
.
Обычно счтают, что помеха от внешнего фона и внутренние шумы некоррелированы между
собой, поэтому при расчёте их спектральные плотности можно складывать. Спектр мощности
результирующей помехи на выходе ЭТ при апериодическом сканировании определяется формулой
Рассмотрим функциональную схему ЭПС обнаружения, изображенную на рис. 1.
16
Рис. 1.Функциональная схема обнаружения с предварительной фильтрацией сигнала: СПО-система
первичной обработки сигнала; ФЛ-бесшумный линейный ЧВФ; ПУ-пороговое устройство.
Аддитивная смесь полезного сигнала и фоновой помехи, приходящая на вход системы первичной
обработки и (СПО), преобразуется этой системой в некоторую одномерную реализацию
,
являющуюся функцией времени и представляющую собой электрический сигнал, снимаемый с ДИ. В
силу линейности СПОИ реализация
помехи
(рис.1) состоит из суммы полезного сигнала
и
, которая учитывает как фоновую помеху, так и собственный шум ПИ. Вид реализации
также изображен на рис. 1, где штриховой кривой показан полезный сигнал, пиковое значение
которого соответствует времени
время
Реализация
. Поскольку момент появления цели в плоскости неизвестен, то
является
случайной
величиной.
поступает на вход нешумящего линейного ЧВФ, имеющего ПФ
которого формируется реализация
, на выходе
. ПУ выдает решение по методу
однократного отсчета, непрерывно сравнивая мгновенное значение реализации
с порогом,
рассчитанным в соответствии с одним из критериев качества. Надо только установить значения
необходимых для расчета параметров полезного сигнала и помехи на входе ПУ с учетом
17
характеристик
Обозначив
ЧВС
через
и
выходе
ЧВФ.
полезного
сигнала
и
энергетический
ЧВС,
помехи
на
входе
ЧВФ
, а аналогичные ЧВС, корреляционную функцию и дисперсию помехи на
ЧВФ
–
через
Сигнал запаздывает по отношению к началу реализации на время
,
и
,
.
. Поэтому ЧВС сигнала на входе
ЧВФ
,
где
- ЧВС полезного сигнала для которого за начало отсчета времени принято
Для ЧВС
на выходе получим
Для полезного сигнала, корреляционной функции и дисперсии помехи на выходе ЧВФ имеем
2. Оценка мгновенного значения ОСП на выходе ЧВФ
Найдем функцию
мгновенного значения ОСП от времени. Из
, которую можно рассматривать как зависимость
и
получим
18
Используя неравенство Шварца-Буняковского
где
и
- произвольные комплексные функции временной частоты
и, полагая в нем
получим
Откуда в соответствии с
имеем
.
В итоге можно сделать важный вывод: ОСП на выходе линейного ЧВФ в произвольный момент
времени не может быть больше величины
19
В
формуле
функции
ЧВФ.
и
(5.64)
для
простоты
опущен
подстрочный
индекс
у
,
так
что
определяют ЧВС полезного сигнала и энергетический ЧВС помехи на входе
Лекция 2. Стеганография и стегоанализ
20
21
Физиология зрения человека
Цветовое зрение
В глазу человека содержатся два типа светочувствительных клеток (рецепторов): высоко
чувствительные палочки,
отвечающие
за
сумеречное
чувствительные колбочки, отвечающие за цветное зрение.
Видимый солнечный спектр
22
(ночное)
зрение,
и
менее
Нормализованные графики светочувствительности колбочек человеческого глаза S, M, L.
Пунктиром показана сумеречная, «чёрно-белая» восприимчивость палочек В сетчатке глаза человека
есть
три
вида
колбочек,
максимумы
на красный, зелёный и синий участки
чувствительности
которых
приходятся
спектра. Равномерное раздражение всех трёх элементов,
соответствующее средневзвешенному дневному свету, также вызывает ощущение белого цвета
Физиология слуха человека
1.
Пороги слухового ощущения.
Чувствительность слухового анализатора к звукам различной высоты неодинакова.
Человеческое ухо наиболее чувствительно к звукам с частотой колебаний от 1000 до 3000, по мере
же понижения и повышения частоты колебаний чувствительность падает. Особенно резкое падение
чувствительности отмечается в области самых низких и самыхвысокихзвуков.
Минимальная сила
звука, способная вызвать
ощущение едва слышимого звука, называется порогом слухового ощущения.
Чем меньше величина звуковой энергии, необходимая для получения ощущения едва слышимого
звука, т. е. чем ниже порог слухового ощущения, тем выше чувствительность уха к данному звуку.
В области средних частот (от 1000 до 3000 гц) пороги слухового восприятия оказываются
наиболее низкими, а в области низких и высоких частот пороги повышаются.
При нормальном слухе величина порога слухового ощущения равна 0 дб.
Нуль децибел означает не отсутствие звука (не «нуль звука»), а нулевой уровень, т. е. уровень
отсчета при измерении интенсивности воспринимаемых звуков, и соответствует пороговой
интенсивности при нормальном слухе.
Нулевым уровнем силы звука принято считать величину давления,
соответствующего порогу слухового ощущения при нормальном слухе для тона в 1000 гц.
При увеличении силы звука ощущение громкости звука усиливается, но при достижении силы
звука определенной величины нарастание громкости прекращается и появляется ощущение давления
или даже боли в ухе. Сила звука, при которой появляется ощущение давления или боли, называется
порогом неприятного ощущения или порогом дискомфорта.
Расстояние между порогом
слухового ощущения и порогом дискомфорта оказывается наибольшим в области средних частот
(1000—3000 гц) и достигает здесь 130 дб.
23
Область слухового восприятия у нормально слышащего человека ограничена по частоте и по силе
звука. По частоте эта область охватывает диапазон от 16 до 20000 гц (частотный диапазон слуха), а
по силе — 130 дб (динамический диапазон слуха).
Принято считать, что область речи, т. е. частотный и динамический диапазон, необходимый для
восприятия звуков речи, занимает лишь небольшую часть всей области слухового восприятия, а
именно по частоте от 500 до 3000 гц и по силе от 50 до 90 дб над порогом слышимости. Такое
ограничение области речи по частоте и интенсивности может быть принято лишь весьма условно,
так как оно оказывается действительным только в отношении наиболее важной для понимания речи
области воспринимаемых звуков, но далеко не охватывает всех звуков, входящих в состав речи.
(Стандарт GSM)
Целый ряд звуков речи, как например согласные [с], [з], [ц], содержит форманты, лежащие
значительно выше 3000 гц, а именно до 8600 гц. Что касается динамического диапазона, то нужно
учитывать, что уровень интенсивности тихого шепота равен 10—15 дб и что даже в громкой речи
имеются такие составные элементы, интенсивность которых не превышает уровня обычной
шепотной речи, т. е. 25 дб; к числу таких элементов относятся, например, некоторые глухие
согласные. Следовательно, для полноценного различения на слух всех звуков речи необходима
сохранность всей или почти всей области слухового восприятия, как в отношении частоты, так и в
отношении интенсивности звука.
24
Г
G
ц
SM
Рис.
3.
Область
слухового
восприятия.
На рисунке 3 представлена область звуков, воспринимаемых нормальным ухом человека.
Верхняя кривая изображает порог слышимости звуков различной частоты, нижняя кривая — порог
неприятного ощущения. Между этими кривыми располагается область слухового восприятия,
т. е.
весь диапазон слышимых человеком звуков. Заштрихованные части диаграммы обозначают область
наиболее часто встречающихся звуков музыки и речи. .
2.
Слуховая адаптация (Маскирование)и слуховое утомление. Звуковая травма.
При воздействии звуковых раздражений происходит временное понижение чувствительности
органа слуха. Так, например, выйдя на шумную улицу, человек, обладающий нормальным слухом,
25
ощущает шум улицы как очень громкий, соответственно его действительной интенсивности. Однако
через некоторое время уличный шум ощущается уже как значительно менее громкий, хотя
фактически интенсивность шума не изменяется. Это снижение ощущения громкости является
следствием понижения чувствительности слухового анализатора в результате воздействия сильного
звукового раздражителя. После прекращения воздействия шума, когда, например, человек входит с
шумной улицы в тихое помещение, чувствительность слухового органа быстро восстанавливается, и,
выйдя вновь на улицу, человек опять будет ощущать уличный шум как очень громкий. Такое
временное снижение чувствительности получило название адаптации (от лат. adaptare —
приспособлять).
Адаптация
является
защитно-приспособительной
реакцией
организма,
предохраняющей нервные элементы слухового анализатора от истощения под воздействием
сильного раздражителя.
Изменение чувствительности в процессе адаптации происходит как
в периферическом, так и в центральном конце слухового анализатора. При воздействии звука на
одно
ухо
чувствительность
изменяется
в
обоих
ушах.
3. Маскировка звука.
Если какой-либо звук воспринимается на фоне действия другого звука,
то первый звук ощущается менее громким, чем в тишине; он как бы
заглушается другим звуком.
Это явление носит название
маскировки звука. Для звуков разной высоты маскировка выражена
неодинаково. Высокие звуки сильно маскируются низкими и, наоборот,
сами оказывают очень небольшое маскирующее действие на низкие звуки. Наиболее сильно выражено маск
высоте к маскируемому звуку.
На практике приходится часто иметь дело с маскирующим действием
различных шумов.
Так, например, шум городской улицы оказывает заглушающее (маскирующее)
действие, достигающее днем 50—60 дб.
- знакомство с характерными рыночными продуктами:
Blindside, DataMark, Technologies, Digital Picture Envelope, gifshuffle, Hide4PGP, Hide4PGP,
Hide4PGP, Invisible Secrets, JPHIDE and JPSEEK, MP3Stego, NICETEXT, OutGuess, Scramdisk, Snow,
SteganoGifPaletteOrder, Steganos, Stego, StegParty, TextHide, wbStego.
- знакомство с характерной частью основных современных методов:
Алгоритм Катера (Kutter).
Алгоритм Брундокса (Bruyndonckx)
Алгоритм Ленгелаара (Langelaar)
26
Алгоритм Питаса (Pitas)
Алгоритм Роджена (Rongen)
Алгоритм PatchWork
Алгоритм Бендера (Bender)
Алгоритм LSB
Алгоритм Коча (Koch)
Алгоритм Бенхама (Benham)
Алгоритм Подилчука (Podilchuk)
Алгоритм Хсю (Hsu)
Алгоритм Кокса (Cox)
Алгоритм Барни (Barni)
Алгоритм Чайа (Chae)
Подробно вопросы стеганографии и стегоанализа рассмотрены в отдельном пособии.
27
Лекция 4
4.1 Волновая теория
Связь магнитного и электрического поля
• Электрический ток создаёт магнитную индукцию
B=μ
(закон Ампера)
I/2πr
• Переменный поток магнитного поля создаёт
электрическое поле (закон Фарадея)
4. 3
28
I=
dф/dt
Второе уравнение Максвелла
•
В основной статье Максвелл впервые сформулировал понятие
электромагнитного поля как физической реальности, имеющей собственную
энергию и конечное время распространения, определяющее запаздывающий
характер электромагнитного взаимодействия.
Не только ток, но и изменяющееся со временем электрическое поле (ток
смещения) порождает магнитное поле. В свою очередь, в силу закон
Фарадея, изменяющееся магнитное поле снова порождает электрическое.
Второе уравнение Максвелла выражает закон электромагнитной индукции
Фарадея: ЭДС в любом замкнутом контуре равна скорости изменения (т. е.
производной по времени) магнитного потока.
•
•
Итак, получаем: rotE = - dB/dt.
В результате, в пустом пространстве может распространяться электромагнитная волна.
Из уравнений Максвелла следовало, что её скорость равна скорости свет,
поэтому Максвелл сделал вывод об электромагнитной природе света.
4.4
Третье и четвертое уравнения
Максвелла
•
Они основаны на теореме Гаусса, утверждающей, что поток вектора электрической
индукции через любую замкнутую поверхность равен заряду внутри этой поверхности.
•
Третье уравнение Максвелла: div D = р.
•
Четвертое уравнение утверждает, что магнитных зарядов в природе не существует,
поэтому:div B = 0.
Распространение электромагнитных волн со скоростю света первоначально
интерпретировалось как возмущения некоторой среды, так называемого эфира.
Классическая электродинамика, основанная на уравнениях Максвелла, лежит в основе
многочисленных приложений электро- и радиотехники, СВЧ и оптики. До настоящего
времени не было обнаружено ни одного эффекта, который потребовал бы
видоизменения уравнений.
29
4.5
Дифференциальная форма уравнений
Максвелла
•
Уравнения Максвелла представляют собой систему из восьми (два
векторных с тремя компонентами каждое и два скалярных)
линейных дифференциальных уравнений в частных производных
1-го порядка для 12 компонент четырёх векторных функций ( D,E,H,B):
30
4.6
Интегральная форма уравнений
Максвелла
31
4.7
Уравнения Максвелла в среде
•
Чтобы получить полную систему уравнений электродинамикик системе уравнений
Максвелла необходимо добавить материальные уравнения, связывающие
величины j, H , D , E , B, в которых учтены индивидуальные свойства среды. Способ
получения материальных уравнений дают молекулярные
теории поляризации, намаг и электропроводиченностиности среды, использующие
идеализированные модели среды. Применяя к ним уравнения
классической или квантовой механики, а также методы статистической физики, можно
установить связь между векторами j, H , D с одной стороны и E, B с другой стороны.
Связанные заряды и токи
32
4.8
Материальные уравнения
•
Материальные уравнения устанавливают связь между D, H и E, B . При этом
учитываются индивидуальные свойства среды. На практике в материальных уравнениях
обычно используются экспериментально определяемые коэффициенты (зависящие в
общем случае от частоты электромагнитного поля), которые собраны в различных
справочниках физических величин.
В слабых электромагнитных полях, сравнительно медленно меняющихся в
пространстве и во времени, в случае изотропных, неферромагнитных и не
сегнетоэлектрических сред справедливо приближение, в котором
поляризуемость и намагниченность линейно зависят от приложенных полей:
33
4.9
Продолжение…
В проводниках существует связь между плотностью тока и напряжённостью
электрического поля, выражаемая законом Ома:
В анизотропной среде связь между напряжённостями полей и индукциями имеют
различные коэффициенты по каждой координате.
4.10
34
Продолжение…
Хотя для широкого класса веществ линейное приближение для слабых полей
выполняется с хорошей точностью, в общем случае зависимость между
D, H и E, B может быть нелинейной. В этом случае проницаемости среды не
являются константами, а зависят от величины поля в данной точке. Кроме того, более
сложная связь между D, H и E, B наблюдается в средах с пространственной или
временной дисперсиями. В случае пространственной дисперсии токи и заряды в
данной точке пространства зависят от величины поля не только в той же точке, но и в
соседних точках. В случае временной дисперсии поляризация и намагниченность
среды не определяются только величиной поля в данный момент времени, а зависят
также от величины полей в предшествующие моменты времени. В самом общем
случае нелинейных и неоднородных сред с дисперсией, материальные уравнения в
системе СИ принимают интегральный вид:
4.11
Уравнения в изотропных и однородных
средах без дисперсии
• В изотропных и однородных средах без дисперсии уравнения
Максвелла принимают следующий вид:
35
4.12
Граничные условия
•
Во многих случаях неоднородную среду можно представить в виде совокупности
кусочно-непрерывных однородных областей, разделённых бесконечно тонкими
границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая»
на границах получающиеся решения. В частности, при рассмотрении решения в
конечном объёме необходимо учитывать условия на границах объёма с окружающим
бесконечным пространством. Граничные условия получаются из уравнений Максвелла
предельным переходом. Для этого проще всего воспользоваться уравнениями
Максвелла в интегральной форме.
Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной
рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно
получить следующую связь между компонентами поля в двух областях, примыкающих к
границе:
36
4. 13
Продолжение…
Эти граничные условия показывают непрерывность нормальной компоненты
вектора магнитной индукции (нормальная компонента электрической индукции
непрерывна только при отсутствии на границе поверхностных зарядов).
37
4.14
Волновое уравнение
•
Уравнения Максвелла являются дифференциальными уравнениями первого
порядка по координатам и времени. Однако, во второй паре в каждое
уравнение входят обе неизвестные векторные функции E и B. При отсутствии
зарядов и токов можно перейти к уравнениям второго порядка, каждое из
которых зависит только от одного, электрического или магнитного поля:
Такие уравнения называются волновыми.
38
4.15
Уравнение Гельмгольца
•
При отсутствии электрических зарядов в среде, уравнение
Гельмгольца принимает вид:
где
39
4. 16
Плоские электромагнитные волны
•
Предположим, что напряжённость электрического поля и магнитная
индукция являются произвольными функциями следующей комбинации
координат и времени:
где n — некоторый постоянный вектор. В этом случае E и B удовлетворяют
уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует
следующая связь:
40
4.17
Вывод решения для плоской волны
4.18
Продолжение…
• Вектор Пойнтинга (плотность потока энергии), независимо от системы
единиц, связан с полной плотностью энергии следующим образом:
Это соотношение соответствует уравнению связи импульса и энергии для
безмассовой частицы в релятивистской теории. Однако, скорость
в среде меньше чем скорость света в вакууме .
41
4. 19
Продолжение…
•
Важный частный случай решения в виде плоских волн возникает, когда напряжённости
полей являются гармоническими периодическими функциями. Выберем координатную
ось Z вдоль волнового вектора k. Тогда вектор электрического поля (как, впрочем, и
магнитного) будет лежать в плоскости
то есть
. Если по каждой проекции в этой плоскости электрическое поле
совершает периодические колебания, то такую волну называют монохроматической
плоской волной:
Сравнение с общим решением для плоской волны, приводит к следующей связи между
вектором k и константой , которое называется уравнением дисперсии:
В этом случае, вектор k называется волновым вектором, а — круговой
частотой монохроматической электромагнитной волны. Модуль волнового вектора и
круговая частота связаны с длиной волны и её частотой следующим образом:
42
4.20
Численное решение уравнений Максвелла
•
•
Основными методами являются проекционные, в которых решение проецируется на
какой-либо удобный функциональный базис, и дискретизационные — область
пространства разбивается на множество малых конечных областей.
Для компьютерных расчетов чаще применяются более универсальные
дискретизационные методы:
Метод конечных элементов (FEM), который используется для решения широкого
класса задач, сводящихся к уравнениям в частных производных. В методе конечных
элементов рассматриваемая область пространства, в которой ищется решение,
разбивается на большое число простых дискретных элементов, обычно, но не
обязательно, треугольной (в двумерном случае) или тетраэдральной формы (в
трёхмерном случае). Форма и плотность элементов адаптируются к требованиям
задачи. Поведение отдельных элементов рассматривается как результат линейного
взаимодействия соседних узлов решётки разбиения под действием внешних сил и
описывается матричными уравнениями. Решение задачи сводится, таким образом, к
решению разреженных систем большого числа линейных матричных уравнений.
Метод конечных разностей во временной области (FDTD) для нахождения временных
и спектральных зависимостей был разработан специально для решения уравнений
Максвелла, в которых изменение электрического и магнитного поля во времени
зависит от изменения, соответственно, магнитного и электрического поля в
пространстве. В рамках этого метода область пространства и временной интервал
подвергаются равномерной дискретизации с заданием начальных условий.
Полученные из уравнений Максвелла конечно-разностные уравнения решаются в
каждый последующий момент временной сетки, пока не будет получено решение
поставленной задачи на всем требуемом временном интервале.
43
4.21
Продолжение…
•
•
•
•
•
Идея метода конечных разностей (метода сеток) известна давно, с
соответствующих трудов Эйлера. Однако практическое применение этого
метода было тогда весьма ограничено из-за огромного объема ручных
вычислений, связанных с размерностью получаемых систем алгебраических
уравнений, на решение которых требовались годы. В настоящее время, с
появлением быстродействующих компьютеров, ситуация в корне изменилась.
Этот метод стал удобен для практического использования и является одним
из наиболее эффективных при решении различных задач математической
физики.
Основная идея метода конечных разностей (метода сеток) для
приближенного численного решения краевой задачи для двумерного
дифференциального уравнения в частных производных состоит в том, что
1) на плоскости в области А, в которой ищется решение, строится сеточная
область Аs (рис.1), состоящая из одинаковых ячеек размером s ( s – шаг
сетки) и являющаяся приближением данной области А;
2) заданное дифференциальное уравнение в частных производных
заменяется в узлах сетки Аs соответствующим конечно-разностным
уравнением;
3) с учетом граничных условий устанавливаются значения искомого решения
в граничных узлах области Аs .
4.22
44
Продолжение…
Решая полученную систему конечно-разностных алгебраических уравнений,
получим значения искомой функции в узлах сетки Аs , т.е. приближенное
численное решение краевой задачи. Выбор сеточной области Аs зависит от
конкретной задачи, но всегда надо стремиться к тому, чтобы контур сеточной
области Аs наилучшим образом аппроксимировал контур области А.
Рассмотрим простейший и наглядный случай (уравнение Лапласа)
(1)
Где p ( x, y ) – искомая функция, x, y –
прямоугольные координаты плоской области и получим
соответствующее ему конечно-разностное уравнение.
45
4. 23
Продолжение…
Заменим частные производные
разностными отношениями:
и
в уравнении (1) конечно-
Тогда решая уравнение (1) относительно p ( x, y ), получим:
(2)
• Задав значения функции p ( x, y ) в граничных узлах контура сеточной
области Аs в соответствии с граничными условиями и решая
полученную систему уравнений (2) для каждого узла сетки, получим
численное решение нашей краевой задачи (1) в заданной областиА.
• Число уравнений вида (2) равно количеству узлов сеточной
области Аs, и чем больше узлов, т.е. чем мельче сетка, тем меньше
погрешность вычислений. Однако с уменьшением шага s возрастает
размерность системы уравнений и следовательно, время решения.
Принцип Гюйгенса — Френеля формулируется следующим образом:
Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения,
порождающего вторичные сферические волны, а результирующее световое поле в каждой точке
пространства будет определяться интерференцией этих волн.
Густав Кирхгоф придал принципу Гюйгенса — Френеля строгий математический вид, показав,
что его можно считать приближенной формой теоремы, называемойинтегральной теоремой
Кирхгофа (см. метод Кирхгофа).
46
Фронтом волны точечного источника в однородном изотропном пространстве является сфера.
Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от
точечного источника, одинакова.
Дальнейшим обобщением и развитием принципа Гюйгенса — Френеля является формулировка
через интегралы по траекториям, служащая основой современной квантовой механики.
Рефракция волн по Гюйгенсу
Дифракция волн по Гюйгенсу
Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и
объясняющий механизм распространения волн, в частности, световых.
Описание
Принцип
Гюйгенса —
Френеля
является
развитием
принципа,
который
ввёл Христиан
Гюйгенс в 1678 году: каждая точка поверхности, достигнутая световой волной, является вторичным
источником световых волн. Огибающая вторичных волн становится фронтом волны в следующий
47
момент времени. Принцип Гюйгенса объясняет распространение волн, согласующееся с
законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан
Френель в 1815
году дополнил
принцип
Гюйгенса,
введя
представления
о когерентности и интерференции элементарных волн, что позволило рассматривать на основе
принципа Гюйгенса — Френеля и дифракционные явления.
Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения,
порождающего вторичные сферические волны, а результирующее световое поле в каждой точке
пространства будет определяться интерференцией этих волн.
Густав Кирхгоф придал принципу Гюйгенса — Френеля строгий математический вид, показав,
что его можно считать приближенной формой теоремы, называемойинтегральной теоремой
Кирхгофа (см. метод Кирхгофа).
Фронтом волны точечного источника в однородном изотропном пространстве является сфера.
Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от
точечного источника, одинакова.
Дальнейшим обобщением и развитием принципа Гюйгенса — Френеля является формулировка
через интегралы по траекториям, служащая основой современной квантовой механики.
Для справки: ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ПОЛЯ
Градиент скалярного поля:
,
Определен, как вектор в напавлении скорейшего роста U:
Производная скалярного поля U по направлению l :
Для непрерывных функций (P, Q, R) с непрерывными частными производными 1 порядка:
48
Определен поток векторного поля:
через поверхность S (поверхностный интеграл):
Дивергенция векторного поля F(P, Q, R)
div F – скаляр.
Если:
то точка M0 - источник. Соответсвеннно, точка M0 - сток, если:
Если div F = 0, векторное поле – соленоидальное. Поток соленоидального поля через любую
поверхность равен 0.
Линейный интеграл по ориентированной кривой K:
является криволинейным (работа вдоль К).
По замкнутому контуру C линейный интеграл принимает вид:
49
и называется циркуляцией векторного поля вдоль контура С.
Вихрь (ротор) векторного поля F(P, Q, R).
Если rot F = 0 для всех точек поля, поле безвихревое (потенциальное).
Формула Стокса.
С – замкнутый контур, ограничиваюший поверхность S c
Z
направляющими косинусами:
γ
S
Вектор нормали к S
β
Направление
обхода
α
X
Y
Формула Стокса в векторной форме.
50
Циркуляция вектора вдоль замкнутого контура С, ограничивающего поверхность S, равна потоку
вихря через эту поверхность:
Формула Остроградского – Гаусса.
Если Т – замкнутая область, ограниченная гладкой поверхностью S,
то:
Формула Остроградского – Гаусса в векторной форме.
- интеграл от дивергенции векторного поля F, распространенный по обьему Т равен потоку
вектора через поверхность S, ограничивающую объем Т.
Формула Грина.
С – граница области D. P(X, Y), Q(X, Y) – непрерывны в замкнутой области D,
Тогда:
51
.
Лекция 5
1. Элементы скалярной теории дифракции
Основы электромагнитной теории, базирующейся на уравнениях Максвелла, были в
основном сформулированы еще в XIX веке. В теории ставится задача описать
электромагнитное поле с помощью механических моделей. В теории принято, что при
наличии электрических зарядов и токов в пространстве устанавливается возбужденное
состояние, которое называют электромагнитным полем. При этом считается, что
колебания электрических зарядов в виде ограниченных движений в окрестности
некоторого среднего положения, обладающие той или иной степенью повторяемости,
приводят к соответствующим изменениям состояния пространства. Электромагнитное
поле рассматривается, как частный случай волнового поля. Это физическое поле,
существующее
в
форме
волн
и
описываемое
с
помощью
совокупности
пространственно-временных распределений физических величин, характеризующих
рассматриваемые волны.
По
Максвеллу электромагнитные
физического
состояния
среды
волны представляют
(возмущения),
собой
обусловленные
изменения
колебаниями
электрических зарядов в этой среде, распространяющиеся со скоростью света и
несущие
с
собой
электрического поля
энергию.
Их
характеризуют
и магнитной индукции
52
векторами
напряженности
. Вид волн определяется в
результате решения волнового уравнения, описывающего их распространение в
пространстве, которое в свою очередь получается из уравнений Максвелла .
В рамках скалярной теории дифракции в любой точке
однородной среды
в областях, свободных от токов и зарядов (в частности, отсутствуют источники
излучения), вещественная функция
, которая описывает электромагнитное
возмущение, удовлетворяет скалярному однородному волновому уравнению
где
– оператор Лапласа;
– скорость света в среде;
км/с – скорость света в вакууме;
– показатель преломления.
В скалярной теории дифракции
представляет собой одну из двух взаимно
перпендикулярных декартовых компонент
и
электрического поля,
колеблющихся в плоскости, перпендикулярной направлению распространения волны.
Скалярная теория не позволяет учесть явление поляризации и тонкие эффекты
дифракции. Однако для инженерных приложений, в частности при модельном
представлении реальных КПС такое допущение дает удовлетворительные результаты.
Но даже при описанных допущениях решить волновое уравнение удается для
небольшого числа частных случаев. Одним из таких решений является модель,
которая строится на представлении суперпозиции плоских и сферических волн. Такая
модель с достаточной адекватностью позволяет описывать преобразование сигналов в
ультрафиолетовом, оптическом и инфракрасном диапазонах. В некоторых диапазонах
электромагнитного излучения, используемых радиоэлектронными системами (РЭС),
входящими в состав КПС, ограничения скалярной теории дифракции недопустимы.
53
Границы
ее
применимости
рассматриваются
на
основе
соответствующих
классификаций.
РЭС могут работать в диапазоне от 3 кГц до 300 ГГц. Несущая частота сигнала,
передающего (несущего) сообщение, существенно влияет на распространение,
отражение и рассеяние радиоволн. Поэтому весь радиодиапазон частот условно
разделен на участки, каждый из которых имеет свои особенности, в частности способ
модельного представления (табл. 1.5).
Таблица 1.5.
Диапазон
Длина Название
радиочастот
волны радиочастот
3...30 кГц
10...100
км
диапазона
Название
диапазона
радиоволн
Сверхнизкие частоты (СНЧ)Мириаметровые волны
30...300 кГц
1...10 кмНизкие частоты
Километровые волны
0.3...3 МГц
100...1000
Средние частоты
Гектометровые волны
3...30 МГц
10...100 Высокие
м
частоты
Декаметровые волны
30...300 МГц
Очень
1...10 м
(ОВЧ)
м
высокие
Ультравысокие
300...3000 МГц 0,1...1 м
(УВЧ)
частоты
Метровые волны
частоты
Дециметровые волны
3...30 ГГц
1...10 смСверхвысокие частоты (СВЧ)
Сантиметровые волны
30...300 ГГц
Крайне
0,1...10 см
(КВЧ)
высокие
частоты
Миллиметровые волны
Дециметровые волны распространяются только в пределах прямой видимости,
54
интенсивно отражаются от объектов, благодаря наличию совершенной элементной
базы в соответствующих РЭС достигается направленность излучения и приема.
Сантиметровые волны также распространяются только в пределах прямой
видимости,
интенсивно
отражаются
от
различных
объектов,
что
позволяет
организовывать защищенные КПС даже в условиях возникновения ретроотражений в
замкнутых пространствах. Возможно достижение высокой направленности излучения
и приема. Элементная база позволяет реализовать КПС с псевдослучайным
сканированием несущей и псевдослучайным распределением поднесущих частот.
Миллиметровые волны
поглощаются
в
атмосфере
в
самой
высокой
степени.направленности. РЭС, реализующие соответствующие КПС, обладают
высокой направленностью излучения и приема.
Как показывает анализ, наиболее часто в РЭС применяются диапазоны ОВЧ, УВЧ и
СВЧ. Излучение в этих диапазонах частот интенсивно отражаются от объектов,
антенны компактны и обеспечивают высокую направленность излучения и приема.
Анализ РЭС связи показывает перспективность применения этих диапазонов. Для этих
диапазонов наиболее активно развивается элементная база РЭС. Если в КПС с РЭС не
используется
эффект
поляризации
и
вполняются
рассматриваемая модель приемлема.
55
описанные
ниже
условия
Рис.1. Зоны свободного пространства, где наблюдается дифракция Зоммерфельда,
Френеля и Фраунгофера
Рис.2. Зоны пространства за фокусирующим элементом (объектив ОС, антенна
РЛС), где наблюдается дифракция Френеля и Фраунгофера
Радиотехнические
системы
извлечения
информации
в
зависимости
от
информационного параметра подразделяют на амплитудные, фазовые и частотные. К
56
первым относятся, например, системы определения направления прихода радиоволн с
помощью направленных антенн; ко вторым — фазовые радионавигационные системы;
к третьим — доплеровские системы измерения радиальной скорости.
В радиотехнических системах передачи информации сигналы формируются путем
изменения
тех
или
иных
параметров переносчика
информации
по
закону
передаваемых сообщений. Процесс изменения параметров переносчика информации
принято называть модуляцией, если передаваемые сообщения непрерывные, и
манипуляцией,
если
передаваемые
сообщения
цифровые.
В
случае,
когда
переносчиком является гармоническое колебание, модулирующими параметрами
могут быть его амплитуда, частота и фаза. Различают непрерывные РТС передачи
информации с амплитудной (AM), частотной (ЧМ) и фазовой (ФМ) модуляциями.
В импульсных РТС передачи информации модулируемыми параметрами могут
являться амплитуда импульса, длительность, частота следования и фаза (положение
относительно точки отсчета), число импульсов, а также комбинация импульсов и пауз,
определяющих код. Соответственно, различают РТС передачи информации с
амплитудно-импульсной (АИМ), широтно-импульсной (ШИМ), частотно-импульсной
(ЧИМ), фазоимпульсной (ФИМ), импульсно-кодовой (ИКМ) модуляциями. Возможны
и другие виды систем.
В цифровых РТС передачи информации применяются относительная фазовая
(ОФМ), частотная (ЧМ), амплитудная (AM) манипуляции и другие более сложные
виды.
Приведенная классификация позволяет выявить особенности РЭС и учесть их при
проектировании методов и средств защиты. Границы применимости рассматриваемой
модели распространения электромагнитного излучения для РЭС определяются
нижеописанными условиями.
1.1. Скалярные монохроматические волны
В волновой теории элементарным сигналом считают монохроматическую волну,
распространяющуюся
в
пространстве
и
во
57
времени.
Если
ее
временная
частота
лежит
приблизительно
в
(соответственно длина волны в вакууме
интервале
от
до
Гц
изменяется от 0,75 мкмдо 0,4 мкм), то речь
идет об оптическом диапазоне. Если длина волны в вакууме
изменяется от
0,75 мкм до 30 мкм, то такой диапазон называется инфракрасным. Для радиодиапазона
длина волны изменяется от долей мм до десятков километров. Решение волнового
уравнения (1), определяющее вид монохроматической волны в точке
в
момент времени , можно представить в виде скалярной функции
Величину
,
большую
косинуса
нуля,
– полной
времени
так
Величину
называют амплитудой,
фазой,
и
от
зависящей
пространственных
называют временной,
а
аргумент
как
от
координат
илициклической,
.
частотой
оптического излучения (представляет число колебаний в секунду, Гц), которая по
порядку величины равна
Гц, а величину
Последняя определяет число колебаний в
– угловой частотой.
секунд. При замене на
значение
функции остается неизменным, поэтому является временным периодом колебаний.
Волновую функцию в форме (4) называют временным гармоническим оптическим
сигналом.
Она
определяет
поляризованной волны
монохроматическую
волну.
В
случае
линейно
характеризует напряженность электрического или
магнитного поля как физическую величину.
Расчеты, связанные с преобразованием гармонических сигналов, значительно
упрощаются, если вместо косинусоидальной гармоники использовать комплексную
экспоненциальную гармонику. Нетрудно заметить, что
действительной части
можно записать в виде
от комплексной гармонической функции координат и
времени
где
58
- комплексный пространственно-временной гармонический сигнал.
Комплексную функцию координат
называют комплексной амплитудой волны, или комплексным оптическим сигналом.
Так как зависимость от времени
амплитуды
известна заранее, то задание комплексной
достаточно для описания светового возмущения.
Поверхность постоянной фазы, в любой точке
времени фаза волны одинакова,
которой в данный момент
называютволновым фронтом. Вообще
говоря, поверхность постоянной фазы в
не совпадает с поверхностью постоянной
амплитуды. При этом говорят, что такая волна неоднородна. Примером неоднородных
волн служат эрмито-гауссовые и лагерро-гауссовые волны на выходе лазера.
Если
операции,
математических
функция
производимые
выкладок
над
символ
в
,
линейны,
опускается,
заменяется комплекснозначной
а
то
в
для
удобства
вещественная
. Тогда вещественная часть
окончательного выражения будет представлять собой изучаемую физическую
величину. Делая переход к комплексным оптическим сигналам, следует помнить, что
фактически физическая величина напряженности
электрического поля в
электромагнитной волне всегда вещественна.
1.2. Интенсивность монохроматической волны
В основе взаимодействия электромагнитного излучения с фоточувствительной
регистрирующей средой лежит экспериментальный факт, состоящий в том, что отклик
среды (величина электрического заряда, плотность почернения единицы объема
галогенидосеребряной среды, степень отбеливания единицы объема фотохромной
среды и т. п.) есть функция энергии, поглощенной единичным объемом и усредненной
за время, большее по сравнению с периодом световых колебаний. Пусть
– вектор
напряженности электрического поля в электромагнитной волне, именуемый для
краткости электрический вектор, В/м, a
– электрическое смещение, Кл/м2.
59
Здесь
– абсолютная диэлектрическая проницаемость среды, в которой
распространяется
волна;
Ф/м –
абсолютная
постоянная свободного пространства (электрическая постоянная);
диэлектрическая
– безразмерная
относительная диэлектрическая проницаемость среды. Из теории Максвелла известно,
что объемная плотность электрической энергии , Дж/м3, т.е. энергии электрического
поля волны, в системе СИ описывается выражением
Тогда усредненное по времени значение
где угловые скобки означают усреднение во времени, а
– интервал времени, по
которому проводится усреднение.
В любой точке световой волны величина и направление потока электрической
энергии за единицу времени через единичную площадку, нормальную к потоку,
определяется вектором Умова-Пойнтинга
В
классической
величину
электродинамике
, Вт/м2, этого
усредненную
по
времени
вектора называют интенсивностью
,
т.е.
поверхностной плотностью лучистого потока в точке
В системе СИ интенсивность
также выражается в
.
Кроме того, на практике для удобства используется сокращенное определение
интенсивности
60
Так как интенсивность
, где
, то всегда можно понять, какая
интенсивность имеется в виду в данной ситуации.
Заметим, что в оптике на практике наряду с поверхностной плотностью лучистого
потока используется
излучения
пространственно-угловая
плотность,
или
сила
. В фотометрии она называется силой света
.
В то же время основной интерес представляет отношение интенсивностей в разных
точках
между
и
и
волнового
поля.
Тогда
благодаря
пропорциональности
отношение интенсивностей в этих двух точках однозначно определяется
любым из двух выражений
В
общем
учетом
случае
электрический
вектор
монохроматической
волны
с
описывается выражением
где
– вектор амплитуды;
Гц.
Подставляя
в
, получим
Откуда при
имеем
Таким образом, преимущество определения интенсивности в виде
состоит в том,
что она определяется скалярным квадратом вектора амплитуды электрического поля,
т. е. квадратом амплитуды.
61
Используя понятия комплексных амплитуд
и
, выражение для интенсивности
монохроматической волны можно представить в виде
Тогда в комплексном представлении интенсивность равна квадрату модуля
комплексной амплитуды.
1.2.1. Случай акустической волны
В любой точке акустической волны величина и направление потока механической
энергии за единицу времени через единичную площадку, нормальную к потоку,
можно определить вектором, аналогичным вектору Умова-Пойнтинга
Усредненную
по
времени
называют интенсивностью
величину
Вт/м2,
этого
вектора
, т.е. поверхностной плотностью потока излученияв
точке.
Лекция 5. Продолжение
1. Однородные плоские монохроматические волны
Любое решение волнового уравнения вида
представляет
времени
собой плоскую
величина
волну,
так
как
в
каждый
момент
постоянна во всех точках плоскости, задаваемой
векторным уравнением в виде скалярного произведения
где
– радиус-вектор точки;
– единичный
вектор
нормали
к
которого определяются направляющими косинусами (рис. 1).
62
плоскости,
координаты
Рис.1.
Трехмерная
геометрическая
модель,
идентифицирующая
процесс
распространения однородной плоской волны в пространстве
Иначе говоря, плоская волна, фаза которой постоянна во всех точках некоторой
плоскости, имеет плоский волновой фронт.
Общее решение волнового уравнения
в виде
волну, которая распространяется в направлении вектора
Аргумент
функции не
величины
и
меняется
соответственно.
при
, выражающее плоскую
со скоростью , имеет вид
замене
Физически
величин
это
и на
означает,
что
возмущение , которое в момент времени было в плоскости, находящейся на
расстоянии
времени
от
начала
оказывается
расстоянии
от
замены нa
координат,
в
начала
в
плоскости,
координат.
поздний
расположенной
Вводя
в
момент
уже
в
на
результате
структуру плоского волнового фронта и учитывая, что для
однородной плоской волны
выражение
более
для
электрического
, получим скалярное комплексное
(магнитного)
монохроматической волны
63
поля
однородной
плоской
где
– длина
волны
в
среде с
показателем
преломления n.
Длину волны
называют приведенной
длиной
волны (соответствует
распространяющейся
в
вакууме монохроматической волне той же частоты).
Вектор
единичного
или
для вакуума
вектора
длину
,
нормали
, направленный вдоль
(рис.
соответственно
1),
для
называютволновым
вакуума
,
вектором.
Его
называют волновым
числом. Волновой вектор является обобщенным пространственным аналогом
временной угловой частоты
Так
.
как
замене
на
выражение
, то
является
не
изменяется
пространственным
при
периодом
плоской
волны. Для задания ориентации пространственных гармонических осцилляции в
плоской волне на практике очень удобно ввести векторы пространственной частоты
направления которых совпадают с направлением распространения , а длины
соответственно равны
Они
задают
число
пространственных
периодов
(осцилляций)
в
волне,
укладывающихся на единице длины, 1/мм, соответственно в среде или в вакууме, и по
аналогии с временной частотой называются пространственными частотами. Это еще
более углубляет аналогию между волновым вектором и угловой частотой .
В
итоге комплексную
амплитуду
однородной
волны можно представить в виде
64
плоской
монохроматической
В
в
расстояния
соответствии
с
фаза
увеличивается
от начала координат, а фаза
с
ростом
уменьшается с ростом
времени . Выбор такого правила знаков в плоской волне обусловлен описанием ее
распространения в направлении вектора . Он не имеет существенного значения, так
как практический интерес представляет не абсолютная величина фазы, а разность фаз.
В то же время в рамках выбранного правила знаков процесс распространения плоской
волны
сводится
плоскости
к
следующему.
согласно
.
времени
полная
расстоянии
от
любой
точки
некоторой
полная фаза волны в момент времени постоянна и
равна
как
Для
фаза
начала
будет
В
иметь
более
то
же
поздний
значение
на
координат
момент
большем
,
, в то время как на прежнем расстоянии
так
она уменьшается. В результате
плоский волновой фронт перемещается в пространстве в направлении, которое в
зависимости от специфики задачи можно охарактеризовать одним из трех
коллинеарных
векторов
пространственной частоты
–
единичным
вектором
или волновым вектором
нормали ,
вектором
(рис. 1).
Таким образом, однородная плоская монохроматическая волна
является тем
важным частным случаем комплексного временного гармонического сигнала
,
который позволяет с единых позиций рассматривать частотно-временные и
пространственно-частотные
гармонические
осцилляции
произвольной
монохроматической электромагнитной волны, представляемой в виде суммы плоских
волн. Это в свою очередь служит первым шагом на пути создания общей частотной
МП ОЭС при описании множества S входных сигналов набором плоских волн. Для
65
описания плоской волны, распространяющейся в противоположном направлении, надо
во
всех
полученных
противоположные
видеть,
заменить
векторы
на
.
Тогда на основании
Нетрудно
выражениях
комплексная амплитуда примет вид
что
противоположному
направлению
распространения
соответствует комплексно-сопряженная амплитуда. В этом, в частности, проявляется
одно из преимуществ введения комплексного оптического сигнала. Другое
преимущество использования комплексной амплитуды выясняется при переходе к
координатному представлению однородной плоской монохроматической волны.
Вектор
пространственной
плоскостной
периодической
пространственно-частотной
частоты
перпендикулярен
решетке,
состоящей,
гармоники,
которая
например,
из
соответствует
трехмерной
максимумов
комплексной
амплитуде плоской волны в фиксированный момент времени и тем самым задает ее
ориентацию.
66
Рис.2. Двумерная геометрическая модель, идентифицирующая пространственночастотную структуру плоской волны
На рис. 2 приведена решетка с вектором , лежащим в плоскости , так что ее
реберные
учетом
грани
перпендикулярны
этой
плоскости
(параллельны
оси ).
С
координаты
называют координатными пространственными частотами соответственно вдоль
осей
. Если направление распространения
(или ) составляет с какой-либо
осью угол меньше 90°, то соответствующая координатная пространственная частота
положительна. Если угол больше 90°, то частота отрицательна. В оптике
координатные пространственные частоты часто выражаются через дополнительные
углы
что
(углы
падения)
так
.
67
Тогда, переходя в
к координатной форме записи скалярного произведения
,
получим
В частности, плоская волна, распространяющаяся в направлении
параллельном плоскости
,
( = 90°, рис. 2), имеет в произвольной точке
комплексную амплитуду
При
получим
точке
выражение
для
комплексной
в
плоскости
Наконец, если
, то комплексная амплитуда плоской волны,
распространяющейся в направлении оси , в точке
а в точке
амплитуды
имеет вид
она будет
Оптико-физический смысл координатных пространственных частот заключается в
том, что их знаки определяют направление распространения плоской волны, а
численные
периодам
значения
обратно
трехмерной
пропорциональны
плоскостной
решетки
вдоль
пространственным
соответствующих
координатных
осей
.
68
Для
волны,
вектором
,
распространяющейся
лежащим
в
I
в
направлении
квадранте,
(рис.
частоты
что
так
и
определяют пространственные периоды плоских решеток,
которые получаются в сечениях трехмерной решетки плоскостями
квадранта
На основании
с
.
В этом случае
IV
2)
,
для
III
квадранта
и
,
. Для II
а
для
.
и
координатные пространственные частоты в плоской
волне связаны соотношением
откуда
, где знак определяется знаком
.
Тогда можно описать процесс распространения комплексной амплитуды плоской
волны в пространстве, если выразить
через
где
.
В результате комплексная амплитуда плоской волны
на произвольном
расстоянии от начала координат оказывается равной произведению комплексной
амплитуды
в плоскости
на комплексную экспоненциальную функцию
распространения [см.(2.18)]
описывающую фазовую пространственно-частотную дисперсию. В соответствии с
выбранным правилом знаков с ростом фаза волны увеличивается. Как показано в 2.2.2
(см. 2.18) это выражение идентифицирует когерентную передаточную функцию
когерентного слоя свободного пространства.
69
2. Однородные сферические монохроматические волны
Сферической волной называют любое решение волнового уравнения
где
вида
.
Иначе говоря, в случае сферической волны величина
постоянна на сфере
. Общее решение
в каждый момент времени
, выражающее сферическую
волну, расходящуюся от начала координат, имеет вид
.
Множитель выражает закон сохранения энергии при распространении сферической
волны и учитывает, что интенсивность сферической волны
остается
постоянной
поверхности сферы, а
в
процессе
распространения.
замены на
—
площадь
– символ пропорциональности.
Скалярное комплексное выражение для
расходящейся
Здесь
монохроматической
электрического поля
волны
получается
, так что с учетом однородности
из
сферической
в
результате
имеем
.
Откуда
комплексная
амплитуда
однородной
сферической
расходящейся
монохроматической волны
Так как общее выражение для сферической волны, сходящейся к началу координат,
имеет вид
то комплексно сопряженная амплитуда
70
соответствует однородной сферической сходящейся монохроматической волне.
Сравнение выражений
и
показывает, что плоская и сферическая волны
локально похожи друг на друга. В самом деле, на достаточно большом расстоянии от
начала координат в некоторой малой окрестности можно приближенно считать, что,
например,
векторы
и
коллинеарны, так
локальное совпадение комплексных амплитуд
В
окрестности
рассматривать
знаменателе
некоторой
в
оси,
параксиальном
что
.
и
и
означает
.
например ,
приближении.
Это
сферическую
В
этом
волну
случае
удобно
величину
в
можно приближенно заменить на , а в фазовом множителе
разложить по биному Ньютона
.
Тогда для комплексной амплитуды имеем
Таким образом, в параксиальном (квадратичном) приближении сферическая волна
аппроксимируется параболической волной.
Когерентное, частично-когерентное и некогерентные приближения
Когерентное приближение
При анализе поведения ОЭС, и в некоторых случаях, РЭС, прежде всего вводится
предположение
о
строгой
монохроматичности
используемого
излучения.
Монохроматические волны, по определению, имеют бесконечную продолжительность
во времени. Это очень жесткое ограничение, так как в лучшем случае излучение
реальных источников, включая лазеры, является только квазимонохроматическим, т. е.
состоящим из спектральных компонент, которые занимают частотный диапазон
малый по сравнению со средней временной частотой
излучения
определяет
,
. Монохроматичность
его временную или продольную
71
когерентность (согласованность). При этом излучение считается когерентным во
времени, если разность фаз в фиксированной точке
так что
не меняется с течением времени,
. В этом случае распределение интенсивности в
интерференционном поле (интерференционная структура) равно интенсивности
суммарной
волны
с
учетом
фазовых
соотношений.Степень
временной
когерентности определяется путем измерения времени или длины когерентности
по видности (контрасту)
интерференционной
структуры
в
интерферометрах
с
делением по амплитуде, когда весь волновой фронт участвует в формировании каждой
из интерферирующих волн.
Точечный монохроматический источник в интерферометрах с делением по
волновому фронту, в которых интерферирующие волны образуются из разных
участков исходного фронта, формирует интерференционную структуру с видностью,
равной единице. В случае источника конечных размеров, состоящего из независимых
точечных монохроматических источников, интерференционная структура имеет
меньшую видность, которая характеризует степень пространственной или поперечной
когерентности излучения.
При
этом
излучение
когерентным, если разность фаз в любых двух точках
времени, так что
считается пространственнои
не меняется с течением
. К пространственно-когерентному
излучению близко излучение одномодовых лазеров.
В общем случае излучение называют абсолютно когерентным, если разность фаз в
любых точках
и
остается постоянной в любые моменты времени
что
Примером
и
, так
.
абсолютно
когерентных
оптических
сигналов
являются
идеализированные плоские и сферические монохроматические волны (2.4.3.1).
Абсолютно когерентного излучения в природе не существует, но к этому пределу
(видность интерференционной структуры очень близка к единице) можно подойти
вплотную в специальном случае одночастотной генерации в лазере. Хотя без
специальных излучателей этот случай представляется лишь идеализацией, но
72
результаты, которые получаются на основании идеализированного представления об
абсолютной
когерентности,
могут
быть
с
достаточной
степенью
точности
использованы на практике.
Поэтому при анализе пространственных преобразующих систем (ППС) в ОЭС И
РЭС прежде всего выделяют пространственные фильтры (ПФ) ОЭС И РЭС
с когерентным поведением. Произвольный ПФ в узком, широком или общем смысле,
работающий при абсолютно когерентном освещении и линейный относительно
комплексной амплитуды поля, называется когерентным фильтром (КФ). Одной из
основных
внешних
характеристик
связность
КФ
является
интерференционного поля
регистрации в КФ интенсивность
линейная
. Тогда при его
в плоскости наблюдения определяется квадратом
модуля суммарной комплексной амплитуды и, в случае двух волн, имеет вид
где последнее слагаемое представляет собой интерференционный член, зависящий
от разности фаз. Если в плоскости наблюдения складываются
когерентных волн, то
для суммарной амплитуды и интенсивности получим
В общем случае для непрерывного распределения комплексной амплитуды сумма
превращается в интеграл суперпозиции для распределения комплексной амплитуды.
Частично когерентное приближение
Статистический характер изменения амплитуды и фазы оптического излучения в
плоскости объекта может сильно влиять на преобразующие свойства ОЭС И РЭС.
Если изменения амплитуды и фазы во времени носят случайный характер, то поле
удовлетворительно описывается только при помощи осредненных характеристик.
Поэтому
в
общем
случае
говорят
о
ПФ
ОЭС
и
РЭС
с частично
когерентным поведением. Такая ОЭС И РЭС или произвольная ОС в узком, широком
или общем смысле, работающая при частично когерентном освещении и линейная
73
относительно функции взаимной когерентности или взаимной интенсивности,
называется частично когерентным фильтром (ЧКФ).
В ЧКФ каждая точка объекта обусловливает определенное распределение
комплексной амплитуды поля в плоскости наблюдения. Когда амплитуда и фаза в
точках
и
объекта изменяются случайным образом, то также будет изменяться
амплитуда и фаза в точке
плоскости наблюдения. Следовательно, статистическая
связность
пространственно-временными
между
сигналами
и
гармоническими
в разных точках объекта будет обусловливать
статистическую связность
между их образами
и
в точке
плоскости
наблюдения. Наличие такой статистической связности влияет главным образом на
интенсивность
, которая получается в результате усреднения во времени имеет
вид
где
и
точек
и
- комплексные постоянные, обусловленные распространением волн от
к
точке ;
-
время
задержки
первой;
второй
- функция
волны
взаимной
относительно
когерентности,
которая определяется по одной реализации как функция взаимной ковариации
стационарных эргодических полей;
Вводя в рассмотрение комплексную степень когерентности
получим общий
закон
интерференции
для
электромагнитных полей.
74
стационарных
эргодических
где в отличие от
интерференционный член полностью определяется степенью
когерентности. При этом из
следует, что ЧКФ линеен относительно функции
взаимной когерентности. В случае квазимонохроматического источника со средней
оптической частотой
комплексную степень когерентности можно представить в
виде
где
, так что закон интерференции
Величину
примет вид
называют степенью когерентности колебаний в точках
и
.
Она определяет видность интерференционной структуры
Если интенсивности обеих волн совпадают
когерентности
.
Когда
, то видность равна степени
достигает
значения, равного единице, интенсивность
монохроматических
волн
фаз
своего
максимального
, которая получилась бы для
со
средней
будет
совпадать
частотой
с
в
и
.
разностью
Этот
случай
соответствует уже рассмотренным абсолютно когерентным волнам, выходящим из
точек
и
Если
,
при
определенном
времени
задержки
между
ними.
, то и видность лежит в этом диапазоне, а сигналы оказываются
частично когерентными.
На практике, особенно это имеет место в случае лазерного излучения, время
задержки
одной интерферирующей волны относительно другой часто много меньше
времени когерентности, так что
результате
при
, где
функции
– ширина полосы излучения. В
и
75
незначительно
отличаются от своих значений в нуле
выражение
и
. Тогда
приближенно можно представить в виде
где
–
когерентности
при
нулевой
задержке.
комплексная
Выражение
является
степень
основной
формулой элементарной (квазимонохроматической) теории частичной когерентности.
Величину
характеризующую взаимную ковариацию между колебаниями в любых двух
точках и волнового поля, называют взаимной интенсивностью. Она зависит только
от
положения
этих
точек,
но
не
как
зависит
то
от
ЧКФ
времени
задержки .
приближённа
Так
линейна
относительно взаимной интенсивности.
Некогерентное приближение
Если в выражении
нулю, то и видность
достигает своего минимального значения, равного
интерференционной структуры также равна нулю. Тогда не
возникает никаких интерференционных эффектов от наложения волн в плоскости
наблюдения и излучение считается некогерентным. Практически такое излечение
формирует
протяженный
полихроматический
источник,
который
можно
рассматривать как ансамбль статистически независимых точечных источников.
В соответствии с этим выделяется ПФ с некогерентным поведением. Такой
произвольный ПФ в узком, широком или общем смысле, работающий при
некогерентном
освещении
и
линейный
относительно
интенсивности,
называют некогерентным (НКФ). Одним из основных внешних свойств НКФ является
линейная связность
интерференционной структуры, которая
76
вытекает из
. В самом деле, при нулевой степени когерентности в случае двух волн
в плоскости наблюдения имеем
Это следует также из общего закона интерференции
в предположении, что
разность фаз в интерференционном члене, определяемая
, для ансамбля
статистически независимых источников с равной вероятностью принимает все
значения на
. Тогда с учетом
интерференционный член равен нулю.
Если в плоскости наблюдения складываются
некогерентных волн, то для
суммарной интенсивности получим
В
общем
случае
для
непрерывного
распределения
интенсивности
сумма
превращается в интеграл суперпозиции для распределения интенсивности.
Лекция 6.
Дифракционный интеграл
Параксиальное приближение для сферической волны имеет место в том случае,
когда
При
.
Поэтому
комплексная амплитуда сферической волны в параксиальном приближении
Проанализируем дифракцию световой волны на транспаранте
транспарант имеет амплитудное пропускание
При
непосредственно
за
транспарантом
77
Первый член данного выражения описывает плоскую волну, распространяющуюся
вдоль оси , как и падающая волна, второй и третий члены - плоские волны,
направления
распространения
причем
которых
с
осью составляют
углы
и
,
(рис.4). Таким образом, в результате дифракции часть
падающей на транспарант световой волны отклоняется от первоначального
направления распространения.
Рис. 3 Связь между координатами сферической и прямоугольной систем координат
78
Рис. 4 Дифракция плоской волны на синусоидальной дифракционной решетке
С помощью соотношения для плоской волны можно определить комплексную
амплитуду света при любом удалении от транспаранта, например при
Для первого члена выражения
Из
следует, что если
затухающими при
решетки,
.
, то возникают поверхностные волны. Они будут
, т.е. когда длина волны больше периода дифракционной
поскольку
а
, для второго и третьего членов
при
-
этом
становится
экспоненциальным
мнимой
множителем,
величиной,
убывающим
с
увеличением .
Амплитудное пропускание двумерной дифракционной решетки в общем случае
описывается комплексной периодической функцией двух переменных
и . Однако
его также легко представить в виде суммы простейших синусоидальных функций
путем разложения в ряд Фурье [2]:
79
Дифрагированная на таком транспаранте световая волна представляет собой
суперпозицию бесконечного числа плоских волн с амплитудами, пропорциональными
соответствующим коэффициентам разложения
определяемыми
и
и направлениями распространения,
Следовательно, суммарная амплитуда
дифрагированных волн в плоскости
Рис.5. К решению задачи дифракции с помощью интеграла Френеля-Кирхгофа
В общем случае амплитудное пропускание дифрагирующего объекта является
комплексной непериодической функцией двух переменных x и y, поэтому t (x, у)
заменяют интегралом Фурье. Комплексную амплитуду дифрагированной волны в
плоскости z = d при этом также выражают с помощью интеграла
80
( 5’)
где
- преобразование Фурье от
, причем интегрирование производят в
области, удовлетворяющей неравенству
(вне этой области волны
быстро затухают при удалении от транспаранта). Следовательно, можно сделать
следующее заключение: если плоская волна амплитудой
, распространяющаяся в
направлении оси , падает на помещенный в плоскости
амплитудной функцией пропускания
плоскости
Для
транспарант с
, то спектр комплексной амплитуды в
имеет вид
параксиальных
волн
приближением
значениях и , выражение
Ввиду того, что фаза
,
пользуясь
, справедливым при малых
можно представить следующим образом:
в выражении
является параболической
функцией пространственных частот, это приближение называют параболическим.
Согласно правилу Рэлея искажение фазы волны не должно превышать
устанавливаются границы применимости параболического приближения:
81
, т.е.
Решение задачи дифракции можно представить также с помощью интеграла
Френеля-Кирхгофа :
где
(рис 5);
и
Угол
прямой
расстоянии
Интеграл
- координаты точек, принадлежащих плоскостям
между
положительным
называют коэффициентом
от
плоскости
дфракции
направлением
наклона.
дают
и
оси
.
и
Формулы
один
и
тот
отрезком
5’ и
же
на
результат.
является матматическим выражением известного принципа Гюйгенса-
Френеля.
1. Дифракционные формулы Френеля и Фраунгофера
Рассмотрим дифракцию света, падающего на непрозрачный экран с отверстием
произвольной формы. Отверстие в экране называют апертурой. В зависимости от
удаленности источника света и плоскости наблюдения от дифрагирующего экрана
различают зоны дифракции Фраунгофера и Френеля. Дифракция Фраунгофера
наблюдается в дальней зоне, удаленной от дифрагирующего экрана на расстояние, во
много раз превышающее размеры апертуры. Дифракция Френеля имеет место в
ближней зоне, распространяющейся до зоны дифракции Фраунгофера, как это
показано на рис.6. Дифракция Фраунгофера по существу является предельным
случаем дифракции Френеля при больших расстояниях от экрана. Заметим, что зона
дифракции Френеля также начинается на некотором расстоянии от экрана.
Непосредственно за апертурой вблизи экрана находится область тени (рис.6). Здесь и
далее будем предполагать, что размеры отсверстия на экране велики по сравнению с
длиной волны падающего света, а источник света находится на таком расстоянии от
экрана, что свет, падающий на экран, имеет практически плоский волновой фронт и
постоянную амплитуду. В общем случае апертура представляет собой транспарант с
82
двумерной амплитудной функцией пропускания
. В частном случае апертура
является отверстием с амплитудной функцией пропускания
Данный случай важен, поскольку часто встречается при анализе оптических систем
хранения и обработки информации [3,4]. В любом из рассмотренных случаев
непосредственно за экраном при
световое поле описывается распределением
амплитуд
83
Рис.6. Зоны дифракции Фраунгофера и Френеля
Свет,
падающий
амплитуду
на
Тогда
экран,
также
световое
имеет
поле
произвольную
имеет
за
экраном
комплексную
комплексную
амплитуду:
В дальнейшем будем считать, что непосредственно за экраном световое поле имеек
комплексную амплитуду
. Поэтому интеграл Френеля-Кирхгофа
для
рис.6 можно записать в виде
где
1.1. Приближение Френеля
Для дифракционного поля в области, удаленной от экрана на расстояние,
значительно превышающее максимальный размер апертуры, интеграл ФренеляКирхгофа
значительно упростится. Действительно, если
то можно полагать, что
Расстояние
с ошибкой менее
в знаменателе подынтегрального выражения
, если угол
.
можно заменить
координатой , поскольку
и
выражение
согласно
неприемлемо для замены
.
Однако
в экспоненциальном члене, так как на
экспоненту влияет даже малое изменение
. Для получения более точного
приближения воспользуемся разложением
.
Учитывая первые два члена данного разложения для аппроксимации квадратного
корня, примем
84
С учетом
интеграл Френеля-Кирхгофа можно записать в следующем
упрощенном виде:
Данное выражение называют приближением Фреленя, а соответствующее ему поле
- дифракционным полем Френея. Интегральное преобразование вида
где
называют преобразованием
Френеля
представляет
Френеля.
собой
Следовательно,
двумерное
приближение
преобразование
Френеля
дифрагировавшего на экране светового поля. Приближение Френеля справедливо в
зоне [3]
где
- максимальный радиус апертуры;
- максимальный радиус области наблюдения в плоскости (см. рис. 6);
- наименьшая неоднородность распределения светового поля
связанная с максимальной пространственной частотой поля
,
.
1.2. Приближение Фраунгофера
Ранее отмечалось, что дифракция Фраунгофера является предельным случаем
дифракции Френеля при больших значениях , т.е. в дальней зоне. При этом можно
принять более жесткое допущение, нежели чем
, а именно
85
Рассмотрим
допущения
формула
приближение
можно
Френеля,
записанное
в
принять
виде
.
Тогда
С
учетом
дифракционная
еще более упроститься:
Полученное
приближение
являющегося
имеет
преобразованием
амплитуд
света,
основной
Фурье
множитель
в
виде
распределения
дифрагировавшего
на
экране,
интеграла,
комплексных
и
его
называют приближением Фраунгофера. Такоим образом, дифракция Фраунгофера
представляет собой фурье-образ светового поля, дифрагировавшего на экране,
умноженный
на
квадратичный
фазовый
множитель
.
Если
интересующая область в плоскости наблюдения дифракции Фраунгофералежит вблизи
оси , так что выполняется условие
или
то
В последнем случае приближение Фраунгофера упрощается:
Зона дифракции Фраунгофера определяется из условия [3]
Если
мкм;
условие
см.
мкм, то зоне дифракции Фраунгофера соответствует
1.3 Приближение тени
Если требуется определить поле вблизи экрана, то используют приближение тени:
86
справедливое при [3]
Лекция 7
Оптические системы, выполняющие преобразование Фурье
С помощью сферической линзы можно создавать картину, являющуюся фурье-образом входного
изображения. Благодаря этому устройству, а также возможности применения линз для формирования
пучков излучения требуемой конфигурации они находят широкое применение в оптических системах
хранения и обработки информации.
Рассмотрим простейшую оптическую систему (рис. 1), состоящую из одной тонкой сферической
линзы с фокусным расстоянием f помещенной в плоскости z = 0, и расположенного вплотную к ней
транспаранта с комплексным амплитудным пропусканием
t (х0, у0).
Линзу называют тонкой, если луч, входящий в точку с координатами (x0, y0) выходит из нее на
противоположной поверхности в точке примерно с теми же координатами. Это означает, что смещением
луча внутри линзы можно пренебречь: линза задерживает фронт падающей волны на значение,
пропорциональное толщине линзы в каждой точке. Следовательно, тонкую линзу можно рассматривать
87
как транспарант, осуществляющий фазовую модуляцию и имеющий функцию пропускания вида
, где функция Δφ(х, у) пропорциональна толщине линзы в точке с координатами
(х, у). Нетрудно показать, что
(1)
{Таким образом, свет в тонкой линзе проходит оптический путь, пропорциональный
толщине линзы в данной точке. Обратимся к рис. а. Проведем две параллельные
плоскости, прижатые к линзе с обеих сторон. Луч А проходит через линзу оптический
путь n0 (где п —- показатель преломления материала линзы; 0 — ее максимальная
толщина), а луч В часть пути между плоскостями проходит в воздухе, а часть — в
стекле, поэтому пройденный им оптический путь равен п(х, у) - (0 - (х, у)), где (х,
у) — толщина стеклянной части линзы в соответствующей точке.
Рис. а. Линза как фазовая задержка
Этому оптическому пути соответствует изменение фазы световой волны, равное
Тогда коэффициент пропускания линзы как объекта, сформированного двумя
88
параллельными плоскостями,
(1.1)
При этом мы учли, что линза абсолютно прозрачна, поэтому коэффициент
амплитудного пропускания равен единице, а все изменения содержатся в показателе
экспоненты.
Необходимо определить значение (х, у). При этом мы будем учитывать правило
знаков: радиус кривизны поверхности считается положительным, если эта поверхность
выпуклая для луча, идущего слева направо. Разделим линзу на две части (см. рис. а) и
проанализируем их по отдельности.
Представим
толщину
линзы
как
сумму
толщин
двух
ее
половинок
(x,y)=1(x,y)+2(x,y). Каждая из этих величин может быть выражена через
соответствующий радиус кривизны, как это видно из рис. а:
В уравнениях учитывался знак радиусов кривизны.
Складываем полученные величины и получаем толщину линзы в произвольной
точке
(1.2)
Будем рассматривать только лучи, идущие под небольшими углами к оси линзы
(параксиальное приближение), поэтому в (1.2) корни можно разложить в ряд, оставив
только нулевой и первый члены ряда
Подставляя это разложение в (1.2), получаем
89
(1.3)
Теперь преобразуем к явному виду (1.4)
Воспользовавшись формулой линзы, окончательно получим
}
Таким образом, соответствующее тонкой сферической линзе комплексное пропускание
(2)
Допустим, что на рассматриваемую оптическую систему (рис. 1) падает плоская волна
амплитудой A0, распространяющаяся в положительном направлении оси z. Комплексная амплитуда
света непосредственно вблизй линзы справа от нее равна произведению функции пропускания
транспаранта и линзы:
(3)
Далее волна распространяется в свободном пространстве, поэтому комплексная амплитуда света
на любом расстоянии от линзы может быть рассчитана с помощью интеграла Френеля — Кирхгофа.
Для расчета распределения комплексных амплитуд света на расстоянии z = d от линзы
воспользуемся приближением Френеля
Тогда
(4)
Интегрирование производят по всей поверхности линзы. Подставим в (4) выражение (3), опустив
несущественный для дальнейшего анализа постоянный фазовый множитель
ехр (— ikd),
90
(5)
В результате упрощения данного интеграла путем разложения квадратов (х — х0)2 и (у — y0)2 ,
получим
(6)
Если d = f т. е. рассматривается распределение комплексных амплитуд света в задней фокальной
плоскости линзы, то выражение (6) еще более упрощается и принимает следующий вид:
(7)
где
.
Интеграл в данном выражении представляет собой двумерное преобразование Фурье функции t
(х, у) при условии, что функция t (х, у) тождественно равна нулю за пределами поверхности линзы. Это
условие позволяет расширить пределы интегрирования до бесконечности, что и требуется для
преобразования Фурье.
Таким образом, если на тонкую сферическую линзу с примыкающим к ней транспарантом падает
плоская световая волна,то в задней фокальной плоскости линзы образуется поле с распределением
комплексных амплитуд, пропорциональным произведению квадратичного фазового множителя и фурьеобраза функции пропускания транспаранта.
В тех случаях, когда важна только интенсивность света, квадратичный фазовый множитель в
выражении (1.48) не учитывают.
Эффект, обусловленный этим множителем, эквивалентен действию тонкой рассеивающей
(вогнутой) линзы с фокусным расстоянием - f, помещенной в плоскости z =f. Если в плоскость z=f
91
поместить тонкую собирающую линзу с фокусным расстоянием f то этот фазовый множитель будет
компенсирован. В результате получают оптическую систему (рис. 1.8), выполняющую точное преобразование Фурье:
Предполагается, что за пределами поверхности транспаранта t (х, у) == 0. Если линза имеет
неограниченные размеры, а транспарант совершенно прозрачен, т. е. t (х, у) =1, то
Следовательно, падающая на линзу плоская световая волна фокусируется в точку на задней
фокальной плоскости линзы. Линза конечных размеров образует световое пятно малых, но все же
конечных размеров, что и наблюдается на практике.
Анализ методов цифровой голографии
Анализ
проведен
с
учетом
задачи
построения
комбинированного
стеганографического метода защиты изображений. Направление анализа обусловлено
тем, что ставится задача использовать известных методы обработки изображений для их
защиты. Одним из основных подходов для получения оптических голограмм является
добавление к световой волне, рассеянной объектом, опорной волны. Цифровые
голограммы Фурье представляют собой запись пространственного преобразования Фурье
92
от рассеянного предметом светового поля со сдвинутой пространственной несущей. В
общем случае голограмму можно представить как комплексную функцию. Комплексное
преобразование
Фурье
от
функции,
описывающей
распределение
контраста
в
изображении водяного знака W’(u,v) в плоскости записи голограммы представим в
форме: w( x, y) w( x, y) exp( j( x, y)) , где Ф(x,y) – аргумент комплексной функции w(x,y).
Добавим к волновому полю w(x,y) опорную когерентную волну exp{ j ( xM yN )} , где M и
N – углы падения волны по нормали к плоскости регистрации голограммы.
Распределение интенсивности в плоскости регистрации представляет собой квадрат
модуля суммы волнового поля w(x,y) и опорной волны:
2
h( x, y ) w( x, y ) exp{ j( x, y)} exp{ j ( xM yN )} w( x, y)
2
w( x, y ) cos xM yN ( x, y ) 1.
Первый член в этом выражении характеризует дополнительную засветку голограммы
пучком света от объекта и обычно опускается. Этот член не содержит фазовой
характеристики и не несет никакой информации о восстановленном изображении.
Следовательно, получаем:
h( x, y) A0 w( x, y) cos xM yN ( x, y) ,
где постоянная составляющая A0 – максимальное значение w(x,y)=w(0,0). Таким
образом, функция h(x,y) является вещественной, положительной и содержит полную
информацию (как амплитудную, так и фазовую) об изображении ЦВЗ W(u,v).
Преобразование Фурье от полученной функции голограммы h(x,y) будет состоять из
суммы двух изображений водяного знака W(u,v), смещенных относительно начала осей
координат на величины несущих частот M и N:
h( x, y) W (u, v) W (u M , v N ) W (u M , v N ) A(u, v) ,
где – оператор Фурье-преобразования, A(u,v) – автокорреляционная функция ЦВЗ.
Автокорреляция A(u,v) располагается в начале координат и подавляется как в цифровой
голографии, так и в оптической. Второе изображение W(-u-M,-v-N) является зеркальным
отображением W(u-M,v-N) относительно центра осей координат.
Алгоритм синтеза изображения ЦВЗ для получения голограммы h(x,y):
93
1)
В предметной области (x,y) изготавливается изображение ЦВЗ W(x,y);
2)
ЦВЗ переносится в плоскость пространственных частот (u,v) со смещением
относительно осей координат на значения M, N: W(u-M,v-N);
3)
Создается зеркальное изображение ЦВЗ и получается сумма двух изображений:
h( x, y) W (u, v) W (u M , v N ) W (u M , v N ) , где γ – коэффициент усиления;
4)
Для
получения
исходного
распределения
h(x,y)
выполняется
обратное
преобразование Фурье: h( x, y ) 1 W (u, v) , где 1 – оператор обратного преобразования
Фурье. Следует отметить, что предельные размеры изображения ЦВЗ не должны
превышать размеры квадранта
произойдет
перекрывание
частотной плоскости. Так как в противном случае
сигналов
W(u-M,v-N)
и
W(-u-M,-v-N).
При
выборе
оптимального размера ЦВЗ необходимо учитывать заметность вносимых возмущений в
изображение-контейнер и устойчивость ЦВЗ к искажениям. Другим важным фактором
выбора размера ЦВЗ является функция передачи модуляции (ФПМ) сквозного оптикоэлектронного тракта, включающего фотопринтер, фотоноситель и сканер на ПЗС (прибор
с зарядовой связью (CCD)). Размеры W(u,v) должны укладываться в области определения
ФПМ сквозного тракта. Это означает, что функция W(u,v) должна быть узкополосной.
В
радиотехнике
с
целью
повышения
эффективности
передатчиков
широко
применяется метод передачи сообщений с одной боковой полосой (ОБП), при этом,
вторая боковая полоса и несущая подавляются. Следовательно, чтобы избежать
избыточности
представления
водяного
знака
W (u, v) ,
целесообразно
поступить
аналогично. Тогда h( x, y) 1 W (u M , v N ) , где h(x,y) – комплексная голограмма,
которая состоит из вещественной и мнимой частей:
h( x, y ) hc ( x, y ) jhc ( x, y )
1
j
w( x, y ) cos xM yN w( x, y ) sin xM yN A0 .
2
2
Так как спектральные сигналы W(u,v) должны быть узкополосными, первые два члена
этого выражения связаны между собой преобразованием Гильберта (разложение на
амплитудную и фазовую составляющие). Для восстановления W (u, v) из голограммы
94
будет достаточно выполнить преобразование Фурье только вещественной (косинусной),
или только мнимой (синусной) части комплексной голограммы h(x,y).
Обратное преобразование Фурье для восстановления изображения ЦВЗ, для этого
случая будет иметь вид:
1
1
1 h( x, y ) W (u M , v N ) W (u M , v N ) A(u , v) .
2
2
95
