Индекс концентрации доходов Джини , в отличие от этих

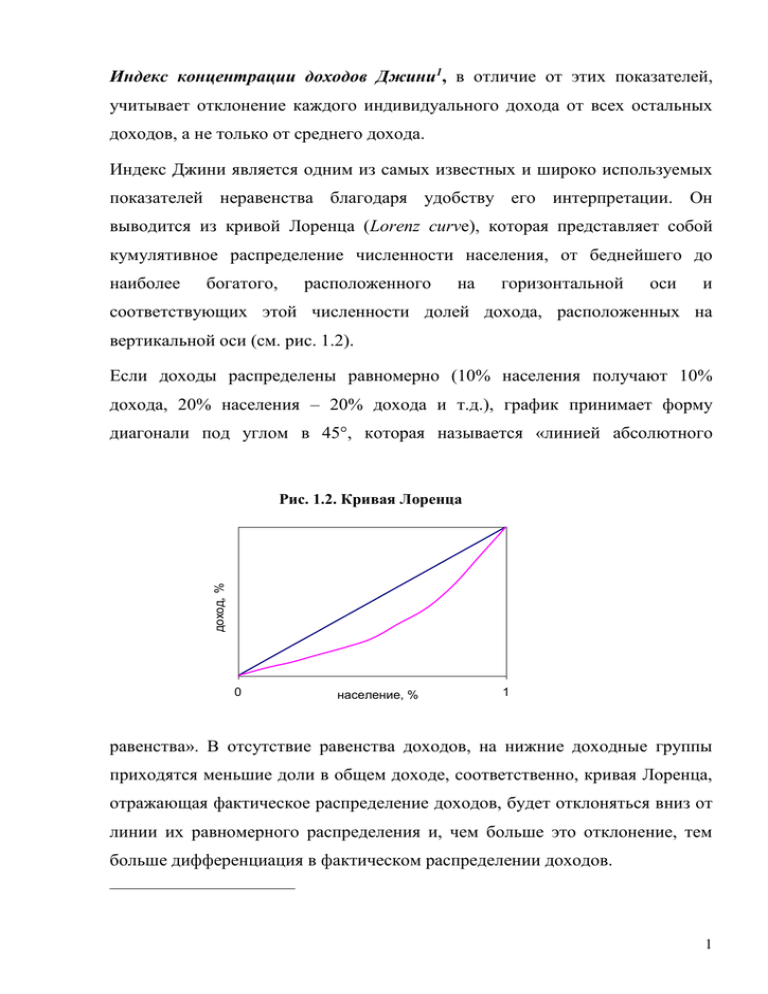
Индекс концентрации доходов Джини1, в отличие от этих показателей,
учитывает отклонение каждого индивидуального дохода от всех остальных
доходов, а не только от среднего дохода.
Индекс Джини является одним из самых известных и широко используемых
показателей неравенства благодаря удобству его интерпретации. Он
выводится из кривой Лоренца (Lorenz curve), которая представляет собой
кумулятивное распределение численности населения, от беднейшего до
наиболее
богатого,
расположенного
на
горизонтальной
оси
и
соответствующих этой численности долей дохода, расположенных на
вертикальной оси (см. рис. 1.2).
Если доходы распределены равномерно (10% населения получают 10%
дохода, 20% населения – 20% дохода и т.д.), график принимает форму
диагонали под углом в 45°, которая называется «линией абсолютного
доход, %
Рис. 1.2. Кривая Лоренца
0
население, %
1
равенства». В отсутствие равенства доходов, на нижние доходные группы
приходятся меньшие доли в общем доходе, соответственно, кривая Лоренца,
отражающая фактическое распределение доходов, будет отклоняться вниз от
линии их равномерного распределения и, чем больше это отклонение, тем
больше дифференциация в фактическом распределении доходов.
1
Коэффициент Джини представляет собой отношение площади между кривой
Лоренца и линией абсолютного равенства к площади треугольника, лежащей
под линией абсолютного равенства. Он принимает значения от 0 до 1 (0 в
случае абсолютного равенства в распределении доходов, 1 – в случае
абсолютного неравенства). Возрастание значения индекса Джини указывает
на рост неравенства.
Индекс Джини может быть представлен как среднее отклонение каждой
доходной единицы в выборке от всех остальных доходных единиц,
выраженное в отношении к среднему доходу:
Gini 
1 n n
 yi  y j
2n 2  i 1 j 1
(1.9)
Где n – число доходных пар,  - средний доход в анализируемом доходном
распределении.
Значение индекса Джини интерпретируется следующим образом: если
показатель равен 0.400, это означает, что разница между двумя случайно
выбранными доходами составляет 80% от среднего дохода.
Класс Обобщенных Энтропийных мер неравенства
В 1967 г. Тейл в своей книге «Economics and Information Theory»
(«Экономика и теория информации») предложил энтропийный индекс
неравенства, основанный на применении к измерению неравенства понятия
энтропии из теории информации (см. Theil 1967). Преимущество данного
индекса заключается в том, что он в отличие от всех рассмотренных ранее
индексов неравенства, выполняет аксиому декомпозиции, то есть может
четко раскладываться на межгрупповую и внутригрупповую компоненты,
которые в сумме будут равны значению агрегированного индекса.
2
Представление Тейлом нового показателя неравенства вызвало появление
множества работ, среди которых первыми и самыми известными стали
работы английских экономистов Бургиньона (Bourguignon 1979), Э.
Шоррокса (Shorrocks 1980) и Кауэлла (Cowell 1980). В своих статьях авторы
сформулировали и математически доказали, что меры неравенства, которые
выполняют требования всех пяти аксиом неравенства, то есть остаются
неизменными в следующих случаях: 1) в случае любых перестановок
доходов между доходными единицами в выборке; 2) повторения выборочных
распределений; 3) пропорционального изменения всех уровней дохода в
выборке; 4) увеличивается в случае трансферта от более бедной доходной
единицы к более богатой,
5)
а также удовлетворяют принципу
декомпозиции, - принадлежат к классу Обобщенных Энтропийных мер
неравенства (Generalised Enthropy Class).
Формула для класса Обобщенных Энтропийных мер неравенства имеет
следующий вид:
1
GE( )  2
 
1 n  y
 i 1  i
 n




  1 ,


(1.15)
где n – число наблюдений в выборке, yi - доход i-ого индивида,   (1/ n) yi
- средний доход в выборке.
Энтропийные меры принимают значения в интервале от 0 до , где 0
представляет полное равенство в распределении доходов, а рост значения
индекса означает рост неравенства в распределении доходов.
Параметр  в формуле для класса Энтропийных мер неравенства – это вес,
который придается доходным трансфертам на различных участках доходного
распределения, данный параметр может принимать любые положительные
значения. Для любого индекса GE(), эффект регрессивного трансферта
зависит не только от уровня доходов отдающего и получающего индивида, и
от среднего дохода в распределении, но и от значения параметра . Чем ниже
3
значение , тем чувствительнее индекс неравенства к трансфертам на
нижнем конце распределения, чем выше значение , тем чувствительнее
индекс к трансфертам на верхнем конце распределения. Чаще всего
используются значения параметра  = 0, 1 и 2.2 Индекс неравенства с
параметра  = 2, GE(2) является «трансфертно нейтральным», поскольку
одинаковый размер трансферта между двумя индивидами, находящимися на
одинаковом расстоянии друг от друга, имеет один и тот же вес на всех
доходных уровнях.3 Все индексы неравенства с параметром  < 1 придают
больший вес трансфертам на нижнем конце распределения (Сен 1997).
В случае  = 1 индекс GE() становится Энтропийным индексом Тейла:
GE(1)
yi
1 n yi
log
;

n i 1 

(1.16)
Когда  = 0, GE() представляет собой второй индекс Тейла (также
известный как среднее логарифмическое отклонение):
GE(0)
1 n

log ;

i 1
n
yi
(1.17)
При  = 2 GE() равен коэффициенту вариации CV2.
1
1 1 n
2
GE(2)   i 1 ( yi   ) 2  ;
 n

(1.18)
Если параметр 1 Энтропийные индексы представляют собой трансформацию индекса
Аткинсона, а параметр  может интерпретироваться как параметр «отвращения» к неравенству
(чем ниже , тем менее общество толерантно по отношению к неравенству). Коуэлл показывает,
что если параметр 1 и  = 1 - , энтропийные меры становятся эквивалентны мерам Аткинсона
(Cowell 1995).
3
Сен отмечает, что когда параметр   2, энтропийные индексы GE() приобретают «обратную
трансфертную чувствительность», что ставит под сомнение актуальность использования
энтропийных мер с параметром параметр   2 (Sen 1997).
2
4
Энтропийный индекс Тейла принимает значение в интервале (0; log) при yi
(0; ); второй индекс Тейла (среднее логарифмическое отклонение)
принимает значения в интервале (0; ), при yi (1; ). Коэффициент вариации
принимает значения в промежутке (0; (n – 1)/2).
Для сравнительной оценки влияния факторов на неравенство целесообразно
использовать среднее логарифмическое отклонение, GE(0), – вторую меру Тейла,
декомпозиция которой зависит от долей населения.
Среднее логарифмическое отклонение рассчитывается как:
GE(0) 

1
 ,
Ln

n i  yi 
где  – средние эквивалентные расходы; yi – расходы iой семьи; n – размер
выборки.
Метод статической декомпозиции энтропийных мер неравенства позволяет
оценить
структуру
неравенства
и
значимость
факторов
неравенства
в
определенный момент времени.
Если все семьи в выборочной совокупности разделить на j групп в
соответствии со значениями, которые принимает анализируемый признак (т.е., J =
1,2,3), то среднее логарифмическое отклонение раскладывается на компоненты,
отражающие неравенство между группами, и неравенство, существующее внутри
каждой из групп:
y 
GE(0)   j w j  GE(0) j   j w j Ln j  ,





inequality within
inequalitybetween
где внутригрупповое неравенство представляет собой сумму GE(0)j каждой из
групп J, взвешенных по их доле в общей структуре населения w j , а неравенство
между группами – это отношение средних расходов группы y j к среднему уровню
расходов по выборке .
Межгрупповая компонента неравенства интерпретируется как доля общего
неравенства, объясненная данным признаком, внутригрупповая компонента – как
доля общего неравенства, которая не объясняется данным признаком.
5
Помимо метода статической декомпозиции существует метод динамической
декомпозиции энтропийных индексов, который позволяет установить связь между
мерами неравенства для двух временных периодов t0 и t1:
GE(0)  GE(0)1  GE(0) 0
Формула
декомпозиции
изменений
общего
неравенства
для
среднего
логарифмического отклонения выглядит следующим образом:


 yj 
 yj 
GE(0)   w j GE(0) j  GE(0) j w j   Ln w j   w j  Ln   Ln( ~y j )  




j


j  j j  


TermA
TermC
 yj 
  w j Ln 

j  
TermB
Три компоненты изменений общего неравенства в правой части формулы
интерпретируются следующим образом:
- Компонента A: эффект от изменения внутригруппового неравенства. Когда
увеличивается
неравенство
внутри
одной
или
нескольких
групп
домохозяйств, увеличивается и общее неравенство, при условии, что
структура домохозяйств остается неизменной.
- Компонента
В:
эффект
от
изменения
неравенства
между
группами
домохозяйств. Если две группы домохозяйств имеют одинаковый уровень
внутригруппового неравенства, то увеличение разницы между средними
расходами этих групп приводит к росту общего неравенства, при условии,
что структура домохозяйств остается неизменной.
- Компонента С: эффект от изменения общей структуры домохозяйств, которое
происходит в результате изменений долей декомпозиционных групп в общей
структуре домохозяйств, при условии, что внутри- и межгрупповая
компоненты неравенства остаются неизменными.
Разделив обе стороны уравнения на значение GE(0)0, можно рассчитать, какое
значение каждый из этих эффектов оказал на изменение общего уровня
неравенства.
6