7 класс, геометрия
advertisement
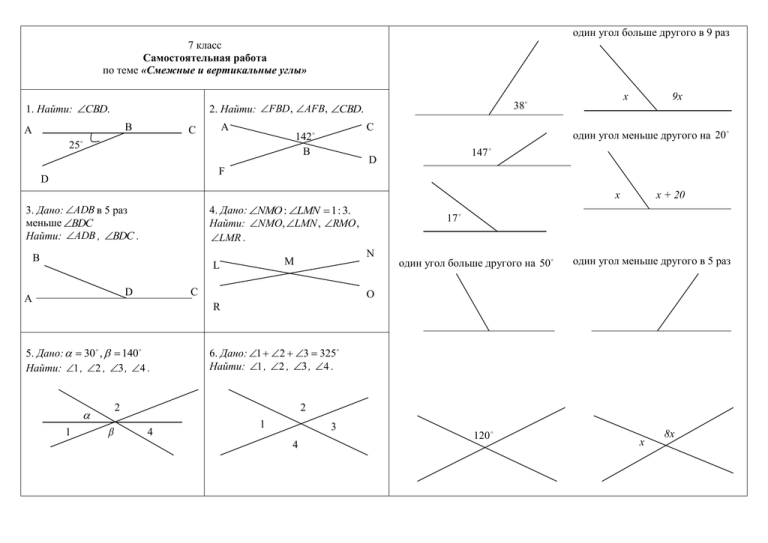
один угол больше другого в 9 раз 7 класс Самостоятельная работа по теме «Смежные и вертикальные углы» 1. Найти: СВD. В А 25 A С С 142 B х 38 2. Найти: FВD , AFВ, СВD. 9х один угол меньше другого на 20 147 D F D х 3. Дано: ADB в 5 раз меньше BDC Найти: ADB , BDC . 4. Дано: NMO : LMN 1 : 3. Найти: NMO, LMN , RMO , LMR . В С D А 17 N М L х + 20 один угол больше другого на 50 один угол меньше другого в 5 раз О R 5. Дано: 30 , 140 Найти: 1 , 2 , 3 , 4 . 2 1 6. Дано: 1 2 3 325 Найти: 1 , 2 , 3 , 4 . 2 4 1 3 4 120 х 8х 7 класс Контрольная работа по геометрии № 1 по теме «Основные свойства простейших геометрических фигур. Смежные и вертикальные углы» 1 вариант 7 класс Контрольная работа по геометрии № 1 по теме «Основные свойства простейших геометрических фигур. Смежные и вертикальные углы» 2 вариант 1. На луче с началом в точке А отмечены точки В и С. Найдите отрезок ВС, если АВ = 9,2 см, АС = 2,4 см. Какая из точек лежит между двумя другими? 1. На луче с началом в точке А отмечены точки В и С. Найдите отрезок ВС, если АВ = 3,8 см, АС = 5,6 см. Какая из точек лежит между двумя другими? 2. Один из углов, образовавшихся при пересечении 2. Один из углов, образовавшихся при пересечении двух прямых, в четыре раза меньше другого. двух прямых, на 70 больше другого. Найдите эти Найдите эти углы. углы. 3. Луч с – биссектриса ab . Луч d – биссектриса aс . Найдите bd , если ad 20 . 4*. В М О Дано: BOC 148 , OM OC , ОК – биссектриса COB . Найти: КОМ . 3. Луч с – биссектриса ab . Луч d – биссектриса aс . Найдите bd , если ab 80 . 4*. К С О А К М С Дано: АOК 154 , OК OC , ОМ – биссектриса КОА . Найти: СОМ . 7 класс Тестовая работа по геометрии по теме «Первый и второй признаки равенства треугольников» 1 вариант 1. В С N 7 класс Тестовая работа по геометрии по теме «Первый и второй признаки равенства треугольников» 2 вариант 1. В Е С М К А Для доказательства равенства треугольников АВС и MNK достаточно доказать, что: а) AC = MN; б) С N ; в) BC = NK. 2. D С F D F А Для доказательства равенства треугольников АВС и FED достаточно доказать, что: а) AC = FE; б) С Е; в) BC = ED. 2. К С М В А Е Для доказательства равенства треугольников АВС и EDF достаточно доказать, что: а) AC = FE; б) С Е; в) A F . 3. Чтобы доказать равенство равносторонних треугольников АВС и MNK достаточно доказать, что: а) А М ; б) AВ = MN; в) PABC PMNK . 4. Чтобы доказать равенство двух равнобедренных треугольников TOS и DEF с основаниями TS и DF соответственно, достаточно доказать, что: а) О Е; б) TS = DF и Т D ; в) TS = DF. 5. М С В N В А Для доказательства равенства треугольников АВС и MKN достаточно доказать, что: а) AC = MN; б) С N ; в) A M . 3. Чтобы доказать равенство равносторонних треугольников АВС и TSK достаточно доказать, что: а) А T ; б) AВ = TS; в) PABC PTSK . 4. Чтобы доказать равенство двух равнобедренных треугольников TOS и DEF с основаниями TS и DF соответственно, достаточно доказать, что: а) О Е; б) TS = DF и Т D ; в) TS = DF. 5. G С В N А Выберите верное утверждение: а) ВC = КМ; б) AВ = КN; К в) BC = NМ. L А Выберите верное утверждение: а) ВC = КG; б) AВ = КL; К в) BC = LG. 7 класс Теоретический тест по геометрии по теме «Треугольники» 1 вариант 1.Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 2. Если треугольник равносторонний, то: а) он равнобедренный; б) Все его углы равны; в) любая его высота является биссектрисой и медианой. 3. Если в двух треугольниках равны по две стороны и по одному углу, то эти треугольники равны. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 4. Биссектриса в равнобедренном треугольнике является его медианой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 5. Если в двух треугольниках равны по одной стороне и по два угла, то эти треугольники равны. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 6. В каком треугольнике только одна его высота делит треугольник на два равных треугольника? а) в любом; б) в равнобедренном; в) в равностороннем. 7. Оба треугольника равносторонние и имеют только по одной равной стороне. Равны ли эти треугольники? а) да; б) может быть да, а может нет; в) нет. 8. В каком треугольнике любая его высота делит треугольник на два равных треугольника? а) в любом; б) в равнобедренном; в) в равностороннем. 9. МКЕ ВСР , причем МКЕ - равнобедренный с основанием МК. Найдите величину В , если К 49 , Е 82 . а) 82 ; б) 49 ; в) другое число. 7 класс Теоретический тест по геометрии по теме «Треугольники» 2 вариант 1. Биссектриса в равнобедренном треугольнике является его медианой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 2. В каком треугольнике только одна его высота делит треугольник на два равных треугольника? а) в любом; б) в равнобедренном; в) в равностороннем. 3. Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 4. Если в двух треугольниках равны по две стороны и по одному углу, то эти треугольники равны. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 5. Если треугольник равносторонний, то: а) он равнобедренный; б) Все его углы равны; в) любая его высота является биссектрисой и медианой. 6. Если в двух треугольниках равны по одной стороне и по два угла, то эти треугольники равны. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 7. АВК ТМЕ , причем ТМЕ - равнобедренный с основанием ТМ. Найдите величину В , если Т 72 , Е 36 . а) 72 ; б) 36 ; в) другое число. 8. В каком треугольнике любая его высота делит треугольник на два равных треугольника? а) в любом; б) в равнобедренном; в) в равностороннем. 9. Оба треугольника равносторонние и имеют только по одной равной стороне. Равны ли эти треугольники? а) да; б) может быть да, а может нет; в) нет. 7 класс Контрольная работа по геометрии № 2 по теме «Треугольники» 1 вариант 1. На рисунке отрезки АВ и СД имеют общую середину О. Докажите, что ДАО СВО. 2. Луч АД – биссектриса угла А. на сторонах угла А отмечены точки В и С так, что АДВ АДС . Докажите, что АВ = АС. 3.Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС. 7 класс Контрольная работа по геометрии № 2 по теме «Треугольники» 2 вариант 1. На рисунке отрезки МЕ и РК точкой Д делятся пополам. Докажите, что КМД РЕД . 2. На сторонах угла Д отмечены точки М и К так, что ДМ = ДК. Точка Р лежит внутри угла Д и РК = РМ. Докажите, что луч ДР – биссектриса угла МДК. 3.Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А. 7 класс геометрия Тест на проверку теоретических знаний по теме «Признаки параллельности прямых» 1 вариант c a 1 8 6 3 5 7 b 2 1. Выберите верные утверждения: в) 7 и 6 - соответственные; е) 7 и 1 - накрест лежащие; 4 а) 1 и 3 - вертикальные; г) 5 и 3 - накрест лежащие; ж) 3 и 7 - односторонние. б) 5 и 1 - односторонние; д) 2 и 4 - смежные; 2. Выберите верные утверждения: Прямые a и b параллельны, если: а) 1 = 3 ; б) 8 + 5 = 180 ; в) 7 = 6 ; г) 8 + 3 = 180 ; д) 5 = 3 ; е) 2 = 6 ; ж) 1 + 4 = 180 ; з) 1 + 7 = 180 . 3. Указать продолжения высказывания, не соответствующие действительности. Прямые не параллельны, если при пересечении двух прямых секущей: а) сумма односторонних углов не равна 180 ; б) сумма соответственных углов равна 180 ; в) вертикальные углы не равны; г) накрест лежащие углы не равны; д) сумма смежных углов не равна 180 ; е) соответственные углы не равны. ___________________________________________________________________________________________________ 7 класс геометрия Тест на проверку теоретических знаний по теме «Признаки параллельности прямых» 2 вариант c а 2 5 7 8 3 b 1 1. Выберите верные утверждения: в) 7 и 6 - соответственные; е) 7 и 1 - накрест лежащие; 4 6 а) 1 и 3 - вертикальные; г) 5 и 3 - накрест лежащие; ж) 3 и 7 - односторонние. б) 5 и 1 - односторонние; д) 2 и 4 - смежные; 2. Выберите верные утверждения: Прямые a и b параллельны, если: а) 1 = 3 ; б) 8 + 5 = 180 ; в) 7 = 6 ; г) 8 + 3 = 180 ; д) 5 = 3 ; е) 2 = 6 ; ж) 1 + 4 = 180 ; з) 1 + 7 = 180 . 3. Указать продолжения высказывания, не соответствующие действительности. Прямые не параллельны, если при пересечении двух прямых секущей: а) сумма смежных углов не равна 180 ; б) накрест лежащие углы не равны; в) вертикальные углы не равны; г) сумма соответственных углов равна 180 ; д) сумма односторонних углов не равна 180 ; е) соответственные углы не равны. 7 класс геометрия Тест на проверку теоретических знаний по теме «Признаки параллельности прямых» 1 вариант d с а 1 5 b D B 2 6 3 4 Рис. 1 A 1. Рис. 1. Параллельны ли прямые a и b, если: а) 1 3; б) 1 4; в) 1 2 180 ; 2. Рис. 2. Дано: ABC CDE ; BC DE . с г) 5 6 90 ; E Рис. 2 д) 1 2. Доказать: AB CD. 7 класс геометрия Тест на проверку теоретических знаний по теме «Признаки параллельности прямых» 2 вариант d 5 3 B A b 6 C 1 C D а E 4 F 2 Рис. 1 Рис. 2 1. Рис. 1. Параллельны ли прямые a и b, если: а) 1 2 90 ; б) 3 4; в) 4 5; 2. Рис. 2. Дано: ABD ECF ; AD CF . д) 4 6 180 . г) 6 4; Доказать: AB EF . 7 класс геометрия Тест на проверку теоретических знаний по теме «Признаки параллельности прямых» 3 вариант B D A C B E Рис. 2 C 1. Рис. 1. Дано: AB BC ; A 60 ; CD биссектриса BCE. 2. Рис. 2. Дано: AB CD; BC AD. D A Рис. 1 Доказать: BC AD. Доказать: DC AB. 7 класс геометрия Тест на проверку теоретических знаний по теме «Аксиома параллельных прямых» 1. Выпишите лишние слова в скобках: Аксиома – это (очевидные, принятые, исходные) положения геометрии, не требующие (объяснений, доказательств, обоснований). 2. Выбрать окончание формулировки аксиомы параллельных прямых: Через точку, не лежащую на данной прямой, проходит: а) только одна прямая, параллельная данной; б) всегда проходит прямая, параллельная данной; в) только одна прямая, не пересекающаяся с данной. 3. Что может быть следствием аксиомы или теоремы? Указать неверные ответы. а) Утверждение, не требующее доказательства. б) Новая теорема, для доказательства которой использована аксиом или теорема. в) Утверждение, непосредственно выводимое из аксиомы или теоремы. 4. Указать следствия аксиомы параллельных прямых. а) Если отрезок или луч пересекает одну из параллельных прямых, то он пересекает и другую. б) Если две прямые параллельны третьей прямой, то они параллельны друг другу. в) Если прямая пересекает одну из параллельных прямых, то она пересекает и другую. г) Если три прямые параллельны, то любые две из них параллельны друг другу. д) Если две прямые не параллельны третьей прямой, то они не параллельны между собой. е) Если прямая пересекает одну из параллельных прямых, то она не может не пересекать другую. ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой. 5. Указать правильный ответ на вопрос. Если через точку, лежащую вне прямой, проведено несколько прямых, то сколько из них пересекаются с исходной прямой? а) Неизвестно, так как не сказано, сколько прямых проведено через точку. б) Все, кроме параллельной прямой. в) Все, которые имеют на рисунке точку пересечения с исходной прямой. 6. Почему, если одна из прямых, проходящих через точку, лежащую вне заданной прямой, параллельна этой прямой, то другие прямые, проходящие через эту точку, не могут быть ей параллельны? Указать неправильный ответ на этот вопрос. а) Это противоречит аксиоме параллельных прямых. б) Любая другая прямая, если она также параллельна заданной, совпадает с первой. в) Все другие прямые имеют точку пересечения с заданной прямой, хотя она может находиться на сколь угодно большом расстоянии от исходной точки. 7 класс Контрольная работа по геометрии № 3 по теме «Параллельные прямые» 1 вариант 1. Отрезки EF и PD пересекаются в их середине M. Докажите, что PE ║DF. 2. Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если CDE 68 . 7 класс Контрольная работа по геометрии № 3 по теме «Параллельные прямые» 2 вариант 1. Отрезки MN и EF пересекаются в их середине P. Докажите, что EN ║MF. 2. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, пересекающая сторону AB в точке E так, что AE = ED. Найдите углы треугольника AED если ВАС 64 . 7 класс геометрия Тест по теме «Сумма углов треугольника» 1 вариант 1. В треугольнике АВС A 90 , при этом другие два угла: А) один острый, другой может быть прямым или тупым; Б) оба острые; В) могут быть как острыми, так прямыми или тупыми. 7 класс геометрия Тест по теме «Сумма углов треугольника» 2 вариант 1. В треугольнике АВС B - тупой, при этом другие два угла могут быть: А) только острыми; Б) острыми и прямыми; В) острыми и тупыми. 2. В треугольнике АВС B - тупой, при этом другие два угла могут быть: А) только острыми; Б) острыми и прямыми; В) острыми и тупыми. 2. В треугольнике АВС A 90 , при этом другие два угла: А) один острый, другой может быть прямым или тупым; Б) оба острые; В) могут быть как острыми, так прямыми или тупыми. 3. В тупоугольном треугольнике могут быть: А) прямой и острый углы; Б) тупой и прямой углы; В) тупой и острый углы. 3. В остроугольном треугольнике могут быть: А) все углы острые; Б) один тупой угол; В) один прямой угол. 4. В остроугольном треугольнике могут быть: А) все углы острые; Б) один тупой угол; В) один прямой угол. 4. В тупоугольном треугольнике могут быть: А) прямой и острый углы; Б) тупой и прямой углы; В) тупой и острый углы. 5. В прямоугольном треугольнике могут быть: А) прямой и тупой углы; Б) два прямых угла; В) два острых угла. 5. В прямоугольном треугольнике могут быть: А) прямой и тупой углы; Б) два прямых угла; В) два острых угла. 7 класс 7 класс Домашняя контрольная работа по геометрии № 4 Домашняя контрольная работа по геометрии № 4 по теме «Соотношения между сторонами и углами треугольника» 1 вариант 1. На рисунке CÂM AÑF, PABC 34ñì , BC 12ñì . Найдите сторону АC треугольника АВС. Е по теме «Соотношения между сторонами и углами треугольника» 2 вариант 1. На рисунке EÀM ÄÂF , BC 17cì , PABC 45ñì . Найдите сторону АВ треугольника М АВС. Е М А В C А D В D C F F 2. В треугольнике MNK K 37 , M 69 , NP – биссектриса треугольника. Докажите, что MP < PK. 2. В треугольнике CDE E 76 , D 66 , EK биссектриса треугольника. Докажите, что KC > DK. 3. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найдите стороны треугольника. 3. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника. 7 класс Контрольная работа по геометрии № 4 по теме «Соотношения между сторонами и углами треугольника» 1 вариант 7 класс Контрольная работа по геометрии № 4 по теме «Соотношения между сторонами и углами треугольника» 2 вариант 1. В АВС АВ > BC > AC. Найдите А, В, С , если известно, что один из углов треугольника равен 120 , а другой 40 . 1. В АВС АВ < BC < AC. Найдите А, В, С , если известно, что один из углов треугольника прямой, а другой равен 30 . 2. В треугольнике АВС угол А равен 50 , а угол В в 12 раз меньше угла С. Найдите углы В и С. 2. В треугольнике АВС угол А равен 90 , а угол С на 40 больше угла В. Найдите углы В и С. 3. В треугольнике АВС угол С равен 90 , а угол В равен 35 , СD - высота. Найдите углы треугольника АСD. 3. В треугольнике АВС угол С равен 90 , а угол А равен 70 , СD - биссектриса. Найдите углы треугольника ВСD. 4. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найдите стороны треугольника. 4. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника. 7 класс геометрия Домашняя работа по теме «Прямоугольный треугольник» 1 вариант 1. 7 класс геометрия Домашняя работа по теме «Прямоугольный треугольник» 2 вариант 1. 60 A A 150 C B Найти острые углы треугольника АВС. 2. Высота остроугольного треугольника АВС образует со сторонами, выходящими из той же вершины, углы 46 и 18 . Найти острые углы треугольника АВС. 7 класс геометрия Домашняя работа по теме «Прямоугольный треугольник» 3 вариант 1. Дано : AD – биссектриса угла А А C B C Найти острые углы треугольника АВС. 2. Высота остроугольного треугольника АВС образует со сторонами, выходящими из той же вершины, углы 24 и 38 . Найти острые углы треугольника АВС. 7 класс геометрия Домашняя работа по теме «Прямоугольный треугольник» 4 вариант 1. Дано : AD – биссектриса угла А А D В Найти : острые углы треугольника АВС. 2. Биссектриса прямого угла прямоугольного треугольника образует с гипотенузой углы, один из которых равен 70 . Найдите острые углы этого треугольника. C D В Найти : острые углы треугольника АВС. 2. Высота прямоугольного треугольника, опущенная на гипотенузу, образует с одним из катетов угол 55 . Найдите углы этого треугольника. Теоретический зачет по теме «Соотношения между сторонами и углами треугольника» Вставьте в предложение пропущенные слова или закончите предложение. 1. Сумма углов треугольника равна….. 2. Внешний угол треугольника равен…. 3. В любом треугольнике либо все углы ….., либо два угла…., а третий ….. 4. Если все углы острые, то треугольник называется ….. 5. Сторона треугольника, лежащая против прямого угла называется….. 6. В треугольнике против большей стороны….. 7. Если один из углов тупой, то треугольник….. 8. Если два угла треугольника равны, то….. 9. Катет прямоугольного треугольника, лежащий против угла в 30 ,равен….. 10. Если один из углов прямой, то треугольник….. 11. Каждая сторона треугольника меньше….. 12. Каждая сторона треугольника больше….. 13. Сумма ….. прямоугольного треугольника равна 90 . 14. В треугольнике против меньшего угла….. 15. Если катет прямоугольного треугольника равен половине гипотенузы, то….. 7 класс Итоговый контрольный тест 1 вариант 7 класс Итоговый контрольный тест 2 вариант 1. Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами: â)36 ; à)24 ; á )30 ; ã)40 . 2. В прямоугольном треугольнике АВС Ñ 90 , À 30 , ÀÑ 10ñì , CD AB, DE AC. Найдите АЕ. а) 8 см; б) 6 см; в) 5 см; г) 7,5 см. 3. Прямые a и b параллельны, c – секущая. Разность двух углов, образованных этими прямыми, равна 130 . Найдите отношение большего из этих углов к меньшему. а) 3,8; б) 4,5; в) 6,2; г) 5,6. 4. Периметр равнобедренного треугольника равен 15 см, а одна из его сторон на 4 см меньше другой. Найдите сумму боковых сторон этого треугольника. 2 1 à )8 ñì ; á )6ñì ; â)6ñì или 11 ñì ; 3 3 1 ã)11 ñì . 3 5. Хорда АВ равна 18 см. ОА и ОВ – радиусы окружности, причем ÀÎÂ 90 . Найдите расстояние от точки О до хорды АВ. а) 13,5 см; б) 6 см; в) 9 см; г) 12 см. 6. В треугольнике МРК угол Р составляет 60% угла К, а угол М на 4 больше угла Р. Найдите угол Р. â)52 ; à)64 ; á )48 ; ã)56 . 7. В треугольнике АВС углы В и С относятся как 5 : 3, а угол А на 80 больше их разности. Найдите углы, на которые высота треугольника AD разбивает угол А. à)60 ,40 á )50 ,30 ; â)40 ,70 ; à)50 ,60. 8. Высоты равнобедренного треугольника, проведенные из вершин при основании, при пересечении образуют угол в 140 . Найдите угол, противолежащий основанию. â)40 ; à)70 ; á )100 ; ã)50. 9. Биссектриса угла при основании равнобедренного треугольника равна стороне треугольника. Определите угол при основании. â)60 ; à)45 ; á )36 ; ã)72. 10. На какое наибольшее число равнобедренных треугольников можно разделить данный равнобедренный треугольник тремя отрезками? а) 6; б) 4; в) 3; г) 2. 1. Величины смежных углов пропорциональны числам 4 и 11. Найдите разность между этими углами: â)96 ; à)84 ; á )76 ; ã)68. 2. В прямоугольном треугольнике АВС Ñ 90 , Â 30 , ÂÑ 18ñì , CÊ AB, ÊÌ ÂC. Найдите МВ. а) 9 см; б) 13,5 см; в) 12 см; г) 10 см. 3. Прямые m и n параллельны, c – секущая. Разность двух углов, образованных этими прямыми, равна 132 . Найдите отношение большего из этих углов к меньшему. а) 4,8; б) 5,8; в) 6,5; г) 6,2. 4. Периметр равнобедренного треугольника равен 22 см, а одна из его сторон на 5 см меньше другой. Найдите сумму боковых сторон этого треугольника. 1 1 à )11 ñì ; á )18ñì ; â)18ñì или 11 ñì ; ã)17ñì . 3 3 5. Расстояние от центра окружности О до хорды CD равно 13 см. ÑÎD 90 . Найдите хорды CD. а) 18 см; б) 13 см; в) 19,5 см; г) 26 см. 6. В треугольнике BDE угол B составляет 30% угла D, а угол E на 19 больше угла D. Найдите угол B. à)21 ; á )32 ; â)70 ; ã)51. 7. В треугольнике АВС угoл A на 50 больше угла В, а угол С составляет пятую часть их суммы. Найдите углы, которые образует биссектриса угла А со стороной ВС. à)70 ,110 á )80 ,100 ; â)60 ,120 ; à)90 ,90. 8. Высоты равнобедренного треугольника, проведенные из вершины при основании и из вершины, противолежащей основанию, при пересечении образуют угол в 140 . Найдите угол, противолежащий основанию. â)70 ; ã)110 . à)40 ; á )50 ; 9. Биссектриса угла при основании равнобедренного треугольника пересекает боковую сторону под углом, равным углу при основании. Определите угол при основании. â)45 ; à)72 ; á )36 ; ã)60. 10. На какое наибольшее число равносторонних треугольников можно разделить данный равносторонний треугольник тремя отрезками? а) 2; б) 6; в) 4; г) 3.