Материалы и контрольное задание №1 по математике для
advertisement
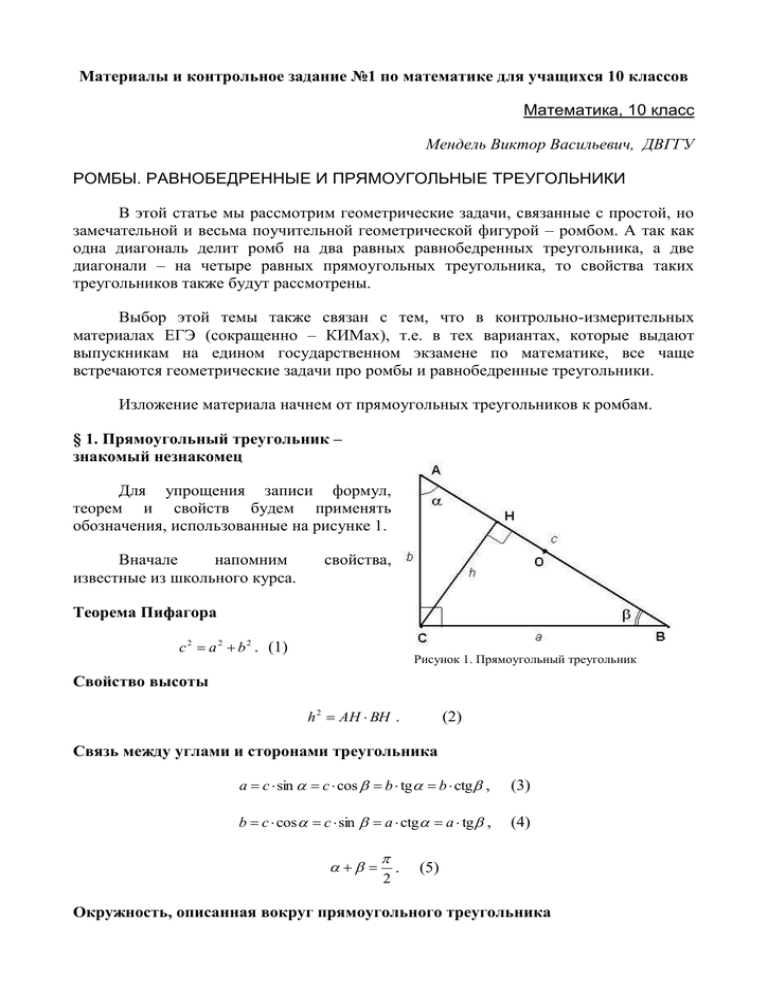
Материалы и контрольное задание №1 по математике для учащихся 10 классов Математика, 10 класс Мендель Виктор Васильевич, ДВГГУ РОМБЫ. РАВНОБЕДРЕННЫЕ И ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ В этой статье мы рассмотрим геометрические задачи, связанные с простой, но замечательной и весьма поучительной геометрической фигурой – ромбом. А так как одна диагональ делит ромб на два равных равнобедренных треугольника, а две диагонали – на четыре равных прямоугольных треугольника, то свойства таких треугольников также будут рассмотрены. Выбор этой темы также связан с тем, что в контрольно-измерительных материалах ЕГЭ (сокращенно – КИМах), т.е. в тех вариантах, которые выдают выпускникам на едином государственном экзамене по математике, все чаще встречаются геометрические задачи про ромбы и равнобедренные треугольники. Изложение материала начнем от прямоугольных треугольников к ромбам. § 1. Прямоугольный треугольник – знакомый незнакомец Для упрощения записи формул, теорем и свойств будем применять обозначения, использованные на рисунке 1. Вначале напомним известные из школьного курса. свойства, Теорема Пифагора c 2 a 2 b 2 . (1) Рисунок 1. Прямоугольный треугольник Свойство высоты h 2 AH BH . (2) Связь между углами и сторонами треугольника a c sin c cos b tg b ctg , (3) b c cos c sin a ctg a tg , (4) 2 . (5) Окружность, описанная вокруг прямоугольного треугольника Точка О - центр описанной окружности, является серединой гипотенузы. Радиус описанной окружности равен половине длины гипотенузы: R c . (6) 2 Окружность, вписанная прямоугольный треугольник в Рисунок 2. Прямоугольный треугольник и вписанная окружность Обозначим центр вписанной окружности буквой J, а радиус – r: 1 ab ch . (7) r (a b c) 2 ( a b c) ( a b c) Теперь получим еще несколько соотношений между различными элементами прямоугольного треугольника. Рассмотрим описанную вокруг прямоугольного треугольника окружность и точку H – основание высоты, проведенной к гипотенузе. Как известно, произведения отрезков секущих, проведенных через одну точку внутри окружности, равны. Именно из этого равенства получено соотношение (2): h 2 AH BH . Выразим в этом соотношении отрезки AH и BH через радиус описанной Рисунок 3. Медианы прямоугольного окружности и расстояние OH от основания треугольника. высоты до середины гипотенузы. Выполнив очевидные преобразования, получим h 2 R 2 OH 2 . (8) Рассмотрим теперь медианы прямоугольного треугольника. Выразим их длины через стороны треугольника. c 2 Очевидно, что mc R . (9) Две другие медианы легко выразить с помощью теоремы Пифагора: ma2 a2 b2 , 4 (10) Рисунок 4. Равнобедренный треугольник mb2 b2 a2 . 4 (11) Сложив формулы (10) и (11), с учетом (9) получим: 5mc2 ma2 mb2 . (12) §2. Равнобедренный треугольник Приведем основные соотношения между различными элементами равнобедренного треугольника (обозначения элементов приведены на рисунке 4). Выражение высоты 1 b 2 sin h b cos a ctg . 2 2 2 a (13) Радиус описанной окружности R a b . 2 sin 2 cos 2 (14) Радиус вписанной окружности r a a ah tgC ctg . 2 2 2 2b a (15) Площадь треугольника 1 1 S h a b 2 sin . 2 2 (16) Рисунок 5. Биссектриса Выражение основания через боковые стороны и угол (теорема косинусов) a 2 2b 2 (1 cos ) , a 2b sin 2 . (17) Биссектриса к боковой стороне AL b b2 AL . BL a ab Отсюда по теореме косинусов: CL2 b 2 b4 b3 2 cos . ( a b) ( a b) 2 (18) Выразив косинус из формулы (17) получим: CL2 b 2 b4 b3 2b 2 a 2 , 2 ( a b) 2 (a b) 2b 2 или после упрощений, b4 2b 3 a 2b a 2b(2b a) . CL b ( a b) ( a b) 2 a b2 2 2 (19) Медиана к боковой стороне 4mb2 2a 2 b 2 . (20) §3. Ромб Начнем с того, что условие перпендикулярности диагоналей не является достаточным признаком того, что выпуклый четырехугольник – ромб. Для того чтобы это условие стало достаточным, нужно потребовать, чтобы диагонали в точке пересечения делились пополам. Рисунок 6. Ромб и радиус вписанной окружности. С другой стороны, то, что диагонали одновременно служат биссектрисами углов выпуклого четырехугольника, является необходимым и достаточным признаком ромба. В ромб можно вписать окружность, но описать нельзя (за исключением того редкого случая, когда ромб является квадратом). Приведем некоторые вычислительные формулы для ромба. Площадь ромба S a 2 sin a h 1 AC BD 2a r . (21) 2 Диагонали (через сторону и угол) AC a tg 2 , BD a ctg 2 . (22) Радиус вписанной окружности (через сторону и угол) r a sin . 2 (23) Соотношение между диагоналями и сторонами AC 2 BD 2 4a 2 . (24) §4. Примеры решения задач Задача 1. Отрезок, соединяющий вершину тупого угла ромба с серединой противоположной стороны, делит этот угол в отношении 1:3, площадь ромба равна 8 3 , найдите стороны и углы. Решение. Поскольку данный отрезок поделил весь угол в отношении 1:3, то половину этого угла он делит пополам. Следовательно, треугольник, образованный двумя сторонами ромба и меньшей его диагональю будет равносторонним (все его медианы являются также и биссектрисами). Поэтому углы в ромбе 60 и 120 градусов. Далее, воспользовавшись формулой площади ромба (формула (21)), получим: a 2 sin 60 o 8 3 a 2 8 3 : Задача 2. Дан ромб острым углом 2. треугольники, диагоналями ромба, равных окружности. равна площадь вершинами которого этих окружностей. 3 16 a 4 . 2 со стороной a и В прямоугольные образованные вписаны четыре Определите, чему прямоугольника, являются центры Рисунок 7. Решение. Нетрудно показать (проделайте это самостоятельно), что центры указанных окружностей образуют квадрат со сторонами, равными удвоенному радиусу вписанных окружностей. Таким образом, задача сводится к вычислению радиусов этих окружностей. Сначала заметим, что катеты рассматриваемых прямоугольных треугольников равны половинам его диагоналей, а гипотенузы, боковым сторонам ромба. Выразим их с помощью формул (22): 1 1 AO a tg , BO a ctg , AB a . 2 2 Теперь вычислим радиус вписанной окружности прямоугольного треугольника (формула (7)): 1 1 1 r (a b c) AO BO AB a( tg ctg 1) . 2 2 4 Осталось вычислить площадь квадрата: S 4r 2 a2 ( tg ctg 1) 2 . 16 Задача 3. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 24 и 36 см. Найти катеты. Решение. Воспользуемся тем, что точки касания вписанной окружности прямоугольного треугольника и катетов, а также вершина прямого угла и центр вписанной окружности являются квадрата. Учитывая то, что отрезки касательных, проведенных из одной точки – равны, получим: a r 24, b r 36, c 60 . Применяя теорему Пифагора, получим уравнение: (r 24) 2 (r 36) 2 3600 . Решая его, найдем r 33 . Отсюда катеты равны 57 и 69 см. §5. Вопросы для самопроверки 1. Докажите, что следующие утверждения являются необходимыми и достаточными признаками равнобедренного треугольника: a. Две высоты треугольника равны; b. Высота проходит через центр описанной окружности; c. Центр вписанной окружности лежит на серединном перпендикуляре к одной из сторон. 2. Выше в статье упоминается о том, что перпендикулярность диагоналей не является достаточным признаком ромба. Приведите пример не ромба с перпендикулярными диагоналями. 3. Докажите формулу для медианы равнобедренного треугольника: 4mb2 2a 2 b 2 . 4. Выразите через стороны прямоугольного треугольника расстояние от точки пересечения медиан до катетов прямоугольного треугольника. 5. Выразите углы между биссектрисами равнобедренного треугольника через углы этого треугольника. 6. Докажите для высот прямоугольного треугольника соотношение 1 1 1 2 2. 2 ha hb hc Контрольное задание №1 Представленные ниже задачи являются контрольным заданием №1 для учащихся 10 классов. Решения необходимо оформить в отдельной тетради и выслать по адресу 680000, г. Хабаровск, ул. Дзержинского, 48, ХКЦТТ, ХКЗФМШ. Для зачета нужно набрать не менее 15 баллов (каждая правильно решенная задача оценивается в 3 балла). М.10.1.1. Гипотенуза прямоугольного треугольника делится точкой касания вписанной окружности на отрезки, отношение которых равно k (k > 1). Найти углы треугольника. (Указание: используйте метод из задачи 3 для выражения катетов через гипотенузу, а затем найдите углы.) М.10.1.2. Найти угол при основании равнобедренного треугольника, если известно, что его ортоцентр лежит на вписанной окружности. (Указание: ортоцентр – это точка пересечения высот треугольника. Нетрудно заметить, что расстояние от ортоцентра треугольника до его основания равно удвоенному радиусу вписанной окружности.) М.10.1.3. В прямоугольный треугольник вписана полуокружность так, что ее диаметр лежит на гипотенузе, а центр делит гипотенузу на отрезки 15 и 20 см. Найти радиус полуокружности. (Указание: центр рассматриваемой окружности лежит на пересечении биссектрисы прямого угла и гипотенузы. Опустите из этой точки перпендикуляры на катеты треугольника и исследуйте получившийся квадрат.) М.10.1.4. В прямоугольном треугольнике с катетами 18 и 24 см найти расстояние между центрами вписанной и описанной окружностей. (Указание: фактически нужно найти расстояние от точки пересечения биссектрис до середины гипотенузы. Удобно рассмотреть проекцию первой точки на гипотенузу. Она находится на расстоянии, от вершины прямого угла, равном радиусу вписанной окружности. На такое же расстоянии эта точка удалена от гипотенузы.) М.10.1.5. В равнобедренном треугольнике высота, проведенная к основанию, в 1,5 раза меньше радиуса описанной окружности. Найти угол при основании. (Указание: все необходимые формулы, выражающие высоту и радиус, даны в статье. Вам остается составить и решить тригонометрическое уравнение.) М.10.1.6. Доказать, что радиус окружности, касающейся гипотенузы и продолжений катетов прямоугольного треугольника, равен сумме длин гипотенузы и радиуса окружности, вписанной в треугольник. М.10.1.7. Острый угол ромба равен . Найдите отношение площади этого ромба к площади вписанной в него окружности. (Указание: как выразить радиус вписанной окружности через сторону и угол ромба вы найдете в статье.) М.10.1.8. Острый угол А ромба ABCD равен . Найти отношение радиуса окружности, вписанной в ромб, к радиусу окружности, вписанной в треугольник ABC. (Указание: выразите радиусы окружностей через сторону ромба и угол.) М.10.1.9. В ромб ABCD со стороной 4 см. и углом BAD, равным 600, вписана окружность. К ней проведена касательная, пересекающая AB в точке M и AD в точке P. Найти MB и PD, если MP=2 см. (Указание: используйте то, что длины отрезков касательных, проведенных к окружности из одной точки равны.)



