Контрольная работа № 1 Аналитическая геометрия Задание 1. Даны вершины треугольника А(х

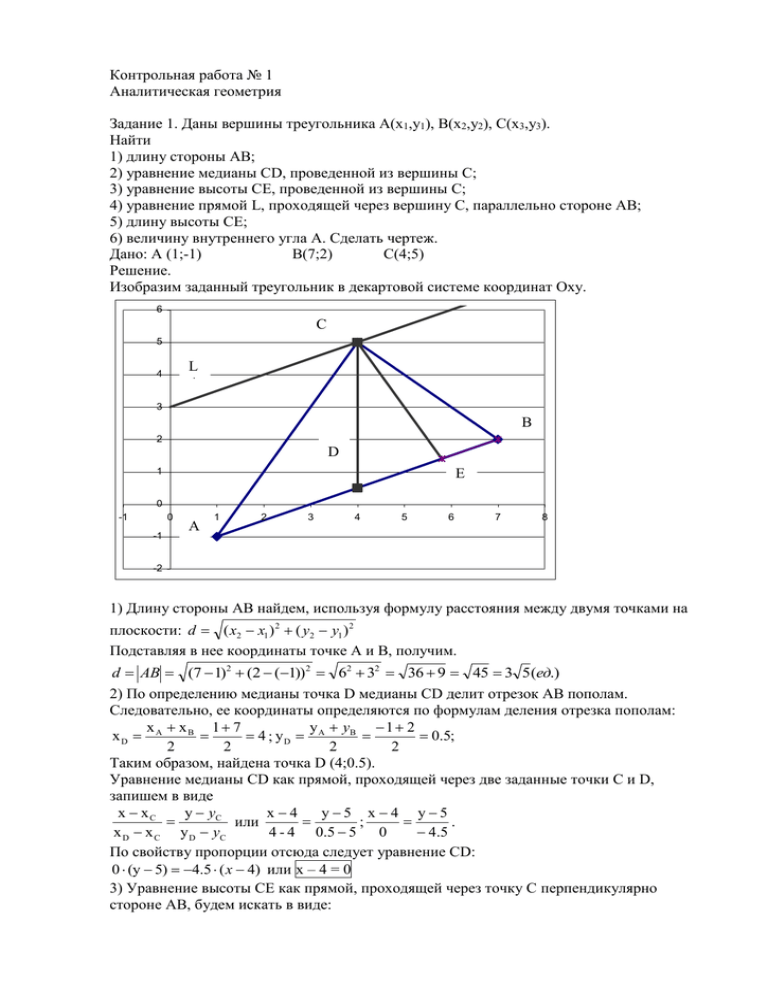
Контрольная работа № 1
Аналитическая геометрия
Задание 1. Даны вершины треугольника А(х1,y1), В(х2,y2), С(х3,y3).
Найти
1) длину стороны АВ;
2) уравнение медианы СD, проведенной из вершины С;
3) уравнение высоты СЕ, проведенной из вершины С;
4) уравнение прямой L, проходящей через вершину С, параллельно стороне АВ;
5) длину высоты СЕ;
6) величину внутреннего угла А. Сделать чертеж.
Дано: А (1;-1)
В(7;2)
С(4;5)
Решение.
Изобразим заданный треугольник в декартовой системе координат Оху.
6
C
5
L
A
4
3
B
2
D
1
E
0
-1
0
-1
A
1
2
3
4
5
6
7
8
-2
1) Длину стороны АВ найдем, используя формулу расстояния между двумя точками на
плоскости: d  ( x2  x1 ) 2  ( y2  y1 ) 2
Подставляя в нее координаты точке А и В, получим.
d  AB  (7  1)2  (2  (1)) 2  62  32  36  9  45  3 5 (ед.)
2) По определению медианы точка D медианы СD делит отрезок АВ пополам.
Следовательно, ее координаты определяются по формулам деления отрезка пополам:
x  xB 1  7
y  yB  1  2
xD  A

 4 ; yD  A

 0.5;
2
2
2
2
Таким образом, найдена точка D (4;0.5).
Уравнение медианы CD как прямой, проходящей через две заданные точки С и D,
запишем в виде
x  xС
y  yС
x4
y5 x 4 y5



или
;
.
4 - 4 0.5  5 0
 4.5
x D  x С y D  yС
По свойству пропорции отсюда следует уравнение СD:
0  (y  5)  4.5  ( x  4) или x – 4 = 0
3) Уравнение высоты СЕ как прямой, проходящей через точку С перпендикулярно
стороне АВ, будем искать в виде:
y  yc  KCE ( x  xc ) ,
где угловой коэффициент КСЕ, найдем из условия перпендикулярности прямых СЕ и АВ:
1
K CE  
.
K AB
Угловой коэффициент КАВ определим, используя формулу углового коэффициента
отрезка:
y  y A 2  (1) 3 1
K AB  B

  .
xB  x A
7 1
6 2
1
1

 2.
Следовательно, K CE  
K AB
12
Уравнение высоты, примет теперь вид
y – 5 = – 2 (x –4) ; y – 5 = – 2x + 8 или 2х + y – 13 = 0.
4) Аналогично, уравнение прямой L, проходящей через вершину С параллельно стороне
АВ, будем искать в виде
y  yc  K L ( x  xc ) ,
где угловой коэффициент КAB, найдем из условия параллельности прямых L и АВ:
1
K L  K AB 
2
Уравнение прямой L, примет теперь вид
y – 5 = 1/2 (x – 4); 2y – 10 = x – 4
или х – 2y +6 = 0.
5) Длину высоты СЕ найдем, используя формулу расстояния от точки С до прямой АВ
A x  B1 y1  C1
CE  1 1
,
A12  B12
где А1x+В1y+C1 = 0 есть общее уравнение стороны АВ:
1
y  yA  K AB ( x  xA ) или y  (1)  ( x  1),2 y  2  x  1 получим x – 2y – 3 = 0.
2
Подставляя в найденное уравнение координаты точки С, получим
1  4  2  5  3 4  10  3  9
9
9 5
CE 




(ед).
5
5
5
12  22
12  22
6) из рисунка видно, что внутренний угол А треугольника АВС есть угол, на который
нужно повернуть сторону АВ в положительном направлении (т.е. против часовой
стрелки) до совмещения ее со стороной АС. Поэтому тангенс угла А найдем по формуле:
K AC  K AB
tgA 
1  K AC  K AB
1
Угловой коэффициент K AB  (найден в п.3). Аналогично найдем
2
1
2
yC  y A 5  1 6
2  4  1  3  3 ; А  arctg 3
K AC 

  2. Следовательно tgA 
1 22 4 4
xC  x A 4  1 3
4
1 2
2
Ответ: 1) длина стороны AB  3 5 (ед.) ; 2) уравнение медианы СD: x – 4 = 0; 3) уравнение
высоты СЕ: 2х + y – 13 = 0 ; 4) уравнение прямой L: х – 2y – 3= 0; 5) длина высоты СЕ:
9 5
3
(ед) ; 6) величина внутреннего угла А А  arctg .
3
4
Задание 2. Составить уравнение и построить линию, для каждой точки которой
выполняется следующее условие:
1
Отношение расстояний до точки F (2;0) и прямой x  равно 2
2
Решение. Сделаем схематический чертеж по условию задачи:
3,00
x=0,5
M (x, y)
2,00
N(0,5;y)
1,00
F
0,00
0,00
-1,00
1,00
2,00
3,00
-1,00
1) Предположим, что произвольная точка плоскости М (х,y) лежит на линии. Тогда точка
N (0,5;y) является ее проекцией на прямой x = 0,5
2) по условию задачи выполняется следующее отношение расстояний:
FM
 2 или FM  2 NM
NM
3) используя формулу расстояния между двумя точками, выразим полученное буквенное
равенство в координатной форме и преобразуем его к виду канонического уравнения
одной из кривых второго порядка: окружности, эллипса, гиперболы или параболы.
( x  3) 2  ( y  0) 2  2 ( x  0.5) 2  x 2  6 x  9  y 2  4x 2  x  0.25 
 x2  6x  9  y 2  4x2  4x  1
y 2  3x 2  2 x  8  0  3x 2  2  3x 
2
1 
25

 3x 
  y2 
3
3

2
1
25

3 x    y 2 
3
3

1 1
25
  y2 
3
3 3
2
1

3 x  
y2
3


1
25
25
3
3
2
1

x 
y2
3


 1  гипербола
25
25
9
3
Это уравнение гиперболы, построим линию по ее уравнению.
5
4
3
2
1
0
-5
-4
-3
-2
-1 -1 0
-2
-3
-4
-5
Пересечение с осями
При у = 0
2
1

x 
3

 1;
25
9
2
1
25

x   
3
9

1
5
x 
3
3
4
6
x1  или x2    2
3
3
При х=0
y2

 1  решений нет.
25
3
Точка ( - 9/10; 0)
1
2
3
4
5
Задание 3. Даны точки А(х1,y1, z1), В(х2,y2,z2), С(х3,y3, z3).
Найти:
1) угол меду векторами AB и AC ;
2) уравнение плоскости P, проходящей через точку А перпендикулярно вектору AB ;
3) расстояние от точки С до плоскости Р;
4) уравнение прямой L, проходящей через точку В и С;
5) точку пересечения прямой L с плоскостью Р.
Сделать схематический чертеж.
Дано: А (-4;-2;0)
В(-1;-2;4)
С(3;-2;1)
Решение
Сделаем схематический чертеж.
B
C
M(x,y,z)
P
A
C’
D
1) Найдем векторы AB и AC , проходящие через 2 заданные точки:
AB  ( xB  x A ; y B  y A ; z B  z A )  (1  (4);2  (2);4  0)  (3;0;4)
AC  ( xC  x A ; yC  y A ; zC  z A )  (3  (4);2  (2);1  0)  (7;0;1)
Находим косинус угла между векторами по формуле:
AB  AC
3  7  0  0  4 1
21  4
25
1
cos  




25  50 5  5  2
2
AB  AC
32  02  42  7 2  02  12
 1 
0
Следовательно   arccos
  45
2


2) Пусть М (x;y;z) – произвольная точка плоскости Р. Тогда вектор
AM  ( x  x A ; y  y A ; z  z A )  ( x  4; y  2; z  0) будет перпендикулярен вектору AB .
Используя условие перпендикулярности двух векторов AB  AM  0 как равенство нулю
их скалярного произведения в координатной форме, получим общее уравнение плоскости
Р:
3  ( x  4)  0  ( y  2)  4  ( z  0)  0 или 3x  12  4z  16  0 или 3x  4z  12  0
3) Расстояние d от точки С до плоскости Р найдем по известной формуле:
A x  B1 y1  C1 z1  D1
d 1 1
,
A12  B12  C12
где А1x+В1y+C1z+ D1= 0 есть уже известное общее уравнение плоскости Р. Получим
3  3  0   2  4  1  12 9  4  12 25
d


 5(ед).
5
25
32  02  42
4) Уравнение прямой L, проходящей через две заданные точки В и С, имеют вид:
x 1 y  2 z  4
x 1
y2
z4
x  xB
y  yB
z  zB






или
или
.
4
0
3
3 1  2  2 1 4
xC  xB yC  yB zC  z B
5) Для нахождения точки D пересечения прямой L с плоскостью P, приравняем
отношения, входящие в уравнение прямой L, параметру t и получим параметрические
уравнения прямой L:
x 1
y2
z4
 t;
 t;
 t  x  1  4t; y  2  0; z  4  3t. 
4
0
3
x  4t  1; y  2; z  3t  4.
Подставляя значения x, y, z в общее уравнение плоскости P, получим значение параметра
t, при котором линия L пересекает плоскость P.
3  4t  1  4   3t  4  12  0  12t  12t  3  16  12  0  25  0
Отсюда следует, что точки пересечения D не существует:
Ответ
 1 
1) угол меду векторами AB и AC :   arccos
  450
 2
2) уравнение плоскости P : 3x  4z  12  0
3) расстояние от точки С до плоскости Р : d  5(ед).
x 1 y  2 z  4


4) уравнение прямой L:
.
4
0
3
5) точка пересечения прямой L с плоскостью Р: не существует.
.