1. 2. меньшего количества пачек бумаги хватит на 3 недели?
advertisement
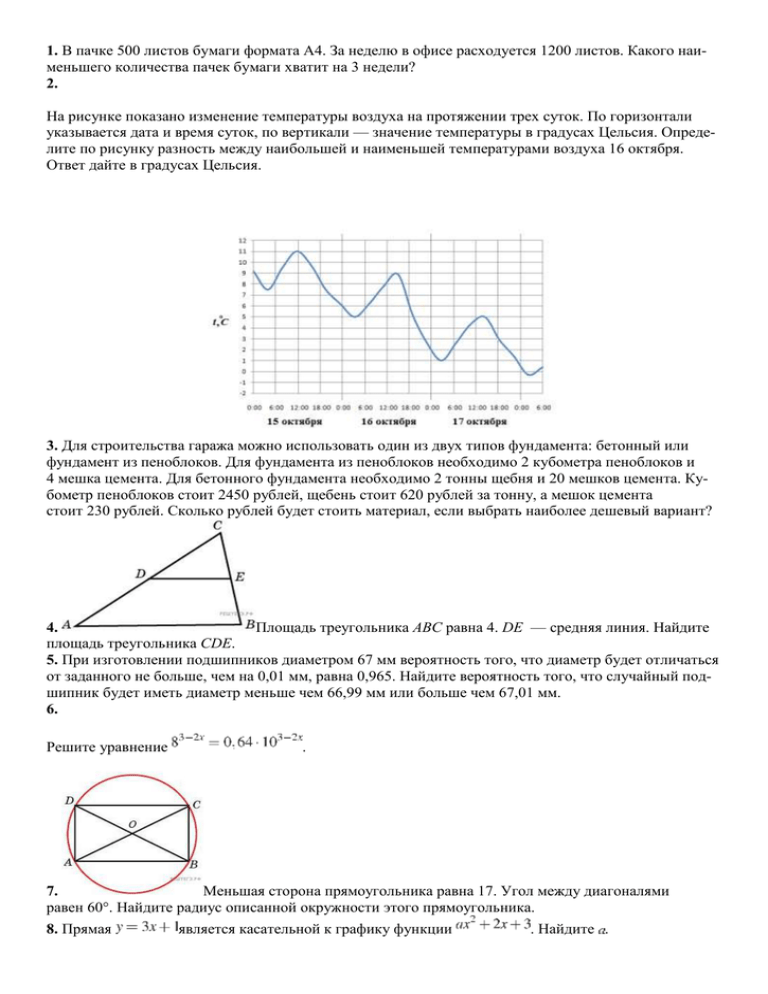
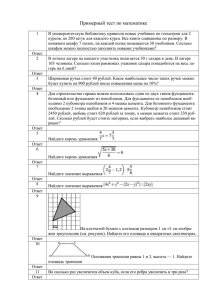
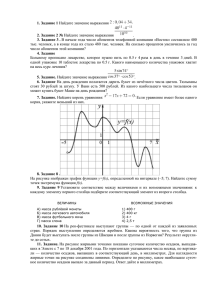
1. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какого наименьшего количества пачек бумаги хватит на 3 недели? 2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 16 октября. Ответ дайте в градусах Цельсия. 3. Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 2 кубометра пеноблоков и 4 мешка цемента. Для бетонного фундамента необходимо 2 тонны щебня и 20 мешков цемента. Кубометр пеноблоков стоит 2450 рублей, щебень стоит 620 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант? 4. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE. 5. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм. 6. Решите уравнение . 7. Меньшая сторона прямоугольника равна 17. Угол между диагоналями равен 60°. Найдите радиус описанной окружности этого прямоугольника. 8. Прямая является касательной к графику функции . Найдите . 9. =4, Найдите угол =4. Дайте ответ в градусах. прямоугольного параллелепипеда, для которого =5, 10. Найдите , если и . 11. Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле , где — частота вынуждающей силы (в ), — постоянный параметр, — резонансная частота. Найдите максимальную частоту , меньшую резонансной, для которой амплитуда колебаний превосходит величину не более чем на . Ответ выразите в . 12. В правильной треугольной пирамиде боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды. 13. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды? 14. Найдите точку максимума функции . 15. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку 16. В треугольной пирамиде MABC с основанием ABC ребро MA перпендикулярно плоскости основания, стороны основания равны 3, а ребро MB равно 5. На ребре AC находится точка D, на ребре AB точка E, а на ребре AM — точка L. Известно, что AD = 2 и BE = ML = 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L. 17. Решите неравенство: 18. Площадь трапеции ABCD равна 240. Диагонали пересекаются в точке O. Отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции втрое больше другого. 19. 31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк X рублей. Какой должна быть сумма X, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)? 20. При каких значениях а системы уравнении и равносильны? 21. На доске написано более 36, но менее 48 целых чисел. Среднее арифметическое этих чисел равно , среднее арифметическое всех положительных из них равно 6, а среднее арифметическое всех отрицательных из них равно . а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них?