проект- 10а

МОУ «Красногородская средняя школа»
проект подготовили:
учащиеся 10а класса
руководитель: учитель математики Самрова Г.В.
“Понятие функция такое же
основное и первоначальное ,как
и понятие множества.”
Хаусдорф Ф.
Основополагающий вопрос :
Какое место занимает тема
“Функция” в изучении школьного
курса алгебры ?
Типология проекта :
ознакомительно – ориентировочный
(информационный).
Категория учащихся : 9 – 11 классы.
Предметная область : математика.
Аннотация:
Начиная с 7 класса в центре внимания школьной математики
находится понятие функции. Однако по школьному
учебнику, количество часов, выделяемых на изучение темы
“ Функция” в разных классах , не позволяют показать в
полном объеме все многообразие задач , требующих для
своего решения функционального подхода , научить
учащихся глубоко понимать и использовать свойства
функции; нет времени излагать историю развития
возникновения понятия « функции» .
С другой стороны , авторы ЕГЭ уделяют много внимания
проверке определять по графику свойства функции,
использовать их в решении уравнений и неравенств.
Данный проект позволяет углубить знания учащихся по
истории возникновения понятия “функция” , по способам
задания функций , их свойствам и применению функций в
нестандартных ситуациях.
Образовательные цели:
- актуализация опорных знаний в
области математики ;
- умение применять теоретические
знания в нестандартных ситуациях .
Развивающие цели :
-
-
-
развитие интеллектуальных способностей
через исследовательскую деятельность ;
развитие умения самостоятельного поиска
необходимой информации ;
формирование умений анализировать ,
сравнивать , рассуждать , выделять
главное, ставить вопросы, видеть проблему .
Воспитательные цели :
-
-
воспитание трудолюбия ,
настойчивости в получении знаний ;
воспитание умения работать в
группе .
Этапы проекта :
1.Объявление темы проекта , выбор проблемы в
рамках темы проекта. (15.01.08)
2. Сбор информации по выбранной проблеме.
(16.01.08-22.01.08)
3. Анализ собранной информации , составление
плана работы. (23.01.08)
4.Исследовательская деятельность учащихся (при
помощи учителя). (23.01.08-1.02.08)
5.Оформление результатов работы : презентация ,
буклет , кроссворд. (2.02.08-10.02.08)
6.Защита работы.(16.02.08)
7.Подведение итогов.
Проблемные вопросы :
1.Рождение функции (презентация , кроссворд ).
руководитель группы : Сергеев Виталий.
2. Что можно узнать работая с графиком функции ?
(презентация , буклет ).
руководитель группы : Ильина Анастасия.
3. Простейшие преобразования графиков функций
(презентация ).
руководитель группы : Назаров Андрей.
4. Применение графиков функций к решению уравнений и
неравенств ( презентация , буклет ).
руководитель группы : Федорова Светлана.
5. По страницам материалов ЕГЭ ( презентация ).
руководитель группы : Фомченков Евгений.
МОУ «Красногородская
средняя школа»
ТЕМА: РОЖДЕНИЕ ФУНКЦИИ.
проект подготовили:
Сергеев В.
Скработун Д.
Ефимов В.
Петрова О.
руководитель: учитель математики
Самрова Г.В.
2008 год
«Под функцией переменяющегося
разумеют величину, которой
значение зависит от сего
переменяющегося»
Лобачевский Н.И.
Цель: изучить
историко-генетический подход к
понятию «функция»;
 понятие функции;
 способы задания функций;
 из чего и как конструируются
формулы.

Историко-генетический подход к понятию
«функция»





1.Пропедевтический период (с древнейших
времен до XVII
века).
2.Введение понятия функции через
механическое, геометрическое представления
(XVII век.)
3.Аналитическое определение функции (XVII
- нач.XIXв.)
4.Идея соответствия (XIXв.)
5.Дальнейшее развитие понятия функции
(XXв - ...).
1.Пропедевтический период (с
древнейших времен до XVII века).

вавилонские ученые (4-5тыс.лет назад) пусть
несознательно, установили, что площадь
круга является функцией от его радиуса
посредством нахождения грубо
приближенной формулы: S=3r2. Примерами
табличного задания функции могут служить
астрономические таблицы вавилонян,
древних греков и индийцев, а примерами
словесного задания функции - теорема о
постоянстве отношения площадей круга и
квадрата на его диаметре
2.Введение понятия функции через
механическое, геометрическое
представления (XVII век.)
Декарт Рене (15961650 гг.)
Французский философ, математик,
физик.
Разработана единая буквенная математическая символика,
которая вскоре получила всеобщее признание.
Аналитическое определение
функции (XVII - начало.XIXв)
Лейбниц Готфрид Вильгельм
(1646-1716 гг.)
Ввел термины “переменная” и
“константа”.
Бернулли Иоганн (1667-1748 гг.)
В 1718 году определил функцию
следующим образом: “функцией
переменной величины называют
количество, образованное каким
угодно способ из этой переменной
величины и постоянных”.
Аналитическое определение функции
(XVII - начало.XIXв.)
Эйлер Леонард (1707-1783 гг.) Даламбер Жан Лерон (1717-1783 гг.)
Эйлер (во “Введении в анализ бесконечного”): “Функция
переменного количества есть аналитическое выражение,
составленное каким-либо образом из этого количества и чисел
или постоянных количеств”.
Идея соответствия (19 век).
Лобачевский
Николай Иванович
(1792-1856 гг.)
Больцано Бернард
(1781-1848 гг.)
Дирихле Петер
(1805-1859 гг.)
В 1837 году немецкий математик П.Л. Дирихле так сформулировал общее
определение понятия функции: “y есть функция переменной x (на отрезке a  x
 b), если каждому значению x на этом отрезке соответствует совершенно
определенное значение y, причем безразлично каким образом установлено это
соответствие - аналитической формулой, графиком, таблицей либо даже просто
словами”.
Дальнейшее развитие понятия
функции (20 век - ...).
Н.М.Гюнтер
Советский математик Н.М.
Гюнтер опубликовал в 3040 годах нашего столетия
работы, в которых
неизвестными являются не
функции точки, а “функции
области”, что лучше
соответствует физической
сущности явлений.
Соболев Сергей Львович
(1908-1989гг.)
Прочитайте фамилии известных математиков,
внёсших свой вклад в формирование понятия
«функция», зашифрованные анаграммами:
1-НОТЮНЬ
2-ЛИДЕРИХ
3-ЛОЙБАСИКЧЕВ
4-ВШАЦР
5-РЕЙЛЭ
6-ЛУРБЕНЛИ
7-АРИКД
8-НТЮГРЕ
понятие функции
Переменная у называется функцией
переменной х, если:
-задано множество М численных
значений х;
-задан закон, по которому каждому
значению х из этого множества
соответствует единственное численное
значение у
Способы задания функций
«Установить соответствие и задать
функцию означает одно и то же»
Маркушевич А.И.



Аналитический
Табличный
Графический
Аналитический
элементарные функции






Постоянная (y=C, C=действительное число)
Степенная(y=xn)
Показательная(y=ax ,где a>0, не=1)
Логарифмическая(y=logax a>0, не=1)
Тригонометрическая(y=sinx, y=cosx, y=tgx,
y=ctgx)
Обратная Тригонометрическая(y=arctgx,
y=arcctgx)
Табличный

При табличном задании функции
составляется таблица, в которой указывается
ряд значений аргумента и соответствующих
значений функции(логарифмические
таблицы, таблицы значений
тригонометрических функций и.т.д.)
Y=x2
x
0
2
-2
5
y
0
4
4
25
Графический

При графическом задании даётся график
функции, и её значения, соответствующие
тем или иным значениям аргумента,
непосредственно находятся из этого
графика
Сложные функции:
аргумент является функцией
новой переменной
функция у = f (u), аргумент u является функцией
переменной х:
u = g (x)
Тогда переменная у также будет функцией х. Эта
функция называется сложной функцией или
функцией от функции. Она обозначается следующим
образом:
у = f [g (x)]
Сложные функции
Вывод
Функция- одно из основных математических и
общенаучных понятий, выражающее зависимость
между переменными величинами.
Каждая область знаний:
физика, химия, биология, социология,
лингвистика- имеет свои объекты изучения,
устанавливая свойства и взаимосвязи этих
объектов. Математика рассматривает
абстрактные переменные величины и в
отвлечённом виде изучает различные законы их
взаимосвязи, которые на математическом языке
называются функциями
кроссворд
10.
1.
2.
11.
9.
3.
8.
4.
5.
6.
7.
Вопросы:
1-График обратной пропорциональности
2-График линейной функции
3-Расположение графиков двух функций, если коэффициенты различны
4-Способ задания функций
5-Абцисса точки
6-Правило, которое принадлежит х и у некоторого множества чисел сопоставляет одно
определённое число у
7-Название функции у=кх+b
8-Плоскость, на которой выбрана система координат
9-Независимая переменная
10-Свойство линейной функции
11-Функция у=b, где b-некоторое число
Ответы на кроссворд











1-гипербола
2-прямая
3-пересекаются
4-табличный
5-координата
6-функция
7-линейная
8-координатная
9-аргумент
10-возрастает
11-постоянная
МОУ «Красногородская средняя общеобразовательная школа»
Тема:«Что можно узнать из графика
функции»
Работу выполнили:
Ильина Анастасия
Дмитриева Виктория
Петрова Мария
Смелова Алена
Руководитель: Самрова Г.В.
Красногородск,2008
Содержание
1. Что такое функция и график функции.
2. Свойства функции:
Возрастание / убывание функции
Чётность / нечётность функции
Непрерывность функции
Гладкость
Постоянство
Знакопостоянство
Выпуклость вверх / вниз
Периодичность
Ограниченность сверху / снизу
Асимптота
Монотонность
3. Характерные точки графиков:
Нули(корни) функции
Точка максимума
Точка минимума
Точка экстремума
Точка перегиба
Точка излома
Точка разрыва
4.
Обратные функции
5.
Д(f) Е(f).
Что такое функция и график функции?
Функцией называют отношение между
множествами X и У, при котором каждому
элементу множества Х соответствует элемент
из множества У.
График функции – множество точек на плоскости
с координатами
( х; f (x)) у = f(х)
Примеры графиков функций
На этом рисунке
показаны:
-Квадратичная функция
(Парабола)
-Обратная функция ( Гипербола)
- Линейная функция
Возрастание/убывание функции
Функция f (x) называется возрастающей на данном числовом
промежутке Х, если большему значению аргумента
х принадлежит Х соответствует большее значение функции
f (x),т.е. для любых х1, х2 из промежутка Х таких, что х2 > х1,
выполнено неравенство f (х2) > f (х1) .
Функция f (х) называется убывающей на данном промежутке
Х, если большему значению аргумента х принадлежит Х
соответствует меньшее значение функции f (х), т.е. для любых
х1, х2 из промежутка Х таких, что х2 >х1, выполнено
неравенство f (х2) < f (х1)
Примеры графиков.

Убывающая функция у =log х
1/2
Примеры графиков.

Возрастающая функция у =log2х
Чётность и нечётность функции
Функция f(х) называется чётной, если область её определения симметрична
относительно нуля и f(-х) = f(х) для любого х из области определения
функции f(х). Функция называется четной, когда она симметрична
относительно оси ординат(Оу)
Функция f(х) называется нечётной, если область её определения симметрична
относительно нуля и f(-х)=- f(х) для любого х из области определения
функции f(х). Функция называется нечётной, когда она симметрична
относительно начала координат.
Функции , не являющиеся ни чётными, ни нечётными, называются функциями
общего вида.
Непрерывность функции.
Непрерывность«сплошность»,
неразрывность
кривой,
изображающей
график,
возможность её
начертания без
отрыва
карандаша от
бумаги.
Гладкость функции.
Гладкость- плавность
кривой; график
поворачивает постепенно,
не имеет изломов и
заострений
Постоянство функции.
Постоянство
функциипараллельность
графика оси
абсцисс.
Знакопостоянство функции.
Знакопостоянство
функции- расположение
графика выше
(ниже) оси абсцисс.
Выпуклость вверх/вниз
Выпуклость вверх/вниз- любая
дуга графика лежит выше
(ниже) стягивающей её
хорды; касательной при
движении- точка касания по
графику слева направо
поворачивается по часовой
стрелке(против неё)
Периодичность функции.
Периодичность- график
можно разбить на
одинаковые по форме
участки, получаемые один
из другого сдвигом вдоль
оси абсцисс. (Аналитически
выражается наличием
такого числа Т>0, что f(х
+T)=f (x) для всех х)
Ограниченность (сверху) снизу.
Ограниченность(сверху) снизу- расположение графика всюду ниже
(выше) некоторой прямой, параллельной оси абсцисс.
(аналитически выражается наличием такого числа
М, что f (x)<М(f (x)>М) для всех х.
Асимптота функции.
Асимптота-это прямая, к
которой неограниченно
приближается точка,
движущаяся по графику,
неограниченно удаляясь от
начала координат.
Вертикальная асимптотапрямая х = b,где b- точка
«бесконечного разрыва»
графика, при смещении
аргумента и которой слева
или справа значения
функции неограниченно
возрастает по абсолютной
величине. При этом
график уходит
неограниченно ↑ или ↓
График функции log2(3-х),
вертикальная асимптота у =3
Асимптота функции.
Горизонтальная асимптотапрямая у = а, и которой
неограниченно
приближается график
при
х→+∞ (правая
асимптота) или при х→∞(левая асимптота)
х→+∞выражает процесс
неограниченного
увеличения х,
безграничное удаление
точки х вправо по оси
абсцисс; запись же х →∞ означает
неограниченное
удаление точки х влево
по оси абсцисс.
График функции у =4/х +1,
горизонтальная асимптота
у =1
Асимптота функции.
Наклонная асимптотапрямая
У= к х +b, к которой
график неограниченно
приближается при У= к х
+b (правая асимптота).
Аналитически наличие
асимптоты у = к х +b
обуславливается
возможностью
представления функции
в виде У= к х +b + 0(х),
где 0(х)→0
При х→ +∞ или х→ -∞
график
Монотонность функции.
Функция у = f (x) называется монотонно возрастающей на
данном множестве Х, если для любых х1; х2 принадлежит
Х, х1<х2 следовательно f (x1) < f (x2), т.е. большему
значению аргумента соответствует большее значение
функции. Функция у < f (x) называется монотонно
убывающей на данном множестве Х, если для любых х1;
х2 принадлежит Х, х1<х2 следовательно f (x1) > f (x2), т.е.
большему значению аргумента соответствует меньшее
значение функции.
Нули функции.
Нули(корни)
функции- точки,
которых график
достигает оси ох.
Аналитическирешение уравнения
f (x)=0.
Точка максимума.
Точка максимумаабсцисса «вершина
графика», точка, в
которой функция
определена и в
которой возрастание
функции сменится
её убыванием.
Точка А-точка
максимума
Точка минимума.
Точка минимумаабсцисса
«дна впадины» на
графике, точка, в
которой функция
определена её
убывание изменится
на возрастание.
Точка В-точка
минимума.
Точка экстремума.


Точкой экстремума
графика называют
точку максимума или
минимума данного
графика.
Точки Q и L-точки
экстремума.
Точка перегиба.
Точка перегиба- это
точка графика, при
переходе через
которую меняется
направление его
выпуклости.
Точка излома.
Точка излома- точка
графика, в которой
резко, скачком меняется
направления движения
по графику.
Точки А,С и L- точки
излома.
Точка разрыва.
Точка разрыва- точка на оси
абсцисс, при прохождении
на или под которой график
терпит разрыв и для его
продолжения необходимо
оторвать карандаш от
бумаги. К точке разрыва
причисляются также те
концы области определения
функции, в которых она не
определена.
Обратные функции
Если каждому х принадлежащему D(f) соответствует единственный у
принадлежащему Е(f) и обратно- каждое значение у
принадлежащему Е(f) соответствует единственному х
принадлежащему D(f), то в этом случае можно построить новую
функцию, определённую на Е(f) и такую, что каждому у
принадлежащему Е(f) ставится в соответствии х
принадлежащий D(f), удовлетворяющий уравнение у = f (x).
Заметим, что если функция у = f x) монотонна в своей области
определения D(f),то она всегда имеет обратную. Для
нахождения функции, обратной данной у = f (x) надо выразить
через у:g(у), а затем записать полученную функцию в обще принятой
формуле у = g(у).
Отметим, что если функции у = f (x) и у = g(у) являются
взаимообратными, то область определения функции f совпадает с
множеством значений функции g, т.е. D(f)= Е(g) и наоборот,
т.е. D(g) = Е(f).
Графики взаимно обратных функций симметричны
относительно прямой у = х
Взаимно обратные функции:
у = хn
y = sin х
y = cos x
y =tg x
y =ctg x
y =lognс
и
и
и
и
и
и
у =n√¯ х
у =arcsin x
у =arccos x
у =arctg x
у =arcctg x
у = сⁿ
Обратные функции.

Обратные функции
х
у =log2х и у =2
Обратные функции.

Обратные функции
2
у=х иу=
√¯х
Множество значений функции. Область
определения функции.


E (f)- множество значений зависимой
переменной.(множество значений функции.)
D (f)-множество значений независимой
переменной при которых функция
определена.(Область определения функции.)
Вывод:


График функции наиболее доступно и
наглядно отражает особенности
изучаемой зависимости.
Функция: просто, сложно, интересно.
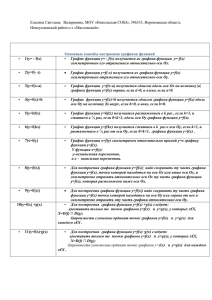
График функции y= f(ax) получается
сжатием графика функции y= f(x) вдоль 1
_
оси Ох в а раз при а>1 или растяжением в а
раз при 0<a<1. График функции y= f(-ax),
а>0 получается симметрично путём
отражения графика функции y= f(ax)
относительно оси Оу.
График функции y= f(x+b) получается
сдвигом графика функций y= f(x)
вдоль оси Ох на –b, т.е. сдвиг
производится вправо, если b<0, и влево,
если b>0.
y  x2
y  ( x  6) 2
График функции y= Af(x) получается
растяжением графика функции y= f(x)
вдоль оси Оу в А раз при А>1 или
1
сжатием в __
раз при 0<A<1. График
А
функции y= -Af(x), A>0 получается
симметричным отражением графика
функции y= -Af(x) относительно оси Ох
y  0,5x 2
y  0,5 x 2
y  x2
График функции y= f(x)+b получается
сдвигом графика функции y= f(x) вдоль
оси Оу на b вверх при b>0, вниз при b<0.
y=x
y=x-5
х -х
Y= _____
3 3 _ 2
Выполним почленное деление,
тогда:
Х
У1= 0.5*3
-Х
У2= -0.5*3
X
Y=
0.5*3
1
-X
Y2= -0.5*3
X -X
Y=______
3 -3
2
2
Y= x(x – 1)
2
Y2= x -1
Y 1= x
2
2
Y= x(x -1)
Y= ___
x
2
x -1
2
Y2= x -1
Y 1= x
x
y 2
x 1
Вывод:
1.Назаров Андрей 10 «а»
2.Ефимов Юрий 10 «а»
3.Лукина Олеся 10 «а»
4.Владимиров Иван 10 «а»
5.Иванов Артём 10 «а»
МОУ «Красногородская
средняя общеобразовательная школа»
Работу выполнили:
рук. группы Фёдорова Светлана
1. Евдокимова Юлиана
2. Корнеева Ирина
3. Тюркина Анна
Руководитель: Самрова Г. В.
Цель: Выяснить, как применяются
графики в решении
неравенств;
 уравнений;
 систем уравнений;
 уравнений с параметрами;
 заданий на применение свойств функции.

Неравенства.
3|x| - 2 < 2 – x
у1 = 3|x| - 2
у2 = 2 – x
Ответ: х ε (-2; 1)
Уравнения.
|5-|x|| = 3
у1 =|5-|x|
у2 = 3
Ответ: х1=-8; х2=-2; х3=2; х4=8.
Уравнения.
xlog2(x+1) = log1/3x + 7
у1 = xlog2(x+1)
у2 = log1/3x+7
Ответ: х = 3.
Системы уравнений.
log2(x-5) = y - 1
y + |x-5| - 4 = 0
{
у1 = log2(x-5) + 1
у2 = 4 - |x-5|
Ответ: х = 7
Системы уравнений.
Пусть (х0; у0) – решение системы
Найти: х0 + у0
y – 3 = |x-2|
x+1
y=2
{
у1 = |x-2|+ 3
у2 = 2x+1
х0 + у 0 = 1 + 4 = 5
Ответ: 5
Уравнения с параметрами.
При каких значениях параметра а число
корней уравнения ||x²-2x|-7| = a в четыре
раза больше а?
y1 = ||x²-2x|-7|
y2 = a
Ответ: а = 1
Неравенства с параметрами.
При всех значениях параметра а решите
неравенство ах > 1/х
а>0
a≤0
у1 = 1/х
у2 = ах
x ε (-1/√a; 0) υ (1/√a; +∞)
x ε (- ∞; 0)
Свойства функции.
Найти наименьшее значение функции f (x).
f (х) = log1/4(60+4x-x2)
1) квадратичная функция
у = 60 + 4x - x2
а =- 1<0, ветви параболы направлены вниз;
(х0; у0) вершины = (2; 64)
хмах = х0 = 2 =>
2) для логарифмической
функции минимальное значение
х=2
f (х) = log1/4(60+8-4) = - 3
Ответ: - 3
Свойства функции.
y = log3(3+|x|) - 5x/|x|,
Найти: Е(у)
log3(3+x) - 5, x > 0, x ≤ 6
{log (3-x) + 5, x < 0
у=
3
Ответ:
Е(у) = (-4;-3] υ (6;+∞)
х≤6
Вывод:

построение графиков функций -один из
способов решения задач, удобен при
решении нестандартных заданий.
МОУ «Красногородская средняя
общеобразовательная школа»
Тема «По страницам материалов ЕГЭ»
«Математику нельзя изучать, наблюдая,
как это делает сосед.» Нивен А.
Выполнили: учащиеся 10«А»:
Годунова Наталья
Дмитриев Михаил
Николаева Ирина
Полубан Алла
Ушкачев Павел
Фомченков Евгений.
Руководитель:учитель математики
Самрова Г.В.
р.п. Красногородск
2008 г.



Цель исследования:
Анализ работ ЕГЭ за 2003-2007 год
Выяснить на сколько широко
представлен раздел “ Функции” в
работах экзамена.
Функции их свойства и
графики
2003 год-40%
2007 год-38%
Группа
Уровень
сложности
Планируемая
Трудность
заданий в %
A
Базовый
60-70
B
Повышенный
25-40
C
Высокий
5-8
Неизменные задания ЕГЭ по
математике





распознавание графиков функций.
нахождение производной функции.
варианты заданий, связанных с ОДЗ
функции.
варианты заданий, связанных с
множеством значений функции.
решение заданий, которые связаны с
нахождением max и min функции.
Изменения заданий ЕГЭ по математике
(переход заданий из части «A» в часть «B»)


проверка геометрического смысла
производной (усложненные варианты,
связанные с угловым коэффициентом
(перешло в группу «B» с 2004 г)
задания, связанные с нахождением max
или min функции, сочетались в группах
«A» и «B».
Демонстрационный
вариант ЕГЭ по математике
2008
г.
А4.Указать график чётной функции (выбрать вариант, в
котором график симметричен oy)
А5.Найти производную функции
y  x 6  4 sin x
5
y

6
x
 4 cos x значений функции y=1,5+log x
A6.Найти множество
1,5
(-∞;+∞)
A7.На рисунке изображены графики y=f(x) и y=g(x),
заданных на промежутке [-3;6] найти x, для которых
f(x)≥g(x)
A10.Найти область определения функции
x
y

1
/
3
 1 / 27
т.к. 5-4x≤3 a=1/3<1=>x≥0,5 x принадлежит [0,5;+∞)


B5.Прямая, проходящая через начало координат,
является касательной к графику y=f(x) в A(-7;14),
найти f´(-7)
решение: A(x;f(x))=> y=-2x y´=(-2x)´=-2
B8.Функция y=f(x) определена на всей числовой
прямой и является чётной периодической
функцией с периодом, равным 6.На отрезке [0;3]
функция задана формулой 1)f(x)=2+2x+x² xв=b/2a xв=1 yв=3
2)т.к. четная функция, то эта часть симметрична
относительно oy.
3)в точках периода (-3) и (3) сделать симметрию
относительно x=3
C-1Найти наибольшее значение функции
2
2
3
2
f ( x)  1  x  2  1  x  x  3x
Р:1)Найду область определения
функции 1-x²≥0 x1=1 x2=-1 x
принадлежит [-1;1]
2)Наибольшее значение допускается
при x=0 =>f(0)=( 1 0 -2)+ 1 0+0-3-0=(-1)=1+0+0=1+1=2
Ответ: y max=2
C-3.Найти все значения a, для которых при любых x из промежутка
(-3;1]
значение выражения x-8x²-2 не равно значению выражения ax²
4
Р:1)рассмотрю функции:y=x-8x²-2
y´=4³-16x=0 4x(x-2)(x+2)=0 x1=0
x2=2 x3=-2
ymin(-2)=16-32-2=-18
ymin(2)=16-32-2=-18
yminx(0)=-2 y(-3)=-81-72-2≠7
y(-1)=1-8-2=-9
2)y=ax²-парабола а>0 ветви вверх a<0 ветви вниз
3)исследую графически
а) при каких a<0 y=-9 при x (-9;1] при x=-1 и
а=-9 y=-9 => a<-9, т.е.
a (-∞;-9)
б)при каких a>0 y=7, если x=-3 и a=7/9=>
а [7/9;+∞)
Ответ: a (-∞;-9) с объединением [7/9;+∞)
Решать или думать
1)y=log0,5(2x-x²)
a) (0;2)
б) (-∞;2) с объединением (2;+∞)
в)[0;+∞) г) (-∞;0) c объединением [2;+∞)
2) y  4 5  log 0.5 2 x
а) (0;2]
б) (0;5/4]
в) (0;5]
г) (0;16]
3) y  5  log 2 2 x
а) (0;2]
б) (0;2,5]
в) (0;5]
г) (0;16)
4) y  4 1  7 x * 49 x
а) [-2;0]
б) (0;2]
в) (-∞;-2) c объединением
[2;+∞]
г) (-2;2]
Способы контрольных точек, граничных точек.
2
Вывод
1)Необходимо четко знать основные свойства
каждого вида функции.
2)Полезно знать простейшие преобразования
графиков функций
3)При построении графика функции должны
быть отмечены основные его особенности
4)Для исследования более сложных
функций и построения графиков этих
функций необходимо использовать
производную функции.
Литература:
1)Гельфанд И.М. Глаголева Е.Г., Шноль Э.Э.«Функции и графики»М: Наука, 1968-96 с
2)Касаткин Г.В., Шевченко Л.В. «Готовимся в ВУЗ. Задачи и тексты
по математике»-М: Дрофа, 2004-224с
3)Ковалева Г.И., Бузулина Т.И. ,Безрукова О.Л., Розка Ю.А.
«Математика Тренировочные тематические задания» М:
«Учитель» 2005-271 с.
4)Рязановский А.Р. «Алгебра и начала анализа: 500 способов и
методов решения задач по математике для школьников и
поступающих в вузы.- М: Дрофа, 2001-480 с.
5)Шарынин И.Ф. «Факультативный курс математике: Решение
задач-М: Просвещение, 1989-252 с.
Анкета.
1.Какая тема исследования тебе понравилась больше всего?
2.У какой группы на твой взгляд лучшая презентация? Лучшее
выступление?
3. Показал ли ты свои знания на уроке ?
4. Понравился ли ты себе на уроке ?
5.Ты повысил свои знания ?
6.Лучший на твой взгляд момент на уроке?
7.Твоё мнение о проведённом уроке?