Описательная статистика Часть 2 ЛЕКЦИЯ 3

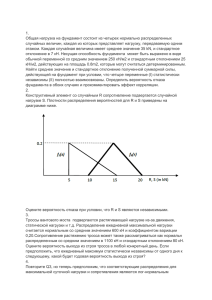
ЛЕКЦИЯ 3
по курсу «Математические методы в инновационной и управленческой
деятельности»
Описательная
статистика
Часть 2
СТАТИСТИКИ ЧИСЛОВЫХ ХАРАКТЕРИСТИК
ОДНОГО ИЗМЕРИМОГО ПРИЗНАКА
СРЕДНИЕ ЗНАЧЕНИЯ
• В качестве характеристик измеримого признака вместо
исходных значений величин или таблицы их частот
используются числовые характеристики, называемые
также статистическими мерами, которые служат для
описания и сравнения распределений.
• Важнейшей и чаще всего применяемой на практике
статистической характеристикой является среднее
значение, описывающее одним числом результаты
некоторого ряда измерений.
• Для статистических исследований в технике особый
интерес представляют следующие средние значения:
среднее арифметическое, медиана, или срединное
значение, модаD.
Среднее арифметическое, Х
• Например, на предприятии рассчитывается
среднемесячная доля брака, средний расход сырья в цехе
или среднесуточная производительность агрегата; при
метеорологических исследованиях вычисляют
среднегодовую температуру или среднесуточную
влажность воздуха.
• Среднее арифметическое ряда измерений объема n со
значениями x1, х2,...,хn значения определяется по формуле
1
1 n
x  ( x1  x2  ...  xn )   xi
n
n i 1
(суммирование индивидуальных значений и деление суммы
на количество величин)
ВЫБОРОЧНОЕ СРЕДНЕЕ
• Для выборки, состоящей из чисел Х„ Хг, Хп, выборочное среднее
(обозначаемое символом X ) равно
Свойства среднего арифметического
• Среднее арифметическое зависит от всех
элементов выборки
• Наличие экстремальных значений значительно
влияет на результат
• Среднее арифметическое может исказить смысл
числовых данных.
• Описывая набор данных, содержащий
экстремальные значения, необходимо указывать
медиану либо среднее арифметическое и медиану
Медиана (срединное значение), Ме
• Для ее вычисления все наблюдения необходимо
расположить в порядке возрастания или убывания
результатов измерений.
• Если n — нечетное число, то медиана - число,
находящимся в середине упорядоченной
последовательности.
• При четном n медиана равна среднему арифметическому
двух расположенных в середине значений упорядоченной
последовательности.
• ПРИМЕР
• Чтобы вычислить медиану выборки, сначала необходимо упорядочить
исходные данные.
• В соответствии с правилом, относящимся к выборкам, содержащим
нечетное количество элементов, позиция медианы вычисляется по
формуле
• Таким образом, медиана равна 6,5.
• Обратите внимание на то, что медиана, равная 6,5, ненамного больше
среднего значения, равного 6,08.
• ПРИМЕР
• Упорядоченный массив теперь выглядит так .
Согласно правилу, относящемуся к вычислению медианы выборки,
содержащей четное количество элементов, позиция медианы задается
формулой
Следовательно, медиана равна среднему значению, вычисленному по
третьему и четвертому элементам, т.е. 12,2.
Свойства медианы
• Медиана зависит от одного или двух срединных
значений ряда измерений
• Остальные значения последовательности можно
произвольно варьировать, не изменяя при этом медиану, в
то время как среднее арифметическое может существенно
измениться
• Особенно легко найти медиану малого количества
измерений
• Медиана используется для построения контрольных карт,
где ей отдается предпочтение перед средним
арифметическим, в выборках измерений из 5 или 7
значений
Мода D
•Мода D (наиболее вероятное значение) есть наиболее
часто встречающаяся в данном ряде измерений величина.
•Для дискретной случайной величины X D можно
установить непосредственно по таблице частот как
значение признака, имеющее максимальную абсолютную
частоту.
•Для непрерывной случайной величины Х моду D
определяют при наличии первичной таблицы
распределения как значение с максимальной абсолютной
частотой или (при отсутствии такой таблицы)
приближенно по таблице частот.
Мода D
•Если имеется только таблица частот, т. е. сгруппированный
материал, то можно определить лишь интервал, в который
попадает мода D - интервал с наибольшей абсолютной
частотой hm.
•При графическом представлении эмпирического
распределения в виде полигона частот D равна значению
измеримого признака, которому соответствует максимум
ординаты полигона.
•Многовершинные распределения частот (с несколькими
максимумами) обладают несколькими модами, поэтому для
их характеристики удобнее избрать моду D, а не среднее
арифметическое, так как она лучше отражает типичные
черты распределения, чем среднее значение или медиана
• ПРИМЕР
• Системный администратор подсчитывает количество сбоев сервера,
происходящих за день
• Данные его наблюдений за последние две недели
• Вычислите моду этой выборки .
• РЕШЕНИЕ. Упорядочим массив.
• Чаще всего в этой выборке повторяется число 3, следовательно, мода
равна 3
• Т. о. можно утверждать, что сервер сбоит, как правило, 3 раза в день
• Мода этой выборки равна 3, а выборочное среднее равно 4,5
• Число 26 является выбросом, поэтому для оценки среднего
количества сбоев за день следует пользоваться медианой или модой, а
не средним арифметическим значением.
Квартили
• Квартили (quartiles) — это показатели, которые чаще всего
используются для оценки распределения данных при описании
свойств больших числовых выборок.
• В то время как медиана разделяет упорядоченный массив пополам
(50% элементов массива меньше медианы и 50% — больше), квартили
разбивают упорядоченный набор данных на четыре части.
• Квартили вычисляются по формулам
• Первый квартиль Q1 — это число, разделяющее выборку на две части:
25% элементов меньше, а 75% — больше первого квартиля.
Третий квартиль Q3 — это число, разделяющее выборку на две части:
75% элементов меньше, а 25% — больше третьего квартиля.
• ПРИМЕР
• Вычислим квартили выборки. Упорядоченный массив имеет следующий вид.
• Это означает, что 25% значений СВ не превышает -0,7%.
Среднее геометрическое
• В отличие от среднего арифметического среднее геометрическое
позволяет оценить степень изменения переменной с течением
времени.
• Среднее геометрическое ряда измерений объема n с членами х1,
х2, …, xn определяется формулой
x  n x1  x2 ...xn
Вариация числовых данных
• Важное свойство числовых данных — их вариация, характеризующая
степень дисперсии (dispersion) данных.
• Две разные выборки могут отличаться как средними значениями, так
и вариациями.
• Однако, как показано, две выборки могут иметь одинаковые вариации,
но разные средние значения, либо одинаковые средние значения и
совершенно разные вариации.
Два симметричных распределения
Два симметричных распределения
колоколообразной формы с одинаковым
разбросом и разными средними
значениями
колоколообразной формы с
одинаковыми средними значениями и
разным разбросом
МЕРЫ РАССЕИВАНИЯ
• Для описания эмпирических распределений недостаточно
введения единственного числа, характеризующего ряд
измерений через их среднее значение, так как два
эмпирических распределения с одинаковыми средними
могут иметь совершенно разный вид.
• Существует пять оценок вариации данных: размах,
межквартилъный размах, дисперсия, стандартное
отклонение и коэффициент вариации.
Размах R
• Размахом (range) называется разность между наибольшим
и наименьшим элементами выборки
R  xмакс  xмин
Размах
• Размах позволяет измерить общий разброс (total spread) данных.
• Хотя размах выборки является весьма простой оценкой общего
разброса данных, его слабость заключается в том, что он никак не
учитывает, как именно распределены данные между минимальным и
максимальным элементами.
Сравнение трех выборок,
имеющих одинаковый размах
Межквартильный размах
• Межквартильный, или средний, размах — это разность
между третьим и первым квартилями выборки.
Межквартильный размах = Q3-Q1
• Эта величина позволяет оценить разброс 50% элементов и
не учитывать влияние экстремальных элементов.
• Суммарные количественные характеристики, такие как
медиана, первый и третий квартили, а также
межквартильный размах, на которые не влияют выбросы,
называются устойчивыми показателями.
Дисперсия и стандартное отклонение
• Хотя размах и межквартильный размах позволяют оценить общий и
средний разброс выборки соответственно, ни одна из этих оценок не
учитывает, как именно распределены данные.
• Дисперсия и стандартное отклонение лишены этого недостатка.
Эти показатели позволяют оценить степень колебания данных вокруг
среднего значения.
• Выборочная дисперсия — это сумма квадратов разностей между
элементами выборки и выборочным средним, деленная на величину,
равную объему выборки минус один.
Стандартное выборочное отклонение
• Наиболее практичной и широко распространенной оценкой разброса
данных является стандартное выборочное отклонение (sample standard
deviation).
• Этот показатель обозначается символом S и равен квадратному корню
из выборочной дисперсии.
• Стандартное выборочное отклонение — квадратный корень из суммы
квадратов разностей между элементами выборки и выборочным
средним, деленной на величину, равную объему выборки минус один.
S2 И S
• Ни выборочная дисперсия, ни стандартное выборочное отклонение не
могут быть отрицательными.
• Показатели S2 и S могут быть нулевыми, — если все элементы
выборки равны между собой. В этом случае размах и
межквартильный размах также равны нулю.
Дисперсия и стандартное отклонение
• Дисперсия и стандартное отклонение позволяют оценить разброс
данных вокруг среднего значения, определить, сколько элементов
выборки меньше среднего, а сколько — больше.
• Величина дисперсии представляет собой квадрат единицы измерения.
• Оценкой дисперсии является стандартное отклонение, которое
выражается в обычных единицах измерений.
• Стандартное отклонение позволяет оценить величину колебаний
элементов выборки вокруг среднего значения.
• Практически во всех ситуациях основное количество наблюдаемых
величин лежит в интервале плюс-минус одно стандартное отклонение
от среднего значения.
• Зная среднее арифметическое элементов выборки и стандартное
выборочное отклонение, можно определить интервал, которому
принадлежит основная масса данных.
Коэффициент вариации
•
Форма распределения
• Важное свойство выборки — форма ее распределения.
• Распределение может быть симметричным или асимметричным.
• Чтобы описать форму распределения, необходимо вычислить его
среднее значение и медиану.
• Если эти два показателя совпадают, переменная считается
симметрично распределено.
• Если среднее значение переменной больше медианы, ее
распределение имеет положительную асимметрию.
• Если медиана больше среднего значения, распределение переменной
имеет отрицательную асимметрию.
• Положительная асимметрия возникает, когда среднее значение увеличивается до
необычайно высоких значений. Отрицательная асимметрия возникает, когда среднее
значение уменьшается до необычайно малых значений. Переменная является симметрично распределенной, если она не принимает никаких экстремальных значений ни в
одном из направлений, так что большие и малые значения переменной уравновешивают друг друга
Форма распределения
• Данные, изображенные на панели А, имеют
отрицательную асимметрию. На этом рисунке виден
длинный хвост и перекос влево, вызванные наличием
необычно малых значений. Эти крайне малые
величины смещают среднее значение влево, и оно
становится меньше медианы.
• Данные, изображенные на панели Б, распределены
симметрично. Левая и правая половины
распределения являются своими зеркальными
отражениями. Большие и малые величины
уравновешивают друг друга, а среднее значение и
медиана равны между собой.
• Данные, изображенные на панели В, имеют
положительную асимметрию. На этом рисунке виден
длинный хвост и перекос вправо, вызванные
наличием необычайно высоких значений. Эти
слишком большие величины смещают среднее
значение вправо, и оно становится больше медианы.
Анализ данных на основе пяти базовых
показателей
• Min Q1 медиана, Q3, Max.
Данные распределены симметрично
• Расстояние от Xmin до медианы равно расстоянию от медианы до
Хmax
• Расстояние от Хmin до Q1 равно расстоянию от Q3 до Хmax
• Расстояние от Q1 до медианы равно расстоянию от медианы до Q3
Данные распределены несимметрично:
• Если распределение имеет положительную асимметрию:
• расстояние от Xmin до медианы меньше расстояния от медианы до
Xmax;
• расстояние от Q3 до Xmax больше расстояния от Xmin до Q1.
• Если распределение имеет отрицательную асимметрию:
• расстояние от Хmin до медианы больше расстояния от медианы до
Xmax;
• расстояние от Q3 до Xmax меньше расстояния от Xmin до Q1.
ВЫЧИСЛЕНИЕ ОПИСАТЕЛЬНЫХ СТАТИСТИК
ДЛЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
• Математическое ожидание равно сумме всех значений генеральной
совокупности, деленной на объем генеральной совокупности N.
• Дисперсия генеральной совокупности равна сумме квадратов
разностей между элементами генеральной совокупности и
математическим ожиданием, деленной на объем генеральной
совокупности.
• Стандартное отклонение генеральной совокупности (population
standard deviation) равно квадратному корню, извлеченному из
дисперсии генеральной совокупности.
Эмпирическое правило
• Эмпирическое правило гласит: если данные имеют колоколообразное
распределение, то приблизительно
• 68% наблюдений отстоят от математического ожидания не более чем
на одно стандартное отклонение,
• приблизительно 95% наблюдений отстоят от математического
ожидания не более чем на два стандартных отклонения
• и 99% наблюдений отстоят от математического ожидания не более
чем на три стандартных отклонения.
Правило Бьенамэ-Чебышева
• Более ста лет назад математики Бьенамэ и Чебышев независимо друг
от друга открыли полезное свойство стандартного отклонения. Они
обнаружили, что для любого набора данных, независимо от формы
распределения, процент наблюдений, лежащих на расстоянии не
превышающем k стандартных отклонений от математического
ожидания, не меньше
• Правило Бьенамэ-Чебышева. По крайней мере 3/4, или 75%, всех
наблюдений из любого набора данных содержится в интервале µ±2σ,
по крайней мере 8/9, или 88,89%, наблюдений содержится в интервале
µ±3σ, и как минимум 15/16, или 93,75% , наблюдений содержится в
интервале µ±4σ.
Сколько данных лежит вокруг
математического ожидания
• Правило Бьенамэ-Чебышева носит весьма общий характер и
справедливо для распределений любого вида. Оно указывает
минимальное количество наблюдений, расстояние от которых до
математического ожидания не превышает заданной величины.
Однако, если распределение имеет колоколообразную форму,
эмпирическое правило более точно оценивает концентрацию данных
вокруг математического ожидания.
ВЫЧИСЛЕНИЕ КОЛИЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ НА
ОСНОВЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
•
ВЫЧИСЛЕНИЕ КОЛИЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ НА
ОСНОВЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
•
ИЗОБРАЖЕНИЕ ДВУМЕРНЫХ ЧИСЛОВЫХ ДАННЫХ
• Способ исследования двумерных числовых величин — диаграмма
разброса (scatter diagram). (В программе Excel эта диаграмма
называется точечной, а в научной литературе — корреляционной)
Х
7
5
8
3
6
10
12
4
9
15
18
Y
21
15
24
9
18
30
36
12
27
45
54
60
50
40
30
20
10
0
0
5
10
15
20
КОВАРИАЦИЯ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
• Относительная сила зависимости, или связи, между двумя
переменными, образующими двумерную выборку, измеряется
коэффициентом корреляции
• Коэффициент корреляции изменяется от -1 для идеальной обратной
зависимости до +1 для идеальной прямой зависимости
• Коэффициент корреляции обозначается греческой буквой р
• Линейность корреляции (perfect correlation) означает, что все точки,
изображенные на диаграмме разброса, лежат на прямой
Выборочный коэффициент корреляции
• Выборочный коэффициент корреляции r вычисляется в соответствии
с формулой
Выборочный коэффициент корреляции
• При анализе выборок, содержащих двумерные данные, вычисляется
выборочный коэффициент корреляции, который обозначается буквой г.
• В реальных ситуациях коэффициент корреляции редко принимает точные
значения -1, 0 и +1. На рисунке приведены шесть диаграмм разброса и
соответствующие коэффициенты корреляции г между 100 значениями
переменных X и У.
• На рисунке А показана ситуация, в которой выборочный коэффициент
корреляции г равен -0,9. Прослеживается четко выраженная тенденция:
небольшим значениям переменной X соответствуют очень большие
значения переменной У, и, наоборот, большим значениям переменной X
соответствуют малые значения переменной У. Однако данные не лежат на
одной прямой, поэтому зависимость между ними нельзя назвать
линейной.
• На рисунке Б приведены данные, выборочный коэффициент корреляции
между которыми равен -0,6. Небольшим значениям переменной X
соответствуют большие значения переменной У. Обратите внимание на то,
что зависимость между переменными X и У нельзя назвать линейной, как
на рисунке А, и корреляция между ними уже не так велика.
Три вида корреляции между двумя переменными
На рисунке А, изображена обратная линейная зависимость между переменными X и
У. Таким образом, коэффициент корреляции р равен -1, т.е., когда переменная X
возрастает, переменная У убывает.
На рисунке Б показана ситуация, в которой между переменными X и У нет
корреляции. В этом случае коэффициент корреляции р равен 0, и, когда переменная
X возрастает, переменная У не проявляет никакой определенной тенденции: она ни
убывает, ни возрастает.
На рисунке В изображена линейная прямая зависимость между переменными X и У.
Таким образом, коэффициент корреляции р равен +1, и, когда переменная X
возрастает, переменная У также возрастает.
Диаграммы
разброса и
соответствующие
коэффициенты
корреляции г между 100
значениями
переменных X и У
Выборочный коэффициент корреляции
• Коэффициент корреляции свидетельствует о линейной зависимости,
или связи, между двумя переменными.
• Чем ближе коэффициент корреляции к -1 или +1, тем сильнее
линейная зависимость между двумя переменными.
• Знак коэффициента корреляции определяет характер зависимости:
прямая (чем больше значение переменной X, тем больше значение
переменной У) и обратная (чем больше значение переменной X, тем
меньше значение переменной У).
• Сильная корреляция не является причинно-следственной
зависимостью. Она лишь свидетельствует о наличии тенденции,
характерной для данной выборки.
Этические проблемы
• Исследователя подстерегают две ошибки: неверно выбранный
предмет анализа и неправильная интерпретация результатов.
• Интерпретация данных является субъективным процессом.
Разные люди приходят к разным выводам, истолковывая одни и
те же результаты.
• Следует критично относиться к информации, не только к
результатам, но и к целям, предмету и объективности
исследований.
• Британский политик Бенджамин Дизраэли: «Существует три
вида лжи: ложь, наглая ложь и статистика».
Спасибо за внимание!