и F(x 2 )
advertisement

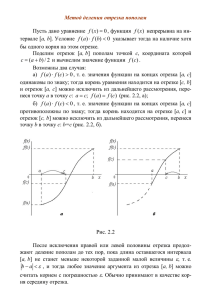
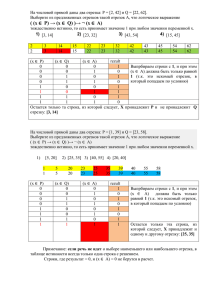
Методы нелинейного программирования МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. Они применяются для оптимизации как детерминированных, так и стохастических процессов. Общим для данных методов является то, что их используют при решении оптимальных задач с нелинейными функциями цели и ограничениями в виде нелинейных соотношений в форме равенств или неравенств. Математическая формулировка задачи нелинейного программирования: F F x ,x ,...xn 1 2 где F является количественной оценкой представляющего интерес качества объекта оптимизации. На независимые переменные можно наложить ограничения в виде равенств: (x1…xn)=0 или неравенств: (x1…xn)0. (Как правило, решения задач нелинейного программированиямогут быть найдены только численными методами.) Методы нелинейного программирования можно охарактеризовать как многошаговые методы или методы последовательного улучшения начального (исходного) решения. Большинство методов нелинейного программирования основываются на движении в n – мерном пространстве в направлении оптимума. При этом, из некоторого исходного или промежуточного состояния x(k) осуществляется переход в следующее состояние x(k+1) на величину шага x(k), т.е. xk+1=xk+xk. В случае максимального (минимального) значения должно выполняться условие: F(xk+1)>F(xx)max F(xk+1)<F(xx)min В данной группе методов при оптимизации используется информация, получаемая при сравнительной оценке величины критерия оптимальности в результате выполнения очередного шага Это численные методы поиска экстремума функции. В зависимости от числа факторов можно выделить два случая поиска оптимума: 1. Одномерный поиск, когда функция F зависит от одного фактора F=F(x) 2. Многомерный поиск, когда факторов больше одного F=F(x1,x2…xn) Одномерный поиск оптимума. МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ (МЕТОД ДИХОТОМИИ) Простейшими методами нахождения экстремума функции одной переменной является метод деления отрезка пополам (дихотомия) (интервальный метод). Рассмотрим поиск максимума на отрезке (a,b). F F( ) F(P) a P b x Разделим отрезок [a,b] пополам (т. l ). Рассчитаем значение функции в этой точке F=F (l ). Затем произвольно выбираем малое приращение x на величину (например, b a ). 10 xk+1=xk+ - это т.Р Рассчитаем F(P). Если F( )>F(P),то максимум находится в левой стороне отрезка. После этого отбрасываем правую половину отрезка (на ней нет максимума). Точку b перенесем в точку или в т.Р(обозначим за b). Если бы F( ) <F(P),то перенесли бы точку а. После переноса правого конца отрезка, задача вернулась к исходным позициям. Опять задан отрезок а b , на котором надо найти максимум. Поэтому проводим следующий цикл расчета, подобный предыдущему. Снова делим отрезок пополам, снова получаем точку на расстояние и снова переносим в середину правый или . левый конец отрезка. Величину рекомендуется 2 уменьшить Процесс может быть бесконечен. Поэтому необходимо задать какую-либо малую величину (погрешность). b-a Направление движения изменяется на противоположное с одновременным уменьшением шага в двое. xk2 xk1 ; 2 При очередном убывании целевой функции F(x) вновь меняется направление поиска, и шаг уменьшается вдвое. Метод «золотого сечения». Поиск оптимума с помощью метода «золотого сечения»основан на делении отрезка на 2 части, при этом отношение длины всего отрезка к большей его части равно отношению большей его части к меньшей. Разделим отрезок m – меньшая часть; -m – большая; на две части m и l- m m; m m m ( m)2; m 2 2 m m2 0; m2 3 m 2 0; m m а b Решаем квадратное уравнение относительно m. m 3 2 3 2 2 2 4 2 3 9 2 ; 2 2 5 2 3 5 2 2 3 5 ; m 2 3 2 5 ; m=0.382 = (1-0.618) -m=0.618 ; ; «Золотое сечение» Рассмотрим отрезок (a,b), на котором нужно найти максимум. Поиск максимума начинаем с деления отрезка слева и справа в отношении «золотого сечения», получаем точки x1 и x2: x1=a+0.382(b-a); x2=b–0.382(b-a). В этих точках вычисляются значения функции F(x1) и F(x2) и определяется новый интервал, на котором локализован экстремум F(x) Fmax а х1 х2 хопт в На отрезке [a, x1] максимума быть не может (если функция унимодальна), поэтому эту часть отрезка отбрасываем, переносим т. a в т. x1 и рассматриваем новый отрезок [a, b]. На этом отрезке уже есть точка (x2), в которой рассчитано значение F(x2). Точка x2 отсекла от прежнего отрезка справа 38,2%, Отсекает от нового (меньшего) 61,8%. Таким образом, и на новом отрезке т. x2 является точкой золотого сечения. Теперь ее можно назвать точкой x1 и добавить на уменьшенном отрезке только одну т. x2. Данная процедура Продолжается до достижения заданной степени точности: b a . Таким образом, на каждом этапе расчета, кроме первого, необходимо рассчитывать значение функции F только в одной точке, что повышает эффективность метода. Методы многомерного поиска (функция более чем одного фактора) Рассмотрим простейший вариант – оптимизацию без ограничений. Покоординатный спуск. Рассмотрим поиск максимума для случая с двумя факторами. В качестве начальной приближенной функции с двумя переменными f(x1,x2). Выбираются координаты начальной точки 0 0 поиска x1н и x 2 н ,т.е. те значения ,от которых начинается поиск оптимума. Выбираются приращения факторов (шаги) H1и H2 и малые приращения x1 и x2. Выбор этих величин определяется физическим смыслом задачи. Рассчитывается F(x1H,x2H) – точка 1. x2 F 14 13 10 x2 12 16 9 11 8 15 7 M0 x1 1 2 3 4 5 6 x1 Далее, движемся по оси x1, изменяя фактор x1 на каждом шаге на величину H1 (или –H1). При этом величина x2 остается постоянной, т.е. решаем одномерную задачу. Движемся до тех пор, пока растет F. В точке 6 значение F меньше, чем в точке 5. Поэтому возвращаемся в точку 5, фиксируем теперь x1 и изменяем x2 с шагом H2 (точка 7,8,9,10). Снова движемся по оси x1 (11,12,13), меняем направление (14,15) . Во всех точках вокруг т.12 функция F меньше, чем в данной. Следовательно, достигнута область максимума и, поэтому, необходимо уменьшить шаг и продолжать поиск меньшими шагами (т.16). Уменьшение шага может производиться несколько раз до тех пор, пока H1x1, H2x2 В этом случае поиск заканчивается, и выбираем лучшую точку за оптимум. Метод сканирования. Метод сканирования заключается в последовательном просмотре значений критерия оптимальности в ряде точек и нахождении среди них такой точки, в которой критерий оптимальности (F) имеет оптимальное (max или min) значение. Применяется данный метод к непрерывным функциям. Сканированием можно исследовать как функцию одной, так и нескольких переменных. Рассмотрим одномерное сканирование – поиск максимума функции одной переменной. Итак, имеем интервал (отрезок) a,b, на котором требуется отыскать экстремум целевой функции. Его называют интервал неопределенности функции. Точку экстремума не обязательно определять абсолютно точно. Достаточно сильно сузить интервал. Например, если мы знаем, что оптимальная температура заключена в интервале 380-3810, то большая точность и не нужна. Это обусловлено промышленными условиями регулировки температуры (10). Таким образом, в одномерном случае задача поиска экстремума сводится к сужению интервала неопределенности. Выберем целое число K значений целевой функции, которое необходимо рассчитать. BA x ; Рассчитаем интервал x. K 1 F(x) Fmax а хопт 2 x в Отложим от точки а до b интервал x. В каждой точке рассчитаем значение F(x). Принимаем за максимум наибольшее из полученных значений. К концу расчета интервал неопределенности составит 2x. Максимум может находиться либо справа, либо слева от полученной наилучшей точки. Новый интервал неопределенности - 2b a k 1 Новый интервал снова разбивается на интервалы величиной x ba x , k 1 в каждой точке рассчитываются значения F и выбирается экстремальное и т.д. Поиск продолжается до тех пор, пока b-a.