Коллоквиум. Динамика 1.

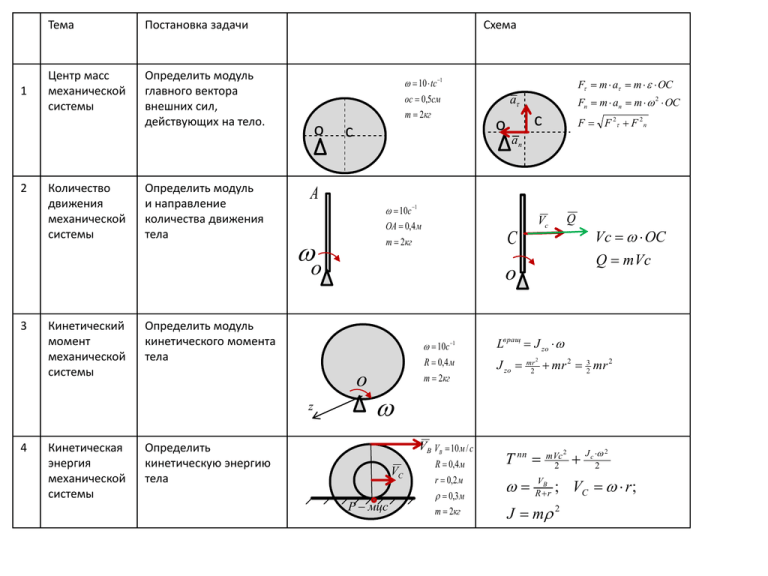
1
2
Тема
Постановка задачи
Центр масс
механической
системы
Определить модуль
главного вектора
внешних сил,
действующих на тело.
Количество
движения
механической
системы
Определить модуль
и направление
количества движения
тела
Схема
  10  tс 1
ос  0,5см
m  2кг
о
с
Кинетический
момент
механической
системы
Кинетическая
энергия
механической
системы
с
о
F  F 2  F 2 n
A
  10с 1
OA  0,4 м
m  2кг

Q
Vc
C
о
Определить модуль
кинетического момента
тела
о
z
4
Fn  m  an  m   2  OC
a
an
о
3
F  m  a  m    OC
  10с 1
R  0,4 м
m  2кг
Vc    OC
Q  mVc
Lв ращ  J zo  
J zo 
mr 2
2
 mr 2  32 mr 2

VB VB  10 м / с
Определить
кинетическую энергию
тела
VС
Р  мцс
R  0,4 м
r  0,2 м
  0,3 м
m  2кг
T пп 

mVс 2
2
VB
Rr

J с  2
2
; VC    r ;
J  m 2
Пример1
Тело массы m = 2кг движется согласно закону
S = 2t2 + 1(M). Определить модуль главного вектора внешних сил, действующих на
тело.
s
N
Решение: Теорема о движении центра масс системы.
о
G
max  Fx
e
ax  s  4
4m  F  8н
Пример 2
Диск массы m = 8кг приводит в движение тело А, движущееся со
скоростью V = 8t M/c. Определить модуль главного вектора внешних сил,
действующих на диск.
V
с
V
А
Vс
x
Vc  V2  4t
acx  Vc  4
Решение: Теорема о движении центра
масс системы.
macx  Fx
e
m4  Fx  32н
e
Пример 3
К телу 1 приложена сила F= 20н, m1 = 8кг,.
Определить ускорение тела 1 в момент времени t = 0,5c, если относительно его
движется тело 2 массой m2 = 2кг по закону S = cosπt (м).
s
F
N2
2
1
N1
из определения центра масс
x (m1  m2 ) xc  m1 x1  m2 x2
G2
G1
Теорема : (m1  m2 )acx  F
x2  x1  s
дифференцитуем дважды
(m1  m2 ) xc  m1x1  m2 x2
(m1  m2 )ac  m1a1  m2 (a1   2 cos t )
m1a1  m2 (a1   cos t )  F
2
a1 
( F  2 m2 cost )
m1  m2
20
 10
 2м / с2
Пример 4. Угловая скорость кривошипа ОА равна ωОА=2с-1.
ОА = 0,8м. Определить количество движения шатуна АВ, если его масса m = 2кг.
B
VB
O
600
Q0
Vс
Решение.
Q  m  Vс
C
90
Определим VC.
VA  OA  OA  1,6 м / с
A
VA
CP  ( AP)  ( AC )
2
AC 
AB
2

OBsin 600
2
VС   AB  CP  ? м / с
2
 0,7
VС   AB  CP  0,67  2,5  1,7 м / с
AP  OP  OA  2  OB  OA  4OA  OA  2,4
CP  (2,4) 2  (0,7) 2  2,5
 AB  VAP  12,,64  0,67
A
ωAB
Q  m Vc  2 1,7  3,4кг  м / с
Р- МЦС
Vx
Пример 5 Самолет летит горизонтально со скоростью
V=600км/ч. Из самолета прыгает парашютист и через 15 с
опускается на землю, испытывая силу сопротивления R=mV.
Определить скорость приземления парашютиста.
Решение: Начальные условия
V
t
для парашютиста :
dV

при t0  0; Vx  600км / ч
R
mdV
dt
dV
dt
 mg  R
 g  V  разделим
dV
g V
 dt
  dt
t0
 (ln( g  V )  ln g )  t
ln
g V
g
e t 
 (mg  mV )
mg переменные
y
V0
V y  V0  0
dQy
dt
g V
 t
g V
g
 V  ge t  g
V  g (1  e t )
V  g (1  e 15 )  9,8(1  e115 )  9,8 м / с
Пример 6. Барабан, момент инерции которого J, вращается вокруг оси
z, проходящей через точку О. К барабану приложен момент
сопротивления Mc. Радиус барабана R. Масса груза равна m.
Определить
-угловое ускорение барабана .

Решение: Теорема об изменении к.м.
Mc
yo
o xo
dLoz
 M ez
dt
V  R
Loz  J  mV  R
Z
G2
G1
M e z  G1  R  M c
Loz  ( J  mR )
2
V
J  mR    mgR  M
2
с
mg R  M с

J  mR 2
Пример 7 Однородная прямоугольная плита массой m укреплена c помощью петли
и удерживается в горизонтальном положении тросом АВ. Определить угловую
скорость плиты через 2 секунды после обрыва нити. Ширина плиты b=1м.
x
A
mb
3
d
dt
2
J z  M z
M e z  G  b2 
B
G
d mgb
 2
dt
3g
 2b  14,7
d
e 
Jz
 Mz
dt
e 
z
b
y
Решение: Дифференциальное уравнение движения
mgb
2
Jz 
mb 2
3
d  14,7 dt
интегрируем

t
0
0
 d   14,7dt
  14,7t  29,4c 1
r
VB
B
С
P-мцс
Vc 
VB
2
 2м / с
Пример 8
Дано Масса однородного диска m=4кг .
Скорость точки B диска VB=4м/с.
Диск катится без скольжения.
Определить кинетическую энергию
VC
диска.
1
1
2
2
T = mVc + I cω
2
2
Vc
ω=
r
1 2
I C = mr
2
2
V
1
1
1
2
2
2
C
3
кгм 2
T  mVc   mr  2  4 mVc  12 с 2
2
2 2
r
Пример 9. Ролик 1вращается под действием момента М=10нм. Масса ролика
m1=4кг. Радиус R1=0,4м. Каток 2 катиться по неподвижной поверхности без
проскальзывания. R2=2r2=0,6м. Радиус инерции катка ρ= 0,4м. Масса катка m2=8кг.
Система начала двигаться из состояния покоя. Определить угловую скорость ω1
ролика после 5 его оборотов.
Теорема об изменении кинетической
энергии
VB2= VB1
в интегральной форме для неизменяемой
B2
B1 M
2
ω1 системы при T0=0
c
Vc
е 
TA
1
p
J1 
m1R12
2
VB2  VB1  1R1
2 
T
 0,32; J 2  m2   1,28.
2
VB 2
B2 P
1 
2
m2Vc 2
2

Vc  2CP  2 R2 
1R1 R2
r2  R2
J2
2
2
2
Выразим все кинематические
характеристики через ω1,
которую надо найти.
1R1
 r2  R2  r2  R2
VB2
J1
2
T  T в р1  T пп 2
(*)
2  0,441
VC  0,271
T  T1  T2  0,57
2
1
Кинетическая энергия системы:
Найдем работу внешних сил
A( e)  AM  AG1  AG2  FN  AFтр
N
AG1  AG2  FN  AFтр  0
M
2
c
Vc
Fтр
G2
1
G1
A( e)  AM  M    10  2  5  314 Нм
Подставляем все в (*)
0,57ω21=314;
ω1=24,47с-1