Расстояния в пространстве
advertisement

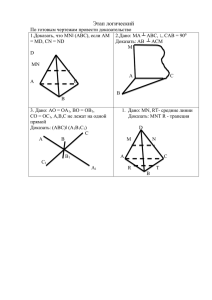
Расстояния в пространстве Расстояние между двумя точками Найдите расстояние между точками Р и Н – серединами скрещивающихся рёбер: а) куба с ребром, равным а; Задача 1. Решение. а) (рис. 1) РК АD, АK = KD ∆РКН K = 90, РK = а KH 1 a 2 DB 2 2 2 2 a a 6 2 a PH 2 P , H a B 4 2 2 2a 2 a 6 H a Ответ:4 2 2 Найдите расстояние между точками Р и Н – серединами скрещивающихся рёбер: б) тетраэдра, все рёбра которого равны а. Задача 1. AOS , O 90 AOS ,ASOa, 90AO o AS a, a AO 2 2 3 a o a 3 AOS , O 90 o AS a, AO a 3 2 a a 2 a 2 SO a 2 SO 2 a 3 3 a a 23 3 2 SO a o o 3 PKH , K 90 3 PKH , K 90 PKH , K1 90o 1 a a PK SO 1PK aSO 2 6 PK SO 2 6 2 6 a a KH AO KH aAO KH AO 3 3 3 2 2 2 a a a 2 2a 2 a PH a a aa PH PH 6 3 Ответ: 2 6 3 6 23 2 Найдите расстояние между точками Р и Н – серединами скрещивающихся рёбер: DB 3 a 2 3 a 6 Задача 1. SO со стороной основания, в) правильной четырёхугольной пирамиды 2 2 2 равной а, и правильнымKP треугольником в ,диагональном сечении. ( ABC ), K DB DK KO, DB 3 a 2 3 a 6 DB 13 a 2a 36 a 6 SOPK SO 22 24 2 KP ( ABC ), K DB , DK KO , KP2) (ABCD ABC ), , KKF DB , DK KO, FH CB , CF 1 a 6 1 a 6 PK SO 3 PK SO o 2 4 KFH , F 90 , KF a 2 4 4 2) ABCD , KF CB, CF FH 2) ABCD , KF CB, CF FH 1 3 FH, Fa, 90 o , KF 3 a KFH , F 90 o , KF a KFH 4 4 4 1 1 FH a, FHKH a, 9 a 2 1 a 2 a 10 4 4 SO – правильный, 1) ∆SDB 2 2 2 16 9 2 1 2 a 10 KH a a 16 16 4 16 4 9 2 1 2 a 10 KH a a a 6 16 , 16K 904o , PK 3) PKH , 4 a 6 a 6 3) PKH , K 90 o , PK 3) ,PKH , K 90 o , PK 2 , a 10 6a4 10a 2 4 a 10 KH , PH 4 Ответ: а KH , PH 16 a 10 4 6a 2 1016 a2 6a 2 10a 2 KH , PH a a 4 16 16 16 16 a Задача №2. На рёбрах А1В1 и В1С1 прямоугольного параллелепипеда ABCDA1B1C1D1 соответственно точками М и L отмечены середины, на ребре AB взята точка K такая, что AK : AB = 3 : 4. Считая AB = AA1 = 1, AD = 2, найдите расстояние от точки P – точки пересечения диагонали B1D с плоскостью KLM до точки: a) D; b) D1; c) B. (Рис.4) Построение сечения: 1) ML, 2) MK, 3) KN||ML, N= KN∩BC 4) NL, 5) LMKN – сечение Нахождение точки P, где P= B1D∩(KLM) B1D (DBB1) (DBB1)∩(KLM) = EF, E = B1D1∩ML, F = KN∩DB, B1D∩(KLM) = B1D∩EF = P Нахождение расстояний D1E : EB1 = 3 : 1, DF : FB = 7 : 1, DB 5 a)DP-? EPB1 подобен DPF (по 2м углам), DP : PB1 = DF : EB1 = 7 : 2, 7 DB1 ; 9 7 DP 6 9 DP DB1 5 1 6 , , , б) D1P - ? в) BP - ? Проведем через точку P прямую TW || DB, TDD1, WBB1. TP DP 7 7 7 , TP DB 5, PW PB1 2 9 9 2 5. 9 TD1 2 2 2 , TD1 1 , WB 7 9 9 7 7 WB 1 . 9 9 4 49 5 TD1 P : D1 P 81 81 PW PWB : PB 7 DP 6; Ответ: 9 249 9 20 49 69 81 81 9 D1 P 249 ; 9 PB 69 . 9 Координатный метод В(х2; у2; z2) А(х1; у1; z1) AB ( x1 x2 ) ( y1 y2 ) ( z1 z2 ) 2 2 2 Задача 3. (МФТИ) Ребро куба ABCDA1B1C1D1 равно 1, точки Е, F и К – середины рёбер АА1, ВС и СD соответственно, а точка М расположена на диагонали В1D1 так, что В1М = 2МD1. Найти расстояние между точками: а) Е и К; б) Е и М; в) М1 и К1, где М1 – середина отрезка КМ, К1 – середина ребра С1D1; г) F и Р, где Р – середина отрезка А1К. z B1 K1 M A1 C1 Е 1 1 1 (0;0; ), K (1; ;0). F ( ;1;0), M ( 2 2 2 1 1 1 2 1 0; ), K (1; ;0). F ( ;1;0), M ( ; ;1), C1 (1;1;1), D1 (1;0;1) 2 1 1 2 2 2 3 3 D1 P 2 1 1 1 1 B F C 3 2 0 1 3 2 3 1 5 ; 5 ; 1 ; M M1 K ; ; 2 2 6 12 2 2x A D 2 4 1 1 29 EM 1 1 6 EK 1 , 9 9 4 6 M 1 E y 4 FP 0 4 2 9 1 13 16 4 4 Ответ: EK A1 (0;0;1) 0 1 3 ; 1 1 51; 51 ; 1 K 1 (1; ;1) P( ; ; ) 2 2 2 2 2 2 64 12 M 1 K1 1 1 1 41 36 144 4 12 6 29 41 13 , EM , M 1 K1 , FP 2 6 12 4 Расстояние между фигурами Если среди всех расстояний между точками, одна из которых принадлежит фигуре F1, а другая - фигуре F2, существует наименьшее, то его называют расстоянием между фигурами F1 и F2. Расстояние от точки до прямой A a B C Расстояние от точки до прямой – длина отрезка перпендикуляра, опущенного из данной точки на данную прямую. AB A, a Задача №4. (рис.7) В основании прямой призмы ABCA1B1C1 лежит равнобедренный треугольник с прямым углом при вершине С, боковое ребро призмы равно меньшей стороне основания. В грани AA1C1C точкой O отмечен центроид этой грани. Считая AC = a, найдите расстояние до прямой BO от точки: A1 a) A1; b) B1; c) C1. B1 C1 1)AC = BC = AA1 = а, ACB=90, O AA1C1C, C1CBB1 – квадраты A 2) (рис.8) AC1 B, AB AC1 C1 B a 2 тогда BO – медиана и высота, C1O BO , C1O C1 , BO B a C C1 Рис.7 O a 2 2 A Рис.8 B 3)(рис.9) B1 A1 AC BC A1C BC , т.е. AC пр( АВС ) А1С C1 A1CB прямоуголь ный. O A1 N BO , A1 N A1 , BO A B a 2 S A1CB S A1OB 1 a 2 aa 2 2 2 1 a2 2 a2 2 a 2 A , CO 2 2 4 2 Рис.7 C S A1OB 1 a2 2 a2 2 a 2 , CO 2 2 4 2 1 2 2 a a 6 BO N a 4 2 1O S A1OB BO A1 N 2 a2 C 2 B Рис.9 a 2 A1 N a 6 3 2 2 2a 2 a 6 BO a 4 2 1 S A1OB BO A1 N 2 a2 2 2 4 a A1 N a 6 3 2 2 4) (рис.10) 1 S MM1B1B 2 S OB1B 2 OB B1 K , где B1 K OB , B1 K B1 , OB 2 A B S MM1B1B a 6 M B1 K , OB OB 2 O S MM1B1B BB1 MB a MB 1 1 M 2 a a 5 MB a 4 2 2 a2 5 S MM1B1B 2 a2 5 a 30 B1 K 2 6 a 6 2 M Рис.10 B B C Рис.11 Ответы : A1 , BO a 3 a 30 6 a 2 C1 , BO 2 B1 , BO Расстояние от точки до плоскости A B C . pис.12 Расстояние от точки до плоскости – длина отрезка перпендикуляра, опущенного из данной точки на данную плоскость. A, AB Пусть надо найти расстояние от точки А до плоскости β и пусть точка А лежит в плоскости α, α∩β= с. Проведём АВс, ВPc, (α,β) = PBC, ANPB. c AB c PB c ( PBA), AB PB B AN c AN ( PBA), , c AN AN PB AN , , A, AN c PB B На рёбрах АВ и АD куба ABCDA1B1C1D1 соответственно точками P и Q отмечены середины. Считая ребро куба равным а, найдите расстояние до плоскости С1PQ от точки: а) С; б) А1; в) D. Задача № 5 (рис.14 ) а) С(АВС), AC DB AC QP , QP AC E QP // DB C1 D1 B1 A1 ЕС пр( АВС) ЕС1 EC1 QP ЕС QP N EC1 QP EC QP C1 EC ((C1 PQ), ( ABC )) EC ( ABC ) (C1 PQ) D Q A CN EC1 CN C; (C1 PQ) C E P CC1 E C 90 0 CE CC1 CN CC1 a EC 1 3 3 CE AC a 2 4 4 a 3a 2 a 3a 2 2 4 3a 4 17 9a 2 2 4 a 2 17 2 a 16 B б) (рис.15) А1(А1В1С1), (А1В1С1)∩(С1PQ)=b, b // QP, C1E ∩ AA1 = A2, AA2 : A1A2=AE : A1C1=1:4, , A1A2 = b C1 D1 4a 3 A1 B1 A1C1 b A1C1 A2 (( A1 B1 C1 ), (C1 PQ)) A2 C1 b a M D A1M A2C1 A1M = ρ/A1,( С1PQ)/ Q A C1 A1 A2 C E P A 4a A1 900 a 2 4a a 2 4a 3 A1C1 a 2 A1M 2 a 17 16a 2 3 34 2a 4a 3 9 A1 A2 3 2 B в) (рис.16) D(ABC), (ABC)∩(C1PQ)=PQ, PQ ∩ DC = T, TD : DC= 1 : 2, TC1 ∩ DD1 = D2, DD2 : DD1 = 1 : 3, DD2= a/3. DR PQ D2 RD (( ABC ), (C1 PQ)) RD 2 PQ D1 B1 A1 a DF RD2 , DF = ρD,(C1PQ) D2 DR C1 D2 a a a a D 90 0 3 3 2 2 2 2 a a DF DD 2 a 17 17 3 a2 a2 a 3 2 2 9 8 DR 2 2 F T D C Q E R A Рис.16 3a Ответ: B P 17 ; 4a 17 ; a 17 Задача №6. (рис. 17). В основании пирамиды МАВСD лежит прямоугольник, её боковое ребро МВ перпендикулярно плоскости основания и АВ : АD : МВ = = 1 : 2 : 1. Считая АВ = а, найдите расстояние до плоскости МСD от точки Р, где точка Р лежит на диагонали ВD и отношение ВР : ВD равно: а) 1 : 4; б) 1 : 2; в) 3 : 4. M АВ = МВ = а, АD = 2а. Рис.17 a E C B a BC DC N MC DC MCB (( ABC ), ( MDC )) DC ( ABC ) ( MDC ) Р = |Р,(МСD)|. K P а) ВР : ВD = 1 : 4. A 2a D 3 3 3a 9 2 9 2 3a EPK , P 900 , PE a, PK 2a , EK a a 5 4 4 2 16 4 4 3 3 a a 3a 5 P, ( MCD) 4 2 10 3a 5 4 б) ВР : ВD = 1 : 2 1 1 1 2 a EPK , P 900 , PE a, PK 2a a, EK a a2 5 2 2 4 2 1 aa a 5 P, ( MCD) 2 5 a 5 2 в) ВР : ВD = 3 : 4 1 1 a 1 2 1 2 a EPK , P 900 , PE a, PK 2a , EK a a 5 4 4 2 16 4 4 1 1 a a a 5 P, ( MCD) 4 2 10 a 5 4 Ответ: 3a 5 , 10 a 5 , 5 a 5 10 Координатный метод β ах + bу + сz + d = 0, М (х , у0, z ), 0 , M0 0 0 ax0 by0 cz0 d a b c 2 2 2 Задача №7. (МИФИ). Длина ребра куба ABCDA1B1C1D1 равна 12. На рёбрах АА1, В1С1, СD взяты точки Е, F1 и G такие, что АЕ : ЕА1 = 1 : 3, В1F1 : F1С1 = 1 : 1, СG : GD = 1 : 1. Найти расстояние от точки В1 до плоскости (ЕF1G). z F1 B1 Е(12;0;3), G(6;12;0), F1(0;6;12) C1 (ЕF1G): A1 E 12a 3c d 0 6b 12c d 6 a 12 b d 0 6a 24c 2d d 24c d 6b 12c d 0 48c 2d 3c d 0 3d d y 12 24 d33)cd6b 7dd d d 7d5d 3 d c 11)) 51 51cc2)G 3 d 6a d 17 , a 17 17 51 17 102 51 1717 B C A D x ах + bу + сz + d = 0 D1 Рис.18 В1(0;0;12) b 5d 102 7d 5d 6d x y z d 0 7 x 5 y 6 z 102 0 102 102 102 B1 , ( EF1G) 0 0 6 12 102 49 25 36 30 110 3 110 11 Расстояние между двумя прямыми a, b 0 a, b MN Скрещивающиеся прямые Расстояние между двумя скрещивающимися прямыми – длина их общего перпендикуляра. Заметим, что расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, содержащими данные прямые. Задача № 7. (рис.19) Дан куб ABCDA1B1C1D1. Постройте общий перпендикуляр прямых A1D и ВС1. Найдите расстояние между прямыми, если ребро куба равно а. D1 C1 B1 A1 MN AD1, MN B C1, N M D A AD1 ∩ DA1 = M, BC1 ∩ CB1 = N, C B MN = |A1D,BC1|, MN = a. Задача № 8. (рис.20) (Новосибирский государственный университет). Найдите расстояние между диагоналями AD1 и DC1 двух смежных граней куба ABCDA1B1C1D1 с ребром а. z А(0;0;0), D(0;а;0), D1(0;а;а), С1(а;а;а). D1 A1 B1 MN AD1, MN DC1. C1 M N AD1 (0; a; a), D A a DC1 (a;0; a), D1 D(0;0;a) y C B x Рис.20 MN MD1 D1 D DN x AD1 D1 D y DC1 x(0; a; a) (0;0;a ) y (a;0; a) ( ya; xa; xa a ya) MN AD1 MN AD1 0 0 xa 2 xa 2 a 2 ya 2 0 MN DC1 NM DC1 0 ya 2 xa 2 a 2 ya 2 0 2 2 2 2 2 2 x y, 1 xa xa a ya 0, xa ya 0, x y 2 2 2 2 2 2 2 2 2 3 ya xa a ya 0 2 ya xa a 0 3xa a o a a a MN ( ; ; ), , NM 3 3 3 a2 a2 a2 a 3 9 9 9 3 Ответ: AD1 , DC1 a 3 4 Ещё один подход к вычислению расстояния между скрещивающимися прямыми. a q, c – прqb, A – прqa, ABc, AB = a,b В сферу радиуса R вписана пирамида ТАВС, основанием которой служит прямоугольный треугольник АВС, а высота пирамиды совпадает с ребром ТА. Боковое ребро ТВ образует с высотой пирамиды угол 60. А угол между ТВ и медианой основания СD, проведённой к гипотенузе АВ, равен 45. Какую наименьшую площадь может иметь сечение пирамиды плоскостью, проходящей через медиану СD и пересекающей ребро ТВ? Задача № 9 (рис.21) МГТУ им. Н.Э. Баумана. T 60 (ОDК), BK (ОDК), , СD (ODK) R D пр (ODK ) CD CD; TB D; OK OE OK пр (ODK ) OB O E D A R 45 B K C F ODB D 90 0 , B 30 0 , OD OKB OK KB ODK DK 2 2 R R 3 , DB R cos 30 0 CD 2 2 R 2 R R R 2 4 2 R R OD DK 2 2 R 2 DE R OK 4 2 T R S min 1 R 3 R 2 R2 6 2 2 4 16 O E R D B A K Ответ: S min R2 6 16 C F Расстояние от прямой до плоскости За расстояние от прямой до параллельной ей плоскости берут расстояние от любой (наиболее удобной для решения задачи) точки прямой до плоскости, Основанием пирамиды ТАВС служит равносторонний треугольник со стороной, равной 8, а её высота проходит через середину стороны основания АВ. Найдите площадь сечения пирамиды плоскостью, проходящей через боковое ребро ТА, если известно, что прямая, проходящая через середину высоты пирамиды и середину стороны основания ВС, параллельна секущей плоскости и находится от неё на расстоянии, равном 1. Задача № 10. (МГТУ им. Н.Э. Баумана). T ТХ || КN, Х=ТХ ∩ DN. АХ ∩ СВ=Р, ΔАРТ – искомое сечение. E ТFD=((АТР),(АВС)), K КЕ ТF, , KE = К,(АТР)= КN,(ТАР)=1. R A DR ТF, DR = 2. D B N F P C X S TAP 1 AP TF 2 BР : РC = 2 : 1, B S ABP D N X A F1 S ABP 60 AP 64 64 8 1 8 7 28 9 3 2 3 1 32 AP BF 1 2 3 Δ FDТ: 2 2 D BF1 2 32 3 3 8 7 16 3 FR 4 7 16 3 FD TF 7 FR 2 5 R F АРС, АС = 8, РС=8/3, С=60, по теореме косинусов C T 4 3 7 2 32 S ABC 3 3 Δ P F S ABC 64 3 16 3 4 7 24 7 5 S TAP 8 3 DF 7 48 28 2 5 7 7 1 24 8 7 32 2 7 5 3 5 Ответ: 4 3 7 Расстояние между параллельными плоскостями Расстояние между двумя параллельными плоскостями равно расстоянию от произвольной точки одной плоскости до другой плоскости В кубе ABCDA1B1C1D1 найти расстояние между плоскостями АВ1D1 и ВDС1, если АВ = а. (рис.27) Задача № 11. D1 C1 (АВ1D1 ) (ВDС1). P А1С D1В1 и А1С АD1, D1В1 ∩ АD1=D1, , А1С (АВ1D1), , А1С (ВDС1) A1 M N D C Докажем, что А1С D1В1 (остальное доказывается аналогично) A1C1 пр ( A D B ) A1C A1C D1 B1 A1 C1 D1 B1 1 1 1 A B А1С∩(АВ1D1) = М, А1С∩(ВDС1) = N, МN = (АВ1D1),(ВDС1), 1 a 3 MN A1C По теореме Фалеса А1М = МN = NС 3 3 Ответ: (АВ1D1),(ВDС1)= a 3 3 Если через прямую, параллельную плоскости, провести плоскость, параллельную данной плоскости, то можно находить расстояние между прямой и плоскостью как расстояние между параллельными плоскостями. а , построим плоскость β , а β. а, = ,β (СРА1) (МNС1), А1С (СРА1), , А1С, (МNС1) = (СРА1),(МNС1) = K,(СРА1) N B B N C M C A M P A D B1 C1 F E F1 B1 C1 A1 T O M1 D1 O1 K A2 Задача № 12. (МГТУ им. Н.Э. Баумана, 2004 год). A1 Найдите площадь сечения правильной треугольной призмы АВСА1В1С1 плоскостью, которая параллельна диагонали А1С боковой грани АА1С1С, проходит через середину стороны ВС основания АВС и точку М, лежащую на стороне АВ, если АМ = 2МВ, расстояние между А1С и секущей плоскостью равно 2, а высота призмы равна 2 B 2) Пусть АВ = 6х, тогда МВ = 2х, ВN = 3х. ΔМВN: (рис.30) МN2 = 4х2 + 9х2 – 2 2х 3х cos60 MN2 = 13x2 – 6x2 = 7x2, MN = x 7 PC = 2x 7 2x 3x M N P 6x A C 3) ΔM1 B1N1: (рис.32) . N1 B1 1 3x 2 3 0 S M 1 B1 N1 2 x 3x sin 60 2 2 1 B O x 7 S M 1 B1 N1 M 1 N1 B1O2 1 2 2 2 M1 O2 O K O1 A1 B1O2 3x 3 KO1 7 C1 T 4) ΔРКО1 (рис.33): 3x 3 KP KO1 KP KO1 7 9 x MO KF1 , , PO1 PO1 KF1 2 7 4 PF1 12 4 2 2 , PF1 F1O1 KF12 , F1O1 2 2 2 2 3 PO1 2 2 2 3 2 5) Sсеч= P 2 3 F1 2 K 9x 2 7 , x 3 7 MN KC1 x 7 2 x 7 9 x 27 x 2 27 2 7 MO 21 2 2 2 29 7 Ответ: Sсеч=21 3x 3 7 O1