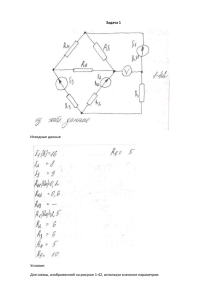
Контрольное задание Задача № 1. Расчет резистивной цепи методом преобразований.

Контрольное задание
Задача № 1. Расчет резистивной цепи методом преобразований.
Задача № 2. Расчет резистивной цепи общими методами.
Задача № 3. Расчет пассивного двухполюсника в комплексных
амплитудах.
Задача № 4. Расчет переходного процесса в цепи первого порядка
классическим методом.
Задача № 5. Расчет переходного процесса в цепи второго порядка
операционным методом.
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Методичка ниже.
Методические указания к задаче 1
В задаче 1 рассматривается резистивная цепь с одним источником
напряжения или тока и смешанным соединением резистивных элементов.
Смешанное соединение состоит из последовательного и параллельного. В
последовательном соединении все элементы находятся под одним током.
Признак последовательного соединения – два элемента или участка имеют
один общий узел. Эквивалентное сопротивление равно сумме
сопротивлений последовательно соединенных элементов.
В параллельном соединении все элементы находятся под одним
напряжением. Признак параллельности – два общих узла у всех элементов
или участков. Эквивалентная проводимость равна сумме проводимостей
параллельно соединенных элементов.
Узел – это место электрического соединения элементов или участков.
Узел может быть точкой или системой точек, соединенных
короткозамкнутыми перемычками. При анализе способа соединения
элементов узлы удобно обозначать цифрами или буквами.
В первой части задачи следует заданную цепь свернуть ко входу
(источнику), определив входное сопротивление или входную проводимость
в соответствии с изложенными методическими указаниями.
Затем, пользуясь законом Ома в виде:
u  Ri  i ,
G
i  Gu  u ,
R
последовательно определить напряжения и токи на всех участках цепи,
задав их направление в соответствии с направлением источника.
Наконец, произвести проверку полученного решения, рассчитав баланс
мощности.
Варианты приведены в Приложении 1. На схемах указаны ЭДС e в
вольтах, токи источников токов j в амперах и сопротивление элементов R в
омах. Номера элементам присваиваются произвольно, расчет производится
в общем виде, затем подставляются исходные данные.
Пример 1.1
Исходную схему на рис. 1.1, а представили в виде рис. 1.1, б
e  3 В,
R1  4 Ом,
R2  4 Ом,
R3  2 Ом,
R4  2 Ом,
R5  2 Ом,
R6  1 Ом.
3
4
2
1
5
b
a
4
2
1
d
2
b
2
6
3
4
а)
c
б)
Рис. 1.1
Преобразуем схему к узлам «ad», на которых размещен источник e .
Участок «ab» и участок «bd» имеют общий узел «b», поэтому:
Rвх  R12  R3456 .
Элементы 1 и 2 имеют общий узел «a» и «b», поэтому:
R12 
1
,
G12
G12  G1  G2 ,
G1 
1
,
R1
G2 
1
.
R2
На участке «bd» элемент 5 и участок 346 параллельны, следовательно:
R3456 
1
G3456
,
G3456  G5  G346 ,
G5 
Продолжая аналогичным образом, получим:
G346 
1
R346
,
R346  R34  R6 ,
1
.
R5
R34 
1
,
G34
G34  G3  G4 ,
G3 
1
,
R3
G4 
1
.
R4
Подставим исходные данные.
G3  G4 
1
См ,
2
R346  2 Ом ,
G3456  1 См ,
G12 
G34  1 См ,
G346 
1
См ,
2
R3456  1 Ом ,
1
См ,
2
R12  2 Ом ,
R34  1 Ом ,
G5 
1
См ,
2
G1  G2 
1
См ,
4
Rвх  3 Ом .
Теперь рассчитаем напряжения и токи.
Ток источника общий для участков «ab» и «bd» равен:
i e
Rвх
.
Напряжения на последовательных участках «12» и «3456»:
u1  iR12 ,
u5  iR3456 .
Токи на параллельных участках
«1,2»:
i1  u1G1 ,
i2  u1G2 .
«5,346»:
i5  u5G5 ,
i6  u5G346 .
Напряжение на последовательных участках «34» и «6»:
u3  i6 R34 ,
u6  i 6 R6 .
Токи на параллельных участках «3» и «4»:
i3  u3G3 ,
i4  u3G4 .
Подставим исходные данные.
i 1 A;
i1  0,5 A,
u3  0,5 B,
u1  2 B ,
u5  1 B ;
i2  0,5 A,
i5  0,5 A,
u6  0,5 B,
i3  0,25 A,
i6  0,5 A;
i4  0,25 A.
Проверим решение, составив баланс мощности.
Мощность, отданная источником,
pист  ei  3 Вт,
и мощность, полученная резисторами,
pR  u1i1  u2i2  ...  u6i6  1  1  0,125  0,125  0,5  0,25  3 ( Вт ) ,
равны, что доказывает правильность решения.
Пример 1.2
Исходную схему на рис.1.2, а, представим в виде рис.1.2, б.
a
1
b
3
2
1
2
j
3
d
d
6
4
4
2
2
5
4
c
a)
б)
Рис. 1.2
j  1 A,
R1  3 Ом,
R2  2 Ом,
R3  3 Ом,
R4  2 Ом,
R5  4 Ом,
R6  4 Ом.
Преобразуем схему к узлам источника «ad».
Эти узлы принадлежат двум участкам «123» и «456», поэтому:
Gвх  G123  G456
Участок «123» состоит из двух последовательных «1» и «23» с общим
узлом «b»:
R123  R1  R23,
а на участке «23» элементы «2» и «3» параллельны:
R23  1
Аналогично:
G23
, G23  G2  G3 , G2 
1
1
, G3 
.
R2
R3
R456  R4  R56 ,
R56  1
G56 ,
G56  G5  G6,
G5 
1
,
R5
G6 
1
.
R6
Подставим исходные данные.
G5  G6  0,25 См,
G2  G3  0,5 См,
G56  0,5 См,
R56  2 Ом ,
R23  1 Ом ,
G23  1 См,
R456  4 Ом;
R123  4 Ом;
Gвх  0,5 См.
G123  G456  0,25 См,
Рассчитаем напряжения и токи.
Напряжение на зажимах источника:
uad  j
Gвх
.
Токи параллельных участков «123» и «456»:
u
i1  ad
R123
,
u
i4  ad
R456
.
Напряжение последовательных участков «1» и «23», «4» и «56»:
u1  i1R1,
u2  i1R23;
u4  i4 R4 ,
u5  i4 R56 .
Токи параллельных участков «2» и «3», «5» и «6»:
i2  u2G1,
i3  u2G3;
i5  u5G5 ,
i6  u5G6 .
Подставим исходные данные.
uad  2 B;
u4  1 B,
i1  i4  0,5 A;
u5  1 B;
i2  i3  0,25 A,
Проверка по балансу мощности.
Мощность источника:
u1  1,5 B,
u2  0,5 B ,
i5  i6  0,25 A.
pист  uad j  2 Вт .
Мощность, потребленная резисторами:
pR  u1i1  ...  u6i6  0,75  0,125  0,125  0,5  0,25  0,25  2 ( Вт ) .
Равенство мощностей pист и р R указывает на правильность решения.
Методические указания к задаче 2
В этой задаче рассматривается линейная резистивная электрическая
цепь с несколькими источниками. Её расчет производится на основе одного
из общих методов. Одним из простейших является метод токов ветвей. Его
уравнения составляются по алгоритму
(1)  ik  0,

( 2)  ik Rk   ek .
Уравнения (1) составляются для главных сечений по ЗТК, их число
равно n y  1, где n y  число узлов.
Уравнения (2) составляются по ЗНК для главных контуров, их число
равно nв  n y  1, где nв  число ветвей с неизвестными токами.
Для выделения контуров и сечений нужно построить граф цепи,
выделить дерево графа утолщенными линиями по принципу – все узлы и ни
одного контура, остальные ветви (тонкие линии) назвать связями. Все
источники тока объединить с параллельными сопротивлениями в единые
ветви, а если это не возможно, то вырожденные ветви с источниками тока
поместить в связи, источники напряжения объединить с последовательными
сопротивлениями в единые ветви, а если такой возможности нет, то
вырожденную ветвь с источником напряжения поместить в дерево. Все ветви
построенного графа следует направить и пронумеровать, после чего
составить таблицу главных контуров и главных сечений по единому
принципу: главный контур – одна ветвь связи и остальные ветви дерева;
главное сечение – одна ветвь дерева и остальные ветви связи. Главные
контуры нумеруются и направляются ветвями связи, а главные сечения –
ветвями дерева.
Уравнения (2) для главных контуров, базирующихся на связях –
источниках тока, и уравнения (1) для главных сечений, основанных на
вырожденных ветвях дерева с источниками напряжения, не входят в систему
уравнений токов ветвей и могут быть использованы для определения
напряжений источников тока и токов источников напряжения
соответственно.
Метод токов связей продолжает предыдущий метод, используя
следующий алгоритм для k-го главного контура
ik ( R)k  ...  im ( R)km  ...  in ( R)kn  ( e)k ,
где ik , im , in  токи связей;
( R)k 
сумма
сопротивлений
ветвей
k-го
контура
(всегда
положительная);
( R)km, ( R)kn  сумма сопротивлений ветвей, принадлежащих k и
m или k и n контурам одновременно, положительная, если контуры в этих
сопротивлениях совпадают по направлению;
( e)k  сумма ЭДС в ветвях k-го контура, включая преобразованные
источники тока с параллельными сопротивлениями; все ЭДС, совпадающие с
направлением k-го контура, положительны.
Токи связей – источников токов, не объединенные с параллельными
сопротивлениями, приравниваются к токам источников и уравнения токов
связей для этих главных контуров не составляются.
Метод узловых напряжений является математическим аналогом
метода токов связей, используя алгоритм для k-го узла
uk 0 (G)k  ...  um0 (G)km  ...  un0 (G)kn  ( j )k ,
где uk 0 , um0 , un 0  узловые напряжения между k-м, m-м и n-м
узлами и 0-м (нулевым) соответственно;
( G)k  сумма
проводимостей
ветвей
k-го
узла
(всегда
положительная);
(G)km, (G)kn  сумма проводимости ветвей принадлежащих k и
m или k и n узлам одновременно (всегда отрицательная);
( j)k  сумма токов источников, токов в ветвях k-го узла, включая
преобразованные источники ЭДС с последовательными сопротивлениями,
все токи, направленные к k-му узлу, положительны.
ЭДС ветви, не объединяемой с последовательным сопротивлением,
приравнивается узловому напряжению, если 0-й узел выбрать одним из
узлов этой ветви.
В задаче 2 необходимо выполнить следующее:
- составить в общем виде уравнения токов ветвей, уравнения токов
связи и уравнения узловых напряжений;
- обосновано выбрать наименее трудоемкий метод и довести его до
численного решения;
- определить остальные напряжения и токи;
- проверить баланс мощностей.
Варианты приведены в Приложении 2. На схемах указаны ЭДС e в
вольтах, токи источников токов j в амперах и сопротивления R в омах.
Пример 2.
Исходную схему на рис. 2, а представляем в виде рис. 2, в, построив
предварительно ее граф (рис. 2, б).
Направив и пронумеровав его ветви и перенеся номера ветвей на рис.
2, в, после чего оформить исходные данные.
Выделим дерево графа и составим таблицу главных контуров и главных
сечений. Покажем на рис. 2, б для примера контур 1 и сечение 5.
Главные контуры
Главные сечения
к.1
1, 3, 6
с.3
3, 2, -1
к.2
2, 4, 5, -3
с.4
4, -2
к.7
7, 5, 6
с.5
5, -2, -7
с.6
6, -7, -1
2
1
2
(2)
20
2
10
10
1
4
3
(3)
5
20
10
(1)
6
10
7
40
7
(4)
в)
a)
(5)
2
4
3
j2  2 A ,
5
1
(1)
j1  1 A,
R2  20 Ом,
6
R3  10 Ом,
7
б)
e4  10 B,
Рис. 2
R5  20 Ом ,
R6  1 Ом,
e7  50 B,
R7  10 Ом
Уравнения для контура 1 и сечения 4, опирающиеся на вырожденные
ветви, не входят в систему уравнений токов ветвей и пока не составляются.
Остальные уравнения ЗТК для главных сечений и ЗНК для главных
контуров в соответствии с таблицами имеют вид:
i3  i2  i1  0, i1  j1,
i  i  i  0,
 5 2 7
i6  i7  i1  0,
R i  R i  R i  R i  R j  e ,
44
55
33
2 2
4
 22
 R7i7  R5i5  R6i6  e7 ,
R4  0,
где R2 j2  преобразованный в ЭДС источник тока j2 , все ЭДС,
входящие в состав контура и совпадающие с ним по направлению,
положительны.
Уравнение токов связей составим только для главных контуров,
исключая контур 1, в соответствии с приведенным ранее алгоритмом:
i2 ( R2  R5  R3 )  i1R3  i7 R5  R2 j2  e4 ,

i7 ( R7  R5  R6 )  i1R6  i2 R5  e7 ,
i  j .
1 1
После решения и определения токов i2 , i7 остальные токи (дерева)
i3 , i4 , i5 , i6 можно найти по уравнениям ЗТК для главных сечений.
Напряжения вычисляются по закону Ома, а напряжения на источник
тока j1 определяются по ЗНК для главного контура 1 как:
u1  u3  u6 .
Для того, чтобы составить уравнения узловых напряжений, выберем 0й узел на границе вырожденной ветви 4, а остальные узлы произвольно
пронумеруем (рис. 2, в) и, используя аналогичный предыдущему методу
алгоритм, запишем:
u10  e4 ,
u (G  G )  u G  u G  j  j ,
 20 2
3
10 2
30 3
1
2

u30 (G3  G5  G6 )  u20G3  u40G6  0,
u40 (G6  G7 )  u30G6   j1  G7 e7 ,
где Gk  1
Rk
,
G1  0,
k = 2, 3, 5, 6, 7; источник тока G7e7 преобразован из
источника напряжения e7 ; все источники тока, направленные к узлу, для
которого составляется уравнение, положительны.
После решения системы уравнений и определения u20 ,
u30 ,
u40
остальные напряжения определятся по ЗНК как:
u12  u10  u20  u21,
u23  u20  u30  u32 ,
u34  u30  u40  u43 .
Токи ветвей находятся по закону Ома, если взять их направление
рис. 2, б, как:
i2  u21G2 ,
i3  u23G3 ,
i6  u34G6 ,
i5  u30G5 ,
i7  (u40  e7 )G7 .
Токи вырожденных ветвей:
i4  i5  i7 ,
i1  j1 .
Для численного решения выберем уравнения токов связи, имеющие
наименьшее число уравнений:
50i2  20i7  40,

40i7  20i2  40.
i2  0,5 A,
i7  0,75 A,
i5  i2  i7  1,25 A,
i1  1 A,
i3  i1  i2  0,5 A,
i6  i7  i1  1,75 A,
i4  i2  0,5 A,
iR 2  j2  i2  1,5 A;
u4  e4  10 B,
u5  R5i5  25 B,
u3  R3i3  5 B,
u6  R6i6  17,5 B,
u2  iR 2 R2  30 B,
u1  u3  u6  22,5 B,
u7  R7i7  7,5 B.
Проверка по балансу мощностей:
 pист  j1u1  j2u2  e4i4  e7i7  115 Вт,
 pR  i2u2 i3u3  i5u5  i6u6  i7u7  115 Вт.
Баланс сошелся, значит, решение правильное.
Методические указания к задаче 3
Рассматривается линейная цепь со смешанным соединением
элементов и одним источником в установившемся гармоническом режиме.
Расчет такой цепи целесообразно производить в комплексных амплитудах
токов I m и напряжений U m . В этой форме он подобен расчету резистивной
цепи из задачи 1, только вместо сопротивлений и проводимостей следует
использовать комплексные сопротивления Z и комплексные проводимости
Y . Для элементов R, L, C они имеют вид:
Z R  R,
Z L  j L  jX L ,
Y R  G,
YL 
1
j L
j
ZC 
1
1
j
  jX C ;
jC
C
1
  jBL ,
L
YC  jC  jBC .
Складывая сопротивления последовательных участков и проводимости
параллельных, можем получить входные комплексные сопротивления или
проводимости в виде:
Z вх  Rвх  jX вх ,
Y вх  Gвх  jBвх .
На основании последних уравнений могут
эквивалентные двухэлементные двухполюсники.
быть
построены
Если теперь приравнять нулю мнимые части этих выражений и
выполнить тем самым условие резонанса, то можно получить уравнения для
определения резонансных величин 0 , R0 , G0 , L0 , C0 .
В задаче 3 нужно выполнить следующее:
- все заданные величины представить в комплексной форме;
- рассчитать комплексные амплитуды токов и напряжений всех
участков цепи, используя методику задачи 1;
- проверить полученные решения по ЗТК и ЗНК, построив векторные
диаграммы напряжений и токов;
- построить эквивалентную схему
определив параметры её элементов;
исходного
двухполюсника,
- для исходной цепи определить резонансную частоту на участке 1, 2, 3;
- построить графики частотных характеристик эквивалентных
реактивных сопротивлений или проводимостей участка 1, 2, 3.
Варианты приведены в Приложении 3.
Пример 3.1
Исходная схема представлена на рис. 3.1
Задано:
i  2 sin(1000t  135o ) A,
L0  4 мГн ,
L1  4 мГн ,
R2  20 Ом,
C3  100 мкФ .
Рис. 3.1
Расчетная схема для комплексных амплитуд построена на рис. 3.2
o
I m  2e  j135   2  j 2 A,
Z 0  j L0  j1000  4  103  j 4 Ом,
Рис. 3.2
Z 2  R2  20 Ом,
Z 1  j L1  j1000  4 103  j 4 Ом,
Z3  
j
j

  j10 Ом.
6
C
1000  100  10
Руководствуясь методическими указаниями к задаче 1, сворачиваем
схему на рис. 3.2 к зажимам источника тока I m . Участки 2 и 3 параллельны,
поэтому складываем их проводимости
Y2 
1
1

 0,05 См,
Z 2 20
Y3 
1
1

 j 0,1 См,
Z 3  j10
Y 23  Y 2  Y 3  0,05  j 0,1 См.
Участки 1 и 2, 3 последовательны. Складываем их сопротивления:
Z 1  j 4 Ом
и
Z 23 
1
Y 23

1
0,05  j 0,1

 4  j8 Ом,
0,05  j 0,1 0,052  0,12
Z1,2,3  Z 1  Z 23  j 4  4  j8  4  j 4 Ом.
Наконец, проводимости параллельных участков 0 и 1, 2, 3:
Y 1,2,3 
Y0 
1
1

  j 0,25 См,
Z 0 j4
1
1
4  j4

 0,125  j0,125,
4  j 4 42  42
Z 1,2,3

образуют входную проводимость:
Y вх  Y 0  Y 1,2,3   j 0,25  0,125  j0,125  0,125  j0,125.
В основе расчета лежат соотношения аналогичные тем, что были в
задаче 1:
U m  Z I m,
I m  YU m.
Зададим на рис. 3.2 направления токов и напряжений участков,
соответствующие направлению заданного тока I m , и произведем расчет в
следующем порядке:
U m0 
Im
 2 j 2
1 j
(1  j ) 2

 8 2
 8 2

Y вх 0,125  j 0,125
1 j
12  12
 4 2 (1  2 j  1)   j8 2 B;
I m0  U m0 Y 0   j8 2  (  j 0,25)  2 2 A,
I m1  U m0U 1,2,3   j8 2 (0,125  j 0,125)  2  j 2 A;
U m1  I m1 Z 1  ( 2  j 2 ) j 4  4 2  j 4 2 B,
U m2  I m1 Z 23  ( 2  j 2 )( 4  j8)  4 2  j8 2  j 4 2  8 2 
 4 2  j12 2 B;
I m2  U m2 Y 2  (4 2  j12 2 )  0,05  0,2 2  j 0,6 2 A,
I m3  U m2 Y 3  (4 2  j12 2 )  ( j 0,1)  1,2 2  j 0,4 2 A.
Построим векторные диаграммы, поместив полученные в расчете
комплексные амплитуды на комплексную плоскость (рис. 3.3) в виде
векторов, совокупности которых отображают закон токов Кирхгофа (ЗТК):
I m1  I m2  I m3 ,
I m  I m0  I m1
и закон напряжений (ЗНК):
U m0  U m1  U m 2 .
Все три соотношения выполняются (рис. 3.3), что свидетельствует о
правильности расчета.
-1
0
+1
Масштаб
Рис. 3.3
Построим двухполюсник эквивалентный исходному (рис. 3.1), для чего
рассмотрим входную проводимость:
Y вх  0,125  j 0,125 См.
Вещественная
часть
соответствует
проводимости
резистора
Gвх  0,125 . Мнимая отрицательная часть соответствует индуктивной
1
1
1
проводимости, BLвх 
, откуда Lвх 

 8 ( мГн) .
 Lвх
 BLвх 1000  0,125
Оба элемента соединены параллельно (рис. 3.4)
Рис. 3.4
Для поиска резонансной частоты на участке 1, 2, 3 рассмотрим
сопротивление участка:
Z 1,2,3  Z 1  Z 23  Z 1 
1
 Z1 
Y 23
1
,
Y 2 Y 3
которое при произвольной частоте равно:
Z1,2,3  j L1 

G  jC3
1
 j L1  2

G2  jC3
G22   2C32
G2
G22   2  C32
 j ( L1 
C3
G22   2C32
).
При резонансе реактивное сопротивление участка (мнимая часть Z 1,2,3
) исчезает:
C
 L1  2 32 2  0,
G2   C3
откуда и находится резонансная частота:
 0
C3  L1G22
L1C32

100  10 6  4  10 3  25 10  4
4  10
3
Теперь
построим
частотные
сопротивлений участков 1 и 2, 3:
X 1   L1
и
4
 10 10
12
 1500 (1/с).
характеристики
X 2,3 
C3
.
G22   2C32
реактивных
Целесообразно рассмотреть следующие точки:
  0,
  0  1500 1/с,
X 1  0,
X 2,3  0,
X 2,3  X1  0 L1  1500  4 103  6 (Ом),
  ,
X 1  ,
X 2,3  0.
S
Функцию X 2,3 ( ) можно привести к виду X ( S ) 
, которая, как
a2  S 2
1
известно, имеет максимум при S  a , равный X max  . Учитывая, что
2a
S  C3 , a  G2 , получим:
G
    2 
C3
0,05
100  10 6
 500 (1/с),
X 2,3 
1
 10 Ом.
2G2
Построим частотные характеристики по этим точкам.
10
8
6
4
2
0
500
1000
1500
2000
Рис. 3.5
2500
, 1/с
Пример 3.2
Исходная схема представлена на рис. 3.6:
u  20 sin( 500t  90o ) ,
R1  10 Ом,
Рис. 3.6
L3  20 мГн ,
C2  200 мкФ ,
L0  200 мГн .
Расчетная схема для комплексных амплитуд, представлена на рис. 3.7:
Рис. 3.7
U m  20e j 90  j 20 B,
Z 1  R1  10 Ом,
o
Z2  
j
  j10 Ом,
C2
Z 3  j L3  Z 0  j L0  j10 Ом.
Входное сопротивление:
Z вх  Z 0  Z 1,2,3 ,
Z 1,2,3 
Y 1,2 
Y3 
Y 1,2 
Z 1,2,3 
1
Y1,2,3
1
Z 1,2


1
,
Y 3  Y1,2
1
,
Z1  Z 2
1
  j 0,1 См ,
j10
1
1
1 j
 0,1
 0,1
 0,05  j 0,05 См ,
10  j10
1 j
2
1
1

 10  j10 Ом ,
 j0,1  0,05  j 0,05 0,05  j0,05
Z вх  j10  10  j10  10  j 20 Ом .
Расчет напряжений и токов.
Зададим направление участков (рис. 3.7).
I m0 
Um
j 20
1  j2

 j2
 0,8  j0,4 A ,
2
2
Z вх 10  j 20
1 2
U m0  I m0 Z 0  (0,8  j0,4)  j10  4  j8 B ,
U m3  I m0 Z 1,2,3  (0,8  j0,4)  (10  j10)  8  j 4  j8  4  4  j12 B ,
I m3  U m3Y 3  (4  j12)  ( j0,1)  1,2  j0,4 A ,
I m1  U m3Y 1,2  ( 4  j12 )  (0,05  j 0,05)  0,2  j 0,2  j 0,6  0,6 
 0,4  j 0,8 A,
U m1  I m1 Z1  (0,4  j0,8)10  4  j8 B ,
U m2  I m1 Z 2  (0,4  j0,8)  ( j10)  8  j 4 B ,
Векторная
реализует ЗТК
диаграмма
I m 3  I m1  I m0
и ЗНК
U m1  U m2  U m3 ,
U m3  U m0  U m .
+1
-1
0
0,4 А; 4 В
Рис. 3.8
Законы Кирхгофа выполняются. Решение задачи найдено правильно.
Эквивалентный
двухполюсник
строится
по
найденному
Z вх  10  j 20 Ом и состоит из последовательно соединенных резистора
20
Rэкв  10 Ом и индуктивности Lэкв 
 40 мГн (рис. 3.9).
500
Рис. 3.9
Для определения резонансной частоты  0 на участке 1, 2, 3
рассмотрим:
Y 1,2,3  Y 3  Y 1,2  Y3 
1
1
1



Z 1  Z 2 j L3 R  1
1
jC2

j
1

1
R1
1
 C2
 C2
 j


 j

 L
1
 L3 R 2  1
3 R2  1
R12 

1
1
 2C 22
 2C22
 2C22

R1 


.



Приравняв мнимую часть Y 1,2,3 нулю, получим уравнение для
определения  0 , решение которого дает
 0
1
L

C22  3  R12 
 C2


1
3

4
12  20  10
4  10  10
 100 
 200  10 6



  (1/с).
Следовательно, при заданных параметрах резонанс на участке 1,2,3 не
осуществим. Построим частотные характеристики (рис 3.10):
B3 ( ) 
1
,
 L3
1
 C2
B1,2 ( ) 
,
1
2
R1 
 2C22
по следующим точкам:
   
0
B3   ,
B1,2  0

B3  0 ,
B1,2  0
1
 500 1/с,
R1C2
B1,2 
1
 0,05 См,
2 R1
B3  0,1 См.
0,1
0,05
0
1000
500
1/с
Рис. 3.10
Пересечений B3 и B1,2 нет, нет и резонанса.
Методические указания к задаче 4
В задаче 4 рассматривается линейная цепь с постоянным источником и
одним реактивным элементом в переходном процессе.
Переходный процесс возникает в цепи с реактивными элементами при
любом ее изменении, которое приводит к новому режиму с новыми
значениями напряжений на ёмкостях и токов в индуктивностях. Это
изменение называется коммутацией и осуществляется замыканием или
размыканием ключа. Момент коммутации принимается за начало отсчета
времени ( t  0 ) и условно может быть представлен совокупностью двух
бесконечно близких моментов времени до коммутации (t  0) и после
(t  0) . Правила коммутации устанавливают неизменность токов в
индуктивностях и напряжений на ёмкостях в момент коммутации:
iL ( 0)  iL ( 0) ,
uC ( 0)  uC ( 0) .
Левые части этих соотношений определяются из расчета
установившегося режима цепи до коммутации. Правые части не зависят от
коммутации и называются независимыми начальными условиями.
u L (0),
u R (0),
iR (0),
iC (0) ,
Остальные начальные условия
 du 
,
 
 dt t  0
 u dt t  0 и т.д. относятся к зависимым условиям и определяются
подстановкой независимых начальных условий в уравнения цепи,
составленные после коммутации как совокупность уравнений ЗТК и ЗНК и
уравнений элементов.
Решение этой системы дифференциальных уравнений для любой
выбранной неизвестной состоит из двух частей: установившейся и
свободной.
Установившееся решение определяется в результате расчета
установившего режима цепи, образовавшейся после коммутации,
изученными ранее методами. Если установившейся режим вызывается
постоянным во времени источником, то при расчете следует закоротить все
индуктивности и разомкнуть все ёмкости.
Свободное решение находится в виде суммы функций вида:
Aet ,
число слагаемых в решении равно порядку цепи, то есть количеству
реактивных элементов в цепи, образовавшейся после коммутации. Для цепи
первого порядка удобнее искать свободное решение в виде:
Ae
t
,
где постоянная времени  определяется как:

L
,
Rэ
или
  RэC .
Эквивалентное
сопротивление
Rэ
определяется
на
зажимах
реактивного элемента при закороченных источниках напряжения (ЭДС) и
разомкнутых источниках тока.
Постоянную интегрирования A определяют, приравнивая решение в
начальный момент времени (t  0) определенному заранее (см. выше)
начальному условию.
В задаче 4 нужно выполнить следующее:
составить
систему
дифференциальных
образовавшейся после коммутации;
уравнений
цепи,
- выбрать неизвестную и записать форму, в которой будет
определяться решение;
- определить установившее решение после коммутации;
- определить постоянную времени;
- определить начальное условие и постоянную интегрирования;
- записать решение для выбранной величины и определить еще одну
из величин в этой цепи;
- построить графики зависимостей обеих величин от времени.
Варианты приведены в Приложении 4.
Пример 4.1
Исходная схема представлена на рис. 4.1:
Задано:
j  2 A,
R1  100 Ом ,
R2  100 Ом ,
L  10 мГн .
Рис. 4.1
В исходной схеме замыкаем ключ и в образовавшейся цепи (рис. 4.2)
задаем направление ветвей. Цепь имеет два узла и три ветви, из которых
одна вырожденная с источником тока.
Для ее описания требуется одно
уравнение ЗТК
 j  i2  i1  0 ,
одно уравнение ЗНК
u1  u2  uL  0
и три уравнения элементов
Рис. 4.2
u1  R1i1 ,
u2  R2i2 ,
di
uL  L 2 .
dt
Подставив уравнения элементов в уравнения соединений, получим
исходную систему дифференциальных уравнений:
 j  i2  i1  0,


di2
R
i

R
i

L
 0.
1
1
2
2


dt
Будем искать решения для тока i2 в виде:
i2  i2 уст  i2св .
Учитывая, что установившийся режим – постоянный, закоротим
индуктивность и получим схему, представленную на рис. 4.3:
u
RR
1
R1
i2 уст  2  j 1 2 
 j

R2
R1  R2 R2
R1  R2
2
100
 1 ( A).
100  100
Рис. 4.3
Для определения постоянной времени  , найдем Rэ , разомкнув
источник тока j и рассмотрев схему на зажимах индуктивности а, в (рис. 4.4)
Rэ  Rав  R1  R2 .
а
в
Рис. 4.4
Тогда
L
L
10  10  3




Rэ R1  R2 100  100
 0,05  10  3 (c )  5  10 5 ( c ).
Решение с точностью до постоянной интегрирования:
t
i2  1  Ae 510
5
.
Цепь в установившемся постоянном режиме до коммутации имеет вид
(рис. 4.5)
i2  j  i2 ( 0)  i2 ( 0) ,
Рис. 4.5
и в соответствии с правилами коммутации
получаем
независимое
начальное
условие
i2 ( 0)  j  2 A.
Сравнивая его с решением:
i2 ( 0)  2  1  A ,
получаем: A  1,
откуда окончательно:
t
i2 (t )  1  e 510
5
.
Подставляя в исходную систему уравнений, можем найти:
t
i1(t )  j  i2 (t )  1  e 510
5
A,
t
t
5
di
  1  510 5
u L (t )  L 2  10  10  3 
e
 200 e 510 B

dt
 5  10 5 
и т. д.
При построении экспоненциальных зависимостей следует учесть, что:

при t  
e 
1
 0,368 ;
e
 2
при t  2
1
e   e2 
 0,135 ;
e2
 3
при t  3
1
e  
 0,05 ;
e3
и т. д.
2
1
0
-100
-200
Пример 4.2
Рис. 4.6
Исходная схема представлена на рис. 4.7:
Задано:
e  20 B ,
R1  20 Ом ,
Рис. 4.7
R2  60 Ом ,
C  2 мкФ .
Расчетная схема представлена на рис. 4.8:
ЗТК
ЗНК (1)
Рис. 4.8
Подставляем (2) в (1):
duc

 i2  0
dt

R1i1  uC  e


R2i2  uC  0


 i1  C
i1  iC  i2  0


u1  uC  e 
u  u  0 
 2 C




u1  R1i1



u2  R2i2


duC 
iC  C


dt
исходная
система
уравнений
Выбираем:
t
uC  uC уст  uC св  uC уст  Ae  .
Размыкаем ёмкость и находим uC уст (рис. 4.9)
uC уст 
Рис. 4.9
e
20
R2 
 60  15 ( B)
R1  R2
20  60
.
Закорачиваем источник e (рис. 4.10) и на зажимах ёмкости а, в
определяем
Rэ 
а
R1R2
 15 Ом .
R1  R2
в
Рис. 4.10
Постоянная времени
  RэC  15  2 106  3 105 (c) .
Решение с точностью до постоянной интегрирования:
t
uC  15  Ae 310
5
B.
Режим до коммутации (рис. 4.11) и независимое начальное условие.
uC  e  uC ( 0)  uC ( 0)  20 B
Постоянная интегрирования:
uC ( 0)  20  15  A,
A5B.
Окончательное решение:
t
Рис. 4.11
uC  15  5e 310
5
B
и другие величины, например,
t
i1 
Графики
5
e  uC
 0,25(1  e 310 ) A.
R1
uC (t ) и i1 (t )
2,5
25
2,0
20
1,5
15
1,0
10
0,5
5
0
Рис. 4.12
Методические указания к задаче 5
Здесь рассчитывается переходный процесс в линейной цепи второго
порядка с постоянным источником. В основе расчета лежит преобразования
Лапласа, в соответствии с которым исходная схема заменяется
операционной, напряжения u(t ) и токи i(t ) заменяются операционными
изображениями  ( p) и I ( p) , дифференциальные уравнения цепи
становятся алгебраическими с операционными сопротивлениями:
Z R ( p)  R, Z L ( p)  pL, ZC ( p) 
1
,
pC
или операционными проводимостями:
Y R ( p )  G, Y L ( p ) 
Последовательно с
источники:
Z L u ZC
1
, YC ( p)  pC.
pL
появляются дополнительные
EL  LiL ( 0) u
u ( 0)
,
EC  C
p
соответственно, которые могут быть преобразованы в эквивалентные
дополнительные источники тока:
i ( 0)
JL  L
p
u J C  Cu C ( 0) ,
соответственно. Постоянные ЭДС и токи источников токов изображаются
соответственно как:
E( p) 
e
p
j
u J( p )  .
p
При составлении операционных уравнений могут быть использованы
все методы, применяемые ранее при анализе резистивных цепей.
Решение операционных уравнений имеет вид правильной дроби,
числитель A ( p ) и знаменатель B ( p ) , которой – полиномы оператора p
Оригинал от такого изображения находится по теореме разложения
A( p )
B( p )

n A( p )
k

k 1 B( pk )
e pk t ,
где pk - корни знаменателя B( p)  0 ;
n - число корней,
B( pk ) 
dB
p  pk .
dp
В задаче 5 необходимо:
- составить операционную схему и операционные уравнения;
- получить решение в виде правильной дроби;
- применить теорему разложения и найти оригинал;
- построить график полученной функции времени.
Условие задачи 5 приведены в Приложении 5.
Пример 5.1
Исходная схема представлена на рис. 5.1:
Задано:
e  100 B, R1  50 Ом,
R2  50 Ом,
C  10 1 мкФ,
L  10 мГн.
Рис. 5.1
Операционная схема представлена на рис. 5.2
1
0
Рис. 5.2
E( p ) 
e 100

, Z1( p )  R1  50, Z L ( p)  pL  10  10  3 p,
p
p
YC ( p)  pC  10 1  10  6 p, Y2  G 2 
1
 0,02,
R2
EL  Li1( 0)  L
e 10 10 3 100

 2 10  2 ,
R1
50
J C  Cu C ( 0)  C  0  0 .
i1 ( 0) u uC ( 0) определяются из схемы цепи в установившемся режиме до
коммутации (рис. 5.3) при закороченной индуктивности и разомкнутой
ёмкости
i1 
e
 i1( 0)  i1( 0),
R1
uC  0  uC ( 0)  uC ( 0).
Рис. 5.3
Применим для расчета метод условных напряжений:


1
E ( p)  EL
U10 ( p )
 YC ( p )  Y2 ( p )  
,
 Z1( p )  Z L ( p )
 Z1( p )  Z L ( p )
e
 Li1( 0)
 1
 p
,
U10 ( p )
 pC  G2  
R

p
L
R

pL
 1

1
e  p Li1 ( 0)
100  2  10  2 p
A( p )
U10 ( p ) 


p1  R1  p L G2  pC  p 10  9 p 2  0,205  10  3 p  2 B( p )
.


B( p)  0,
p1  0,
p2  104 1/с,
p3  19 104 1/с.
B( p)  3 109 p 2  0,41 10 3 p  2 ,
u10 (t )  uC (t ) 
A( p1 ) p1t A( p2 ) p2t A( p3 ) p3t
e 
e

e

B( p1 )
B( p2 )
B( p3 )
4
4
 50  55,5 e 10 t  105,3 e 19,510 t .
Проверка:
uC ( 0)  50  55,5  105,3  0,2 B ,
по начальному условию uC ( 0)  0,2 B .
Решение можно считать правильным.
При построении графика uC (t ) (рис. 5.4) учтем, что затухание
1
, связанной с меньшим по
определяется постоянной времени  2 
p2
абсолютной величине корнем
100
50
0
Рис. 5.4
Пример 5.2
Для исходной схемы из примера 5.1 (рис. 5.1) зададим новые
значения:
e  200 В, R1  40 Ом, R2  60 Oм, C  1,0 мкФ , L  1,0 мГн .
Операционная схема представлена на рис. 5.5:
Рис. 5.5
E ( p) 
ZC ( p ) 
e 200

, Z1( p )  R1  40, Z L ( p )  pL  10 3 p ,
p
p1
1
1
e

, Z 2 ( p)  R2  60, EL  Li1( 0)  L  5 10 5 ,
pC 10 5 p
R1
J C  Cu C ( 0)  0 (рис. 5.3).
Применим для расчета метод токов связей, приняв связями ветви 1 и 2:
 I1( p )Z1( p )  Z L ( p )  ZC ( p )  I 2 ( p ) ZC ( p )  E ( p )  E L ,

 I 2 ( p )Z 2 ( p )  ZC ( p )  I1( p ) ZC ( p )  0.
Разрешим систему относительно I1 ( p ) :
I 2 ( p )  I1( p )
ZC ( p)
,
Z 2 ( p)  ZC ( p)
I1( p ) 
E ( p)  EL
Z C2 ( p )
Z1( p )  Z L ( p )  ZC ( p ) 
Z 2 ( p )  ZC ( p )

e
 Li1( 0)
p


1
1
R1  pL 

pC

1 
p 2C 2  R2 

pC 

e

  Li1( 0) pC( R2 pC  1) 
p
 


1 
 R1  pL 
 pC( R2 pC  1)  1
pC 




e  pLi1( 0) R2 pC  1C 
R1 pC  p2 LC  1R2 pC  1  1
LCR2i1( 0) p 2  p Li1( 0)  eR2C   e

p R2 LCp2  R1R2C  L  p  R1  R2 
3  10  7 p 2  17,0  10  3 p  200

p 6  10 8 p 2  34  10  4 p  100


A( p )
.
B( p )
Применим теорему разложения для нахождения оригинала i1 ( p ) :
B ( p )  0,
p1  0,
p2  2,83  10 4  j 2,94  10 4 ,
p3  2,83  10 4  j 2,94  10 4 ,
B( p)  18 108 p 2  68 104 p  100 ,
i1(t ) 
A( p1 ) A( p2 ) p2t A( p3 ) p3t

e

e ,
B( p1 ) B( p2 )
B( p3 )
A( p1 ) 200

 2 ( A) ,
B( p1 ) 100
A( p2 ) p2t
3  10  7  2,83  j 2,94 2  108  17  10  3  2,83  j 2,94   10 4  200
e


8
2
8
4
4
B( p2 )
18  10  2,83  j 2,94   10  68  10  2,83  j 2,94   10  100
4
4
 e  2,8310 t e j 2,9410 t 

281
2
92,4  99,6
2

4
4
 281
e  2,8310 t e j 2,9410 t 
 92,4  j 99,6
4
4
e  2,8310 t e j 2,9410 t

99,6
jarctg
92,4
e


4
4
o
 2,07 e  2,8310 t e j 2,9410 t  40,15 A,


4
4
o
A( p3 ) p3t
e
 2,07e  2,8310 t e  j 2,9410 t  47,15 A ,
B( p3 )
так как p2 u p3 - сопряженные комплексные числа.
Окончательно:




4 
4
o
4
o 
i1t  2  2,07e  2,8310 t  e j 2,9410 t  47,15  e  j 2,9410 t  47,15  




4
 2  4,14 e  2,8310 t cos 2,94  104 t  47,15o A.
Для построения графической зависимости i1 (t ) переведем угол (47,15о) в (-0,823 рад) и выбираем моменты времени, при которых косинус
получает значения 1, 0 и (-1), а также начальный момент t  0 .
4
1) t  0 cos(0,823)  0,68, e  2,8310 t  1, i1  4,82 A.
Сопоставляя с полученным ранее i1 ( 0)  5 A, фиксируем ошибку
5  4,82
 100  3,6 %, что допустимо для учебного расчета.
5
2) 2,94  104 t  0,823  0, cos0  1, t  0,28  104 c,
4
e  2,8310 t  0,453, i1  3,87 A.
3) 2,94  104 t  0,823 

2
, cos

2
 0, t  0,814  104 c, i1  2 A.
4) 2,94  104 t  0,823   ,
cos  1,
t  1,35  104 c,
4
e  2,8310 t  0,022, i1  1,91 A.
5) 2,94  104 t  0,823 
3
3
, cos  0, t  1,885 c, i1  2 A.
2
2
6) 2,94  104 t  0,823  2 , cos2  1, t  2,42 c,
4
e  2,8310 t  0,001, i1  2 A.
5
4
3
2
1
0
0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2
Рис. 5.6