Тема: ДИСПЕРСИЯ СВЕТА Ларионов В.В. Сегодня: понедельник, 9 мая 2016 г. Ларионов В.В.

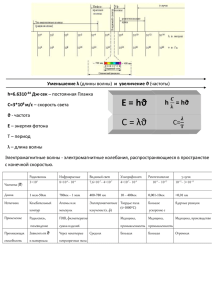
Сегодня: понедельник, 9 мая
2016 г. Ларионов В.В.
Тема: ДИСПЕРСИЯ СВЕТА
Ларионов В.В.
Дисперсией света называется зависимость показателя
преломления n вещества от частоты ν (длины волн λ) света .
Дисперсия света представляется в виде зависимости n  f (λ)
или n  f ( ν) Следствием дисперсии является разложение
в спектр пучка белого света при прохождении его через
призму .
Впервые исследовал Ньютон.
Рис
к
о
ж
з
г
с
ф
Рис. Метод скрещенных призм
*
Рис . Зависимость коэффициента преломления n от
длины волны для: 1-стекла; 2-кварца; 3-флюолита.
Величина
D= dn/dλ или dn/dν,
называемая дисперсией вещества, показывает, как быстро
меняется показатель преломления с длиной волны. Из рис 5.
λ
следует, что n для прозрачных веществ с увеличением
уменьшается; следовательно, величина dn / dλ по модулю
уменшается с ростом λ. Такая дисперсия называется
нормальной. Вблизи линий и полос поглощения, ход кривой
дисперсии n(λ)
будет иным, а именно n уменьшается с
уменьшением λ. Такой ход зависимости n от λ называется
аномальной дисперсией.
Области значения ν, в которых
dn
 0 или
dv
dn
0
dλ
соответствует нормальной дисперсии света (с ростом частоты
ν, показатель преломления n увеличивается). Нормальная
дисперсия наблюдается у веществ прозрачных для света.
*
Дисперсия называется аномальной, если dn  0 или dn  0
dν
dλ
т.е. с ростом частоты ν показатель преломления n
уменьшается. Аномальная дисперсия наблюдается в области
частот, соответствующих полосам поглощения света в данной
среде (стекло в инфракрасной и ультрафиолетовой области).
Рис .
Рис .
Молекулярная теория дисперсии
Знаем, что
n  f ( )
(1)
n 
(2)
Получается противоречие: одна и та же величина
является переменной, и в то же время, она
остается постоянной. Кроме того численное
значение для n, полученное из (2), резко расходится с
экспериментальными данными для твердых тел и
совпадает лишь для газов. Например, для воды
n=1.33, а не 9. Все эти противоречия разрешаются
очень легко, если мы вдумаемся в то, что мы
называем диэлектрической постоянной.
Во-первых, ε получена из рассмотрения
световой
волны
как
электромагнитного
колебания, скорость распространения которого
в среде зависит от диэлектрических свойств
этой среды. Обычная ε
характеризует
свойства среды в условиях постоянного
электрического поля (
). В световой волне
частота перемен поля достигает
колоссальной
E  Const
величины
.
  1015 Гц
Во-вторых,
в
электростатике
молекулу
рассматривают как упругий диполь, состоящий
из положительного и отрицательного зарядов,
между которыми действует квазиупругая сила. В
постоянном электрическом поле все молекулы
поляризуются;
их
электрический
момент
пропорционален величине наложенного поля.
Диэлектрическая постоянная зависит от величины
этих моментов. В случае переменного электрического
поля световой волны элементарные заряды, входящие
в состав молекулы, совершают быстрые колебания.
Эти колебания являются типичным примером
вынужденных колебаний. Поскольку в молекуле
отрицательные заряды (оптические электроны)
обладают значительной меньшей массой, чем
положительные заряды, постольку мы можем
считать, что в молекуле происходят колебания
отрицательного
заряда
по
отношению
к
неподвижному положительному.
Рассматривая колебания оптического
электрона, можно получить:
n0e
n  1
,
2
 0 m(0   2 )
2
или
n0 e
n  1
.
2
2
 0 m(0   )
Качественная зависимость n(ω)
показана на рисунке:
Сегодня: понедельник, 9 мая
2016 г. Лекция № 15
Поглощение света
Свет поглощается в тех случаях, когда проходящая волна
затрачивает энергию на различные процессы. Среди них:
преобразование энергии волны во внутреннюю энергию,
затраты энергии на вторичное излучение в другом диапазоне
частот, затраты энергии на ионизацию и т.д.
Интенсивность волны будет изменяться по закону Бугера
(П. Бугер (1698 – 1758) – французский ученый)
J ( x)  J 0 e
 αx
где J0 – интенсивность волны на входе в среду, α –
коэффициент поглощения, зависящий от химической
природы среды и от длины волны проходящего света,
х-толщина поглощающего слоя.
При , α  1 / x , J  J 0 / e следовательно, коэффициент
поглощения – физическая величина численно равная
обратному значению толщины слоя вещества, в котором
интенсивность волны убывает в е = 2,72 раз.
Зависимость α от λ в
общем случае имеет
сложный вид (рис.)
Рис а.
Рис б.
Физический смысл закона Бугера состоит в том,что α не
зависит от интенсивности света а, значит, и от
толщины поглощающего слоя.
Второй закон Бугера -свет может претерпевать равные
изменения, лишь встречая равное число частиц, способных
задерживать лучи или рассеивать их.
Следовательно для поглощения имеют значение не толщина, а
масса вещества, содержащаяся в этих толщинах.
α=АС,
где С-концентрация поглощающего вещества, А коэффициент, не зависящий от С.
J(x)=J0e-АСχ - закон Бера
или закон Бугера-
Ламберта - Бера.
Законы приближенные, т. к. не учитывают:
1) многократное рассеяние света;
2) зависимость показателя поглощения от λ световой волны.
*
Тепловое
излучение
Планк Макс Карл Эрнст Людвиг
(1858 – 1947) – немецкий физиктеоретик,
основоположник
квантовой
теории.
Работы
относятся
к
термодинамике,
теории теплового излучения,
теории
относительности,
квантовой теории, истории и
методологии физики, философии
науки.
Вывел
закон
распределения энергии в спектре
абсолютно черного тела. Ввел
фундаментальную постоянную с
размерностью
действия.
Формула закона Планка сразу же
получила
экспериментальное
подтверждение.
Тепловое излучение и его характеристики
Если на какое либо тело падает поток излучения
, то
Ô0 часть
этого потока отразится ,
- часть
, пропущенного
Ô1 потока
Ô2
телом,
- поглотиться Ô
телом.
3
Ô
Ô
Ô
1
2
Ô0  Ô1  Ô2  Ô3 ,
1

 3
Ô0 Ô0 Ô0
1 r b  a
(1)
(2)
r – коэффициент отражения;
b – коэффициент пропускания (прозрачности);
a – коэффициент поглощения.
В зависимости от коэффициентов r, b, a все тела можно
разделить на: 1. Идеально прозрачные, b=1. 2. Идеально
зеркальные, r=1. 3. Абсолютно черные, a=1, r, b=0.
Тепловое излучение – электромагнитное
излучение,
испускаемое
веществом
возникающее за счет его внутренней энергии.
Все другие виды свечения (излучения света),
возбуждаемые за счет любого другого вида
энергии,
кроме
теплового,
называются
люминесценцией.
Опыт показывает, что единственным видом излучения, которое
может находиться в равновесии с излучающими телами,
является тепловое излучение. Все виды люминесценции
оказываются неравновесными.
Поток энергии (любых частот), испускаемый единицей
поверхности излучающего тела в единицу времени во всех
направлениях (в пределах телесного угла 4π) называется
энергетической светимостью тела (R) или лучеиспускательной
способностью. [R] = Вт/м2.
Излучение состоит из волн различной частоты (v). Обозначим
поток энергии испускаемой единицей поверхности тела в
интервале частот от v до v + dv через dRv. Тогда при данной
температуре:
dRv ,T  rv ,T dv
(3)
где r
 спектральная плотность энергетической
v
светимости
или
спектральная
лучеиспускательная
способность тела.
rv ,T  есть функция и T соответственно и
Rv ,T  f (v, T );
Зная лучеиспускательную способность, можно вычислить
энергетическую светимость (полную или интегральную
лучеиспускательную способность тела).


RT   dRv ,T   rv ,T dv
0
или
(4)
0

RT   r ,T d
0
(5)
Закон Кирхгофа
Между испускательной и поглощательной способностью тела
существует
определенная
связь.
Мысленно
проведем
следующий эксперимент (рис.).
Рис.
Пусть внутри замкнутой оболочки находятся три тела. Тела
находятся в вакууме, следовательно обмен энергией может
происходит только за счет излучения. Опыт показывает, что
такая система через некоторое время придет в состояние
теплового равновесия (все тела и оболочка будут иметь одну и
ту же температуру).
В
таком
состоянии,
тело
обладающее
большей
лучеиспускательной способностью, теряет в единицу времени и
T  const
больше энергии, но
, следовательно
это тело должно
обладать и большей поглощающей способностью.
 rv,T


 v ,T
  rv,T
 
 
1  v ,T

r
  ...  v ,T  f v, T 

 v ,T
2
(6)
где f (v, T ) – универсальная функция Кирхгофа.
Эта функция имеет универсальный или абсолютный характер.
Густав Кирхгоф в 1856 году сформулировал закон (он же в 1862
году предложил модель абсолютно черного тела).
Отношение испускательной к поглощательной способности не
зависит от природы тела, оно является для всех тел одной и
той же (универсальной) функцией частоты и температуры.
Рис. модель абсолютно чёрного тела
Испускательная способность такого устройства (полости) очень
близка к f(v,T). Таким образом, если стенки полости
поддерживаются при температуре T, то из отверстия выходит
излучение весьма близкое по спектральному составу к
излучению абсолютно черного тела при той же температуре.
m для
T *  3200 K
Интенсивность излучения
5
Рис.
4
Спектры
излучения
абсолютно
чёрного тела при
нескольких
различных
температурах.
3
2
2400 K
1
1600 K
0
1
1,5
2
2,5
3
Видимая часть спектра
 ,10 4 см
По мере возрастания температуры максимум кривых смещается к
меньшим длинам волн. (Видимая часть спектра простирается
примерно от 4 *10 5  7 *10 5 см.)
Закон Стефана-Больцмана
Теоретическое объяснение излучения абсолютно черного
тела имело огромное значение в истории физики – оно
привело к понятию квантовой энергии.
Больцман, применив термодинамический метод к
исследованию черного излучения, показал, что это
справедливо только для абсолютно черного тела.
Площадь под кривой rν,T=f(T) равна:
R  σT
4
– закон Стефана-Больцмана.
σ  5,67  10 8 Вт  м 2  К 4
– постоянная Стефана-Больцмана.
(7)
Для универсальной функции Кирхгофа Планк вывел формулу:
2πhν
1

,
2
hν / kT
C e
1
3
rν,T
где С – постоянная величина.
Формула блестяще согласуется с экспериментальными
данными по распределению энергии в спектрах излучения
черного тела во всем интервале частот и температур.
Корпускулярно-волновой
дуализм материи
ВАВИЛОВ
Сергей Иванович
Родился 24 марта 1891 г., Москва.
Умер 25 января 1951 г., Москва.
физик, специалист в области
оптики.
Член-корреспондент по Отделению
математических и естественных
наук с 31 января 1931 г., академик
по Отделению математических и
естественных наук (физика, оптика,
люминесценция) с 29 марта 1932 г.,
президент АН СССР с 17 июля 1945
г. по 25 января 1951 г.
Фотоны. Опыт Боте
По Планку при испускании и поглощении свет ведет себя
подобно потоку частиц с энергией Е=hν, зависящей от частоты,
т.е. свет проявляет корпускулярные свойства.
Корпускула эл.м.поля (света) носит название фотона или
светового кванта.
Из закона Е=mс2 следует,что фотону можно приписать
m=Е/с2=hν/с2.
В силу того,что эл.м. волна распространяется со
скоростью света
то, очевидно, что масса покоя m0=0,так как
фотон не существует
в покоящемся состоянии, а при рождении сразу
имеет скорость с.
Очевидно, как всякая корпускула, фотон обладает
импульсом Р = mс = hν/с.
Существование фотонов убедительно
доказывается опытами Лебедева, Боте и др.
hν
Сч
Ф
При возбуждении
рентгеновскими лучами
флуоресценции энергия
распространяется не в виде
сферических волн, а в виде
направленных фотонов.
Сч
Тонкая фольга (медь, железо)
подвешивается между двумя
счетчиками (Сч).
Первичные рентгеновские
лучи (фотоны) освещали
фольгу сверху и возбуждали
свечение (флуоресценцию).
Если бы энергия излучения была
в виде сферических волн, то оба
счетчика должны реагировать
одновременно.
Опыт Ботэ.
Но счетчики реагировали независимо. Фотоны
могут попадать либо в один, либо в другой
счетчик.
Фотоэлектрический эффект
Фотоэффект – это явление, при котором
поглощение света металлами или
полупроводниками приводит к выходу
электронов за пределы облучаемого тела.
U
J1
A
K
J2
mA
V
Рис.48
-U0
0
Рис.48
J
Законы фотоэффекта
1. Закон. Фототок насыщения (т.е. число
электронов,освобождаемых светом в 1 с) прямо пропорционален лучистому потоку.
2. Закон. Максимальная кинетическая
энергия фотоэлектронов линейно возрастает с частотой падающего света и
не зависит от его интенсивности (рис 3).
Рис 3.
3. Закон. Для каждого вещества существует граничная частота или длина волны
падающего света, при которой энергия
фотоэлектронов равна нулю.Эта частота
(длина волны) называется красной
границей(Рис 4).
Рис5
Формула Эйнштейна для внешнего фотоэффекта:
mv2/2=hν-А.(*)
Уравнение(*) экспериментально
проверялось Лукирским и Прилежаевым. Результаты их исследований приведены для различных
металлов (цезий,цинк и др.) на
рис 6.
ν
Рис6.
Эйнштейн в 1905г., опираясь на гипотезу Планка о квантах,
объяснил явление фотоэффекта за что и получил Нобелевскую премию (1919 г) .
Опыты А.Ф.Иоффе и Н И.Добронравова.
В
Wi
А
L
УФ лучи
Катод (AI)
К насосу
Wi – Висмутовая пылинка r = 3*10-5 см.
L – Кварцевое окошко.
А – Анод из АI, толщиной ~ 5*10-3 мм.
В – Пластинка.
Освещение подбиралось настолько
слабым, чтобы с К срывалось около 1000
фотоэлектронов в секунду. Вырванные
электроны ускорялись полем высокого
напряжения и, ударяясь о пластинку А,
резко
тормозились,
испуская
рентгеновские лучи. Таким образом, из
антикатода А испускалось около п = 1000
рентгеновских импульсов в секунду.
Алюминиевая пластинка А толщиной порядка
5·10-3 мм и вторая, параллельная ей, пластинка В
образовывали плоский конденсатор, в котором
взвешивалась заряженная висмутовая пылинка W с
радиусом г около 3·10-5 см на расстоянии d, равном
примерно 0,02 см от антикатода А.
Пылинка время от времени теряла равновесие
— рентгеновское излучение вырывало из нее
электрон, в силу чего менялся ее заряд. Потеря
электрона происходила через различные промежутки
времени. Средний промежуток времени оказался
равным 30 минутам.
Независимые наблюдения показали, что электрон,
вырванный из пылинки, несет с собой всю энергию падающего
на него одиночного рентгеновского импульса.
С точки зрения чисто волновой теории распространения
света результаты опытов Иоффе и Добронравова совершенно
необъяснимы.
Результат опытов Иоффе и Добронравова может быть
объяснен лишь из представления о корпускулярной структуре
излучения:
1) из потока рентгеновского излучения при поглощении элек
трон воспринимает энергию одного фотона, а не
произвольное
количество энергии;
2) рентгеновский фотон, имея энергию, достаточную, чтобы
вырвать из металла тысячи электронов, поглощается только
одним
из них.
Эти опыты особенно замечательны тем, что
позволяют проследить действие отдельных фотонов.
Не следует думать, что эйнштейновское представление о
фотонах является просто возвратом к ньютоновским световым
корпускулам, крохотным комочкам материи, летящим в том или
ином направлении от источника .
Квантовая природа света проявляется в том, что
пылинка может поглотить не часть падающего на нее фотона, а
лишь весь фотон целиком.
4. Эффект Комптона.
В1924г. Артур Комптон продемонстрировал процесс, в
котором наблюдается рассеяние рентгеновского кванта
(фотона) на свободном электроне. Согласно классическим
представлениям, при рассеянии образуются фотоны с той же
энергией. В опыте наблюдались фотоны с иной энергией.
Комптон использовал фотоны
рентгеновских лучей с энергией Е=17,5Мэв.
h '
C
h
C
φ
e
θ
eРис.Схема явления Комптона.
Источник γ лучей-молибденовый антикатод, исследуемый
образец-графит.Изучался спектр лучей,рассеянных графитом
под различными углами . Для этого был применен рентгеновский спектрометр.
На рис.
представлены итоги
измерений,
сделанных
Комптоном.
Оказалось, что в спектре рассеянных лучей,
кроме линии, имеющей длину волны
излучения,
падающего
на
графит,
появляется еще одна линия с большей
длиной волны; сдвиг длины волны этой
линии по отношению к длине основной
растет с увеличением угла рассеяния 0.
Теория явления Комптона основана на
чисто корпускулярных представленияхрассеиваются две частицы: фотон и
электрон.
По закону сохранения энергии
Рис
hν+m0c2=hν+mc2
(1),
Где hν0-энергия падающего фотона, m0c2-полная энергия
свободного электрона , который мы считаем до соударения
покоящимся, hν-энергия рассеянного фотона, mс2-полная энергия
электрона после соударения.
По закону сохранения импульса (рис. ) электрон
приобретает импульс mυ, равный геометрической разности
импульсов фотона до и после соударения.
 m 
2
2
2


h
h
 h 
/
  

2

cos 

2
c
 c   c 
2
/
Решая уравнения (1) и (2) совместно, получим
h
  
vv / 1  cos   ,
m0 c
/
откуда
c
c
h
 
1  соs  ,
/
  m0 c
(2)
а так как
с

 ,
c

/
 /,
то
h
    
1  cos   .
m0 c
/
Подставляя значения констант, получим
  0,024 1  cos  A0
,
Что совпадает с результатами измерений.
Величина 0,024 называется комптоновской длиной волны.
Оптический электрон совершает вынужденные
колебания под действием следующих сил:
2
F


m

•возвращающей квазиупругой силы B
0 r , где
m и - масса и частота свободных незатухающих
колебаний электрона;
•силы сопротивления (со стороны других атомов)
Fсопр
dr
 2 m
dt
, где β – коэффициент затухания;
•вынужденные силы F  eE .
Уравнение вынужденных колебаний:
2
d r
dr
eE
2
 2
 0 r   .
2
dt
dt
m
(3)
В случае линейно-поляризованного монохроматического
света с циклической частотой ω,
, где
E0
амплитуда. Тогда
вид:
Е уравнение
Е0Cost (3) примет
eE0Cost
d 2r
dr
2
 2
 0 r  
.
2
dt
dt
m
(4)
Его решение имеет вид:
r
eE0Cos(t  0 )
m (0   )  4 
2
2 2
2
2
(5)
Если среда не поглощает свет, β=0, тогда
eE
r
.
2
2
m(0   )
(6)
Мы знаем,
вещества:
что
диэлектрическая
P
  1   1
,
0E
проницаемость
(7)
где E – мгновенное значение напряженности
электрического
поля
световой
волны,
χ
–
диэлектрическая восприимчивость среды, Р – вектор
поляризации (в данном случае его проекция на
направление внешнего поля Е), мы называли его
электрическим моментом единицы объема.
Примем что, поляризация обусловлена только
смещением валентных (оптических) электронов. Для
атомом с одним оптическим электроном P=-er (или
P  Pn0,  n0er
P=-ql), тогда
где Р – дипольный электрический момент атома,
- n0
концентрация атомов, е – заряд электрона, r –
смещение электрона. Тогда из (7), имея в виду, что
n 
получим:
n0 er
n  1
.
0E
2
(8)
Подставим (6) в (8) и получим:
n0e
n  1
,
2
2
 0 m(0   )
2
или
n0 e
n  1
.
2
2
 0 m(0   )
(9)