Пример выполнения задания 6

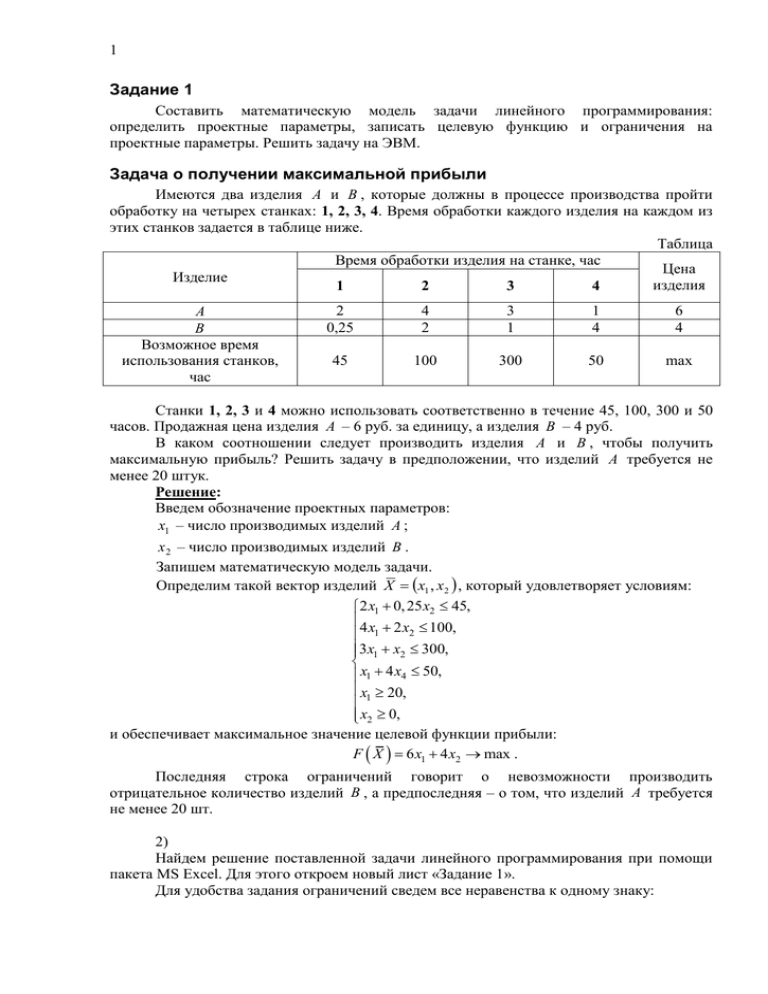
1
Задание 1
Составить математическую модель задачи линейного программирования:
определить проектные параметры, записать целевую функцию и ограничения на
проектные параметры. Решить задачу на ЭВМ.
Задача о получении максимальной прибыли
Имеются два изделия A и B , которые должны в процессе производства пройти
обработку на четырех станках: 1, 2, 3, 4. Время обработки каждого изделия на каждом из
этих станков задается в таблице ниже.
Таблица
Время обработки изделия на станке, час
Цена
Изделие
изделия
1
2
3
4
A
B
Возможное время
использования станков,
час
2
0,25
4
2
3
1
1
4
6
4
45
100
300
50
max
Станки 1, 2, 3 и 4 можно использовать соответственно в течение 45, 100, 300 и 50
часов. Продажная цена изделия A – 6 руб. за единицу, а изделия B – 4 руб.
В каком соотношении следует производить изделия A и B , чтобы получить
максимальную прибыль? Решить задачу в предположении, что изделий A требуется не
менее 20 штук.
Решение:
Введем обозначение проектных параметров:
x1 – число производимых изделий A ;
x 2 – число производимых изделий B .
Запишем математическую модель задачи.
Определим такой вектор изделий X  x1 , x2  , который удовлетворяет условиям:
2 x1  0, 25 x2  45,
4 x  2 x  100,
2
 1
3 x1  x2  300,

 x1  4 x4  50,
 x1  20,

 x2  0,
и обеспечивает максимальное значение целевой функции прибыли:
F  X   6 x1  4 x2  max .
Последняя строка ограничений говорит о невозможности производить
отрицательное количество изделий B , а предпоследняя – о том, что изделий A требуется
не менее 20 шт.
2)
Найдем решение поставленной задачи линейного программирования при помощи
пакета MS Excel. Для этого откроем новый лист «Задание 1».
Для удобства задания ограничений сведем все неравенства к одному знаку:
2
2 x1  0, 25 x2  45,
2 x1  0, 25 x2  45,
4 x  2 x  100,
4 x  2 x  100,
2
2
 1
 1
3x1  x2  300,
3x1  x2  300,


 x1  4 x4  50,
 x1  4 x4  50,
 x1  20,
 x1  20,


 x2  0,
 x2  0.
В ячейки B3: C8 листа «Задание 1» запишем коэффициенты при неизвестных
наших полученных ограничений, т.е. расходы сырья на производство единицы продукции.
В ячейки E3: E8 занесем значения правых частей неравенств ограничений, т.е. запасы
ресурсов. В ячейки B15: C15 запишем начальное значение искомых параметров x1  0 и
x2  0 . Ячейки F 3: F8 содержат значения ограничений при заданных значениях
неизвестных, т.е. формулы: =$B$15*B3+$C$15*C3. В ячейки B11: C11 запишем
параметры целевой функции: коэффициенты при неизвестных, т.е. прибыль от реализации
E12 :
единицы продукции. Саму целевую функцию поместим в ячейку
=$B$15*$B$11+$C$15*$C$11.
После заполнения таблицы необходимыми исходными данными запускаем
надстройку «Поиск решения». В появившемся окне в качестве целевой ячейки установим
ячейку E12 , укажем, что она должна быть равна максимальному значению. Изменяемыми
ячейками являются те, что содержат начальное значение неизвестных, т.е. B15: C15 .
Кроме того, необходимо «Добавить» ограничения. Т.к. ограничения имеют одинаковые
знаки, то их добавление можно проделать в одну строчку – F 3: F8  E3: E8 . Однако,
учитывая экономическую особенность задачи необходимо поставить ограничение на
целочисленное значение искомых решений (изделия нельзя производить и продавать
нецелыми) – B15: C15  целое.
После установления всех необходимых параметров поиска нажимаем кнопку
«Выполнить». Сохраняем результаты поиска решения (никаких отчетов делать
необязательно). В результате получаем, что максимальное значение целевой функции, т.е.
3
прибыли, составит Fmax  154 руб. и будет достигнуто при производстве x1  21 ед.
изделий A и x2  7 ед. изделий B . При этом все ограничения будут выполняться.
Итак, решение поставленной экономической задачи линейного программирования
найдено!
4
Задание 2
Составить математическую модель задачи линейного программирования:
определить проектные параметры, записать целевую функцию и ограничения на
проектные параметры. Решить задачу на ЭВМ.
Транспортная задача
На трех цементных заводах производится цемент одной и той же марки в
количествах соответственно 30, 40, 53 тонн. Цемент следует доставить на четыре завода
ЖБК, потребляющих его соответственно в количествах 22, 35, 25 и 41 тонн. Стоимости
(у.е.) перевозок одной тонны продукта с i -го ( i  1, 2,3 ) завода на j -й ( j  1, 2,3, 4 ) ЖБК
приведены в таблице ниже.
Спланировать перевозки так, чтобы их общая стоимость была минимальной.
Таблица
Стоимость перевозки, у.е.
Объем
Цементный
Пункты назначения производства,
завод
ЖБК-1
ЖБК-2
ЖБК-3
ЖБК-4
ai
№1
23
27
16
18
30
№2
12
17
20
51
40
№3
22
28
12
32
53
41
123/123
Объем
22
35
25
потребления, bj
Решение:
Введем матрицу обозначений проектных параметров:
 x11 x12 x13 x14 
X   x21 x22 x23 x24  ,
 x31 x32 x33 x34 
где xij – число тонн цемента, перевозимого с завода i на ЖБК- j ( i  1, 2,3 , j  1, 2,3, 4 ).
Запишем математическую модель задачи.
Определим такую матрицу тонн перевозимого цемента X , которая удовлетворяет
ограничениям:
n
i  1, m,
 xij  ai ,
j

1

 m
j  1, n,
 xij  b j ,
 i 1
 x  0,
i  1, m, j  1, n.
 ij

и обеспечивает минимальное значение целевой функции расходов:
m
n
F  X    cij xij  min .
i 1 j 1
Здесь m  3 , n  4 – число цементных заводов ( i ) и ЖБК ( j ); c ij – стоимости
перевозки 1 тонны цемента от i -го завода к j -у ЖБК; ai – объемы производства i -го
завода; b j – объем потребления j -го ЖБК.
5
Последняя строка ограничений говорит о невозможности перевозить
отрицательное количество цемента.
В нашем конкретном случае целевая функция и система ограничений примут вид:
F  X  23x11  27 x12  16 x13  18x14  12 x21  17 x22  20 x23  51x24 
22 x31  28x32  12 x33  32 x34  min ,
 x11  x12  x13  x14  30,

 x 21  x 22  x 23  x 24  40,
 x31  x32  x33  x34  53,

 x11  x 21  x31  22,

 x12  x 22  x32  35,
 x  x  x  25,
23
33
 13
 x14  x 24  x34  41,

 x11  0, x12  0, x13  0, x14  0, x 21  0, x 22  0, x 23  0, x 24  0,
 x31  0, x32  0, x33  0, x34  0.
Отметим, что количество производимого всеми заводами цемента равно общему
объему потребления цемента всеми ЖБК, т.о. транспортная задача имеет закрытый тип.
2)
Найдем решение поставленной задачи линейного программирования при помощи
пакета MS Excel. Для этого откроем новый лист «Задание 2».
В ячейки B3: E5 листа «Задание 2» запишем коэффициенты cij – расходы на
стоимость перевозки 1 тонны цемента. В ячейки F 3: F 5 занесем объем производства ai
( i  1, 2,3 ) цемента каждым заводом. В ячейки B6 : E6 занесем объем потребления b j
( j  1, 2,3, 4 ) цемента каждым ЖБК. Начальную матрицу неизвестных X со значениями
xij  0 ( i  1, 2,3 , j  1, 2,3, 4 ) зададим в ячейках B9: E11 .
Ячейки F 9 : F11 содержат ограничения на транспортировку всего производимого
на заводах цемента, т.е. содержат формулы: F 9 : =СУММ(B9:E9). Ячейки B12: E12
содержат ограничения на поставку всем ЖБК необходимого им количества цемента, т.е.
формулы: B12 : =СУММ(B9:B11).
Целевая функция записывается в ячейку G12 и имеет вид:
=СУММПРОИЗВ(B9:E11;B3:E5).
После заполнения таблицы необходимыми исходными данными запускаем
надстройку «Поиск решения». В появившемся окне в качестве целевой ячейки установим
ячейку G12 , укажем, что она должна быть равна минимальному значению. Изменяемыми
ячейками являются те, что содержат начальное значение неизвестных, т.е. B9: E11 . Кроме
того, необходимо «Добавить» ограничения. Ограничений будет три разновидности:
ограничения на полное использование производимого цемента F 9: F11  F 3: F 5 ;
ограничения на полное удовлетворение потребностей в цементе всех ЖБК
B12: E12  B6: E6 ; условие неотрицательности перевозимого количества цемента
B9: E11  0 .
6
После установления всех необходимых параметров поиска нажимаем кнопку
«Выполнить». Сохраняем результаты поиска решения (никаких отчетов делать
необязательно). В результате получаем, что минимальное значение целевой функции
расходов на перевозку цемента, составит Fmin  2221 у.е. и будет достигнуто при
следующей матрице неизвестных:
 0 0 0 30
XO   5 35 0 0  .
17 0 25 11
При этом весь производимый заводами цемент будет распределен между ЖБК и
потребность ЖБК в цементе будет полностью удовлетворена.
Итак, решение поставленной экономической задачи линейного программирования
найдено!
7
Задание 3
Мебельная фабрика выпускает стулья двух типов (стоимостью 80 и 120 руб.) На
изготовление каждого стула расходуются доски стандартного сечения, обивочная ткань и
рабочее время.
Какое количество стульев каждого типа нужно изготовить, чтобы прибыль фабрики
была максимальной? Данные о запасах и расходах сырья приведены в таблице ниже.
Таблица
Расход ингредиентов на изготовление
Кол-во
одного стула
ингредиентов в
Используемые ингредиенты
распоряжении
1 типа
2 типа
фабрики
Доски, м
2
4
440
Обивочная ткань, м
0,5
0,25
65
Рабочее время, чел./час
2
2,5
320
Стоимость, руб.
80
120
max
Решение:
Введем обозначение проектных параметров:
x1 – число изготовленных стульев 1-го типа;
x 2 – число изготовленных стульев 2-го типа.
Запишем математическую модель задачи.
Определим такой вектор продукции X  x1 , x2  , который удовлетворяет условиям:
2 x1  4 x2  440,
0,5 x  0, 25 x  65,

1
2

2 x1  2,5 x2  320,
 x1  0, x2  0,
и обеспечивает максимальное значение целевой функции прибыли:
F  X   80 x1  120 x2  max .
Последняя строка ограничений говорит о невозможности производить
отрицательное количество продукции.
2)
Найдем решение поставленной задачи линейного программирования при помощи
пакета MS Excel. Для этого откроем новый лист «Задание3».
В ячейки B3: C7 листа «Задание 3» запишем коэффициенты при неизвестных
наших полученных ограничений, т.е. расходы сырья на производство единицы продукции.
В ячейки E3: E7 занесем значения правых частей неравенств ограничений, т.е. запасы
ресурсов. В ячейки B14: C14 запишем начальное значение искомых параметров x1  0 и
x2  0 . Ячейки F 3: F 7 содержат значения ограничений при заданных значениях
неизвестных, т.е. формулы: =$B$14*B3+$C$14*C3. В ячейки B10: C10 запишем
параметры целевой функции: коэффициенты при неизвестных, т.е. прибыль от реализации
E11 :
единицы продукции. Саму целевую функцию поместим в ячейку
=$B$14*$B$10+$C$14*$C$10.
Для удобства сведем все неравенства ограничения к одному знаку:
8
2 x1  4 x2  440,
2 x1  4 x2  440,
0,5 x  0, 25 x  65,
0,5 x  0, 25 x  65,


1
2
1
2


2 x1  2,5 x2  320,
2 x1  2,5 x2  320,
 x1  0, x2  0,
 x1  0,
 x2  0.
После заполнения таблицы необходимыми исходными данными запускаем
надстройку «Поиск решения». В появившемся окне в качестве целевой ячейки установим
ячейку E11 , укажем, что она должна быть равна максимальному значению. Изменяемыми
ячейками являются те, что содержат начальное значение неизвестных, т.е. B14: C14 .
Кроме того, необходимо «Добавить» ограничения. Т.к. ограничения имеют одинаковые
знаки, то их добавление можно проделать в одну строчку – F 3: F 7  E3: E7 . Однако,
учитывая экономическую особенность задачи необходимо поставить ограничение на
целочисленное значение искомых решений (стулья нельзя производить и продавать
нецелыми) – B14: C14 цел целое.
После установления всех необходимых параметров поиска нажимаем кнопку
«Выполнить». Сохраняем результаты поиска решения (никаких отчетов делать
необязательно). В результате получаем, что максимальное значение целевой функции, т.е.
прибыли, составит Fmax  7900 руб. и будет достигнуто при производстве x1  110 ед.
стульев 1-го типа и x2  40 ед. стульев 2-го типа. При этом все ограничения будут
выполняться.
Итак, решение поставленной экономической задачи линейного программирования
найдено!