L11-1
advertisement

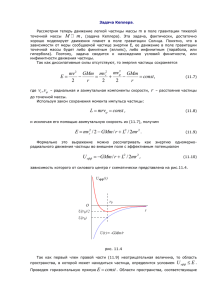
Лекция 11 Движение в поле гравитации Закон всемирного тяготения. Экспериментальное определение постоянной гравитации. Гравитационное поле, его характеристики. Задача Кеплера. Гравитационная энергия однородного шара. Гравитационный радиус. Гравитационное красное смещение. Закон всемирного тяготения. На основе наблюдательных данных Кеплер (1571-1630) установил законы движения планет Солнечной системы: - каждая планета движется по эллиптической орбите, в одном из фокусов которого находится Солнце; - радиус-вектор планеты в равные времена описывает равные площади; - квадраты периодов обращений планет относятся как кубы больших осей соответствующих эллиптических орбит. Используя эти законы, Ньютон установил закон всемирного тяготения, согласно которому любые два тела (частицы) массами m1 и m2 в вакууме притягиваются друг к другу с центральными силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними: F12 G m1m2 r12 , r122 G 6,67 108 дин см2 / г 2 – одна из фундаментальных постоянных, постоянной гравитации, r12 - расстояние между частицами (рис.11.1). где (11.1) называемая Рис. 11.1 Эти силы называются гравитационными силами, или силами всемирного тяготения. Экспериментальное определение постоянной гравитации. Опыт Кавендиша (1731-1810). Первое непосредственное доказательство закона (11.1) в лабораторных условиях и численное определение постоянной гравитации были проведены Кавендишем в 1798г. на крутильных весах (рис.11.2). Вблизи концов коромысла, укрепленными одинаковыми шариками массы m, помещались два других m , сначала в больших свинцовых шара массы M каждый, причем M положении AA , затем – BB . Из-за гравитационного притяжения шариков с шарами, коромысло поворачивался соответственно на углы 1 и 2 . Рис. 11.2 Углы измерялись смещением луча света, отраженного от зеркала З (рис.11.2). В положениях AA гравитационных закрученной нити и сил f : BB на GMm / r 2 , коромысло который f 1 GMm / r 2 ; действует крутящий уравновешивается момент упругим пары моментом f 2 GMm / r 2 , где - длина коромысла, r – расстояние между центрами шарика и ближайшего шара, f - модуль кручения, который находят из периода крутильных колебаний коромысла T 2 m 2 2f . В результате для определения G получаем формулу G 2 r2 MT 2 (1 2 ), где фигурируют только измеряемые величины. Рис. 11.3 Опыт Жолли (1809-1880). В этом методе используются рычажные весы, на левом плече которых подвешены две чашки, как это показано на рис.11.3. Между чашками неподвижно установлен тяжелый свинцовый шар с узким вертикальным каналом, сквозь который проходит нить, соединяющая чашки. Если на верхнюю чашку положить шарик массы m, то на него будет действовать вниз сила F1 mg GMm / r 2 , где r - расстояние между центрами шарика и тяжелого шара. Если шарик перевести на нижнюю чашку, то на него будет действовать сила F2 mg GMm / r 2 . Следовательно, для восстановления равновесия рычажных весов после перемещения шарика в нижнее положение, надо уменьшить груз на правом плече чашки весов на F1 F2 2GMm / r 2 , откуда и можно найти значение G . Гравитационное поле. Согласно современным представлениям тяготение между телами осуществляется, так называемыми гравитационным полем. Каждое тело создает в окружающем пространстве силовое поле, которое и действует на тела в этой области. Силовой характеристикой этого поля служит его напряженность – сила, действующая на единицу массы пробной частицы массой m , помещенной в точке r g r F / m . поля: (11.2) Это – не что иное, как ускорение свободного падения частицы в данной точке. Для поля точечной массы m оно, с помощью (11.1), (11.2) выразится формулой g (r ) Gm r. r2 (11.3) Энергетической характеристикой гравитационного поля служит его потенциал. Это гравитационный потенциал единицы массы пробной частицы: r U r / m . Для поля точечной частицы массы m имеем (11.4) r Gm / r . (13.5) Принцип независимости действия сил для полей приводит к принципу их суперпозиции: гравитационное поле, создаваемое несколькими телами, равно геометрической сумме гравитационных полей, возбуждаемых этими телами в отдельности. Математически этот принцип выражается формулами g r gi r , r i r . (11.6) На основе этих формул можно вычислить гравитационное поле любого тела. Для этого надо мысленно разбить тело на малые части, и подсчитать характеристики поля по формулам (11.3), (11.5) и (11.6). Пользуясь принципом суперпозиции, можно показать (см. задачи), что внешние гравитационные поля однородного шара и шаровой оболочки, выражаются формулами (11.3) и (11.5), и поэтому два однородных шара (сферические оболочки) притягиваются между собой так, как если бы их массы были сконцентрированы в их центрах.