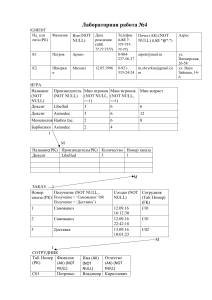
Лекция 4 (графы)

Графы
G=<V,E>
Граф ориентированный;
Граф неориентированный;
Вершины смежные;
Ребра смежные;
Петля;
Путь;
Граф связный;
Цикл;
Дерево;
Граф взвешенный.
Способы задания графов
• Матрица инцидентности
А
В
C
D
E
А
В
C
D
E
A
B
1 -1
-1 0
1
0
0
-1
0
0
0
0
C
D
E
0
0
0
0
0
-1
1
0
0
0
-1
1
1
0
-1
0
1
0
A 1 1 1 0 0 0 0 0
B 1 0 0 1 0 0 1 0
C 0 0 1 1 1 1 0 0
D 0 1 0 0 1 0 1 1
E 0 0 0 0 0 1 0 1
• Матрица смежности
А
В
C
D
E
А
В
C
D
E
A
B
C
D
E
A
B
C
D
E
A
0
B
0
C
0
D
1
E
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
1
1
0
1
0
0
A
0
B
1
C
1
D
1
E
0
1
1
1
0
1
1
1
0
1
1
1
0
0
1
1
0
0
1
1
0
• Список ребер
А
В
C
D
A A A B B C C D
B C D C D D E E
E
• Список смежности
А
В
C
D
E
A
B
C NULL
D
E
D NULL
A
C NULL
E NULL
A
C NULL
Алгоритмы обхода графа
Поиск в глубину
A
B
C
D
L
F
E
A
E
C
F
D
E
A
B
F
C
D
B
S
void step(int s,int f,int p);
Поиск в ширину
A
B
C
D
F
E
void search(int f, int las);
Q
L
A
B
E
C
D
D
F
A
B
E
C
D
F
Достижимость и алгоритм Уоршолла
A B C D E
A 0 0 1 1 0
A
B
C
D
A
B
C
D
E
A
1
1
1
1
0
E 0 0 0 0 0
E
B
1
1
1
1
0
C
1
1
1
1
0
D
1
1
1
1
0
B 1 0 0 0 1
C 0 0 0 1 1
D 0 1 0 0 0
E
1
1
1
1
1
for (i=0;i<n;i++)
for (j=0;j<n;j++)
for (k=0;k<n;k++)
if (WSM[i][j]==0)
WSM[i][j]=WSM[i][k] * WSM[k][j];
Оптимизационные алгоритмы
Кратчайшие пути из вершины s к остальным
вершинам
0
10
0
1
2
3
4
0
0
10

30

1

0
60


2
100 
0
200 150
3

20

0
40
4




0
30
20
1
3
100
60
200
2
40
4
150
V = {0, 1, 2, 3, 4}
S = {2}
Инициализируем
массив D
for (i=1;i<N;i++)
d[i]=c[2][i];
Инициализируем
массив Р
for (i=1;i<N;i++)
p[i]=2;
0
1
2
3
4
100

0
0
1
2
3
4
2
2
2
2
2
200 150
0
100
1

2
0
3
4
200 150
0
2
1
2
2
2
3
2
V = {0, 1, 2, 3, 4}
S = {2}
J=0
V/S = {0, 1, 3, 4}
w=0 D[w]=100
s={2, 0}
v=1 D[1]= 
D[0]+C[0][1]=100+10=110
D[1]=110
P[1]=0
v=3 D[3]=200
D[0]+C[0][3]=100+30=130
D[3]=130
P[3]=0
v=4 D[4]=150
D[0]+C[0][4]=100+ 
замены нет
4
2
0
1
100 110
2
0
3
4
130 150
0
2
1
0
2
2
3
0
0
10
4
2
30
20
1
3
100
60
200
2
40
4
150
Кратчайшие пути между всеми парами вершин
k
Ak-1[i][k]
i
Ak-1[k][j]
j
for (k=0;k<N;k++)
Ak-1[i][j]
for (i=0;i<N;i++)
for (j=0;j<N;j++)
if (a[i][k]+a[k][j]<a[i][j]) {a[i][j]=a[i][k]+a[k][j];
p[i][j]=k;}
Кратчайшие пути между всеми парами вершин
0
10
30
20
1
3
100
60
200
2
40
4
0
0
0
1
10
2
70
3
30
4
70
1
2
3
4
160
100
180

0
110
20

60
0
80

190
130
0

210
150
40
0
150
0
1
2
3
4
0
-1
1
-1
2
1
3
-1
4
3
2
-1
2
-1
0
-1
-1
-1
1
2
0
-1
2
-1
-1
-1
-1
-1
-1
-1
Нахождение центра ориентированного
графа
0
1
2
3
4
0
0
27
10
22
7
1
2
1
40
0
39
27
0
5
13
8
19
3
27
4
21
max 40
26
20
39
8
2
27
0
15
22
6
0
19
0
1
10
7
20
1
4
2
2
6
5
13
3
Остовные деревья минимальной стоимости
Алгоритм Прима
0
1
10
7
20
1
4
2
2
6
5
13
3
V={0, 1, 2, 3, 4}.
U={0}
0
1
1
4
2
V={0, 1, 2, 3, 4}.
U={0, 1}
3
0
1
1
V={0, 1, 2, 3, 4}.
U={0, 1, 3}
4
5
3
2
0
1
1
4
2
V={0, 1, 2, 3, 4}.
U={0, 1, 3, 4}
6
5
3
0
1
1
V={0, 1, 2, 3, 4}.
U={0, 1, 3, 4, 2}
4
2
2
6
5
3
=14
Алгоритм Крускала
0
0
1
1
1
2
1
4
2
1
4
2
2
3
3
3
4
0
1
1
4
2
2
0
1
1
4
2
2
6
5
5
3
3
Задача коммивояжера
5
0
0
11
1
3
1
2
11
6
3
2
3
2
4
2
4
5
2
4
7
8
3
5
16
4
2
4
8
5
Эйлеровы пути и циклы
2
Алгоритм построения
Эйлерова цикла:
• Строим любой цикл
1234561
•
Удаляем эти ребра из
графа
4
1
P
2
6
5
3
4
1
6
G1
• Берем вершину v  Р, v
 G1 и строим цикл
1234561
25362
3
5
2
3
4
1
6
5
Паросочетания графов
1
5
2
6
3
7
4
8
Метод чередующейся цепи
6
1
5
2
6
3
7
4
8
1
5
M: (1,5),(2,7)
MP: (6,1),(5,2),(7,4)
2
7
4
Пример:
1
5
2
6
3
7
4
8
M: 
P: (1,5)
M: (1,5)
P: (2,5),(1,5),(1,6)
M: (2,5),(1,6)
P: (2,7),(2,5),(1,5),(1,6),(6,4)
M: (2,7),(1,5),(6,4)
P: (3,7),(2,7),(2,5),(1,5),(1,6),
(6,4),(4,8)
M: (3,7),(2,5),(1,6),(4,8)