Георг Фридрих Бернард Риман

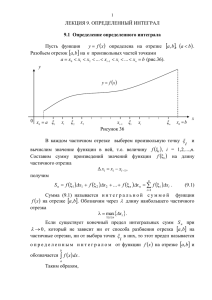
Георг Фридрих Бернхард Риман
Интеграл Римана
Выполнила студентка группы 2У00
Нагорнова Е.А.
Георг Фридрих Бернхард Риман
•
• Георг Фридрих Бернхард
Риман (нем. GeorgFriedrich-Bernhard
Riemann, 17 сентября
1826, немецкий
математик. За свою
короткую жизнь (всего
10 лет трудов) он
преобразовал сразу
несколько разделов
математики.
Биография
• Родился в семье бедного пастора, вторым из
шести его детей, в деревне Брезеленц,
недалеко от Данненберга. Мать Римана
умерла от туберкулёза, когда он ещё учился в
школе; от этой же болезни умерли две его
сестры.
• Наклонности к математике проявлялись у
молодого Римана ещё в детстве, но, уступая
желанию отца, Риман поступил в 1846 году в
Гёттингенский университет для изучения
филологии и богословия. Однако здесь он
слушает лекции Гаусса и принимает
окончательное решение стать математиком.
• 1847: переходит в
Берлинский университет,
слушает лекции Дирихле,
Якоби и Штейнера.
• 1849: возвращается в
Гёттинген. Знакомится с
Вебером, который
становится его учителем и
близким другом. Годом
позже приобретает ещё
одного друга —
Дедекинда.
• 1851: защищает
докторскую «Основания
теории функций
комплексной
переменной». В ней
Риман ввёл понятие,
позже известное как
риманова поверхность.
Научная деятельность
• В знаменитом докладе «О
гипотезах, лежащих в основании
геометрии» (нем. Über die
Hypothesen, welche der Geometrie
zu Grunde Liegеп) Риман
определил общее понятие nмерного многообразия и его
метрику в виде произвольной
положительно определённой
квадратичной формы.
• Вслед за Коши, Риман
рассмотрел
формализацию
понятия интеграла и
ввёл своё
определение —
интеграл Римана.
Развил общую теорию
тригонометрических
рядов, не сводящихся
к рядам Фурье.
Интеграл Римана
• Интегра́л Ри́ мана —
одно из важнейших
понятий
математического
анализа. Введён
Бернхардом Риманом
в 1854 году, и является
одной из первых
формализаций
понятия интеграла.
Неформальное геометрическое
описание
• Риман формализовал понятие интеграла,
разработанное Ньютоном и Лейбницем,
как площади подграфика (фигуры,
заключенной между графиком функции и
осью абсцисс). Для этого он рассмотрел
фигуры, состоящие из нескольких
вертикальных прямоугольников и
получающиеся при разбиении отрезка
(см. рисунок). Если при «размельчении»
разбиения существует предел, к которому
сходятся площади таких фигур
(интегральные суммы), этот предел
называется интегралом Римана функции
на отрезке.
Определения
• Через интегральные суммы
• Пусть на отрезке [a,b] определена
вещественнозначная функция f.
• Рассмотрим разбиение отрезка —
конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок [a,b] на n отрезков .
Длина наибольшего из отрезков δR
=max(Δxi), называется шагом разбиения,
где Δxi = xi − xi − 1-длина элементарного
отрезка.
• Отметим на каждом отрезке разбиения по
точке
• Интегральной суммой называется выражение
• Если при стремлении шага разбиения к нулю
интегральные суммы стремятся к одному и
тому же числу, независимо от выбора
• то это число называется интегралом функции f
на отрезке [a,b], т.е.
• В этом случае, сама функция f называется
интегрируемой (по Риману) на [a,b]; в
противном случае f является неинтегрируемой
(по Риману) на отрезке [a,b].
Свойства
• Невырожденность:
• Положительность: Если интегрируемая функция
f неотрицательна, то её интеграл по отрезку
[a,b] также неотрицателен.
• Линейность: Если функции f и g интегрируемы,
и
, то функция αf + βg тоже
интегрируема, и
• Непрерывность: Если интегрируемые функции
fi равномерно сходятся на отрезке [a,b] к
функции f, то f интегрируема, и
• (Последняя формула может быть получена уже
как формальное следствие свойств 1-3 и
интегрируемости предельной функции.)
• Аддитивность при разбиениях отрезка Пусть a < b < c. Функция f
интегрируема на отрезке [a,c], тогда и только тогда, когда она
интегрируема на каждом из отрезков [a,b] и [b,c], при этом
• Непрерывная на отрезке функция интегрируема по Риману (следствие
свойств 1-5). Разрывные функции могут быть интегрируемы, но могут
и не быть; примером функции, не интегрируемой по Риману, является
всюду разрывная функция Дирихле. Критерий Лебега
интегрируемости функции по Риману: функция интегрируема по
Риману на отрезке [a,b], если и только если на этом отрезке она
ограничена, и множество точек, где она разрывна, имеет нулевую
меру (то есть может быть покрыто счётным семейством интервалов со
сколь угодно малой суммарной длиной).
• Если функция F является первообразной непрерывной функции f, то
интеграл функции f на отрезке [a,b] может быть вычислен по формуле
Ньютона-Лейбница: он равен F(b) − F(a). (Это - общее свойство любых
интегралов, удовлетворяющих свойствам 1-5, а не только интеграла
Римана.) Непрерывная на отрезке функция f всегда имеет
первообразную, и каждая первообразная имеет вид:
• , где C - произвольная константа.
История
• Такое определение интеграла
дано Коши, но применялось
только для непрерывных
функций.
• Риман в 1854 году дал это же
определение без предположения
непрерывности.
•Спасибо за
внимание!!