Три признака равенства треугольников 2

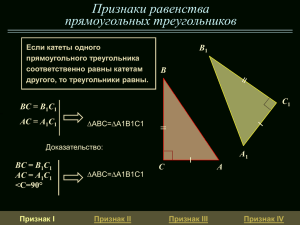
Три признака
равенства
треугольников
2
1
3
Завершить
Первый признак
Теорема
Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу
между ними другого треугольника,
то такие треугольники равны
Доказательство
Рассмотрим ∆ABC и ∆A1B1C1,
AB=A1B1, AC= A1C1, ∠A = ∠A1.
у
которых
Докажем, что ∆ABC = ∆А1B1C1 .
Так как ∠A = ∠A1, то ∆ABC можно наложить на
∆A1B1C1 так,
что вершина A совместится с вершиной A1, а
стороны AB и AC наложатся соответ-ственно
на лучи A1B1 и A1C1.
Поскольку AB=A1B1 , AC= A1C1 ,то сторона AB
совместится со стороной A1B1 ,а сторона AC –
со стороной A1C1.
Совместятся стороны BC и B1C1.
∆ABC и ∆A1B1C1 полностью совместятся,
значит, они равны. ТЕОРЕМА ДОКАЗАНА.
Доказанная
теорема
выражает
признак (равенство у треугольников
двух сторон и угла между ними), по
которому можно сделать вывод о
равенстве
треугольников.
Он
называется
ПЕРВЫМ
ПРИЗНАКОМ
РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
Второй признак
Теорема
Если сторона и два прилежащих к ней угла одного
треугольника соответственно равны стороне и
соответственно
равны
стороне
и
двум
прилежащим к ней углам другого треугольника,
то такие треугольники равны.
Доказательство
Рассмотрим ∆ABC и ∆A1B1C1, у которых
AB=A1B1, ∠A = ∠A1, ∠B = ∠B1.
Докажем, что ∆ABС = ∆A1B1C1.
Наложим ∆ABC на ∆A1B1C1 так, чтобы вершина A совместилась с
вершиной A1, сторона AB – с равной ей стороной A1B1, а вершины
C и C1 оказались по одну сторону от прямой A1B1.
Так как, ∠A = ∠A1, ∠B = ∠B1, то сторона AC наложится на луч
A1C1, а сторона BC – на луч B1C1.
Поэтому вершина C – общая точка сторон AC и BC – окажется
лежащей как на луче A1C1, так и на луче B1C1 и, следовательно,
совместится с общей точкой этих лучей – вершиной C1 . Значит,
совместятся стороны AC и A1C1, BC и B1C1.
Итак, ∆ABC и ∆A1B1C1 полностью совместятся, поэтому они
равны. ТЕОРЕМА ДОКАЗАНА.
Доказанная
теорема
выражает
признак (равенство у треугольников
стороны и двух углов прилежащих к
ней), по которому можно сделать
вывод о равенстве треугольников. Он
называется
ВТОРЫМ
ПРИЗНАКОМ
РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
Третий признак
Теорема
Если три стороны одного треугольника
соответственно равны трем сторонам другого
треугольника,
то такие треугольники равны.
Доказательство
Рассмотрим ∆ABC и ∆A1B1C1, у которых
AB=A1B1, AC = A1C1, CB = C1B1.
Докажем, что ∆ABС = ∆A1B1C1.
Приложим ∆ABC к ∆A1B1C1 так, чтобы
вершина A с вершиной A1, вершина B1 – с
B1, а вершины C и C1 оказались по
разные стороны от прямой А1В1.
Соединим
∠1 = ∠2; ∠3 точки
= ∠4 В и В1
∆А1С1С = ∆В1С1С по двум сторонам и углу
Значит,
∠А1СВ
Рассмотрим
равнобедренные
∆А1С1С и ∆В1С1С
между
ними
1 = ∠ А1С1В1
∆А1С1B1 = ∆A1B1С по двум сторонам
и углу между ними
Рассмотрим равнобедренный ∆С1В1С
∠CC1B1 = ∠C1CB1
Рассмотрим равнобедренный ∆С1А1С
∠1 = ∠2
Следовательно,
∠3 = ∠4
Таким образом,
∆С1А1В1 = ∆СА1В1
Доказанная
теорема
выражает
признак (равенство у треугольников
трех сторон), по которому можно
сделать
вывод
о
равенстве
треугольников. Он называется
ТРЕТЬИМ ПРИЗНАКОМ
РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
Из третьего признака следует, что
треугольник жесткая фигура