Метод итераций
advertisement

Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ
1 семестр
Лекция 13
Длина кривой.
Касательная и кривизна.
Приближенные методы
решения уравнений.
11 декабря 2014 года
Лектор: Профессор НИЯУ МИФИ, д.ф.-м.н.
Орловский Дмитрий Германович
Длина кривой
x f1 (t ),
y f 2 (t ),
z f (t )
3
t
Если функции f1(t), f2(t), f3(t)
непрерывно дифференцируемы,
то кривая L называется гладкой
кривой (кривая класса С1).
Условие регулярности
[ f1 '(t )]2 [ f 2 '(t )]2 [ f 3 '(t )]2 0
для спрямляемости кривой не обязательно.
Длина кривой
Теорема. Гладкая кривая спрямляема и ее длина удовлетворяет
неравенствам
m12 m22 m32 ( ) | L | M12 M 22 M 32 ( ),
где
m j Inf | f j ' (t ) |, (1 j 3),
[ ; ]
M j Sup | f j ' (t ) |, (1 j 3).
[ ; ]
Длина кривой
Рассмотрим гладкую кривую
L {( x; y; z ) : x f1 (t ), y f 2 (t ), z f 3 (t ), t }
( f1 (t ), f 2 (t ), f 3 (t ) C 1[ ; ]).
Пусть
M (t ) ( f1 (t ); f 2 (t ); f 3 (t ))
( A M ( ), B M ( )).
l (t ) | AM (t ) |
Теорема. Для любой гладкой кривой
l ' (t ) [ f1 ' (t )]2 [ f 2 ' (t )]2 [ f 3 ' (t )]2 .
M (t )
Длина кривой
Доказательство. Пусть t>t0, тогда по теореме об аддитивности длины
l (t ) l (t0 ) | M (t0 )M (t ) |
Согласно предыдущей теореме для отрезка [t0;t]
m12 m22 m32 (t t0 ) l (t ) l (t0 ) M12 M 22 M 32 (t t0 )
l (t ) l (t0 )
M 12 M 22 M 32
t t0
mi | f i ' (ξ i ) |, t 0 ξ i t , 1 i 3,
m12 m22 m32
M i | f i ' (ηi ) |, t 0 ηi t , 1 i 3.
lim ξ i lim ηi t0 lim | fi ' (ξ i ) | lim | fi ' (ηi ) || f i ' (t0 ) | .
t t0
t t0
t t0
t t0
l (t ) l (t0 )
lim
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t0
Длина кривой
Если t<t0, тогда
l (t0 ) l (t ) | M (t )M (t0 ) |
Согласно предыдущей теореме для отрезка [t; t0]
m12 m22 m32 (t0 t ) l (t0 ) l (t ) M12 M 22 M 32 (t0 t )
l (t0 ) l (t )
M 12 M 22 M 32
t0 t
mi | f i ' (ξ i ) |, t ξ i t 0 , 1 i 3,
m12 m22 m32
M i | f i ' (ηi ) |, t ηi t 0 , 1 i 3.
lim ξ i lim ηi t0 lim | fi ' (ξ i ) | lim | fi ' (ηi ) || f i ' (t0 ) | .
t t0
t t0
t t0
t t0
l (t ) l (t0 )
l (t0 ) l (t )
lim
lim
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t 0 0
t t0
t0 t
Длина кривой
l (t ) l (t0 )
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t0
lim
l (t ) l (t0 )
lim
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t0
Отсюда следует, что
l ' (t ) lim
t t 0
l (t ) l (t0 )
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t0
Длина кривой
Элемент длины дуги
Определение. Модуль дифференциала длины дуги называется
элементом длины дуги.
ds | l ' (t )dt | [ f1 ' (t )]2 [ f 2 ' (t )]2 [ f 3 ' (t )]2 | dt | (dx) 2 (dy) 2 (dz) 2
(теорема Пифагора в дифференциалах).
Особенно наглядное значение эта формула имеет для плоской
кривой, являющейся графиком явно заданной функции y=f(x).
График явно заданной функции всегда можно представить в
параметрической форме. Для этого достаточно взять в качестве
параметра независимую переменную.
Длина кривой
x t,
y f (t ),
z 0.
ds [ x' (t )]2 [ y ' (t )]2 [ z ' (t )]2 | dt |
1 [ f ' (t )]2 0 | dt | 1 [ f ' ( x)]2 | dx |
(dx) 2 (dy ) 2
ds (dx) 2 (dy ) 2
Касательная к кривой
x f1 (t ),
y f 2 (t ),
z f (t ).
3
Касательная к кривой
Предельное значение этого вектора при t→t0
a { f1 ' (t0 ); f 2 ' (t0 ); f 3 ' (t0 )}
(в том случае, когда оно отлично от нулевого вектора) называется
касательным вектором к кривой в точке t0.
Прямая, проходящая через точку M(t0) с этим направляющим
вектором, называется касательной к кривой в точке t0.
Касательная к кривой
Особые и регулярные точки кривой
x f1 (t ),
y f 2 (t ),
z f (t ).
3
[ f1 ' (t )] [ f 2 ' (t )] [ f 3 ' (t )] 0 регулярная точка
2
2
2
[ f1 ' (t )]2 [ f 2 ' (t )]2 [ f 3 ' (t )]2 0 особая точка
В регулярной точке кривая всегда имеет касательную.
Касательная к кривой
Пример 1.
x t 3 ,
3
y t ,
z 0.
Пример 2.
x t | t |,
2
y
t
,
z 0.
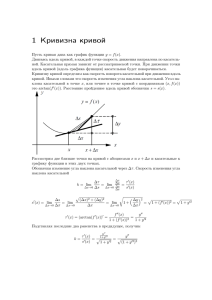
Кривизна плоской кривой
Средняя кривизна на участке:
k ср |
s
|
Кривизна в точке M(t0):
k lim kср lim
t t 0
t t 0
| |
s
Кривизна плоской кривой
Теорема. Пусть на плоскости задана гладкая регулярная кривая
x (t ),
y (t ).
Тогда ее кривизна в каждой точке t0 определяется формулой
k
| ' (t0 ) ' ' (t0 ) ' ' (t0 ) ' (t0 ) |
(| ' (t0 ) |2 | ' (t0 ) |2 )3 / 2
Замечание.
Гладкая:
, C 1
Регулярная:
| ' (t ) |2 | ' (t ) |2 0
Кривизна плоской кривой
Доказательство. Так как кривая регулярна, то величина
| ' (t ) |2 | ' (t ) |2 0
Пусть для определенности
' (t ) 0
Касательный вектор к кривой
a { ' (t ); ' (t )}
образует с осью абсцисс угол
arctg
' (t )
' (t )
Кривизна плоской кривой
По определению кривизны
(t ) (t0 )
k lim
lim
t t0 s
t t0 s ( t ) s ( t )
0
( (t ) (t0 )) / (t t0 )
lim
t t0 ( s ( t ) s ( t )) / ( t t )
0
0
lim( (t ) (t0 )) / ( t t0 )
t t0
lim( s(t ) s(t0 )) / ( t t0 )
t t0
'(t0 )
s '( t0 )
Кривизна плоской кривой
Так как
' (t ) (arctg
' (t )
1
' (t )
)'
(
)'
2
' (t )
1 ( ' (t ) / ' (t )) ' (t )
[ ' (t )]2
' ' (t ) ' (t ) ' (t ) ' ' (t ) ' (t ) ' ' (t ) ' ' (t ) ' (t )
2
2
2
[ ' (t )] [ ' (t )]
[ ' (t )]
[ ' (t )]2 [ ' (t )]2
s ' (t ) [ ' (t )]2 [ ' (t )]2 ([ ' (t )]2 [ ' (t )]2 )1/ 2
то
k
'(t ) ''(t ) ''(t ) '(t )
2
2 1/2
/
([
'(
t
)]
[
'(
t
)]
)
2
2
[ '(t )] [ '(t )]
| '(t ) ''(t ) ''(t ) '(t ) |
(| '(t ) |2 | '(t ) |2 )3/2
Кривизна плоской кривой
Пример. Найти кривизну окружности
( x a) 2 ( y b) 2 R 2
Параметрическое уравнение
R
t
x a R cos t ,
y b R sin t ,
0 t 2 .
Кривизна плоской кривой
| ' (t ) ' ' (t ) ' ' (t ) ' (t ) |
k
(| ' (t ) |2 | ' (t ) |2 )3 / 2
(t ) a R cos t , (t ) b R sin t
' (t ) R sin t , ' (t ) R cos t
' ' (t ) R cos t , ' (t ) R sin t
' (t ) ' ' (t ) ' ' (t ) ' (t ) ( R sin t )( R sin t ) ( R cos t )( R cos t ) R 2
| ' (t ) |2 | ' (t ) |2 R 2 sin 2 t R 2 cos 2 t R 2
R2
R2 1
k 2 3/ 2 3
(R )
R
R
Кривизна плоской кривой
Часто представляется удобным приближенно заменять кривую
вблизи рассматриваемой точки – окружностью, имеющую ту же
кривизну, что и кривая в данной точке.
Кругом кривизны кривой в данной точке M называется круг,
который
1) касается кривой в точке M;
2) направлен выпуклостью вблизи этой точки в ту же сторону, что
и кривая;
3) имеет ту же кривизну, что и кривая в точке M.
Центр круга кривизны называется центром кривизны, а радиус
этого круга – радиусом кривизны (в данной точке). Для радиуса
кривизны, очевидно, имеем формулу
1
R
k
(k кривизна кривой )
Кривизна плоской кривой
Если кривая задана в параметрической форме
x (t ),
y (t ),
то координаты центра кривизны кривой в точке (x,y) равны
[ ' (t )]2 [ ' (t )]2
' (t ),
ξ x
' (t ) ' ' (t ) ' ' (t ) ' (t )
2
2
[
'
(
t
)]
[
'
(
t
)]
y
' (t ).
' (t ) ' ' (t ) ' ' (t ) ' (t )
Кривизна плоской кривой
Если кривая задана как график явной функции
y f (x),
то параметрическое уравнение этой кривой имеет вид
x t,
y f (t ).
Задача. Показать, что кривизна такой кривой
f ' ' ( x)
k
,
2 3/ 2
(1 [ f ' ( x)] )
а координаты центра кривизны
1 [ f ' ( x)]2
1 [ f ' ( x)]2
ξ x
f ' ( x), y
.
f ' ' ( x)
f ' ' ( x)
Эволюта плоской кривой
Геометрическое множество центров кривизны данной кривой
называется ее эволютой. Сама кривая по отношению к своей
эволюте называется эвольвентой.
Пример. Найти эволюту параболы y2=2px.
Дифференцируя уравнение, находим
2 yy ' 2 p; yy ' p,
( y ' ) 2 yy ' ' 0; yy ' ' ( y ' ) 2 ; y 3 y ' ' ( yy ' ) 2 ; y 3 y ' ' p 2 .
Координаты центра кривизны
1 [ y ' ]2
(1 [ y ' ]2 ) y 2
y2 p2
2 px p 2
3y2
ξ x
y' x
yy ' ( x) x
x
3x p
p,
y' '
y' ' y 3
p
p
2p
1 [ y ' ]2
(1 [ y ' ]2 ) y 2
y2 p2
y2
y
y
y y
y 2.
y' '
y' ' y 3
p2
p
Эволюта плоской кривой
Из полученных уравнений
3y2
y2
ξ
p, 2 .
2p
p
Исключаем y и получаем уравнение эволюты
2
8
(ξ p ) 3
27 p
(полукубическая парабола)
Метод итераций (последовательных приближений)
x ( x)
Замечание.
f ( x ) 0 x x cf ( x ) x ( x ) ( ( x ) x cf ( x ))
x1 ( x0 )
x2 ( x1 )
xn ( xn 1 )
Метод итераций
Принцип сжимающих отображений
Пусть выполнены следующие условия
(1) x [a, b] ( x ) [a, b],
(2) q (0,1) x, y [a, b] | ( x ) ( y ) | q | x y | .
Тогда на отрезке [a,b] существует и притом единственное
решение уравнения
x ( x ).
При этом метод итераций для x0∊[a,b] дает последовательность,
сходящуюся к решению этого уравнения. Более того
qn
| xn x |
| ( x0 ) x0 | .
1 q
Метод итераций
Доказательство. В силу условия (1) последовательность итераций
определена. Покажем, что она фундаментальна.
Лемма. При m≥n
| xm xn | q n | xm n x0 |
В самом деле
| xm xn || ( xm1 ) ( xn 1 ) | q | xm1 xn 1 |
Применяя при m≥n полученное неравенство n раз, получаем
| xm xn | q | xm1 xn 1 | q 2 | xm2 xn 2 | ... q n | xmn x0 |
Следствие:
| xn 1 xn | q n | x1 x0 |
Метод итераций
Оценим, теперь, величину
| xk x0 || ( xk xk 1 ) ( xk 1 xk 2 ) ... ( x1 x0 ) |
q k 1 | x1 x0 | q k 2 | x1 x0 | ... | x1 x0 |
k
1
q
| x1 x0 |
k 1
k 2
( q q ... 1) | x1 x0 |
| x1 x0 |
.
1 q
1 q
Итак, мы имеем два неравенства
| x1 x0 |
| xm xn | q | xmn x0 |, | xk x0 |
,
1 q
n
Из которых следует, что при m≥n
| x1 x0 |
| xm xn | q
1 q
n
Метод итераций
| x1 x0 |
| xm xn | q
(m n)
1 q
n
ε0
| x1 x0 |
n | x1 x0 |
lim q
0 N n N q
n
1 q
1 q
n
n N , m n | xm xn |
m, n N | xm xn |
Метод итераций
x lim xn
n
(1) a xn b x [a, b]
(2) 0 | ( xn ) ( x ) | q | xn x | ( xn ) ( x)
(3) xn ( xn 1 ) x ( x )
| x1 x0 |
n | x1 x0 |
| xm xn | q
, m | x xn | q
1 q
1 q
| x xn || xn x |, | x1 x0 || ( x0 ) x0 |
n
qn
| xn x |
| ( x0 ) x0 |
1 q
Метод итераций
Единственность решения.
x ( x ), y ( y )
| x y || ( x ) ( y ) | q | x y |
(1 q) | x y | 0
| x y | 0
x y
Иоганн Кеплер
Немецкий математик, астроном и оптик,
27.12.1571 – 15.11.1630 первооткрыватель законов движения планет
Солнечной системы.
В 1591 поступил в университет в Тюбингене, в
1594 приглашен для чтения лекций по
математике в университет города Граца
(Австрия).
На протяжении нескольких лет Кеплер в
результате тщательного анализа приходит к
выводу, что траектория движения Марса
представляет собой не круг, а эллипс, в одном из
фокусов
которого
находится
Солнце
—
положение, известное сегодня как первый закон
Кеплера.
Дальнейший анализ привёл ко второму закону: радиус-вектор,
соединяющий планету и Солнце, в равное время описывает равные
площади. Это означало, что чем дальше планета от Солнца, тем
медленнее она движется.
Иоганн Кеплер
В 1612 году Кеплер переезжает в Линц, где прожил 14 лет. За ним
сохранена должность придворного математика и астронома, но в деле
оплаты новый император ничем не лучше старого. Некоторый доход
приносят преподавание математики и гороскопы.
Продолжая астрономические исследования, Кеплер в 1618 году
открывает третий закон: отношение куба среднего удаления планеты от
Солнца к квадрату периода обращения её вокруг Солнца есть величина
постоянная для всех планет: a³/T² = const. Этот результат Кеплер
публикует в завершающей книге «Гармония мира», причём применяет его
уже не только к Марсу, но и ко всем прочим планетам, включая,
естественно, и Землю.
В 1626 году в ходе Тридцатилетней войны Линц осаждён и вскоре
захвачен. Начинаются грабежи и пожары. Кеплер переезжает в Ульм.
В 1630 году отправляется к императору в Регенсбург, чтобы получить
хотя бы часть жалованья. По дороге сильно простужается и вскоре
умирает.
Законы планетной кинематики, открытые Кеплером, послужили позже
Ньютону основой для создания теории тяготения. Ньютон математически
доказал, что все законы Кеплера являются следствиями закона тяготения.
Эллипс
y
r1 r2 2a
b
b a 2 c2
r1
c
r2
c
x
a
x2 y2
2 1 ( a b)
2
a
b
a большая полуось
b малая полуось
x2 y 2 a2
c
ε эксцентриситет
a
Уравнение Кеплера
истинная аномалия
x эксцентрическая аномалия
T период обращения
μ m1 m2
x
апоцентр
линия апсид
фокус
перицентр
2
T
g
a3
(среднее движение)
t время движения от перицентра
m t средняя аномалия
m x εsin x
Метод итераций (пример)
Уравнение Кеплера
x m ε sin x (0 ε 1)
( x ) m ε sin x
[a , b] [m 1, m 1]
'( x ) ε cos x | '( x ) | ε
| ( x ) ( y )|=| '(ξ)( x y )| ε|( x y )|
Таким образом, итерации
xn m ε sin xn 1
сходятся к единственному решению этого уравнения.
Метод итераций (пример)
Оценка погрешности:
1619
εn
| xn x |
| ( x0 ) x0 | .
1 ε
x 2 0,1sin x (с точностью до 0,001)
(0,1)n
m 2 ε 0,1 d
| ( x0 ) x0 |
0,9
x0 2,
d 0,1
x1 2,09093, d 0,01
x2 2,08678, d 0,001
x3 2,08698, d 0,0001
Ответ:
x 2,087
Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ.
Приближенные методы
решения уравнений.
Лекция 13
завершена.
Спасибо за внимание!
Тема следующей лекции:
Обзорная лекция.
Лекция состоится в четверг 18 декабря
В 10:00 по Московскому времени.