Лекция 6 Модели систем обслуживания 1
advertisement

Лекция 6
Модели систем обслуживания
1
Вопросы лекции
1.
2.
Модель обслуживания с потерями
Модель обслуживания с ожиданием
2
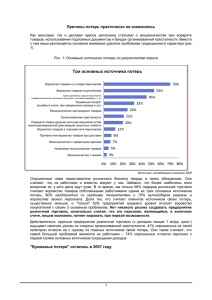
В 4 квартале 2011 г. компания Eriсsson провела международный
независимый аудит ключевых показателей производительности Network
Quality Benchmarking GSM Radio Network Report 2011, Q4.
Были оценены 79 операторов со всего мира, сети которых построены с
использованием оборудования компании Ericsson, и которые дали свое
согласие на обнародование результатов.
В результате «Киевстар» входит в 25% лучших сетей мира по
следующим показателям (cм. письмо из Ericcson с результатами
исследования):
· Доля голосовых вызовов с высоким качеством передачи голоса (Good
Speech Quality) — более 96%.
· Доля обрывов звонков — меньше чем 1 раз в 330 минут.
· Средняя скорость передачи данных от базовой станции к клиентскому
оборудованию по технологии EDGE — примерно 135 Кбит/с.
·
Объем трафика пакетных данных возрастает примерно на 5%
ежемесячно.
3
Модели обслуживания
Теория массового обслуживания – раздел
математики, который включает в себя математический
аппарат описания процессов обслуживания в любых
системах, где есть поступающий поток заявок на
обслуживание и, как правило, ограниченный ресурс по
обслуживанию ( АЗС, парикмахерская, склад, аэродром,
АТС и др.).
Основная цель использования инструментов ТМО определение ( расчет) оптимального соотношения между
количеством обслуживающих приборов в системе,
входным потоком заявок и требованиями к качеству их
обслуживания.
4
Модель обслуживания с потерями
Модель системы обслуживания с потерями (отказами)
отражает процесс обслуживания заявок при следующих
предположениях:
система имеет v полнодоступных обслуживающих приборов
время обслуживания вызова – случайная величина t,
распределенная по показательному закону. Причем,
среднее значение
_
t 1
дисциплина обслуживания – с явными потерями вызовов изза занятости всех обслуживающих приборов в момент их
поступления
число занятых приборов i={1,v} – это i-ое состояние
системы
параметр входного потока λi отражает интенсивность
поступающего потока в во время нахождения системы в i-ом
состоянии
5
Модель обслуживания с потерями
система меняет скачкообразно свое состояние
при поступлении вызова : i → i+1
при завершении обслуживания: i → i-1
Задача моделирования процесса работы системы:
Необходимо определить распределение вероятностей Рi(t)
нахождения системы в i-ом состоянии в момент времени t.
Возможные переходы между состояниями системы описывает
цепь Маркова
pi1,i(t)
i-1
i
i+1
pi+1,i(t)
Графическое
представление
цепи Маркова
Pi (t ) Pi 1 (t t ) pi 1,i (t ) Pi (t t ) pi ,i (t ) Pi 1 (t t ) pi 1,i (t ) o(t )
6
Модель обслуживания с потерями
pi1,i(t)
i1
i-1
i
i
i+1
pi+1,i(t)
Вероятность нахождения системы в i -ом состоянии или нахождении в
системе i заявок в момент времени t
Pi (t ) Pi 1 (t t ) pi 1,i (t ) Pi (t t ) pi ,i (t ) Pi 1 (t t ) pi 1,i (t ) o(t )
Условные вероятности переходов между состояниями определяются в виде
pi 1,i (t ) i 1t o(t )
pi 1,i (t ) i 1t o(t ) (i 1)t o(t )
(i 1)t
_
t
o(t ) (i 1)t o(t )
7
Модель обслуживания с потерями
pi,i(Δt) определяется из уравнения
pi ,i (t ) pi 1,i (t ) pi 1,i (t ) o(t ) 1
pi ,i (t ) 1 pi 1,i (t ) pi 1,i (t ) o(t )
pi ,i (t ) 1 i 1t it o(t )
8
Модель обслуживания с потерями
Вероятность нахождения системы в i-ом состоянии в произвольный
момент времени
Pi (t ) i1tPi1 (t t ) (i 1)tPi1 (t t ) (1 i t it ) Pi (t t ) o(t )
При Δt →0 для установившегося режима t→∞ линейная система
уравнений имеет вид
(i i) Pi i 1Pi 1 (i 1) Pi 1
(i 1) Pi 1 i Pi
_________
i 0, v 1
9
Модель обслуживания с потерями
При i=0 переход из состояния i-1 в состояние I не имеет места.
Поэтому
P1 0 P0
В итоге можно получить
i 1
Pi
k
k!
k 0
v j 1
j 0 k 0
k
______
i 0, v
j!
10
Модель обслуживания с потерями
При условии отсутствия потерь v →∞ для простейшего
поступающего потока из распределения Эрланга получается
распределение Пуассона
i
Pi
i!
j 0
j
i
i!
e
j!
Система обслуживания без потерь формирует простейший
выходной (исполненный) поток
11
Модель обслуживания с потерями
Распределение Эрланга является очень важным соотношением
для оценки показателей потерь в системе обслуживания с
потерями ( отказами из-за занятости всех обслуживающих
приборов)
В предположении t = 1 параметр поступающего потока численно
равен интенсивности поступающей нагрузки
λ*t = A или A = λ
Вероятность занятия всех v устройств pv равна вероятности потери р
вызова
Av
v!
p
v
Aj
j!
j 0
1 формула
Эрланга
Формулой Эрланга пользуются для расчета соотношения между p, A, v
12
Модель обслуживания с потерями
Таблицы Эрланга
A
Значения в таблице
– потери вызовов р
Number of devices n
1
.333333
.354839
.375000
.393939
.411765
.428571
.444444
.459459
.473684
.487180
.500000
.512195
.523810
.534884
.545455
0.50
0.55
0.60
0.65
0.70
0.75
0.80
0.85
0.90
0.95
1.00
1.05
1.10
1.15
1.20
2
.076923
.088905
.101124
.113499
.125964
.138462
.150943
.163369
.175705
.187923
.200000
.211917
.223660
.235216
.246575
3
.012658
.016038
.019824
.024001
.028552
.033457
.038694
.044240
.050072
.056167
.062500
.069050
.075793
.082709
.089776
4
.001580
.002200
.002965
.003885
.004972
.006234
.007679
.009313
.011141
.013164
.015385
.017803
.020418
.023226
.026226
n
Значения в таблице
– нагрузка А
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5
.000158
.000242
.000356
.000505
.000696
.000934
.001227
.001581
.002001
.002495
.003067
.003725
.004472
.005314
.006255
6
.000013
.000022
.000036
.000055
.000081
.000117
.000164
.000224
.000300
.000395
.000511
.000651
.000819
.001017
.001249
A
7
.000001
.000002
.000003
.000005
.000008
.000013
.000019
.000027
.000039
.000054
.000073
.000098
.000129
.000167
.000214
8
.000001
.000001
.000002
.000003
.000004
.000006
.000009
.000013
.000018
.000024
.000032
9
.000001
.000001
.000001
.000002
.000003
.000004
10
0.50
0.55
0.60
0.65
0.70
0.75
0.80
0.85
0.90
0.95
1.00
1.05
1.10
1.15
.000001 1.20
Loss probability (E)
0.007
.00705
.12600
.39664
.77729
1.2362
1.7531
2.3149
2.9125
3.5395
4.1911
4.8637
5.5543
6.2607
6.9811
7.7139
0.008
.00806
.13532
.41757
.81029
1.2810
1.8093
2.3820
2.9902
3.6274
4.2889
4.9709
5.6708
6.3863
7.1155
7.8568
0.009
.00908
.14416
.43711
.84085
1.3223
1.8610
2.4437
3.0615
3.7080
4.3784
5.0691
5.7774
6.5011
7.2382
7.9874
0.01
.01010
.15259
.45549
.86942
1.3608
1.9090
2.5009
3.1276
3.7825
4.4612
5.1599
5.8760
6.6072
7.3517
8.1080
0.02
.02041
.22347
.60221
1.0923
1.6571
2.2759
2.9354
3.6271
4.3447
5.0840
5.8415
6.6147
7.4015
8.2003
9.0096
0.03
.03093
.28155
.71513
1.2589
1.8752
2.5431
3.2497
3.9865
4.7479
5.5294
6.3280
7.1410
7.9667
8.8035
9.6500
n
0.05
.05263
.38132
.89940
1.5246
2.2185
2.9603
3.7378
4.5430
5.3702
6.2157
7.0764
7.9501
8.8349
9.7295
10.633
0.1
.11111
.59543
1.2708
2.0454
2.8811
3.7584
4.6662
5.5971
6.5464
7.5106
8.4871
9.4740
10.470
11.473
12.484
0.2
.25000
1.0000
1.9299
2.9452
4.0104
5.1086
6.2302
7.3692
8.5217
9.6850
10.857
12.036
13.222
14.413
15.608
0.4
.66667
2.0000
3.4798
5.0210
6.5955
8.1907
9.7998
11.419
13.045
14.677
16.314
17.954
19.598
21.243
22.891
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13
Модель обслуживания с потерями
Графики функции Эрланга
A
Для упрощения расчетов иногда применяется линейная интерполяция
экспоненциальных кривых функций
Например,
Для Р = 1%
V = 5,5 + 1,17 × А
Для Р = 0,1%
V = 7,8 + 1,28 × А
14
Модель обслуживания с потерями
Для примитивного потока вызовов с параметром λi=a(Ni) в
системе с потерями получается распределение Энгсета ( N > v)
Pi
C Ni a i
v
j
j
C
a
N
j 0
Для примитивного потока вызовов с параметром λi=a(Ni) в
системе без потерь с учетом бинома Ньютона
N
j j N j
N
C
a
b
(
a
b
)
N
j 0
получается распределение Бернулли ( N = v)
Pi
C Ni a i
v
j
j
C
a
N
j 0
C Ni a i
(1 a ) N
15
Модель обслуживания с потерями
По-сути, вероятность занятости прибора равна вероятности
нахождении источника в активном соcтоянии
a
a
1 a
Поток вызовов от одного источника
1
2
t cв1
3
n-1
n
t cв2
t зан1
t
t cвn
t зан2
t зан3
t занn-1
t занn
Интенсивность или активность источника в свободном состоянии a – это
отношение числа поступивших вызовов к суммарному свободному
времени
n
n
1
1
a n
a n
n
__
tcвi
tсс
tcв
tcв
i 1
i 1
i
i 1
n
i
16
Модель обслуживания с потерями
Поток создается только свободными источниками. Поэтому
параметр потока зависит от состояния каждого источника
Состояния источника - свободен/занят как временной процесс
Поток вызовов от одного источника
1
2
t cв1
3
n-1
t
n
t cв2
t cвn
t зан1
t зан2
t зан3
t занn-1
t занn
Интенсивность или активность источника в свободном состоянии a – это
отношение числа поступивших вызовов к суммарному свободному
времени
a
n
a
n
tcв
i 1
i
n
n
tcв
i 1
i
1
n
tcв
i
i 1
n
1
__
tсс
17
Модель обслуживания с потерями
При известном показатели активности источника
получается распределение Бернулли вероятностей
активности N источников
Pi C Ni a i (1 a ) N i
Для простейшего потока вызовов с параметром λ
для системы с потерями получаем первое
распределение Эрланга
i
Pi
i!
v
j 0
j
j!
18
Модель обслуживания с ожиданием
Модель системы обслуживания с ожиданием отражает
процесс обслуживания заявок при наличии мест ожидания в
очереди и при следующих предположениях:
система имеет v полнодоступных обслуживающих приборов
в состоянии i= { 0;v } в системе занято ровно i приборов
в состоянии i= { v;∞ } в системе есть очередь длиной i-v
время обслуживания вызова – случайная величина t,
распределенная по показательному закону. Причем,
среднее значение
_
t 1
параметр входного потока λi отражает интенсивность
поступающего потока в во время нахождения системы в i-ом
состоянии
19
Модель обслуживания с ожиданием
Распределение вероятностей Рi нахождения в системе в i-ом состоянии
имеет вид
i
Pi
v 1
j 0
Pi
v 1
j 0
_____
i!
j! (v )(v 1)!
j
j
v
v
i v
i 0, v
v
v!
v
j! (v )(v 1)!
_______
i v,
Это распределение называется вторым распределением Эрланга
20
Модель обслуживания с ожиданием
Вероятность ожидания поступившего вызова
P (tожид
v
(v )(v 1)!
0) Pk v 1 j
v
k v
(v )(v 1)!
j 0 j!
2 формула
Эрланга
Интенсивность обслуженной нагрузки
Y=λ
Все заявки ожидают обслуживание, поэтому отсутcтвие
потерь обуславливает численное равенство интенсивностей
обслуженной и поступающей нагрузок
Y=A
21
Модель обслуживания с ожиданием
Вероятность превышения длины очереди
заданной величины n
v
n 1
(v )(v 1)!
P ( S n) Pi v 1 j
v
v
i v n 1
(v )(v 1)!
j 0 j!
Средняя длина очереди
Y=λ
v
__
(v )(v 1)!
P ( S ) (i v) Pi iPi v
v 1 j
v
v
i v
i 0
(v )(v 1)!
j 0 j!
22
Модель обслуживания с ожиданием
Средняя длительность ожидания
_______
tожид
1
P(tожид
v
v
(v )(v 1)!
1
0)
v 1 j
v
v
(v )(v 1)!
j 0 j!
Вероятность ожидания свыше времени tq ( за время tq
освободились не более i-v приборов/линий). Параметр
потока освобождений постоянный и равен v
i v
i v
k 0
k 0
P (tожид t q ) Pk (t q )
k
vtq vt q
e
k
23
Модель обслуживания с ожиданием
Дальнейшим развитием моделей обслуживания с
ожиданием являются
Модели обслуживания с постоянным временем
ожидания ( фиксированная длина пакетов)
Модели с повторным поступлением заявок на
обслуживание при занятости всех обслуживающих
приборов
Модели обслуживания с приоритетами ( категорийное
обслуживание)
В этих моделях невозможно точно описать функцию
распределения вероятностей. Поэтому в них
определяются некоторые показатели при возможных
допущениях
24
Литература
Романов А. И. Телекоммуникационные сети и управление: Учебное
пособие –К. ИПЦ « Киевский университет», 2003, -247с.
Корнышев Ю.Н., Фань Г.Л. Теория распределения информации – М.:
Радио и связь, 1985
Сети ЭВМ. Под редакцией В.М. Глушкова – М.: Связь, 1977
Бусленко Н. П. Моделирование сложных систем – М. : Наука, 1978
Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового
обслуживания – М.: Наука, 1966
Клейнрок Л. Коммутационные сети – М.: Наука, 1970
Шварц М. Сети ЭВМ. Анализ и проектирование - М.: Радио и связь,
1981
Советов Б.Я. и др. Построение сетей интегрального обслуживания –
Л.: Машиностроение, Лен отд-е, 1990
Клейнрок Л. Вычислительные сети с очередями – М.: Мир, 1979
Хилс М.Т. Принципы коммутации в электросвязи - М.: Радио и связь,
1984
Френк Г. , Фриш И. Сети, связь и потоки – М.: Связь, 1978
25
Спасибо за внимание!
26