Потоки в сетях
advertisement
Потоки в сетях.
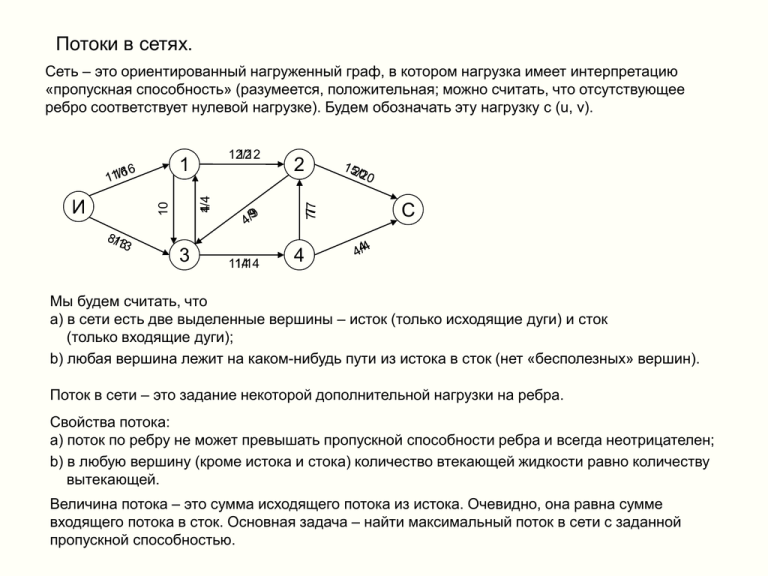
Сеть – это ориентированный нагруженный граф, в котором нагрузка имеет интерпретацию
«пропускная способность» (разумеется, положительная; можно считать, что отсутствующее
ребро соответствует нулевой нагрузке). Будем обозначать эту нагрузку c (u, v).
12/12
12
3
7
7/7
10
И
2
1/4
4
1
11/14
14
С
4
Мы будем считать, что
a) в сети есть две выделенные вершины – исток (только исходящие дуги) и сток
(только входящие дуги);
b) любая вершина лежит на каком-нибудь пути из истока в сток (нет «бесполезных» вершин).
Поток в сети – это задание некоторой дополнительной нагрузки на ребра.
Свойства потока:
a) поток по ребру не может превышать пропускной способности ребра и всегда неотрицателен;
b) в любую вершину (кроме истока и стока) количество втекающей жидкости равно количеству
вытекающей.
Величина потока – это сумма исходящего потока из истока. Очевидно, она равна сумме
входящего потока в сток. Основная задача – найти максимальный поток в сети с заданной
пропускной способностью.
Потоки в сетях.
Пусть задана сеть и поток в ней. Свяжем с потоком функцию f (u, v), обладающую следующими
свойствами:
12/12
3
7/7
10
И
2
1/4
1
11/14
С
4
a) если по ребру (u,v) идет поток величиной c, то положим f (u, v) = c, f (v, u) = -c;
b) если есть два «встречных» потока c1 и c2 по ребрам (u, v) и (v, u) соответственно, то
полагаем f (u, v) = c1-c2. На самом деле всегда можно считать, что на самом деле есть
только один поток величиной |c1-c2|.
На приведенной выше картинке: f (И, 3) = 8; f (3, 2) = -4; f (1, 3) = -1.
Для каждого ребра (при заданном потоке f) определим также его «остаточную пропускную
способность»: cf(u, v) = c (u, v) – f(u, v)
Например, для заданного потока cf(3, 4) = 3, cf(1, 3) = 11.
Метод Форда – Фалкерсона
Будем искать дополняющие пути из истока в сток, по которому можно пропустить
дополнительное количество вещества. Тогда схема алгоритма может быть записана
следующим образом:
f = 0;
while (существует дополняющий путь p) {
дополнить f вдоль p;
}
Для поиска дополняющих путей найдем все остаточные пропускные способности ребер сети
и составим остаточную сеть из всех положительных величин:
3
11
12/12
1
И
2
3
11/14
4
С
2
7
3
11
3
7/7
11/14
4
10
3
И
С
7/7
1/4
10
И
12
1
2
1/4
12/12
1
4
С
Пример реализации метода Форда – Фалкерсона
7/14
10
12
1
С
И
4
7
4
14
7
3
С
4
2
7
3
3
2
4
10
И
4
7/7
12/12
1
И
С
7
14
С
2
4
3
12
1
7
4
10
И
2
10
12/12
12
1
С
4
7
2
3
11/14
4
12
1
И
2
4
С
10
4
И
10
1
7/7
12/12
3
3
11
4
Выбор дополняющего пути в методе Форда – Фалкерсона
Если выбор дополняющего пути производится не очень удачно, то процедура поиска
максимального потока может затянуться.
1/1
1
И
С
И
1
1
1
С
2
2
1
С
1
И
и так далее, всего 2 000 000 шагов…
2
Можно попробовать искать кратчайший (по числу ребер) дополняющий путь между истоком
и стоком. Например, с помощью поиска в ширину. Получающийся при этом алгоритм
(реализация метода Форда – Фалкерсона) называется алгоритмом Эдмондса – Карпа).
Можно показать, что в алгоритме Эдмондса – Карпа число шагов ограничено сверху числом
2nm, где m – число ребер в сети, а n – число вершин. Поскольку поиск в ширину, изменение
потоков вдоль ребер и построение остаточной сети требуют времени O(m), то общее время
работы алгоритма можно оценить как O(m2n).
Сеть с несколькими истоками и стоками
Если в графе есть несколько истоков и/или несколько стоков, то задача нахождения
максимального потока в такой сети сводится к задаче с одним истоком и одним стоком.
И2
3
И3
С1
С
6
12
∞
4
И
11
2
5
4
9
И1
10
1
7
С2
Максимальное паросочетание в двудольном графе
Метод Форда – Фалкерсона можно использовать и для решения других задач, например, для
поиска максимального паросочетания в двудольном графе.
a1
b1
a2
Максимальное паросочетание – это паросочетание
с наибольшим числом ребер.
b2
a3
b3
a4
b4
a5
Паросочетание – это множество ребер в двудольном
графе, при котором каждая вершина
связана не более, чем с одним ребром из этого
множества.
Применение метода Форда – Фалкерсона для нахождения максимального
паросочетания
Добавим в граф две вершины – исток и сток – так, как показано на рисунке. Пропускную
способность всех ребер полагаем равной единице. Тогда максимальный поток определит
максимальное паросочетание в этом графе.
a1
b1
a2
b2
И
С
a3
b3
a4
b4
a5
Проталкивание предпотока для нахождения максимального потока
Сначала исток поднимается на высоту, равную общему числу вершин, и в соседние с ним
вершины заливается максимальное количество жидкости.
Вершина, в которой есть избыток жидкости, поднимается на минимально возможную высоту,
с которой можно слить жидкость в одну из соседних вершин по остаточной сети.
Жидкость сливается по одному из возможных ребер остаточной сети.
И так далее...
Работа алгоритма прекращается, когда в сети не остается больше «избыточных» вершин.
В процессе работы жидкость может возвращаться назад к истоку, уменьшая общую начальную
величину потока.
6
5
4
3
2
13
1
4
16
0
И
16
12/12
12
3/10
10
10
4/10
10
10
12
4
4
9
13
17
26
77
14
4
3
С
Реализация алгоритма проталкивания предпотока
for (int i = 0; i < n; ++i) {
h[i] = 0; e[i] = 0;
}
h[s] = n;
for (Arc arc : arcs) {
int u = arc.start; v = arc.end;
f[u,v] = f[v,u] = 0;
}
for (int u : adj(s)) {
f[s,u] = c[s,u];
f[u,s] = -c[s,u];
e[u]
= c[s,u];
}
while (есть избыточные вершины) {
for (int u : excs) {
if (возможно проталкивание избытка)
протолкнуть избыток;
else
поднять вершину;
}
}
Никакая вершина не может быть поднята на высоту, большую или равную 2n. Поэтому общее
число операций подъема не может быть больше 2n2.
Можно показать, что общее число операций оценивается как O(n2m), что лучше, чем в алгоритме
Эдмондса – Карпа (O(nm2)).










