Лекция 11 Движение в поле гравитации
advertisement

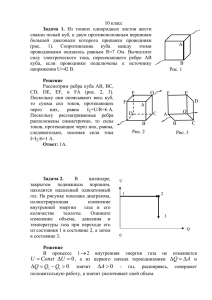
Лекция 11 Движение в поле гравитации Закон всемирного тяготения. Экспериментальное определение постоянной гравитации. Гравитационное поле, его характеристики. Задача Кеплера. Гравитационная энергия однородного шара. Гравитационный радиус. Гравитационное красное смещение. Закон всемирного тяготения. На основе наблюдательных данных Кеплер (1571-1630) установил законы движения планет Солнечной системы: - каждая планета движется по эллиптической орбите, в одном из фокусов которого находится Солнце; - радиус-вектор планеты в равные времена описывает равные площади; - квадраты периодов обращений планет относятся как кубы больших осей соответствующих эллиптических орбит. Используя эти законы, Ньютон установил закон всемирного тяготения, согласно которому любые два тела (частицы) массами m1 и m2 в вакууме притягиваются друг к другу с центральными силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними: F12 G m1m2 r12 , r122 G 6,67 108 дин см2 / г 2 – одна из фундаментальных постоянных, ной гравитации, r12 - расстояние между частицами (рис.11.1). где (11.1) называемая постоян- Рис. 11.1 Эти силы называются гравитационными силами, или силами всемирного тяготения. Экспериментальное определение постоянной гравитации. Опыт Кавендиша (1731-1810). Первое непосредственное доказательство закона (11.1) в лабораторных условиях и численное определение постоянной гравитации были проведены Кавендишем в 1798г. на крутильных весах (рис.11.2). Вблизи концов коромысла, укрепленными одинаковыми шариками массы m, помещались два других больших свинцовых шара массы M каждый, m , сначала в положении AA , затем – BB . Из-за гравитационного притяжения шариков с шарами, коромысло поворачивался соответственно на углы 1 и 2 . причем M Рис. 11.2 Углы измерялись смещением луча света, отраженного от зеркала З (рис.11.2). В положениях и BB на коромысло действует крутящий момент пары гравитационных сил уравновешивается упругим моментом закрученной нити f 1 GMm / r 2 ; где - длина коромысла, r f : GMm / r 2 дуль кручения, который находят из периода крутильных колебаний коромысла m 2 2f . В результате для определения G получаем формулу G 2 r2 MT 2 , который f 2 GMm / r 2 , – расстояние между центрами шарика и ближайшего шара, T 2 AA (1 2 ), где фигурируют только измеряемые величины. Рис. 11.3 f - мо- Опыт Жолли (1809-1880). В этом методе используются рычажные весы, на левом плече которых подвешены две чашки, как это показано на рис.11.3. Между чашками неподвижно установлен тяжелый свинцовый шар с узким вертикальным каналом, сквозь который проходит нить, соединяющая чашки. Если на верхнюю чашку положить шарик массы m, то на него будет действовать вниз сила F1 mg GMm / r 2 , где r - расстояние между центрами шарика и тяжелого шара. Ес- ли шарик перевести на нижнюю чашку, то на него будет действовать сила F2 mg GMm / r 2 . Следовательно, для восстановления равновесия рычажных весов после перемещения шарика в нижнее положение, надо уменьшить груз на правом плече чашки весов на откуда и можно найти значение F1 F2 2GMm / r 2 , G. Гравитационное поле. Согласно современным представлениям тяготение между телами осуществляется, так называемыми гравитационным полем. Каждое тело создает в окружающем пространстве силовое поле, которое и действует на тела в этой области. Силовой характеристикой этого поля служит его напряженность – сила, действующая на единицу массы пробной частицы массой в точке r поля: g r F / m . m , помещенной (11.2) Это – не что иное, как ускорение свободного падения частицы в данной точке. Для поля точечной массы m оно, с помощью (11.1), (11.2) выразится формулой g (r ) Gm r. r2 (11.3) Энергетической характеристикой гравитационного поля служит его потенциал. Это гравитационный потенциал единицы массы пробной частицы: r U r / m . (11.4) Для поля точечной частицы массы m имеем r Gm / r . (13.5) Принцип независимости действия сил для полей приводит к принципу их суперпозиции: гравитационное поле, создаваемое несколькими телами, равно геометрической сумме гравитационных полей, возбуждаемых этими телами в отдельности. Математически этот принцип выражается формулами g r gi r , r i r . (11.6) На основе этих формул можно вычислить гравитационное поле любого тела. Для этого надо мысленно разбить тело на малые части, и подсчитать характеристики поля по формулам (11.3), (11.5) и (11.6). Пользуясь принципом суперпозиции, можно показать (см. задачи), что внешние гравитационные поля однородного шара и шаровой оболочки, выражаются формулами (11.3) и (11.5), и поэтому два однородных шара (сферические оболочки) притягиваются между собой так, как если бы их массы были сконцентрированы в их центрах. Задача Кеплера. Рассмотрим теперь движение легкой частицы массы m в поле гравитации тяжелой точечной m , (задача Кеплера). Эта задача, фактически, достаточно хорошо моделирует двимассы M жения планет в поле гравитации Солнца. Понятно, что в зависимости от меры сообщаемой частице энергии Е, ее движение в поле гравитации точечной массы будет либо финитным (эллипс), либо инфинитным (парабола, или гипербола). Поэтому, задача сводится к нахождению условий финитности, или инфинитности движения частицы. Так как диссипативные силы отсутствуют, то энергия частицы сохраняется 2 mv 2 GMm mvr2 mv GMm E const , 2 r 2 2 r где vr , v – радиальная и азимутальная компоненты скорости, r (11.7) – расстояние частицы до точеч- ной массы. Используя закон сохранения момента импульса частицы: L mrv const , (11.8) и исключая его помощью азимутальную скорость из (11.7), получим E mvr2 / 2 GMm / r L2 / 2mr 2 . (11.9) Формально это выражение можно рассматривать как энергию одномерно-радиального движения частицы во внешнем поле с эффективным потенциалом U эфф GMm / r L2 / 2mr 2 , (11.10) зависимость которого от силового центра r схематически представлена на рис.11.4. рис. 11.4 Так как первый член правой части (11.9) неотрицательная величина, то область пространства, U эфф E . Проведем горизонтальную прямую E const . Области пространства, соответствующие участкам кривой U эфф , которые лежат выше этой прямой, не достигаемы частицей с энергией E (рис.11.5). в которой может находиться частица, определится условием Рис.11.5 Если E 0 , то прямая E const пересекает кривую рым соответствуют расстояния от центра rmin r rmax , rmin и rmax . U эфф (r ) в двух точках поворота, кото- Движение частицы локализовано в области т.е. финитно, и соответствует движению по эллипсу. Расстояния rmin и rmax , ко- торые называются перицентром и апоцентром эллиптической орбиты, являются решениями уравнения U эфф E : r 2 GMm / E r L2 / 2mE 0 . (11.11) Введя эксцентриситет траектории как e rmax rmin / rmax rmin , и пользуясь теоремой Виета: rmin rmax GMm / E, rmin rmax L2 / 2mE , (11.12) получим следующую формулу e2 1 2EL2 / G 2 M 2 m3 , (11.13) которая дает связь формы траектории частицы с параметрами задачи. Минимуму эффективного потенциала соответствует расстояние от центра энергия E0 m GMm / L / 2 2 (их легко получить из (11.10)). Подставляя дим соответствующее значение эксцентриситета r0 L2 / GMm2 E0 и в (11.13), нахо- e 0 . Это круговое движение с радиусом ор- биты r0 . Из (11.8) для скорости кругового движения получаем vк L / mr0 GMm / L GM / r0 1 2 . (11.14) rmax r0 (круговое движение), то получитE U K , то для кругового движения получаем Если в первое соотношение (13.12) положить rmin 2 E GMm / r0 , или 2E U . И так как E K . Т.е. при круговом движении сумма ся полной и кинетической энергий частицы равна нулю. Уравнение (11.11) дает два вещественных корней лишь в области энергий ответствует эллиптическая орбита со значениями эксцентриситета 0 e 1 E0 E 0 . Им со(рис.11.6). рис. 11.6 Большая полуось эллипса имеет длину b a 1 e2 Если 1 2 E 0, L / 2mE то прямая расстоянию от центра rmin . 1 2 a (rmin rmax ) / 2 GMm / 2 E , а малая полуось – . E const пересечет кривую только в одной точке, соответствующей Двигаясь к центру, частица остановится на расстоянии rmin и меняет направление радиальной скорости в обратную сторону, удаляясь в бесконечность. Это – инфинитное движение, а траектория – гипербола. Наконец, при E 0 , движение частицы также инфинитно – но с параболической траекторией (рис.11.7). Так как в бесконечном расстоянии от цен- U эфф 0 , то здесь E mv2 / 2 . Отсюда следует, что при гиперболическом движении частица приходит в бесконечность с конечной скоростью v , а при параболическом движении – с нулевой скоростью. Начальная скорость v п , которую надо сообщить частице на расстоянии r0 , чтотра бы она стала двигаться по параболе, называется параболической скоростью. Ее можно определить из (11.7), подставив в него E 0 : mvп2 / 2 GMm / r0 0 , откуда vп 2GM / r0 1 2 (11.15) рис. 11.7 Сравнивая (11.14) и (131.15), получим vп vк 2 . Полученные здесь формулы применимы к движениям тел в околоземном пространстве, где можно пренебречь сопротивлением атмосферы. В частности, применительно к Земле формулы (11.14) и (11.15) выражают первую (круговую) и вторую (параболическую) космические скорости. Именно такие скорости нужно сообщить телу на поверхности Земли (при этом r0 – радиус Земли), чтобы оно двигался вокруг нее по кругу, или по параболической орбите. Убедитесь сами, что приблизительные значения этих скоростей соответственно равны 8 км/с и 11,2 км/с. Собственная гравитационная энергия однородного шара. Тела, которые формировались и удерживаются внутренними силами всемирного тяготения, называются гравитирующими. Таковыми являются планеты, звезды и разнообразные совокупности звезд. Работу внутренних консервативных сил мы характеризовали собственной потенциальной энергией, которая в рассматриваемом случае называется гравитационной. Это – работа гравитационных сил при полном разрушении системы, т.е. при превращении системы в конфигурацию с нулевой гравитационной энергией. Это соответствует ситуации, когда расстояния между всеми частицами бесконечны. Рис. 11.8 Поэтому, разобьем мысленно шар радиуса R и массы M на бесконечно тонкие концентрические слои и последовательно удалим их в бесконечность. Пусть в этом процессе удаляем слой с массой dm из поверхности шара массы mr в бесконечность (рис.11.8). Так как в бесконечности по- тенциальная энергия слоя равна нулю, то изменение гравитационной энергии при этом перемещении будет - r dm , где r Gm r / r – гравитационный потенциал на поверхности шара. Гравитационную энергию шара получим, производя интегрирование: Gm GM 1/ 3 M 2 / 3 3 GM 2 U dm m dm M r R 0 5 R 0 где мы исключили из первого подынтегрального выражения ным соотношением для однородного шара: m / M r / R 3 , (11.16) r , пользуясь следующим очевид- . Знак минус вызван с выбором конфи- гурации с нулевой энергией (чтобы достичь ее следует сообщить шару положительную энергию). Заметим, что гравитационная энергия шара данной массы обратно пропорциональна его радиусу. Уменьшая радиус, т.е. уплотняя шар, можно его гравитационную энергию увеличить до энергии покоя - Mc 2 . Легко оценить, что это случится при радиусе Rg GM / c2 , (11.17) который называется гравитационным радиусом тела. Не трудно оценить, что для Солнца (M 2 1033 г , R 700000км ) он порядка километра, а для Земли ( M 6 1027 г, R 6400км ) – порядка метра, так что гравитационная энергия составляет лишь ничтожную долю от энергии их покоя. Совершенно иная ситуация у сверхплотных – нейтронных звезд (пульсары), которые при радиусе в 10 км имеют массы порядка солнечных(!). Легко убедиться, что плотность массы у них порядка плотности масс атомных ядер. Гравитационная энергия нейтронных звезд составляет 10% - 30% от энергии их покоя. Гравитационное поле вокруг таких сверхплотных образований уже не описываются простыми формулами (11.3),(11.5). Эйнштейн в 1915г. построил релятивистскую теорию гравитации, или общую теорию относительности, в рамках которой и описываются эти объекты и связанные с ними явления. Однако некоторые экзотические явления можно предварительно получить и в рамках Ньютонов теории гравитации с учетом выводов специальной теории относительности. Например, легко убедиться, что круговая скорость у поверхности (в действительности такая поверхность не может находиться в равновесии, а под действием мощных сил гравитации должна безудержно сжиматься к центру) объекта с радиусом (11.17) равна скорости света. Это означает, что световой квант не в состоянии преодолеть притяжение такого объекта и выйти наружу, т.е. их нельзя наблюдать непосредственно. Однако их можно обнаружить по определенным явлениям, если они входят в состав двойной звезды. Такие объекты носят название черных дыр. Гравитационное красное смещение. Световой квант, излучаемый гравитирующим телом (звездой), должен тратить определенную энергию для преодоления его гравитационное притяжение. Это – гравитационная энергия кванта света на поверхности тела. Поэтому, энергия преодолевшего притяжение тела светового кванта будет меньше, чем его энергия на поверхности тела. Следовательно, спектры принимаемых на Земле излучений звезд должны быть смещенными в сторону меньших частот (больших длин волн), т.е. в сторону красной границы спектра. Это и называется гравитационным красным смещением спектральных линий излучения звезд. рис.11.9 Для оценки красного смещения спектров излучения звезд рассмотрим световой квант частоты 0 на поверхности звезды массы M и радиуса R (рис.11.9). Полная энергия кванта на поверхности 2 звезды складывается из энергии h 0 и его потенциальной энергии m R , где m h 0 / c – масса фотона, а R GM / R – гравитационный потенциал звезды на ее поверхности. Энер- гия преодолевшего притяжение звезды и регистрируемого приемником фотона будет (рис.11.9). Применяя закон сохранения энергии к двум описанным состояниям фотона: h h h 0 GMh 0 / Rc 2 h 0 1 Rg / R , где пользовались формулой (11.17) для гравитационного радиуса, находим, что относительное смещение частоты отрицательно и равно v v0 / v0 Rg / R . Для обычных звезд отношение порядка 0,1-0,3. Rg / R мало – порядка 104 106 , (11.18) а для нейтронных звезд – Вообще, гравитационное красное смещение происходит, когда фотон перемещается в поле тяготения из точки с меньшим потенциалом в точку с большим потенциалом. Очевидно, при обратном перемещении получится фиолетовое смещение, т.е. частота фотона будет расти. Паунд и Ребекка в 1960г. регистрировали изменение частоты -излучения в лабораторных условиях при -кванта в вертикальном направлении всего в 22 м. Относительное изменение длиγ-кванта при этом составляло / 0 4,92 1015 . В этих опытах было получено перемещении ны волны / 0 5,13 0,51 1015 , что является блестящим подтверждением явления гравитационного смещения спектральных линий. Контрольные вопросы: ● Сформулируйте законы Кеплера. ● Для каких тел сформулирован закон всемирного тяготения? ● Какие физические параметры характеризуют гравитационное поле? ● Опишите опыты измерения постоянной гравитации. ● Каковы условия финитного (инфинитного) движения частицы в поле центральных сил? ● Выводите формулы космических скоростей. ● Выводите формулу собственной гравитационной энергии однородного шара. ● Что такое гравитационный радиус? ● Как можно с помощью спектра обнаружить гравитационное красное смещение? ● Каково физическое следствие от равенства инертной и гравитационной масс? Литература 1. Абрамян М.Г. Физические основы механики. Изд. ЕГУ, 1997 – 370 стр. (на армянском яз.). 2. Сивухин Д.В. Общий курс физики. Механика. М., Наука, 1979 – 520 стр. 3. Китель Ч., Найт У., Рудерман М. Берклеевский курс физики, том 1, Механика. М., Наука, 1975 -480 с. (БКФ, Механика). 4. Абрамян М.Г., Бадалян Э.С. Задачник по общему курсу физики. «Эдит-принт», 2002 – 220 стр. 5. Иродов И.Е. Задачи по общей физике. M., Наука, 1979; «Лань», 2001 – 416 стр. Задачи