fizika - BSUIR Helper
advertisement

1. Скорость. Путь. Пусть материальная точка совершает движение в
выбранной СО. Вектор, проведённый из начального положения точки в
конечное называется перемещением (Δ𝑟̅ ). Тогда векторная величина ⟨𝑣̅ ⟩ =
⟨𝑣̅ ⟩ =
Δ𝑟̅
Δ𝑡
называется средней скоростью перемещения. Длина участка
траектории, пройденного точкой за промежуток Δ𝑡, называется путёмS (𝑆 ≥
|Δ𝑟̅ |). Средняя скорость характеризует быстроту и направление движения
частиц. Среднюю быстроту движения тела по траектории характеризует
Δ𝑆
средняя путевая скорость⟨𝑣⟩ = Δ𝑡 . Как быстро и в каком направлении
движется тело в данный момент t характеризует мгновенная скорость𝑣̅ =
lim
Δ𝑟̅
Δ𝑡→0 Δ𝑡
′
̇ d𝑟̅. Мгновенная путевая скорость𝑣 = lim
= 𝑟̅ = 𝑟̅ =
d𝑡
Δ𝑆
Δ𝑡→0 Δ𝑡
|Δ𝑟̅ |следует, что |𝑣̅ | = lim
Δ𝑟̅
Δ𝑡→0 Δ𝑡
= lim
Δ𝑆
Δ𝑡→0 Δ𝑡
. При Δ𝑡 → 0, Δ𝑆 →
= 𝑣.Модуль мгновенной скорости 𝑣̅ равен
мгновенной путевой скорости 𝑣. Мгновенная скорость всегда направленна
по касательной к траектории. Для бесконечно малого перемещения 𝑑𝑟̅ =
𝑣̅ 𝑑𝑡. Для небольших промежутков Δ𝑟̅ = 𝑣̅ Δ𝑡 выполняется приближённо.
Скорость – векторная величина, значит, её можно записать в виде 𝑣̅ = 𝑣𝑥 𝑖̅ +
d𝑟̅
𝑑
𝑣𝑦 𝑗̅ + 𝑣𝑧 𝑘̅.
С
другой
стороны
𝑣 = d𝑡 = 𝑑𝑡 (𝑥𝑖̅ + 𝑦𝑗̅ + 𝑧𝑘̅) = 𝑥̇ 𝑖̅ + 𝑦̇ 𝑗 ̅ + 𝑧̇ 𝑘̅ .
Следовательно,
проекция
𝑑х
скорости
𝑣𝑥 = 𝑥̇ = 𝑑𝑡 …
Величина
(модуль)
скорости 𝑣 = √𝑣𝑥 2 + 𝑣𝑦 2 + 𝑣𝑧 2 .
𝑡
Пройденный путь частицы от 𝑡1 до 𝑡2 𝑆 = ∫𝑡 2 𝑣(𝑡)𝑑𝑡.
1
Ускорение. Нормальное и тангенциальное ускорения. При движении
материальной точки её скорость меняется как по величине, так и по
направлению. Как быстро это происходит в произвольный момент
времени, характеризует векторная величина ускорение. 𝑤 = lim
Δ𝑣̅
Δ𝑡→0 Δ𝑡
𝑑2 𝑟̅
𝑣̅̇ = 𝑑𝑡 2 = 𝑟̅̈ .𝑤
̅ = 𝑤𝑥 𝑖̅ + 𝑤𝑦 𝑗̅ + 𝑤𝑧 𝑘̅ = 𝑣̇𝑥 𝑖̅ + 𝑣̇𝑦 𝑗̅ + 𝑣̇𝑧 𝑘̅.Проекция
𝑤𝑥 = 𝑣̇ =
𝑑𝑣𝑥
𝑑𝑡
= 𝑥̈ =
вектора
d𝑣̅
=
d𝑡
=
ускорения
𝑑2 𝑥
…
𝑑𝑡 2
Рассмотрим движение частицы, совершаемое в плоскости. Скорость
направлена по касательной траектории, поэтому можно записать 𝑣̅ =
𝑣𝜏̅.Здесь единичный вектор 𝜏̅ задаёт направление касательной, 𝑤
̅ = 𝑣̇ 𝜏̅ +
𝑣𝜏̅̇.Ускорение𝑤
̅̅̅𝜏 = 𝑣̇ 𝜏̅, направленное по касательной к траектории,
определяемое скоростью изменение величины скорости, или модуля,
называется тангенциальным ускорением. 𝑤
̅=
𝑑𝑣
𝑑𝑡
𝑑𝜏
⃑⃑
𝜏⃑ + 𝑑𝑡 𝑣⃑ = ̅̅̅
𝑤𝜏 + ̅̅̅̅
𝑤𝑛 = 𝑣̇ 𝜏̅ +
𝑣2
𝑅
Δφ
Δ𝑡→0 Δt
̅
= dφ
=φ
̅̇ . При равномерном движении
dt
𝜑
вокруг неподвижной оси величина угловой скорости 𝜔 = 𝑡 . Естественным
образом обобщена на случай вращения с переменной 𝜔 понятие
𝜔
𝑁
количества оборотов, или частота вращения (𝜈 = 2𝜋, 𝜈 = 𝑡 ) и период (Τ =
2𝜋
𝜔
,
𝑡
Τ = 𝑁). При произвольном вращении угловая скорость может меняться как
по величине, так и по направлению. Для характеристики такого измерения
2
𝛥𝜔
вводится псевдовектор углового ускорения 𝛽̅ = 𝑙𝑖𝑚
= 𝑑𝜔̅=𝜔̅̇=𝑑 𝜑2 =𝜑̅̈. При
𝛥𝑡→0 𝛥𝑡
𝑑𝑡
𝑑𝑡
вращении тела вокруг неподвижной оси все его точки движутся по
окружности, скорости и ускорения различных точек различны, а угловые
𝑙
скорости и ускорения одинаковы. Угол, измеряемый в радианах 𝜑 = 𝑅, l –
𝑑𝑆
𝑑𝑡
=𝑅
𝑑𝜑
𝑑𝑡
= 𝑅𝜔)Точка
движется по окружности, поэтому у неё есть нормальное ускорение(𝑤𝑟 =
𝜔2 𝑅 =
𝑣2
𝑅
)и тангенциальное (𝑤𝜏 =
𝑑𝑣
𝑑𝑡
=
𝑑𝑅𝜔
𝑑𝑡
𝑑𝑝̅
и внешних) 𝑑𝑡 = 𝐹̅21 + 𝐹̅12 + ⨍внеш .(𝐹̅21 = −𝐹̅12 →
гелиоцентрическая система. Система связанная с землёй не инерциальна
т.к. Земля вращается вокруг Солнца(есть ускорение).Однако в условиях
задачи этим можно пренебречь и считать систему инерциальной. Пусть
относительно ИСО К поступательно со скоростью 𝑣0 движется СО К’.
Предполагаем, что при 𝑡0 = 0 начало систем ОО’ совпадает. Тогда 𝑟̅0 = 𝑣̅ 0 𝑡.
Радиус-векторы частицы в системе К и К’ связаны соотношением 𝑟̅ = 𝑣̅ 0 𝑡 +
𝑟̅ ′(по правилу сложения векторов). Т.к. движение К’ поступательное, то её
все точки движутся одинаково как О’. Поэтому скорости определим, взяв
производную.𝑣̅ = 𝑣̅ 0 + 𝑣̅ ′ - закон сложения скоростей Галилея.Если СО К
инерциальная, то и К’- ИСО.
4. Масса. Сила. Импульс. Второй закон Ньютона. Из 1-ого закона Ньютона
следует, что нужно объяснять не причины движения тела с некоторой
скоростью, а причины её изменения, т.е. возникновение ускорения.
Одинаковые воздействия на различные тела приводит к различным
ускорениям. Свойство тел различным образом реагировать на одинаковое
воздействие называется инертностью. Количественная мера инертности –
масса. Воздействие одних тел на другие в механике описывается с
помощью векторной величины силы. Силы складываются векторно вне
зависимости от их физической природы и дают результирующую силу. 2-ой
закон Ньютона: Cкорость изменения со временем физической величины,
называемой количеством движения, или импульсом тела, равна
̅̅̅̅
F
𝑑𝑣
𝑑𝑚𝑣
𝑑𝑝̅
действующей на тело силе.̅̅̅
w= p
или 𝐹̅ = 𝑚 =
= .Т.е. скорость
𝑑𝑡
𝑑𝑡
𝑑𝑡
изменения импульса тела равна результирующей сил, действующих на
тело. Векторная величина р̅ = 𝑚𝑣̅ называется импульсом материальной
точки (импульс – количество движения). Из 2-ого закона Ньютона следует,
что скорость изменения импульса механической системы равна сумме
𝑑𝑝̅
внешних сил, действующих на систему(внутренних и внешних) = 𝐹̅21 +
𝑑𝑡
𝑑𝑝̅
𝐹̅12 + ⨍внеш .(𝐹̅21 = −𝐹̅12 → 𝑑𝑡 = ⨍внеш )2-ой закон, как и 1-ый, справедлив только в
2
𝑑 х
ИСО. 𝐹̅х = 𝑚 𝑑𝑡 2 …
5. Третий закон Ньютона. Принцип относительности Галилея.
3-ий закон Ньютона: силы, с которыми 2 тела действуют друг на друга,
равны по величине, противоположны по направлению, лежат на одной
прямой, проходящей через тела и имеют одинаковую физическую
природу. 𝐹̅21 = −𝐹̅12 1-ый закон даёт критерий отыскания ИСО; 2-ой закон
даёт динамическое уравнение движения; 3-ий закон позволяет ввести в
рассмотрение все силы, действующие в системе. При переходе одной
ИСО в другую ИСО скорости преобразовываются по закону 𝑣̅ = 𝑣̅0 + 𝑣̅ ′, а
ускорение - 𝑤
̅=𝑤
̅′, т.е. ускорение тел не меняется, также как и силы,
следовательно, остаётся неизменным уравнение 2-ого закона. Закон
сохранения импульса. Векторная величина р̅ = 𝑚𝑣̅ называется импульсом
материальной точки (импульс – количество движения). Из 2-ого закона
Ньютона следует, что скорость изменения импульса механической
системы равна сумме внешних сил, действующих на систему(внутренних
𝑑𝑝̅
𝑑𝑡
= ⨍внеш )Система, на которую
не действуют внешние силы, называется замкнутой, или изолированной. Для
замкнутой системы
= 𝑅𝛽).
3. Первый закон Ньютона. Принцип относительности Галилея. Первый закон
Ньютона: Тело находится в состоянии покоя или прямолинейного
равномерного движения до тех пор пока воздействие со стороны других
тел не выведет его из этого состояния. Это свойство называется свойством
инерции, а закон – законом инерции. Очевидно, что закон инерции
выполняется не во всех системах отсчёта. СО, в которой выполняется 1ый
закон, называют инерциальной(ИСО).Современная формулировка 1ого
закона
Ньютона:
существуют
СО,
называемые
инерциальными,
относительно которых тела неподверженные воздействию других тел,
движутся
с
постоянной
скоростью.
Истинно
инерциальная-
m
𝑛̅
̅̅̅̅𝑛 – нормальное ускорение (характеризует быстроту изменения
𝑤
направления скорости), 𝑛̅ - единичный вектор, перпендикулярный 𝜏 и
направленный внутрь кривой, R – радиус кривизны линии.
2. Угловая скорость и угловое ускорение. Связь между угловыми и
линейными величинами.
Поворот абсолютно твёрдого тела на угол 𝜑 вокруг некоторой оси можно
задать с помощью направляющего отрезка 𝜑. 𝜑̅ – длина этого отрезка
совпадает сосью поворота, а направление параллельно оси вращения и
определяется правилом правого винта. Для 𝜑̅ не выполняется правило
сложения векторов.однако при бесконечно малых (элементарных)
поворотах 𝑑𝜑̅ правило сложения векторов выполняется. Как быстро
происходит вращение характеризует векторная (псевдовекторная)
величина угловая скорость𝜔
̅ = lim
длина дуги, на которую опирается угол, Δ𝑆 = 𝑅Δ𝜑.(𝑣 =
𝑑𝑝̅
𝑑𝑡
= 0, р̅ = со𝑛𝑠𝑡. Получаем закон сохранения импульса:
импульс замкнутой системы сохраняется (не меняется) со временем.1)
Импульс незамкнутой системы будет сохранятся, если внешние силы
компенсируют друг друга, и их результирующая = 0; 2) если
результирующая внешних сил ≠ 0, но = 0 её проекция на некоторое
направление (пр. ОХ), то проекция импульса на это направление будет
сохранятсяр̅х = со𝑛𝑠𝑡;закон изменения импульса: Изменение импульса
системы мат точек равно импульсу равнодействующей силы, вызывающей
2
это изменение. ⃑⃑⃑⃑
𝑝 − ⃑⃑⃑⃑
𝑝 = ∫ ⃑⃑⃑⃑
⨍ 𝑑𝑡
2
1
1
6. Центр масс.Пусть задана система материальных точек, массами
𝑚1 , 𝑚2… 𝑚𝑛 , радиус-векторы которых относительно некоторого начала О
𝑟1 , 𝑟2… 𝑟𝑛 . Точка С, радиус-вектор которой определяется выражением 𝑟̅𝑐 =
∑𝑛
𝑖=1 𝑚𝑖 𝑟̅𝑖
𝑚
, называется центром масс, или центром инерции системы. Её
положение относительно тел, не зависит от выбора О. Скорость центра
масс 𝑣̅𝑐 =
∑ 𝑚𝑖 𝑣 𝑖
𝑚
𝑝̅
= 𝑚. ИСО, связанную с центром масс, называют системой
центра масс. Центр масс движется так как если бы в нём была
сосредоточена вся масса и приложены все внешние силы.
7. Кинетическая энергия и работа.
𝜕𝐴 = (𝐹̅ , 𝑑𝑟̅ ) = ⋯ = |𝐹⃑ | ∙ |𝑑𝑟̅ |
Выражение
называется
работой,
совершённой силой 𝐹 при бесконечно малом перемещении 𝑑𝑟. 𝜕𝐴элементарная
работа(совершённая
на
бесконечно
малом
2
перемещении)𝐴𝑚 = ∫1 (𝐹̅ , 𝑑𝑟̅ ).Графический смысл: Работа-площадь фигуры
в координатах F от S. Отношение совершённой работы к промежутку
времени,
за
который
она
выполнялась
называется
средней
А
мощностью⟨Р⟩ = 𝑑𝑡.
lim
ΔА
Δ𝑡→0 Δ𝑡
= lim
Δ𝑡→0
(𝐹̅,Δ𝑟̅ )
Δ𝑡
При
Δ𝑡 → 0
получим
мгновенную
мощность
𝑃=
2
𝑑𝑣̅
𝑚𝑣
(𝐹̅ , 𝑑𝑟̅ ) = (𝑚 , 𝑣̅ 𝑑𝑡) = 𝑚(𝑣̅ , 𝑑𝑣̅ ) = 𝑚𝑣 ∙ 𝑑𝑣 = 𝑑( )–
𝑑𝑡
2
= (𝐹̅ , 𝑣̅ ).
2
кинетическая энергия.𝐴12 = ∫1 𝐹̅ 𝑑𝑟̅ = Ек2 − Ек1 – это закон изменения полной
механической энергии.
8. Поле сил. Консервативные силы. Потенциальная энергия частицы в поле.
Если работа, совершаемая над частицей не зависит от выбора траектории
движения, определяется только начальным и конечным положениями тел, то
такое поле называют потенциальным, а силы этого поля-консервативными.
(В потенциальном поле работа сил на любом замкнутом участке равна
нулю.) Работа будет зависеть от положения точки т.е будет функцией
2
радиус-вектора.𝐴12 = ∫1 𝐹̅ 𝑑𝑟̅ = 𝑈(𝑟̅ ). (𝑈(𝑟̅ )- функция потенциальной энергии
2
частицы в данной точке поля. 𝐴12 = ∫1 𝐹̅ 𝑑𝑟̅ = 𝑈2 − 𝑈1 .Потенциальная энергия
определяется не однозначно и зависит от выбора 0. 𝜕𝐴 = (𝐹̅ , 𝑑𝑟̅ ) = 𝐹𝑥 𝑑𝑥 +
𝐹𝑦 𝑑𝑦+𝐹𝑧 𝑑𝑧 = −𝑑𝑈 dU – полный дифференциал 𝑑𝑈 =
𝜕𝑈
𝜕𝑈
𝜕𝑈
𝐹̅ = −( 𝜕𝑥 𝑖̅ + 𝜕𝑦 𝑗̅ + 𝜕𝑧 𝑘̅) Силы
действующие
𝜕𝑈
𝜕𝑥
на
𝜕𝑈
𝜕𝑈
𝑑𝑥 + 𝜕𝑦 𝑑𝑦 + 𝜕𝑧 𝑑𝑧
частицу:
сторонние,
консервативные. 𝐸к +U=E. dE=𝜕Aстор .𝐸2 − 𝐸1 = Aстор .
9. Поле сил. Консервативные силы. Потенциальная энергия частицы в поле.
Если работа, совершаемая над частицей не зависит от выбора траектории
движения, определяется только начальным и конечным положениями тел, то
такое поле называют потенциальным, а силы этого поля-консервативными.
(В потенциальном поле работа сил на любом замкнутом участке равна
нулю.) Работа будет зависеть от положения точки т.е будет функцией
2
радиус-вектора.𝐴12 = ∫1 𝐹̅ 𝑑𝑟̅ = 𝑈(𝑟̅ ). (𝑈(𝑟̅ )- функция потенциальной энергии
2
частицы в данной точке поля. 𝐴12 = ∫1 𝐹̅ 𝑑𝑟̅ = 𝑈2 − 𝑈1 .Потенциальная энергия
определяется не однозначно и зависит от выбора 0. 𝜕𝐴 = (𝐹̅ , 𝑑𝑟̅ ) = 𝐹𝑥 𝑑𝑥 +
𝐹𝑦 𝑑𝑦+𝐹𝑧 𝑑𝑧 = −𝑑𝑈 dU – полный дифференциал 𝑑𝑈 =
𝜕𝑈
𝜕𝑈
𝜕𝑈
𝐹̅ = −( 𝜕𝑥 𝑖̅ + 𝜕𝑦 𝑗̅ + 𝜕𝑧 𝑘̅) Силы
действующие
на
консервативные. 𝐸к +U=E. dE=𝜕Aстор .𝐸2 − 𝐸1 = Aстор .
𝜕𝑈
𝜕𝑥
𝜕𝑈
𝜕𝑈
𝑑𝑥 + 𝜕𝑦 𝑑𝑦 + 𝜕𝑧 𝑑𝑧
частицу:
сторонние,
10. Полная мех энергия частицы в и системы частиц. Закон сохранения мех
энергии частицы и системы невзаимодействующих между собой
неконс
конс
неконс
частиц.( 𝑑𝐸к = ∂Аконс
+
внут + ∂Авнут + ∂Авнешн ; Авнут = −𝑑𝑈; → 𝑑(𝐸к + 𝑈) = ∂Авнут
∂Авнешн . Анек.с = Е2 − Е1 Мех Е частицы сохраняется если на частицу не
действуют сторонние силы или работа сторонних сил равна 0.Если на
частицу действуют неконсервативные силы, то приращение полной
механической энергии равно работе неконсервативных сил. Полная
механическая энергия замкнутой системы тел, между которыми действуют
только консервативные силы, остаётся постоянной. Если в замкнутой
системе действуют также неконсервативные силы, то полная механическая
энергия системы не сохраняется).
11. При взаимодействующих частицах: Е=𝐸к +𝑈внеш +𝑈вз .
внешн
относительно некоторой оси называют проекцию момента импульса на
эту ось. При движении частицы с постоянной скоростью момент импульса
̅ = [𝑟̅ , 𝐹̅ ] называется моментом силы
сохраняется. Векторная величина𝑀
относительно некоторой точки О. Моментом силы относительно некоторой
оси, проходящую через точку О, называют проекцию момента силы на эту
ось. Момент силы относительно некоторой оси характеризует способность
силы вызывать вращение вокруг этой оси. Моментом импульса
механической системы называется векторная сумма моментов импульса
частиц, образующих эту систему𝐿̅ = ∑𝑁𝑖=1 𝐿̅𝑖 .Суммарный момент всех
̅ = ⌈𝑟̅1 , ̅̅̅̅
внутренних сил относительно любой точки равен нулю(𝑀
𝐹12 ⌉ +
̅̅̅̅
̅̅̅̅
⌈𝑟̅2 , ̅̅̅̅
𝐹21 ⌉; (𝐹12 = −𝐹21 ) → ⌈𝑟̅,
̅2 , ̅̅̅̅
𝐹21 ⌉ = ⌈𝑟̅̅̅̅,
1 𝐹21 ⌉ − ⌈𝑟
21 𝐹21 ⌉ = 0).Таким образом, скорость
изменения момента импульса механической системы = сумме моментов
𝑑𝐿̅
̅𝑖внешн (𝑑𝐿̅ = ⌈𝑑𝑟̅ , 𝑝̅ ⌉ + ⌈𝑟̅ , 𝑑𝑝̅⌉ =
внешних сил, действующих на систему = ∑𝑁𝑖=1 𝑀
𝑑𝑡
𝑑𝑡
𝑑𝑡
̅𝑖внешн = 0, 𝐿 = 𝑐𝑜𝑛𝑠𝑡),
⌈𝑣̅ , 𝑟̅ ⌉ + ⌈𝑟̅ , 𝐹̅ ⌉ = ⌈𝑟̅ , 𝐹̅ ⌉, т. к⌈𝑣̅ , 𝑟̅ ⌉ = 0).Если система замкнута (𝑀
то выполняется
Штейнера: момент инерции 𝐼 относительно произвольной оси равен
сумме момента инерции 𝐼0 относительно оси, параллельной данной и
проходящей через центр инерции тела, и произведения массы тела 𝑚 на
вращающегося твёрдого тела. При вращении тела с угловой скоростью 𝜔
̅
все его элементарные массы движутся со скоростью 𝑣̅ 𝑖 = 𝜔
̅𝑅̅𝑖 ⇒они
обладают
кинетической
материальных
точек
остаётся
постоянным.
Закон
системы
сохранения
момента импульса выполняется также для незамкнутых систем, если
суммарный момент внешних сил = 0.Уравнение моментов: производная
момента импульса относительно некоторой оси по времени равна
моменту действующей на материальную точку силы относительно той же
𝑑𝐿̅
̅𝑖внешн .Mомент импульса замкнутой системы тел
оси.𝐿̅ = ∑𝑁𝑖=1 𝐿̅𝑖 , = ∑𝑁𝑖=1 𝑀
𝑑𝑡
относительно любой неподвижной точки не изменяется с течением
времени.Если момент внешних сил относительно неподвижной оси
вращения равен нулю, то момент импульса относительно этой оси не
изменяется.Может сохраняться не сам момент имрульса а его проекция
на некую ось, если момент внешних сил относительно оси вращения
равен нулю.
14 Вращение тела вокруг неподвижной оси. Рассмотрим произвольное
тело, ось вращения которого закреплена в неподвижных подшипниках.
Разобьём тело на элементарные массы 𝑚𝑖 , модуль момента импульса
которых𝐿𝑖 = [𝑟̅𝑖 , 𝑚𝑖 , 𝑣̅𝑖 ]. Тогда момент импульса точки относительно оси
2
OZ𝐿𝑖𝑧 = 𝑚𝑖 𝜔𝑧 𝑅̅𝑖 . Момент импульса всего тела относительно оси OZ 𝐿𝑧 =
2
𝜔𝑧 ∑ 𝑚𝑖 𝑅̅𝑖 = 𝜔𝑧 𝐼. Момент инерции твёрдого тела - сумма произведений
элементарных масс на квадрат их расстояния до произвольно выбранной
оси. Момент инерции зависит от выбора оси и распределения массы
𝑑𝐿̅
̅ внешн . Спроецируем это
тела. Воспользуемся уравнением моментов = М
𝑑𝑡
𝐸𝑘 =
2
,
𝐸 = ∑ 𝐸𝑘 =
𝜔2
2
𝐼–для
𝜔2
энергии = работе всех сил, действующих на тело𝑑𝐸𝑘 = 𝜕А = 𝑑 ( 2 𝐼) =
𝐼𝜔𝑧 ∙d𝜔𝑧 ;𝐼 ∙d𝜔𝑧 = 𝑀𝑧 ∙d𝑡 ;𝜔𝑧 =
𝑑𝜑
𝑑𝑡
𝜑
; 𝜕А = 𝑀𝑧 𝑑𝜑 → А = ∫0 𝑀𝑧 𝑑𝜑 ;
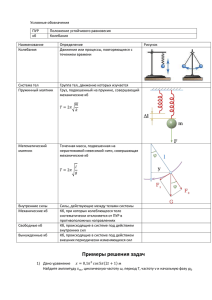
19. Малые колебания. Кинематическое уравнение гармонических
колебаний.
Колебания–процессы, характеризующиеся той или иной
степенью повторяемости по времени. Вынужденные— колебания,
протекающие в системе под влиянием внешнего периодического
воздействия. Свободные(или собственные) — это колебания в системе
,предоставленной самой себе, после того, как система выведена из
состояния равновесия (в реальных условиях свободные колебания всегда
затухающие).Автоколебания — вынужденные колебания при которых
моменты внешнего воздействия задаёт сама система. Параметрические
— колебания, возникающие при изменении какого-либо параметра
колебательной системы в результате внешнего воздействия.𝑈(𝑥) = 𝑈(0) +
𝑈(0)′ 𝑥
1!
+
𝑈(0)′′ 𝑥 2
2!
′
+ ⋯Так точка 0 точка устойчивого равновесия 𝑈(0) = 𝑚𝑖𝑛; 𝑈(0) =
0; 𝑈(0)′′ > 0, 𝑈(0)′′ = 𝑘 > 0; 𝑈(𝑥) = 𝑈(0) + 2 𝑘𝑥 2
∂U(x)
∂x
= Fx =-kx.Силы
пропорциональные
систему
в
положение
равноесия,
стремятся
называются
вернуть
квазиупругими.
𝑘
𝑘
колебания происходящие по закону синуса или косинуса под действием
𝑑𝑣(𝑡)
𝑑𝑡
𝑑𝑥(𝑡)
𝑑𝑡
2
𝜋
− 𝐴0 𝜔 s 𝑖𝑛( 𝜔0 𝑡 + 𝛼) = 𝐴0 𝜔 cos (𝜔0 𝑡 + 𝛼 + 2 ) 𝑤𝑥 =
2
− 𝐴0 𝜔0 cos( 𝜔0 𝑡 + 𝛼) = 𝐴0 𝜔0 cos(𝜔0 𝑡 + 𝛼 + 𝜋)При
2
2
2
t=0→ 𝑥 = А0 cos 𝛼;𝑣 2 =
𝑣0
𝑡𝑔𝛼 = − 𝑥 𝜔
0 0
А0 2 𝜔0 2 sin2 𝛼;{
.
2
√𝑥02 + 𝑣02 = 𝐴0
𝜔
Движение тела при гармоническом колебании происходит под действием
квазиупругой силы:𝐹𝑥 = −𝑘𝑥,которая является консервативной, а, значит,
выполняется закон сохранения энергии(неприрывний переход К в П и
наоборот)𝐸 = 𝐾 + 𝑈, 𝐾 =
𝑚𝐴02 𝜔02
K+U=
2
𝑚𝑣 2
2
=
𝑚𝐴0 2 𝜔02
𝑠𝑖𝑛2 (𝜔0 𝑡
2
̅=
+ 𝛼), 𝑈
𝑘𝑥 2
2
=
𝑘𝐴0 2
2
𝑐𝑜𝑠 2 (𝜔0 𝑡 + 𝛼) ⟹
.Среднее значение кинетической и потенциальной энергий по
времени: ⟨𝐾⟩ = ⟨𝑈⟩ =
𝑚𝐴02 𝜔02
4
угла
отклонения
𝜑(𝑡) = 𝜑0 cos(𝜔0 𝑡 +
𝑔
𝛼) , где циклическая частота 𝜔0 = √ 𝑙 . Период колебаний математического
маятника
2𝜋
𝑙
Τ = 𝜔 = 2𝜋√𝑔.
Твёрдое
0
тело,
способное
вращаться
вокруг
некоторой оси ОО’, непроходящее через центр масс тела (С) и
находящееся в однородном поле силы тяжести, называют физическим
маятником. При колебании тело совершает вращательное движение,
̅𝑧 внешн . При
следовательно, его движение подчиняется уравнению 𝐼𝛽𝑧 = 𝑀
малых колебаниях 𝑀𝑧 = −𝑙𝑚𝑔 sin 𝜑 = −𝑙𝑚𝑔𝜑. 𝐼𝜑̈ = 𝑙𝑚𝑔𝜑. 𝑙 – расстояние от
центра масс до оси вращения OO’. 𝐼 – момент инерции тела относительно
оси
вращения
OO’.
угол отклонения 𝜑 меняется по гармоническому
𝜑̈ +
𝑙𝑚𝑔
закону.
𝜔0 = √𝐼
OO’
𝑙𝑚𝑔
𝐼
𝜑=0⟹
,Τ = 2𝜋√
𝑙𝑚𝑔
𝐼
.
Приведённа
длинна
физического
маятника-длинна
такого
математического мятника Т которых совпадает.
23. Затухающие колебания.
В реальных физических системах всегда действуют силы сопротивления, в
результате действия которых амплитуда колебаний с течением времени
убывает. рассмотрим движение тела в вязкой среде, когда силы
⃑⃑⃑⃑⃑⃑⃑⃑⃑
⃑⃑⃑⃑⃑⃑⃑⃑⃑
сопротивления противоположны скорости движения тела:mw=𝐹
кваз + 𝐹сопр →
𝑚𝑥̈ = −𝑟𝑥̇ − 𝑘𝑥, 𝐹𝑐опр = −𝑟𝑥̇ , 𝑟 –коэффициент сопротивления. 𝑥̈ + 2𝛽𝑥̇ + 𝜔02 𝑥 =
𝑟
𝑘
0, 𝛽 = 2𝑚 , 𝜔02 = 𝑚. 𝑥(𝑡) = 𝐴0 𝑒 −𝛽𝑡 cos(𝜔𝑡 + 𝜑0 ) –кинематический закон затухающих
колебаний. Можно сказать, что наблюдаются гармонические колебания с
частотой
𝜔 = √𝜔02 − 𝛽 2 ,
амплитуда
же
колебаний
убывает
по
экспоненциальному законуА = 𝐴0 𝑒 −𝛽𝑡 . Скорость затухания определяется
𝑟
величиной коэффициента затухания𝛽 = 2𝑚. Затухание характеризуется
также декрементом затухания, который показывает во сколько раз
2𝜋
уменьшилась амплитуда колебаний за время, равное периоду Τ = 𝜔 :
0
𝐴(𝑡)
= 𝑒 𝛽𝑇 . Логарифм
этого
выражения называют
логарифмическим
1
.
21-22. Математический маятник. Физический маятник. Небольшое тело
массой 𝑚, подвешенное на лёгкой нерастяжимой нити длины 𝑙,
находящееся в однородном поле силы тяжести, называют математическим
маятником.При отклонении от положения равновесия тело будет двигаться
по дуге окружности, следовательно, его движение описывается основным
̅𝑧 внешн , 𝑀
̅ = [𝑟̅ , 𝑚𝑔̅ ] + [𝑟̅ , 𝑇̅] = [𝑟̅ , 𝑚𝑔̅ ] + 0 ⟹ 𝑀𝑧 =
уравнением динамики 𝐼𝛽𝑧 = 𝑀
𝜏
1
уменьшается в е раз(𝑒 𝛽𝜏 = е → 𝛽 = 𝜏 .).за время затухания→ 𝑁 = 𝑇 = 𝜆
В
затухающих
системах
используется
𝐸(𝑡)
добротность:
уравнение:𝑥(𝑡) = 𝐴0 cos(𝜔0 𝑡 + 𝛼)Гармонические-
квазиупругой силы. 𝑣𝑥 =
изменение
декрементом затухания: 𝜆 = 𝛽𝑇.Время релаксации-время за которое А
смещению
𝑚𝑥̈ = −𝑘𝑥 → 𝑥̈ + 𝑚 𝑥 = 0, 𝜔0 =
√𝑚 ⇒.Динамическое
𝑙𝑚𝑔 sin 𝜑. Рассмотрим малые отклонения от положения равновесия, тогда
𝑔
sin 𝜑 = 𝜑 ⟹ 𝑀𝑧 = 𝑙𝑚𝑔𝜑. 𝐼 = 𝑚𝑙 2 , 𝛽𝑧 = 𝜑̈ .Подставим всё в: 𝜑̈ + 𝑙 𝜑 = 0 ⟹
𝐴(𝑡+𝑇)
1
Динамическое ур − ние:
замкнутой
энергией
𝑚𝑖 𝑅𝑖2𝜔 2
тела,вращающегося вокруг неподвижной оси. Приращение кинетической
момента
импульса
=
элементарный объём, 𝜌 – плотность вещества. 𝐼 = ∫𝑉 𝜌(х, у, 𝑧)𝑅2 𝑑𝑉. Теорема
−
момент
𝑑𝑡
̅𝑧
̅𝑧
𝑀
⇒ 𝐼𝛽𝑧 = 𝑀
- основное уравнение динамики вращательного
движения, 𝛽 – угловое ускорение тела.𝐼является аналогом 𝑚и характеризует
инертность тела по отношению к вращению. Если суммарный момент
внешних сил = 0, а в пределах тела происходит перемещение масс, то
проекция момента импульса сохраняется 𝐿𝑧1 = 𝐿𝑧2 . Момент инерции.
Теорема Штейнера. Момент инерции определяется как 𝐼 = ∑ 𝑚𝑖 𝑅𝑖2 , если
распределение массы равномерно, то 𝑚𝑖 заменяется на 𝜌𝑑𝑉, 𝑑𝑉 –
13. Закон сохранения момента импульса частицы и системы частиц.
Импульс момента силы. Уравнение моментов закон сохранения
импульса:
𝑑𝜔𝑧
внешн
квадрат расстояния а между осями: 𝐼 = 𝐼0 + 𝑚𝑎2 . Кинетическая энергия
12. Момент импульса. Момент силы. Моментом импульса частицы
относительно некоторой точки О называется векторная (псевдовекторная)
величина 𝐿 = [𝑟̅ , 𝑝] = 𝑚[𝑟̅ , 𝑣].Свойства: 1) Зависит от выбора точки О; 2)
Модуль L= r p sin𝛼=𝑙𝑝 = r m v sin𝛼; 3) L– плечо,𝑙 ̅ ⊥ 𝑣,
̅ 𝑙 ̅ ⊥ 𝑝̅ . Моментом импульса
𝑑𝑡
уравнение на ось OZ и подставим в полученную формулу для 𝐿𝑧 : 𝐼
𝑄 = 2𝜋 𝐸(𝑡)−𝐸(𝑡+𝑇) ;Энергия
𝐴2 (𝑡)
также
такая
колебаний
величина
как
пропорциональна
𝜋
квадрату амплитуды→ 𝑄 = 2𝜋 𝐴2 (𝑡)−𝐴2 (𝑡+𝑇);А = 𝐴0 𝑒 −𝛽𝑡 → 𝑄 = 𝛽𝑇;
27. Векторная диаграмма. Вынужденные колебания. При сложении
нескольких колебаний одинакового направления удобно использовать
метод векторных диаграмм. В этом методе колебанию 𝑥(𝑡) = 𝑎0 cos(𝜔0 𝑡 +
𝜑0 ) сопоставляется вектор а̅, модуль которого равен амплитуде колебаний,
а направление задаётся углом 𝜑 = 𝜔0 𝑡 + 𝜑0 , отсчитанным от некоторого
направления ОХ: 𝑥 = 𝑎 cos 𝜑. С течением времени а̅ вращается вокруг точки
О с угловой скоростью 𝜔.
Пусть заданы 2 колебания одинаковой частоты : 𝑥1 = 𝑎1 cos(𝜔 𝑡 + 𝜑01 ), 𝑥2 =
𝑎2 cos(𝜔 𝑡 + 𝜑02 ). Результирующее колебание х = 𝑥1 + 𝑥2 будет совпадать с
проекцией
вектора
а̅ = а̅1 + а̅2
на
ОХ.∑ проекций векторов =
проекции ∑ векторов.Амплитуда результирующих колебаний 𝑎2 = 𝑎12 + 𝑎22 −
2𝑎1 𝑎2 cos(𝜑2 − 𝜑1 ).
Начальная фаза результирующих колебаний определяется уравнением
𝑡𝑔𝜑 =
𝑎1𝑦 +𝑎2𝑦
𝑎1𝑥 +𝑎2𝑥
𝑎 sin 𝜑 +𝑎 sin 𝜑
= 𝑎 1 cos 𝜑1+𝑎2 cos 𝜑2 . Вынужденными называются такие колебания,
1
1
2
2
которые возникают в колебательной системе под действием внешней
периодически
изменяющейся
силы
(вынуждающая
сила).
Пусть
вынуждающая сила меняется по гармоническому закону𝐹𝑥 = 𝐹0 cos 𝜔𝑡. С
учётом сил сопротивления и упругости получим динамическое уравнение
движения
системы:
𝑚𝑥 ′′ = −𝑘𝑥 − 𝑟𝑣 + 𝐹0 cos 𝑤 𝑡 ; 𝑥 ′′ + 2𝛽𝑥 ′ + 𝑤02 𝑥 =
𝐹
𝑟
𝑘
𝑓0 cos 𝑤 𝑡 , 𝑓0 = 𝑚 , 𝛽 = 2𝑚 , 𝜔0 = √𝑚.Предположим, что система совершает
гармонические колебания с частотой 𝜔, отставая по фазе от
вынуждающей силы на 𝜑. ⟹ 𝑥 = А cos(𝜔 𝑡 − 𝜑 ). Находим 1-ую и 2-ую
производные и подставляем в динамическое уравнение движения системы:
𝜋
2
левой
2
𝐴𝜔 cos(𝜔𝑡 + 𝜑 + 𝜋) + 2𝛽𝐴𝜔 cos (𝜔𝑡 − 𝜑 + 2 ) + 𝜔0 𝐴 cos(𝜔𝑡 − 𝜑) = 𝑓0 cos 𝜔𝑡.В
части стоит сумма 3-х колебаний одинаковой частоты, сдвинутой по фазе и
с различными амплитудами. При 𝑡 = 0 фаза результирующих колебаний
2𝛽𝜔
должна равняться 0. Начальная фаза 𝜑 определена условием:𝑡𝑔𝜑 = 𝜔2−𝜔2 .
0
В отличие от гармонических и затухающих колебаний частота вынужденных
колебаний не определяется свойствами системы, а только частотой
вынуждающей силы. При некоторой определённой для данной системы
частоте 𝜔, амплитуда достигает максимального значения. Колебательная
система оказывается особенно отзывчивой на действие вынуждающей
силы при этой частоте. Это явление называется резонансом, а частота –
резонансной частотой. 𝑤р = √𝑤02 − 2𝛽 2 , 𝑎р = 2𝛽
𝑓 0
√𝑤0 2−𝛽 2
.
24-26. Биение. Сложение взаимно перпендикулярных колебаний.
Биение – колебание, возникающее в рез-те сложения гармонических
колебаний одного и того же направления со слабо отличающимися
частотами. Рассмотрим случай сложения 2-ух колебаний одинакового
направления, частота которых незначительно отличается друг от друга:𝜔, 𝜔 +
Δ𝜔. При этом возникают колебания, амплитуда которых периодически
меняется от некоторого максимального значения до минимального.
Рассмотрим простой случай, когда амплитуды и начальные фазы обоих
колебаний равны. Сложим оба уравнения волны по принципу
суперпозиции.
Данное
колебание
можно
рассматривать
как
2𝜋
гармоническое с частотой 𝜔 и периодом Τ = 𝜔 . Однако амплитуда этого
колебания медленно меняется в пределах от 0 до 2а с частотой Δ𝜔 и
2𝜋
периодом Τ = Δ𝜔 . В таком случае говорят, что наблюдаются биения.
Пусть 2 гармонических колебания совершаются системой во взаимно
перпендикулярных направлениях по закону х = а cos 𝜔 𝑡, у = 𝑏 cos(𝜔 𝑡 + 𝛼). В
результате сложения этих колебаний частица будет двигаться по некоторой
траектории в плоскости ХОУ. Производим вычисления и получаем
уравнение
траектории
движения
частицы:
𝑥2
𝑦2
𝑥𝑦
+ 𝑏2 − 2 𝑎𝑏 cos 𝛼 = sin2 𝛼
𝑎2
–
уравнение эллипса. При 𝛼 = 0 или 𝛼 = 𝜋 эллипс вырождается в отрезок,
проходящий через начало координат
𝑥2
𝑥
𝑎
𝑦
= ± 𝑏 . При получаем уравнение
𝑦2
эллипса :𝑎2 + 𝑏2 = 1. В колебательной системе колебания можно возбудить и
поддерживать не только благодаря внешнему воздействию, но и в
результате изменения периодичным образом параметров в системе. При
этом наблюдается явление параметрического резонанса. При колебании
математический маятник будет уменьшать его длину в положении
равновесия, когда сила натяжения максимальная, и увеличивать длину при
прохождении амплитудных точек, когда сила натяжения минимальная.
Результирующая работа будет положительной. Эта работа идёт на
приращение механической энергии маятника, его амплитуда колебаний
увеличивается.
Фигуры
Лиссажу
возникают
в
рез-те
сложений
взаимноперпендикулярных колебаний. Уравнения биений имеют вид:
𝑥 = |2𝐴𝑐𝑜𝑠
𝑢1 −𝑢2
2
𝑡| ∙ 𝑐𝑜𝑠
𝑢1 +𝑢2
2
𝑡
Биения
гармонические колебания с частотой
можно
рассматривать
как
𝑢1 +𝑢2
2
28,29,33. Распространение волн в упругой среде. Уравнение плоской и
сферической волны.
Если в каком-либо месте упругой среды (тв., жидк., газообр.) возникают
колебания её частиц, то из-за взаимодействия между частицами эти
колебания будут распространяться в среде от частицы к частице с
некоторой скоростью v. Процесс распространения колебаний в
пространстве называют волной. При этом частицы среды не совершают
поступательного движения вместе с волной, а колеблются вблизи своего
положения равновесия. В зависимости от направления колебаний частиц
по отношению к направлению распространения волны различают
продольные (частицы колеблются вдоль направления распространения
волны) и поперечные(частицы колеблются перпендикулярно направлению
распространения волны) волны. Продольные волны возникают в средах, где
существуют упругие деформации сжатия или растяжения. Поперечные
волны
возникают
при
наличии
упругой
деформации
сдвига.
Геометрическое место точек, до которых доходят колебания к некоторому
моменту времени, называют фронтом волны. Он перемещается в
пространстве со временем. Геометрическое место точек, колеблющихся в
одинаковой фазе, называют волновой поверхностью. 𝑣 = 𝜆𝜈.Длина волны –
расстояние между 2-мя ближайшими точками, совершающими колебания
с разностью фаз 2𝜋. В зависимости от формы волновой поверхности
различают плоские, сферические и цилиндрические волны. Уравнением
волны называется функция координат и времени, определяющая
смещение точек среды из положения равновесия в любой момент
времени во всём пространстве.
𝜔
Уравнение плоской волны𝜀 = 𝑎 cos(𝜔𝑡 − 𝑘𝑟), 𝑘 = 𝑣 , 𝑘 – волновое число или 𝑆 =
𝑎 cos(𝜔𝑡 − 𝑘𝑥 𝑥 − 𝑘𝑦 𝑦 − 𝑘𝑧 𝑧 + 𝛼), 𝑘 =
𝜔
𝑣
Уравнение сферической волны𝜀 =
𝑎0
𝑟
𝑟
cos (𝜔(𝑡 − 𝑣)) .
−𝑘𝑥 2 𝑎 cos(𝜔𝑡 − 𝑘𝑟), 𝜀̈𝑦𝑦 = −𝑘𝑦 2 𝑎 cos(𝜔𝑡 − 𝑘𝑟), 𝜀̈𝑧𝑧 =. . .Можно записать :𝜀̈𝑥𝑥 + 𝜀̈𝑦𝑦 +
1
𝜀̈𝑧𝑧 = 𝜔2 𝜀̈𝑡𝑡 = 𝑣 𝜀̈𝑡𝑡
–
волновое
уравнение.
Волновому
уравнению
будет
удовлетворять любая волна произвольной частоты 𝜔, распространяющаяся
со скоростью 𝑣. 𝑣 определяется физическими свойствами среды. В случае
плоской волны, распространяющейся в направлении по х, волновое
𝑘2
1
уравнение записывается в виде: 𝜀̈𝑥𝑥 = 𝜔2 𝜀̈𝑡𝑡 = 𝑣 𝜀̈𝑡𝑡 .
31-32. Энергия упругой волны. Плотность потока энергии.
Пусть плоская продольная волна распространяется в направлении ОХ в
некоторой упругой среде. Её уравнение: 𝜀 = 𝑎 cos(𝜔𝑡 − 𝑘𝑟 + 𝛼). Частицы
среды, отклоняясь от положения равновесия, движутся с некоторыми
скоростями. Следовательно, они обладают кинетической и потенциальной
энергиями. Выделим в среде цилиндрический объем ∆V с площадью
основания ∆S и высотой ∆x. Его величина такова, что можем считать
𝑑 𝜀
скорости частиц𝑑𝑡
𝐸 = 𝜌𝑣 2 =
𝑘Δx
Δ𝑆
и относительное смещение
𝑑𝜀
𝑑𝑥
𝐸
одинаковыми. 𝑣 = √𝜌 ⟹
− модуль Юнга ⟹ Энергия, заключённая в этом объёме 𝑊 =
𝑊кмнетическая + 𝑊потенциальная =
𝜌Δ𝑉
2
𝑑 𝜀
2
(𝑑𝑡 ) +
𝑊
𝜌
𝐸Δ𝑉
𝑑 𝜀
2
2
𝑑𝜀 2
(𝑑𝑥) .
𝐸
Таким
образом,
плотность
𝑤
плоской волны, преобразуем и воспользуемся тем, что 𝑘 = 𝑣 :𝑊 = ⋯ =
2
sin2 (𝜔𝑡 − 𝑘𝑥 + 𝛼).Затем
энергии: ⟨𝑊⟩ =
𝜌𝑎 2 𝜔 2
2
найдём
среднюю
по
периоду
плотность
. Из выражения для плотности энергии видно, что её
величина меняется со временем от 0 до некоторого максимального
значения, а значит, энергия от источников колебания переносится волной из
одного места пространства в другое со скоростью 𝑣. Волна осуществляет
процесс переноса энергии, но не вещества. Перенос энергии
осуществляется посредством сил упругого взаимодействия между
частицами среды. Количество энергии, переносимое через некоторую
поверхность за единицу времени, называется потоком энергии через эту
𝑊
поверхность: Ф = Δ𝑡 =
𝑑𝑊
𝑑𝑡
ΔS
𝑑𝑊
= 𝑑𝑡𝑑S = 𝑊𝑣 – последнее – вектор Умова.
Среднее⟨𝑗̅⟩ = ⟨𝑊⟩𝑣̅ =
𝜌𝑎 2𝜔 2
2
𝑣̅ (интенсивность волны) Модуль этого выражения
называется интенсивностью волны.
34. Стоячие волны. Если в среде распространяется несколько волн, то
частицы среды будут совершать колебания, равные векторной сумме
колебаний, возникающих от каждой из волн, взятые по отдельности. Это
положение называется принципом суперпозиции, и оно следует из опытных
данных. Когда колебания, обусловленные отдельными волнами, в каждой из
точек среды обладают постоянной разностью фаз, то их называют
когерентными. При наложении когерентных волн наблюдается их
интерференция, т.е. усиление в одних точках пространства и ослабление в
других. Важным случаем интерференции является наложение 2-ух
встречных волн (одна из них может быть отражённой волной). В этом случае
возникают стоячие волны. Запишем уравнения 2-ух плоских волн,
распространяющихся вдоль ОХ в противоположном направлении, и
сложим их: 𝑆1 (𝑥, 𝑡) = 𝑎 cos(𝜔𝑡 − 𝑘𝑥) 𝑆2 (𝑥, 𝑡) = 𝑎 cos(𝜔𝑡 + 𝑘𝑥)В рез-те сложения:
𝑘𝑥+𝛼2 −𝛼1
2
cos(𝜔𝑡 +
𝛼1 +𝛼2
2
) ⟹ 𝜀 = 2𝑎 cos
2𝜋
𝜆
х cos 𝜔𝑡 , если 𝑘 =
2𝜋
𝜆
, 𝛼2 − 𝛼1 =
0, 𝛼1 + 𝛼2 = 0. Таким образом, в каждой точке пространства совершаются
гармонические колебания частоты 𝜔. Амплитуда этих колебаний меняется
от 0 до 2𝑎 по законуА = 2𝑎 cos
2𝜋
𝜆
х. Точки, в которых амплитуда достигает
максимальной величины, называются пучностями стоячей волны, их
х
координаты: 2𝜋 𝜆 = ±𝑛𝜋. Точки, где амплитуда обращается в 0, называются
х
1
узлами стоячей волны, их координаты: 2𝜋 𝜆 = ±(𝑛 + 2)𝜋. Расстояние между
соседними пучностями (узлами) равно половине длины волны.
35.
Внутренняя энергия термодинамической системы. Первое
начало термодинамики.
Внутренняя энергия тела складывается из кинетической энергии
поступательного
и
вращательного
движений,
кинетической
и
потенциальной энергий колебательного движения атомов, молекулы,
внутренней
молекулярной
энергии,
потенциальной
энергии
взаимодействия молекул тела. Во внутреннюю энергию не входит
кинетическая энергия тела как целого и потенциальная энергия тела во
внешнем силовом поле.если система состоит из 2-ух тел, то обычно
энергия взаимодействия между телами значит меньше внутренней энергии
тел, поэтому энергией взаимодействия можно пренебречь, значит,
внутренняя энергия системы 𝑈 = 𝑈1 + 𝑈2 . Внутренняя энергия зависит только
от состояния тела, т.е. её значение определяется параметрами состояния.
Поэтому можно говорить о приращении внутренней энергии ∆𝑈 = 𝑈2 − 𝑈1 в
ходе термодинамического процесса. Для элементарных процессов ∆𝑈
заменяется на 𝑑𝑈. Изменение внутренней энергии может происходить в
основном за счёт 2-ух процессов:
𝑑𝜀 2
энергии упругой волны𝑊 = Δ𝑉 = 2 (𝑑𝑡 ) + 2 (𝑑𝑥) . Подставим в него уравнение
𝜌𝑎 2𝜔 2
ΔФ
По направлению он совпадает с направлением распространения волны.
𝜀 = 2𝑎 cos
31. Волновое уравнение.
Уравнение любой волны есть решение некоторого дифференциального
уравнения, называемого волновым. Исходя из физических свойств среды и
основных законов механики мы получаем волновое уравнение из явного
выражения для уравнения плоской волны.
𝜀 = 𝑎 cos(𝜔𝑡 − 𝑘𝑟) = а cos(𝜔𝑡 − 𝑘𝑥 , 𝑥 − 𝑘𝑦 , 𝑦 − 𝑘𝑧 , 𝑧 + 𝛼).𝜀̈𝑡𝑡 = −𝜔2 𝑎 cos(𝜔𝑡 − 𝑘𝑟) , 𝜀̈𝑥𝑥 =
𝑘2
площадь этой площадки: |𝑗̅| = 𝑗 =
. Для более детальной характеристики процесса
переноса энергии используется вектор плотности потока энергии 𝑗̅. По
величине он равен потоку энергии, переносимой через площадку,
перпендикулярную направлению распространения волны, делённому на
Внешние тела, действующие на систему, совершают некую работу А′ над
системой. соответственно термодинамическая система в силу 3-его
закона Ньютона совершает работу А = А′.Изменение внутренней энергии
может происходить за счёт передачи телу теплоты. Когда отдельные
молекулы более нагретого тела передают часть своей энергии отдельным
молекулам менее нагретого тела. Совокупность микропроцессов,
приводящих к передаче энергии от одного тела к другому, называется
теплоотдачей.
Она
может
происходить
за
счёт
конвекции
теплопроводности излучения (перенос энергии за счёт движения частиц
вещества). Количество энергии, переданное телу за счёт микропроцессов,
называется количеством теплотыQ. Исходя из всеобщего ЗСЭ можем
записать 1-ое начало термодинамики: Q = ∆𝑈 + А. Количество теплоты,
получаемое системой, идёт на приращение внутренней энергии системы
и совершение его работы над внешними телами для элементарных
процессов 𝑑Q = 𝑑𝑈 + 𝑑А, 𝑄 ≠ 𝑄2 − 𝑄1 .
36.
Внутренняя энергия и
теплоёмкость
идеального
газа.
Адиабатический процесс.
Количество теплоты, необходимое для нагревания тела на 1 кельвин
единицы массы тела (вещества), называется удельной теплоёмкостью:
Стела =
𝑑′𝑄
𝑑𝑇
𝑑′𝑄
. 𝐶 = 𝑐𝑀, 𝑐 = 𝑑𝑇𝑑𝑚 .Количество теплоты, необходимое для нагревания
тела на 1 кельвин 1 моля вещества, называется молярной теплоёмкостью.
Теплоёмкость зависит от условий, при которых происходит нагревание
тела. Выделяют теплоёмкость при постоянном объёме 𝐶𝑣 и при постоянном
давлении. Экспериментально установлено, что 𝐶𝑣 не зависит от
температуры, следовательно, внутренняя энергия 1 моля идеального газа
𝑈𝑀 = 𝐶𝑣 𝑇. Для 𝜇 молей в силу аддитивной внутренней энергии 𝜇М = С𝑣𝑇.
Молярная теплоёмкость при постоянном давлении р𝐶𝑝 =
[𝑉 =
𝑅𝑇
𝑝
Мойера.
] = 𝐶𝑣 + 𝑅–уравнение
Отношение
𝛾=
𝑑𝑈𝑀
𝑑𝑇
𝑑𝑉
+ 𝑝 (𝑑𝑇 ) =
𝑝
𝐶𝑝
является
𝐶𝑣
характеристикой газа, оно определяется числом степеней молекулы газа и
𝑅
характером.
𝐶𝑣 = 𝛾−1.
Адиабатный
процесс:
0 = 𝑑𝑈 + 𝛿𝐴, 𝛿𝑆 = 0.
Термодинамический процесс, при котором не происходит теплообмена с
внешней средой, называется адиабатическим.
37.
Уравнение адиабаты идеального газа. Работа, совершаемая
газом при различных процессах.
Термодинамический процесс, при котором не происходит теплообмена с
внешней средой, называется адиабатическим. 𝑑′𝑄 и в соответствии с 1-ым
началом термодинамики можно записать: 0 = 𝑑 ′ А + 𝑑𝑈 = 𝜈𝐶𝑣 𝑑𝑇 +
Отсюда
получаем
𝑑Т
Т
𝑅𝑑𝑉
+𝐶
𝑣𝑉
𝜈𝑅𝑇
𝑉
𝑑𝑉.
𝑅
= 0 ⟹ ln Т + ln 𝑉 𝐶𝑣 = 𝑐𝑜𝑛𝑠𝑡 ⟹ ln Т𝑉 𝛾−1 = 𝑐𝑜𝑛𝑠𝑡.
Окончательно получаем уравнение адиабатыТ𝑉
= 𝑐𝑜𝑛𝑠𝑡. Уравнение
адиабаты с переменными 𝑝, 𝑉: 𝑝𝑉 𝛾 = 𝑐𝑜𝑛𝑠𝑡 – называется уравнением
Пуассона.
Вычислим работу идеального газа для некоторых процессов:
𝑉
1)
изобарический процесс𝑝 = 𝑐𝑜𝑛𝑠𝑡: 𝐴12 = ∫𝑉 2 𝑝𝑑𝑉 = 𝑝(𝑉2 − 𝑉1 );
𝛾−1
1
2)
0;
изохорический процесс 𝑉 = 𝑐𝑜𝑛𝑠𝑡:𝑑𝑉 = 0 ⟹ 𝑑 А = 𝑝𝑑𝑉 = 0 ⟹ 𝐴12 =
3)
изотермический
′
𝑉 𝜈𝑅𝑇
1
1
𝑉
𝑉2 𝑝1 𝑉1𝛾
𝑉1 𝑉 𝛾
Пуассона:𝑝𝑉 𝛾 = 𝑐𝑜𝑛𝑠𝑡 ⟹ 𝑝1 𝑉1 𝛾 = 𝑝2 𝑉2 𝛾 , 𝐴12 = ∫𝑉 2 𝑝𝑑𝑉 = ∫
𝑉
𝑑𝑉 =
1
𝑉 𝑑𝑉
𝑑𝑉 = 𝑝1 𝑉1 𝛾 ∫𝑉 2 𝑉 𝛾 =
1
𝑝
1
(𝑉1 𝛾 𝑉2 𝛾−1 − 𝑉1 ).
⋯ = 𝛾−1
42. Барометрическая формула.
Барометрическая формула даёт зависимость атмосферного давления от
высоты, отсчитанной от поверхности Земли. Предполагается, что
температура атмосферы с высотой не меняется. Для вывода формулы
выделим вертикальный цилиндр: поперечное сечение S. В нём выделяется
небольшой цилиндрический объём высотой dh. Он находится в
равновесии: на него действуют сила тяжести mg, вертикально
направленная вверх сила давления газа F1 и вертикально направленная
вниз сила давления F2. Их сумма = 0. В проекции: -mg+F1-.F2=0 ⟹ −𝜌𝑆𝑑ℎ𝑔 +
𝑆𝑝 − 𝑆(𝑝 + 𝑑𝑝) = 0 ⟹ 𝑑𝑝 = −𝜚𝑔𝑑ℎ.Из уравнения Клапейрона-Менделеева 𝑝𝑉 =
𝑀
⟹
𝑑𝑝
𝑝
𝑀𝑔
= − 𝑅𝑇 𝑑ℎ. Интегрируем в пределах от 0 до ℎ и получаем: 𝑝 =
𝑀𝑔ℎ
𝑅𝑇
𝑝0 𝑒
– барометрическая формула, используемая для определения
высоты.
Изменением
в
температуре
можно
пренебречь. 𝑚𝑔ℎ −
потенциальная энергия частицы на высоте h
38.
Давление газа на стенку.
−
Давление,
оказываемое
газом
на
стенки
𝐹
сосуда: 𝑝 = 𝑆 .Возьмем
произвольный объем 𝑆𝑣𝑥 𝑑𝑡. К каждой из стенок за время dt подлетит 1/6
всех молекул. Каждая молекула обладает импульсом: 𝑚0 𝑣𝑥 . При
абсолютно пругком ударе стенка получит импульс: 2𝑚0 𝑣𝑥 . Общий импульс
который
1
1
получит
1
стенка
1
S: 6 𝑛𝑆𝑣𝑥 𝑑𝑡(2𝑚0 𝑣𝑥 )
𝑛2𝑚0 𝑣𝑥 𝑣𝑥 𝑆𝑑𝑡 = 3 𝑚0 𝑛𝑣𝑥2 𝑆𝑑𝑡. Отсюда
6
𝐹
𝑆
1
следовательно
𝐹𝑑𝑡 =
= 3 𝑚0 𝑛𝑣𝑥2 = 𝑝. Молекулы имеют разные
2
Таким образом 𝑝 = 3 𝑚0 𝑛⟨𝑣 2 ⟩ = 3 𝑛
𝑚0 ⟨𝑣 2⟩
2
- основное уравнение молекулярно –
кинетической теории газов. Давление газов определяется средней
кинетической энергией поступательного движения молекул.
38-39. Распределение по скорости, по компонентам скоростей..
Распределение Максвелла дает распределение частиц по скоростям и
компонентам скоростей: вероятность того, что компонента скорости 𝑣𝑥
некоторой молекулы имеет значение в пределах от 𝑣𝑥 до 𝑣𝑥 + 𝑑𝑣𝑥 может
быть представлена в виде : 𝑑𝑃𝑥 =
компонент
скорости 𝑑𝑃𝑦 =
𝑑𝑛𝑥
𝑛𝑥
𝑑𝑛𝑦
𝑛𝑦
= 𝜑(𝑣𝑥 )𝑑𝑣𝑥 Соответственно для других
= 𝜑(𝑣𝑦 )𝑑𝑣𝑦 𝑑𝑃𝑧 =
𝑑𝑛𝑧
𝑛𝑧
= 𝜑(𝑣𝑧 )𝑑𝑣𝑧 Вероятнсоть
одновременного наблюдения независимых событий равна произведению
вероятностей этих событий : 𝑑𝑃𝑥,𝑦,𝑧 = 𝜑(𝑣𝑥 )𝜑(𝑣𝑦 )𝜑(𝑣𝑧 )𝑑𝑣𝑥 𝑑𝑣𝑦 𝑑𝑣𝑧 Для функций
1
𝑚
𝑚𝑣 2
распределения были получены выражения: 𝜑𝑥 = (2𝜋𝑘𝑇 )2 exp(− 2𝑘𝑇𝑥 ) Для 𝜑𝑦 и 𝜑𝑧
меняются только 𝑣𝑦 и 𝑣𝑧 соответственно. Вероятность того, что молекулы газа
обладают скоростями, составляющие которых по осям координат лежат в
интервалах между 𝑣𝑥 и 𝑣𝑥 + 𝑑𝑣𝑥 , 𝑣𝑦 и 𝑣𝑦 + 𝑑𝑣𝑦 , 𝑣𝑥 и 𝑣𝑧 + 𝑑𝑣𝑧 равна : 𝑑𝑃𝑥,𝑦,𝑧 =
3
𝑚
𝑚𝑣 2
(2𝜋𝑘𝑇 )2 exp(− 2𝑘𝑇 )𝑑𝑣𝑥 𝑣𝑦 𝑣𝑧
Кол-во молекул из числа находящихся в единице
объема газа с компонентами скорости, попадающими в заданные
интервалы,
определится
следующим
образом
𝑑𝑛 =
𝑚
3
𝑚𝑣 2
𝑚
3
2
𝑚𝑣 2
𝑛(2𝜋𝑘𝑇 )2 exp(− 2𝑘𝑇 )𝑑𝑣𝑥 𝑑𝑣𝑦 𝑑𝑣𝑧 Перейдем в пространство скоростей, тогда
𝑑𝑛
𝑑𝑉
=
𝑛(2𝜋𝑘𝑇 ) exp(− 2𝑘𝑇 ) где 𝑑𝑉 = 𝑑𝑣𝑥 𝑑𝑣𝑦 𝑑𝑣𝑧 Полученное выражение не зависит от
направления скорости. Найдем ф-ю распределения молекул по
скоростям независимо от их направления. В интервал 𝑣, 𝑣 + 𝑑𝑣 попадут
молекулы, находящиеся в шаровом слое объемом 4𝜋𝑣 2 𝑑𝑣
𝑚
3
2
𝑚𝑣 2
или
𝑛(2𝜋𝑘𝑇 ) exp(− 2𝑘𝑇 )
молекул
𝑉
процессТ = 𝑐𝑜𝑛𝑠𝑡:𝐴12 = ∫𝑉 2 𝑝𝑑𝑉 = ∫𝑉 2
𝜈𝑅𝑇 ln(𝑉2 − 𝑉1 );
4)
адиабатический процесс 𝑑𝑄 = 0 ⟹ выполняется уравнение
𝑚𝑅𝑇
скорости, то есть скорости газовых молекл -𝑣𝑥2 – случайные величины. Более
точно случайные величины характеризует среднеквадратичная величина
⟨𝑣𝑥2 ⟩. Т.к. вектор скорости имеет 3 равноправные компоненты, то нельзя
выделить ни одну из этих компонент, и поэтому вместо ⟨𝑣𝑥2 ⟩ возьмем ⟨𝑣 2 ⟩.
𝑚
3
по
3
2 2
𝑚𝑣 2
Ф-я
𝑑𝑛 = 4𝜋𝑛(2𝜋𝑘𝑇 ) v exp(− 2𝑘𝑇 )𝑑𝑣
скоростям
𝑚𝑣 2
𝑚
4𝜋(2𝜋𝑘𝑇 )2 v 2 exp(− 2𝑘𝑇 Функция
–
з-н
Маквелла
распределения
𝑑𝑛
4𝜋𝑣 2𝑑𝑣
=
распределения
имеет
молекул
:
по
вид: 𝑓(𝑣) =
компоненте
скорости имеет вид
43 Распределение Больцмана. Распределение МаксвеллаБольцмана.
𝜇
𝑚
Заменив в барометрической формуле давление через nkT, 𝑅 = 𝑘 получим
𝑚𝑔ℎ
закон изменения с высотой числа молекул в единице объёма: 𝑛 = 𝑛0 𝑒 − 𝑘𝑇 ,
где 𝑚- масса 1-ой молекулы, k – постоянная Больцмана, 𝑛0 - число молекул
в единице объёма на высоте, равной 0, n – то же число на высоте ℎ. Из этой
формулы следует, что с понижением температуры число частиц на
высотах, отличных от нуля, убывает, обращаясь в 0 при Т=0. При высоких
температурах, напротив, n слабо убывает: все молекулы оказываются
распределёнными
по
высоте
почти
равномерно,
т.к.
каждое
распределение молекул по высоте устанавливается в результате 2-ух
тенденций: 1) притяжение молекул к земле mg стремиться расположить их
на поверхности земли; 2) тепловое движение kT стремиться разбросать
молекулы равномерно по высотам. На разной высоте молекула обладает
различным запасом потенциальной энергии: 𝑈 = 𝑚𝑔ℎ. Следовательно,
распределение молекул по высоте является и распределением их по
значениям потенциальной энергии. Объединив закон изменения с высотой
числа молекул в единице объёма формулу запаса потенциальной,
энергии получим распределение Больцмана:
𝑛1
𝑛2
=𝑒
𝑈 −𝑈
− 1 2
𝑘𝑇
,где 𝑛1 и 𝑛2 – число
молекул в точках, где потенциальная энергия имеет значения 𝑈1 и
𝑈2 .Больцман доказал, что распределение справедливо не только в случае
потенциального поля сил земного тяготения, но и в любом потенциальном
поле сил для совокупности любых одинаковых частиц, находящихся в
состоянии хаотического теплового движения. В то время как закон
Максвелла даёт распределение частиц по значениям кинетической
энергии, закон Больцмана даёт распределения частиц по значениям
потенциальной энергии. Распределения Максвелла и Больцмана можно
объединить в один закон Максвелла-Больцмана, согласно которому
содержащееся в единице объёма количество молекул, скорость которых
лежит между 𝑣 и 𝑣 + 𝑑𝑣, равно: 𝑑𝑛𝐸 = 𝑛0 4𝜋 (
𝑚
2𝜋𝑘𝑇
3
2
𝐸
) 𝑒 −𝑘𝑇 𝑣 2 𝑑𝑣.
54-56. Энтропия. Термодинамическая энтропияS, часто просто именуемая
энтропия, в химии и термодинамике является функцией состояния
термодинамической системы. Понятие энтропии было впервые введено
Рудольфом Клаузиусом, который определил изменение энтропии
термодинамической системы при обратимом процессе как отношение
изменения общего количества тепла ΔQ к величине абсолютной
температуры T (то есть изменение тепла при постоянной температуре):
∆𝑆 =
∆𝑄
𝑇
. Например, при температуре 0 °C, вода может находиться в жидком
состоянии и при незначительном внешнем воздействии начинает быстро
превращаться в лед, выделяя при этом некоторое количество теплоты. При
этом температура вещества так и остается 0 °C. Изменяется состояние
вещества, сопровождающееся изменением тепла, вследствие изменения
структуры. Эта формула применима только для изотермического
процесса (происходящего при постоянной температуре). Её обобщение
на случай произвольного квазистатического процесса выглядит так: 𝑑𝑆 =
𝛿𝑄
𝑇
,где dS — приращение (дифференциал) энтропии, а δQ — бесконечно
малое приращение количества теплоты. Необходимо обратить внимание
на то, что рассматриваемое термодинамическое определение
применимо только к квазистатическим процессам (состоящим из
непрерывно следующих друг за другом состояний равновесия). Энтропия –
аддитивная величина, т.е. энтропия системы равна сумме энтропий
отдельных её частей. Больцман установил связь энтропии с вероятностью
данного состояния. Позднее эту связь представил в виде формулы Планк:
𝑆 = 𝑘 ln(Ω), где константа k = 1,38×10−23 Дж/К названа Планком постоянной
Больцмана, а Ω — (термодинамическая вероятность) статистический вес
состояния, является числом возможных микросостояний (способов) с
помощью которых можно перейти в данное макроскопическое состояние
.Эта связь позволяет сформулировать II з-н термодинамики: наиболее
вероятным изменением энтропии является ее возрастание Этот постулат,
названный Альберт Эйнштейном принципом Больцмана, положил начало
статистической механики, которая описывает термодинамические
системы, используя статистическое поведение составляющих их
компонентов. Принцип Больцмана связывает микроскопические свойства
системы (Ω) с одним из её термодинамических свойств (S). Согласно
определению, энтропия является функцией состояния, то есть не зависит от
способа достижения этого состояния, а определяется параметрами этого
состояния. Так как Ω может быть только натуральным числом (1, 2, 3, …), то
энтропия Больцмана должна быть неотрицательной — исходя из свойств
логарифма. Энтропия в открытых системах:
В силу второго начала
термодинамики, энтропия Si замкнутой системы не может уменьшаться
(закон неубывания энтропии). Математически это можно записать
так: 𝑑𝑆𝑖 > 0 , индекс i обозначает так называемую внутреннюю энтропию,
соответствующую замкнутой системе. В открытой системе возможны
потоки тепла, как из системы, так и внутрь неё. В случае наличия потока
тепла в систему приходит количество тепла δQ1 при температуре T1 и
уходит количество тепла δQ2 при температуре T2. Приращение энтропии,
связанное
с
данными
тепловыми
потоками,
равно:
𝑑𝑆0 =
𝛿𝑄1
𝑇1
−
𝛿𝑄2
𝑇2
В
стационарных системах обычно δQ1 = δQ2, T1 >T2, так что dSo< 0. Поскольку
здесь изменение энтропии отрицательно, то часто употребляют выражение
«приток
негэнтропии»,
вместо
оттока
энтропии
из
системы.
Негэнтропияопределяется таким образом как обратная величина
энтропии. Суммарное изменение энтропии открытой системы будет
равно: dS = dSi + dSo. Если всё время dS> 0, то рост внутренней энтропии не
компенсируется притоком внешней негэнтропии, система движется к
ближайшему состоянию равновесия. Если dS = 0, то мы имеем
стационарный процесс с неизменной общей энтропией. В этом случае в
системе осуществляется некоторая внутренняя работа с генерацией
внутренней энтропии, которая преобразует, например, температуру T1
внешнего потока тепла в температуру T2 уходящего из системы потока
тепла. Измерение энтропии: В реальных экспериментах очень трудно
измерить энтропию системы. Техники измерения базируются на
термодинамическом определении энтропии и требуют экстремально
аккуратной калориметрии. Для упрощения мы будем исследовать
механическую систему, термодинамические состояния которой будут
определены через её объем V и давление P. Для измерения энтропии
определенного состояния мы должны сперва измерить теплоёмкость при
постоянных объёме и давлении (обозначенную CV и CP соответственно),
для успешного набора состояний между первоначальным состоянием и
требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T
согласно
𝛿𝑆
формуле:
𝐶𝑥 = 𝑇(𝛿𝑇)𝑥 ,
где
нижний
индекс
X
относится
к
постоянным объёму и давлению. Мы можем проинтегрировать для
получения изменения энтропии: ∆𝑆 = ∫
𝐶𝑥
𝑇
𝑑𝑇. Таким образом, мы можем
получить значение энтропии любого состояния (P,V) по отношению к
первоначальному состоянию (P0,V0). Точная формула зависит от нашего
выбора промежуточных состояний. Для примера, если первоначальное
состояние имеет такое же давление, как и конечное состояние, то 𝑆(𝑃, 𝑉) =
𝑇(𝑃,𝑉) 𝐶𝑝 (𝑃,𝑉(𝑇,𝑃))
𝑆(𝑃, 𝑉0 ) + ∫𝑇(𝑃,𝑉 )
0
𝑇
𝑑𝑇 В
добавление,
если
путь
между
первым
и
последним состояниями лежит сквозь любой фазовый переход первого
рода, скрытая теплота, ассоциированная с переходом, должна также
учитываться. Энтропия первоначального состояния должна быть определена
независимо. В идеальном варианте выбирается первоначальное
состояние как состояние при экстремально высокой температуре, при
которой система существует в виде газа. Энтропия в этом состоянии
подобна энтропии классического идеального газа плюс взнос от
молекулярных вращений и колебаний, которые могут быть определены
спектроскопически.
39.
Второе начало термодинамики. Цикл Карно. Второе начало
термодинамики — физический принцип, накладывающий ограничение на
направление процессов передачи тепла между телами. Второе начало
термодинамики
гласит,
переход
от
тепла
что
тела,
невозможен
менее
самопроизвольный
нагретого,
к
телу,
более
нагретому.Второе начало термодинамики запрещает так называемые
вечные двигатели второго рода, показывая, что коэффициент полезного
действия не может равняться единице, поскольку для кругового процесса
температура холодильника не должна равняться 0. Второе начало
термодинамики является постулатом, не доказываемым в рамках
термодинамики. Оно было создано на основе обобщения опытных фактов
и
получило
многочисленные
экспериментальные
подтверждения.
Существуют несколько эквивалентных формулировок второго начала
термодинамики:
Постулат
Клаузиуса:
«Невозможен
процесс,
единственным результатом которого являлась бы передача тепла от более
холодного тела к более горячему» (такой процесс называется процессом
Клаузиуса). Постулат Томсона (Кельвина): «Невозможен круговой процесс,
единственным результатом которого было бы производство работы за счет
охлаждения теплового резервуара» (такой процесс называется процессом
Томсона). Эквивалентность этих формулировок легко показать. В самом
деле, допустим, что постулат Клаузиуса неверен, то есть существует
процесс, единственным результатом которого была бы передача тепла от
более холодного тела к более горячему. Тогда возьмем два тела с
различной температурой (нагреватель и холодильник) и проведем
несколько циклов тепловой машины, забрав тепло Q1 у нагревателя, отдав
Q2 холодильнику и совершив при этом работу A = Q1 − Q2. После этого
воспользуемся процессом Клаузиуса и вернем тепло Q2 от холодильника
нагревателю. В результате получается, что мы совершили работу только за
счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже
неверен.С другой стороны, предположим, что неверен постулат Томсона.
Тогда можно отнять часть тепла у более холодного тела и превратить в
механическую работу. Эту работу можно превратить в тепло, например, с
помощью трения, нагрев более горячее тело. Значит, из неверности
постулата Томсона следует неверность постулата Клаузиуса.Таким
образом, постулаты Клаузиуса и Томсона эквивалентны. Другая
формулировка второго начала термодинамики основывается на понятии
энтропии: «Энтропия изолированной системы не может уменьшаться»
(закон не убывания энтропии). Такая формулировка основывается на
представлении об энтропии как о функции состояния системы, что также
должно быть постулировано. В состоянии с максимальной энтропией
макроскопические необратимые процессы (а процесс передачи тепла
всегда является необратимым из-за постулата Клаузиуса) невозможны.
Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина
Карно, работающая по этому циклу, обладает максимальным КПД из всех
машин, у которых максимальная и минимальная температуры
осуществляемого цикла совпадают соответственно с максимальной и
минимальной температурами цикла Карно. Состоит из 2 адиабатических и
2 изотермических процессов. Одним из важных свойств цикла Карно
является его обратимость: он может быть проведён как в прямом, так и в
обратном направлении, при этом энтропия адиабатически изолированной
(без теплообмена с окружающей средой) системы не меняется. Пусть
тепловая машина состоит из нагревателя с температурой TH, холодильника
с температурой TX и рабочего тела. Цикл Карно состоит из четырёх стадий:
Изотермическое расширение. В начале процесса рабочее тело имеет
температуру TH, то есть температуру нагревателя. Затем тело приводится в
контакт с нагревателем, который изотермически (при постоянной
температуре) передаёт ему количество теплоты QH. При этом объём
рабочего тела увеличивается. Адиабатическое (изоэнтропическое)
расширение. Рабочее тело отсоединяется от нагревателя и продолжает
расширяться без теплообмена с окружающей средой. При этом его
температура
уменьшается
до
температуры
холодильника.
Изотермическое сжатие. Рабочее тело, имеющее к тому времени
температуру TX, приводится в контакт с холодильником и начинает
изотермически сжиматься, отдавая холодильнику количество теплоты QX.
Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется
от холодильника и сжимается без теплообмена с окружающей средой.
При этом его температура увеличивается до температуры нагревателя.
При изотермических процессах температура остаётся постоянной, при
адиабатических отсутствует теплообмен, а значит, сохраняется энтропия
(поскольку при δQ = 0). Поэтому цикл Карно удобно представить в
координатах T и S (температура и энтропия). Отсюда коэффициент
полезного действия тепловой машины Карно равен: 𝜂 =
𝑄𝐻 −𝑄𝑥
𝑄𝐻
=
𝑇𝐻 −𝑇𝑥
𝑇𝐻
.
60. Третье начало термодинамики Первое и второе начало термодинамики
не позволяет определить значение энтропии при абсолютном нуле Т= 0º К.
На основании обобщения экспериментальных исследований свойств
различных веществ при сверх низких температурах был установлен закон,
устранивший указанный недостаток. Сформулировал его в 1906 г. Нернст и
называется он третьим началом термодинамики, или теоремой Нернста:
энтропия любой равновесной системы при абсолютном нуле температуры
может быть равна нулю. Следствием Третьего начала является то что,
невозможно охладить тело до абсолютного нуля (принцип недостижимости
абсолютного нуля температуры).