L19-5
advertisement
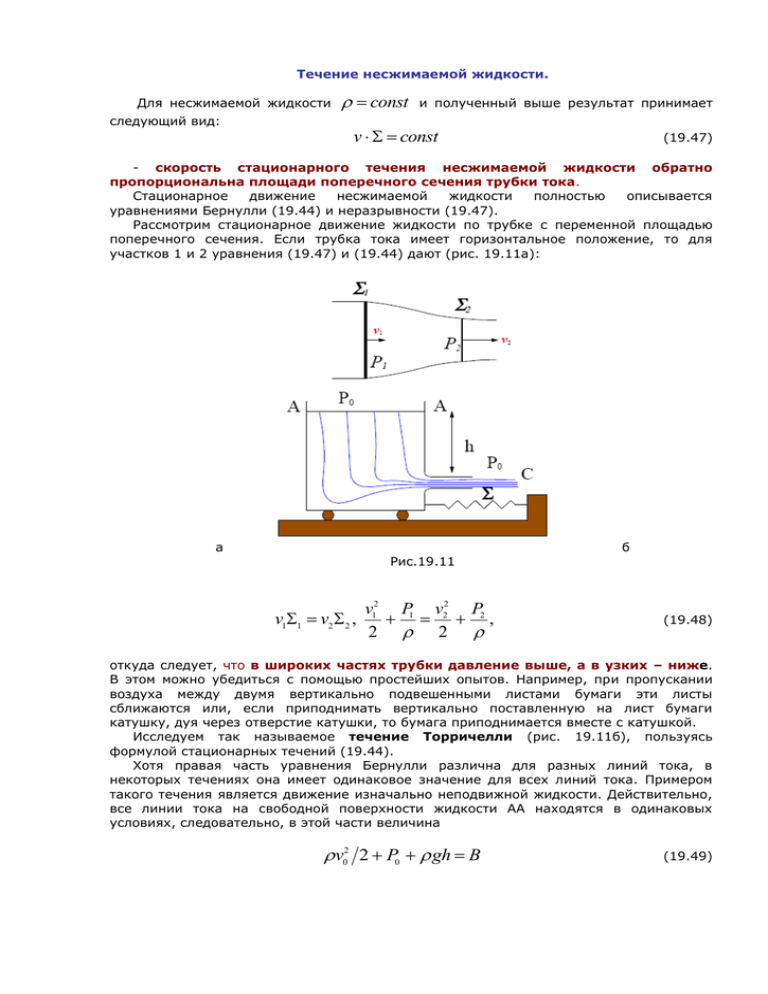
Течение несжимаемой жидкости. Для несжимаемой жидкости следующий вид: const и полученный выше результат принимает v const (19.47) - скорость стационарного течения несжимаемой жидкости обратно пропорциональна площади поперечного сечения трубки тока. Стационарное движение несжимаемой жидкости полностью описывается уравнениями Бернулли (19.44) и неразрывности (19.47). Рассмотрим стационарное движение жидкости по трубке с переменной площадью поперечного сечения. Если трубка тока имеет горизонтальное положение, то для участков 1 и 2 уравнения (19.47) и (19.44) дают (рис. 19.11а): а б Рис.19.11 v12 P1 v22 P2 v11 v2 2 , , 2 2 (19.48) откуда следует, что в широких частях трубки давление выше, а в узких – ниже. В этом можно убедиться с помощью простейших опытов. Например, при пропускании воздуха между двумя вертикально подвешенными листами бумаги эти листы сближаются или, если приподнимать вертикально поставленную на лист бумаги катушку, дуя через отверстие катушки, то бумага приподнимается вместе с катушкой. Исследуем так называемое течение Торричелли (рис. 19.11б), пользуясь формулой стационарных течений (19.44). Хотя правая часть уравнения Бернулли различна для разных линий тока, в некоторых течениях она имеет одинаковое значение для всех линий тока. Примером такого течения является движение изначально неподвижной жидкости. Действительно, все линии тока на свободной поверхности жидкости АА находятся в одинаковых условиях, следовательно, в этой части величина v02 2 P0 gh B (19.49) где P0 – внешнее атмосферное давление, – высота свободной поверхности жидкости h от уровня отверстия C, одинакова для всех линий и трубок тока. На выходе трубки C интеграл Бернулли имеет следующий вид: v2 2 P0 B, (19.50) где v – скорость жидкости на выходе из трубки. Пользуясь соотношениями (19.49) и (19.50), будем иметь v2 v02 2 gh . (19.51) Из условия неразрывности течения получаем v0 Площадь поперечного сечения трубки v. 0 (19.52) намного меньше формуле (19.51) можно пренебречь членом v02 . 0 , так что v0 v и в Значит, в узкой трубке скорость течения жидкости равна v 2 gh . (19.53) Эта формула выражает закон Торричелли о скорости струи жидкости под действием гидростатического давления. Заметим, что она совпадает с величиной скорости свободно падающего тела. Если рассматриваемая установка помещена на тележку, то она будет двигаться в направлении противоположном струе жидкости. Это, фактически, пример движения тела с переменной массой, где реактивная сила равна Fp u dm vdt v v 2 2 gh . dt dt Экспериментальным путем можно проверить выражение, полученное для реактивной силы. Это можно осуществить, прикрепив тележку к столу с помощью динамометра (рис. 19.11б). Вязкая жидкость. Уравнение Навье-Стокса. 1. Движение реальной жидкости отличается от движения жидкости, описываемой уравнениями (19.12), (19.18) и (19.6), которые удовлетворяют краевым условиям (19.19). В направлении касательном поверхности твердого тела (стенок) скорость идеальной жидкости может быть произвольной. Фактически, трубка, по которой течет жидкость, играет роль трубки тока и никакими касательными напряжениями не препятствует движению жидкости. Из этого следует, что любой, пусть даже маленький перепад давлений на концах горизонтальной трубки должен привести к возникновению ускоренного ( не стационарного) движения жидкости. В действительности из эксперимента получаются другие результаты: стационарный поток в горизонтальной трубке возможен только в случае убывания давления жидкости вдоль трубки. В этом можно убедиться с помощью простейшего опыта, в котором высоты столбов жидкости в манометрических трубках А, В, С показывают давление жидкости в соответствующих частях горизонтальной трубки (рис. 19.12а). Это явление можно объяснить предположением «сцепления» (прилипания) жидкости к стенкам трубки, также как наличием в жидкости внутреннего диссипативного взаимодействия трения. Предположение «сцепления» жидкости со стенками означает, что относительное движение жидкости на стенках (поверхности твердого тела) и самих стенок отсутствует. Если стенка неподвижна, то v 0. а (19.54) б Рис. 19.12 То есть, нулю равна не только нормальная составляющая скорости примыкающего слоя жидкости, но и тангенциальная (полная скорость). Наличие в жидкости диссипативного взаимодействия означает, что между соседними слоями самой жидкости действуют зависящие от их относительной скорости силы мокрого трения. Это силы внутреннего трения или вязкости жидкости. В том, что приведенные представления соответствуют действительности можно убедиться посредством эксперимента, схема которого приведена на рис. 19.12 б. После приведения во вращение диска В, спустя некоторое время в том же направлении начинает вращаться также диск А, подвешенный за упругую нить. Эксперимент дает тот же результат, как в жидкостях, так и в газах. Так как уравнение Эйлера – это дифференциальное уравнение первого порядка, то его решения не могут удовлетворять условию «сцепления» (19.54). Для этого необходимо, чтобы уравнение движения жидкости было дифференциальным уравнением хотя бы второго порядка. То есть, уравнение движения вязкой жидкости должно отличаться от уравнения Эйлера наличием членов, содержащих производные второго порядка по координатам от скорости. 2. Зависимость сил вязкости от производных относительной скорости было установлено еще Ньютоном. Пусть между двумя бесконечно длинными параллельными пластинами налита жидкость. Опыт показывает, что для приведения в движение этих пластин с постоянными скоростями силы F ,F u1 и u2 необходимо применить к ним постоянные (рис. 19.13а). Причем касательная сила, приходящаяся на единицу площади пластины f прямо пропорциональна относительной скорости пластин и обратно пропорциональна расстоянию f h между ними: u2 u1 , h где коэффициент пропорциональности (19.55) различен для различных жидкостей и называется динамической вязкостью жидкости. В СИ он имеет размерность кг м с . Используют также кинематическую вязкость: , которая имеет размерность м 2 (19.56) с. При данной температуре динамическая вязкость независима от давления, а кинематическая вязкость обратно пропорциональна давлению. В условиях комнатной температуры и нормального атмосферного давления для 1,8 103 кг м с , 1,5 105 м2 с , 1,5 103 кг м с , 1,2 103 м2 с . воздуха а а для глицерина б Рис.19.13 Продолжим обсуждение эксперимента, изображенного на рис. 19.13а. Так как при приложении к пластинам постоянных сил они двигаются с постоянными скоростями, то жидкость действует на пластины с силами F , F , уравновешивающими эти силы. Согласно третьему закону Ньютона пластины, в свою очередь, действуют на поверхностный слой жидкости с силами F ,F , обеспечивая условие «сцепления» жидкости: vx z1 u1 ; vx z2 u2 , (19.56) где выбор осей X и Z прямоугольной системы координат показан на рис. 19.9а. Мысленно разбив жидкость на бесконечно тонкие, параллельные пластинам слои и рассматривая стационарное движение каждого из них, можем утверждать, что единица площади любого слоя толщиной dz подвергается воздействию равных по величине и противоположно направленных тангенциальных напряжений xz dvx dz (19.57) Причем, сила трения, действующая на единичную площадь поверхности пластины это касательное напряжение жидкости на пластине, взятое с обратным знаком xz z z1 z z2 (19.58) Как и нормальные напряжения, так и тангенциальные напряжения равносильны объемной силе. Только в этом случае объемная сила имеет диссипативный характер. В случае произвольного движения вязкой несжимаемой жидкости ее единичный объем подвергается воздействию вязкой объемной силы (при const ) f вяз v (19.59) где – действие дифференцирования второго порядка по координатам. Оно называется оператором Лапласа и связано с следующим образом: . В прямоугольной системе координат 2 2 2 x 2 y 2 z 2 . (19.60) Добавив выражение (19.59) в правую часть уравнения Эйлера, получим уравнение движения вязкой несжимаемой жидкости v v v P v + f t (19.61) которое называется уравнением Навье-Стокса. В поле силы тяжести Земли уравнение Навье-Стокса имеет следующий вид: v 1 v v g P v . t (19.61´) Решения этого уравнения уже могут удовлетворять граничным условиям (19.54) «сцепления» жидкости к стенкам. 3. Уравнение неразрывности, являющееся математическим выражением закона сохранения массы, не зависит от того идеальная ли жидкость или вязкая и для вязкой жидкости имеет тот же вид. Естественно, что при наличии вязкости течение не может быть адиабатным, так как в жидкости постоянно имеет место явление превращения механической энергии в тепловую. Оно может привести также к неравномерному нагреванию жидкости, а последнее – к появлению дополнительного явления теплопередачи. Указанные явления учитываются уравнением энергетического баланса жидкости, которое заменяет ее уравнение состояния. Получение данного уравнения выходит за рамки нашего курса. В простейшем случае для несжимаемой жидкости оно имеет следующий вид: T v T T , t где – называется коэффициентом темперопроводности, а (19.62) – диссипация энергии, обусловленная вязкостью и которая является количеством энергии, преобразованного в единичном объеме за единицу времени. В неподвижной жидкости (19.62) дает уравнение теплопроводности T T , t (19.63) применимость которого в жидкостях, однако, ограничено, так как в жидкостях обычно перенос тепловой энергии сопровождается конвекцией теплопроводность в твердых телах (уравнение Фурье). v 0 . (19.63) описывает