Урок алгебры в 10 классе

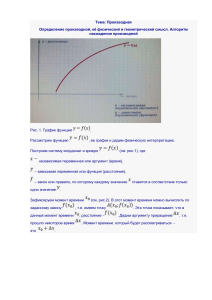
Ребята! Мы с вами начали изучение большой и важной темы “Производная”.
Запишите тему урока: “Определение производной”.
Математика в школе – это достаточно сложный предмет и самое главное для
учащихся – понять, зачем она нужна. Мы изучаем производную. А так ли это важно
в жизни? Давайте попробуем вместе в этом разобраться.
В начале урока мне хочется дать вам небольшую историческую справку.
Понятие «производная» возникло в XVII веке в связи с необходимостью решения
ряда задач из физики, механики и математики.
Великий французский математик Пьер Ферма в 1629 г. Научился находить
касательные к алгебраическим прямым.
В 1638г Ферма поделился этим открытием со своим земляком Рене Декартом,
который тоже занимался этой проблемой и нашел свой метод построения
касательных к алгебраическим кривым.
Ферма далеко продвинулся в применении дифференциальных методов. Он
использовал их не только для проведения касательных, но, к примеру, для
нахождения максимумов, вычисления площадей.
Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и
результаты в единую систему. Тем не менее, выдвинутые идеи не пропали в пустую.
Многие из них легли в основу нового метода математического анализа –
дифференциального исчисления.
«Дифференциальное исчисление - это описание окружающего нас мира,
выполненное на математическом языке. Производная помогает нам успешно решать
не только математические задачи, но и задачи практического характера в разных
областях науки и техники».
Основоположниками этого метода считаются Вильгельм Лейбниц (1646 – 1716)
и Исаак Ньютон (1642 – 1727).
Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат,
которым мы и пользуемся в настоящее время.
И. Ньютон в основном опирался на физическое представление о мгновенной
скорости движения, а Г. Лейбниц использовал понятие бесконечно малой.
С помощью диф. исчисления был решен целый ряд задач теоретической
механики, физики и астрономии. В частности, ученые предсказали возвращение
кометы Галлея, что было большим триумфом науки XVII века.
Очень многие великие ученые внесли свой вклад в зарождение и развитие диф.
исчисления. Среди них - Джеймс Грегори, Якоб Бернулли, Гийом Франсуа Лопиталь,
Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, который в 1797 г.ввел
термин «производная» и современные обозначения y’ , f ’ .
В настоящее время понятие производной находит большое применение в
логистике и коммерческой деятельности. Умение применять производную к
исследованию функции - важный элемент математической культуры.
Продолжить свой урок мне хочется словами Бориса Пастернака
Во всем мне хочется дойти
До самой сути.
В работе, в поисках пути,
В сердечной смуте.
До сущности протекших дней,
До их причины,
До оснований,
До корней, до сердцевины.
И сейчас мы постараемся дойти до самой сути определения производной и покажем
ее применение в различных областях знаний.
Рассмотрим задачи, приводимые к понятию производной.
Представим себе, что мы отправляемся в автомобильную поездку. Садясь в
машину, посмотрим на счетчик километража. Теперь в любой момент времени мы
сможем определить путь пройденный машиной. Скорость движения мы узнаем по
спидометру. А теперь попробуем решить ту же задачу, не выходя из дома.
Пусть по прямой на которой заданы начало отсчета, единица измерения (метр) и
направление, движется некоторое тело (материальная точка). Закон движения задан
формулой S=S(t). T – время в сек; S(t) – положение тела на прямой в момент
времени t по отношению к началу отсчета (в м). Найти скорость движения тела в
момент времени t (в м/с).
Решение.
Пусть в момент времени t тело находилось в т.М. ОМ=S(t). Дадим аргументу t
приращение и рассмотрим положение точки в момент времени
.
Значит за
секунд тело переместиться из т.М в т.Р
Найдем среднюю скорость движения тела за промежуток времени
Если
, то получим скорость в момент времени
- мгновенную скорость.
Задача о касательной к графику функции.
Чтобы составить наглядное представление о том, как провести касательную,
нужно вообразить себе, что к кривой, изготовленной из жесткого материала
(например, из проволоки), вы приставляете линейку так, чтобы она коснулась этой
кривой в выбранной точке. Если вы вырезаете из бумаги криволинейную фигуру, то
ножницы направлены по касательной к ее границе.
Постараемся перевести наглядное представление о касательной на более точный
язык. Будем считать, что кривая — это ломаная с очень большим числом маленьких
звеньев. Именно такая точка зрения была у создателей дифференциального
исчисления. В первом учебнике по анализу, написанном 300 лет назад
последователем Лейбница маркизом Лопиталем, дано следующее определение касательной: «Если продолжить одно из маленьких звеньев ломаной, составляющей
кривую линию, то эта продолженная таким образом сторона будет называться касательной к кривой»
Дан график функции
. На нем выбрана точка
, в этой точке
к графику проведена касательная. Найти угловой коэффициент касательной.
Дадим аргументу приращение
и рассмотрим т.Р
.Угловой коэффициент
секущей , т.е. тангенс угла наклона между секущей и осью Х
. Станем
приближать точку Р1 к Р. Положение секущей РР1 будет меняться, но с
приближением Р1 к Р начнет стабилизироваться. Предельное положение секущей
РР1 при стремлении точки Р1 к точке Р и будет касательной к кривой в точке Р.
При х  0 угловой коэффициен т секущей  к угловому
коэффициен ту касательной.
Две различные задачи привели к одной и той же математической модели –
пределу отношения приращения функции к приращению аргумента, при условии,
что приращение аргумента стремится к 0.
Дать определение производной.
Физический смысл производной – производная – это скорость изменения
функции.
Геометрический смысл производной – значение производной в точке касания –
угловой коэффициент касательной.
Дать алгоритм нахождения производной с помощью определения. (Записать в
тетрадь).
Проверить дом. задание №39.45. Записать производные полученных функций.
А сейчас рассмотрим задачи, которые также можно решить с помощью
производной.
Задача по химии
Пусть количество вещества, вступившего в химическую реакцию задается
2
зависимостью: р(t) = t /2 + 3t –3 (моль)
Найти скорость химической реакции через 3 секунды.
Понятие на языке
химии
Обозначение
Понятие на языке математики
Количество в-ва в
момент времени t0
p = p(t 0)
Функция
Интервал времени
∆t = t– t0
Приращение аргумента
Изменение количества
в-ва
∆p= p(t0+ ∆ t ) – p(t0)
Приращение функции
Средняя скорость
химической реакции
∆p/∆t
Отношение приращения функции
к приращению аргумента
Производная в биологии
По известной зависимости численности популяции x (t) определить относительный
прирост в момент времени t.
Понятие на языке
биологии
Обозначение
Понятие на языке
математики
Численность в момент
времени t1
x = x(t)
Интервал времени
∆t = t2 – t1
Приращение аргумента
Изменение численности
популяции
∆x = x(t2) – x(t1)
Приращение функции
Скорость изменения
численности популяции
Относительный прирост
в данный момент
Функция
Отношение приращения
функции к приращению
аргумента
∆x/∆t
Lim
t 0
∆x/∆t
Производная
Задача по географии:
Вывести формулу для вычисления численности населения на
ограниченной территории в момент времени t.
А мы с вами решим задачу №40.4.
В следующем году вы закончите школу и, наверное, каждый из вас уже сейчас
задумывается: «Куда пойти учиться? Кем стать?»
А нужно ли будет знание производной в вашей будущей профессии?
С такими задачами в наше время приходится иметь дело представителям самых
разных специальностей:
• Инженеры технологи стараются так организовать производство, чтобы
выпускалось как можно больше продукции;
• Конструкторы пытаются разработать прибор для космического корабля так,
чтобы масса прибора была наименьшей;
• Экономисты стараются спланировать связи завода с источниками сырья так,
чтобы транспортные расходы оказались минимальными.
Производная нашла широкое применение:
• а) в алгебре и началах анализа при исследовании функции и построении
графиков функций;
•
б) в физике при решении задач на нахождение скорости неравномерного
движения, плотности неоднородного тела и др.
•
в) в тригонометрии при вычислении тангенса угла наклона касательной к
кривой,
•
а также в геометрии, астрономии, аэродинамике, химии и экономике,
биологии и медицине.
«…нет ни одной области в математике, которая когда-либо не
окажется применимой к явлениям действительного мира…»
Н.И. Лобачевский
Значит изучать
производную нам нужно?
А сейчас давайте подведем итоги урока и оценим нашу работу на уроке.
Продолжите фразу:
«Сегодня на уроке я узнал…»
«Сегодня на уроке я научился…»
«Сегодня на уроке я познакомился…»
«Сегодня на уроке я повторил…»
«Сегодня на уроке я закрепил…»
А сейчас запишем Д/з: п.40, №40.3(б, в), №40.4(б, в)
Заканчивая свой урок, я поставлю проблемный вопрос: « Можно ли находить
производные, не используя определение? Существуют ли более удобные способы?»