Контрольная работа Вариант 6 Исходные данные: Функция

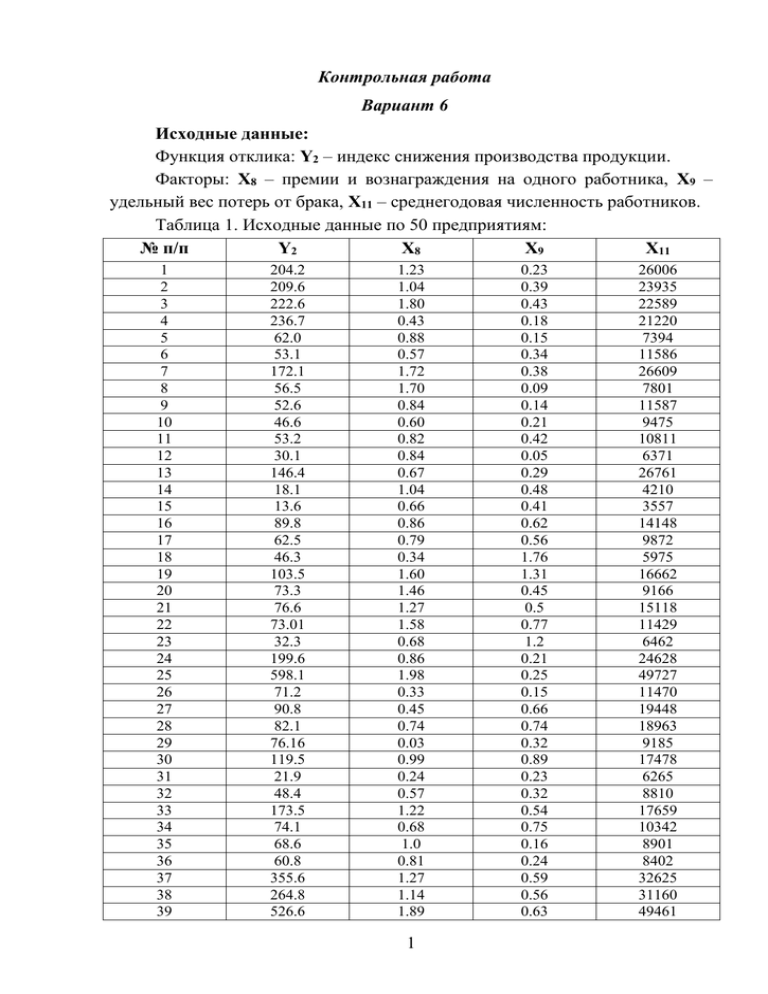
Контрольная работа
Вариант 6
Исходные данные:
Функция отклика: Y2 – индекс снижения производства продукции.
Факторы: X8 – премии и вознаграждения на одного работника, X9 –
удельный вес потерь от брака, X11 – среднегодовая численность работников.
Таблица 1. Исходные данные по 50 предприятиям:
№ п/п
Y2
X8
X9
X11
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
204.2
209.6
222.6
236.7
62.0
53.1
172.1
56.5
52.6
46.6
53.2
30.1
146.4
18.1
13.6
89.8
62.5
46.3
103.5
73.3
76.6
73.01
32.3
199.6
598.1
71.2
90.8
82.1
76.16
119.5
21.9
48.4
173.5
74.1
68.6
60.8
355.6
264.8
526.6
1.23
1.04
1.80
0.43
0.88
0.57
1.72
1.70
0.84
0.60
0.82
0.84
0.67
1.04
0.66
0.86
0.79
0.34
1.60
1.46
1.27
1.58
0.68
0.86
1.98
0.33
0.45
0.74
0.03
0.99
0.24
0.57
1.22
0.68
1.0
0.81
1.27
1.14
1.89
1
0.23
0.39
0.43
0.18
0.15
0.34
0.38
0.09
0.14
0.21
0.42
0.05
0.29
0.48
0.41
0.62
0.56
1.76
1.31
0.45
0.5
0.77
1.2
0.21
0.25
0.15
0.66
0.74
0.32
0.89
0.23
0.32
0.54
0.75
0.16
0.24
0.59
0.56
0.63
26006
23935
22589
21220
7394
11586
26609
7801
11587
9475
10811
6371
26761
4210
3557
14148
9872
5975
16662
9166
15118
11429
6462
24628
49727
11470
19448
18963
9185
17478
6265
8810
17659
10342
8901
8402
32625
31160
49461
40
41
42
43
44
45
46
47
48
49
50
118.6
37.1
57.7
51.6
64.7
48.3
15.0
87.5
108.4
267.3
34.2
0.67
0.96
0.67
0.98
1.16
0.54
1.23
0.78
1.16
4.44
1.06
1.1
0.39
0.73
0.28
0.1
0.68
0.87
0.49
0.16
0.85
0.13
13833
6391
11115
6555
11085
9484
3967
15283
20874
19418
3351
Решение:
1. Найдите оценки параметров линейной множественной регрессионной модели.
В данной задаче факторами являются X8, X9, X11 (далее будем обозначать x1, x2, x3), Y2 – функция отладки (обозначим как y).
Модель, соответствующая условию задачи:    0  1x1   2 x 2   3 x 3 .
В этом случае 0 ( x)  1 , 1 ( x)  x1 ,  2 ( x)  x2 , 3 ( x)  x3 .
Запишем исходные матрицы в Mathcad и найдем произведения матриц,
откуда матрица оценок коэффициентов равна:
 - 64.291 


1
 26.918 
1
T
T
T
,
B  A  F Y   F F   F Y   
- 2.172 


0
.
01


где F – матрица, составленная из 1 (1 столбец), а также коэффициентов Х (2-4
столбцы).
Таким образом, уравнение регрессии принимает вид:
~
y  64.291  26.918 x 1  2.172x 2  0.01x 3 (1).
2. Проверьте адекватность полученного уравнения регрессии.
Проверяем значимость уравнения регрессии в целом. Для этого вычисляем остаточную дисперсию:
 y
n
2
s ост

i1
~
y ( xi ) 
2
i
n  p 1
 1366 .25 ,
находим среднее значение функции отклика y  117.137 и общую дисперсию:
2
 y
n
s 2y 
i
y

2
 14209 .84 .
n 1
s 2y 14209 .84
Найдем отношение F  2 
 10.4 . По таблице определяем
s ост 1366 .25
i1
F1- (n  1; n  p  1)  F0.95 (49;47)  1.62 . В результате F  F0.95 (49;47 ) , то есть
критерий Фишера выполняется, значит уравнение множественной регрессии
(1) адекватно описывает результаты наблюдений.
3. Проверьте значимость коэффициентов уравнения регрессии и сделайте выводы.
Используем критерий Стьюдента:
t
bj
s bj
 t1 / 2 (n  p  1) .
Вычисляем погрешности коэффициентов регрессии (с учетом коэффициентов матрицы А-1):
s b1  1366 .25  0.056  8.716 , b1 /s b1  26.819 / 8.716  3.088 .
s b2  1366 .25  0.171  15.289 , b 2 /s b2  2.172 / 15.289  0.142 .
s b3  1366.25  2.259 10 10  5.56 10 4 , b 3 /s b3  0.01 / 5.56 10 4  18.472 .
По таблице определяем t1 / 2 (50  2  1)  t 0.975 (47)  2.01 .
Критерий значимости выполняется для коэффициентов  1 и  3 , следовательно, переменные x1 и x3 значимы. Для коэффициента  2 критерий значимости не выполняется, следовательно, переменная х2 может быть исключена из рассмотрения.
4. Исключите незначимые факторы из модели и найдите новые оценки
параметров линейной множественной регрессионной модели.
Исключаем из дальнейшего анализа переменную х2 и построим новое
уравнение регрессии. Для этого составим F – матрицу из 50 строк и 2 столбцов (x1 и x3).
Найдем матрицу оценок коэффициентов:
  65.294 


1
1
T
T
T
B  A  F Y   F F   F Y    26.788  .
 0.01 


3
Таким образом, уравнение регрессии принимает вид:
~
y  65.294  26.788 x 1  0.01x 3 (2).
5. Проверим адекватность полученного уравнения регрессии.
Проверяем значимость уравнения регрессии в целом. Для этого вычисляем остаточную дисперсию:
 y
n
2
s ост

Найдем отношение F 
i1
~
y ( xi ) 
2
i
n  p 1
s 2y
2
s ост

 1366 .83 .
14209 .84
 10.396 . По таблице определяем
1366 .83
F1- (n  1; n  p  1)  F0.95 (49;47)  1.62 . В результате F  F0.95 (49;47 ) , то есть
уравнение регрессии (2) адекватно описывает результаты наблюдений.
6. Определите остатки yi .
Определим разность между заданными величинами отклика и полученными в соответствии с уравнением регрессии и занесем их в таблицу:
Таблица 2. Остатки yi
~y
y
y
№ п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
204.2
209.6
222.6
236.7
62.0
53.1
172.1
56.5
52.6
46.6
53.2
30.1
146.4
18.1
13.6
89.8
62.5
46.3
103.5
73.3
76.6
73.01
32.3
234.673
208.319
214.858
164.102
34.198
68.935
253.991
60.343
76.178
48.064
67.675
22.623
227.424
5.792
-11.092
103.009
57.23
5.163
148.645
67.929
123.952
94.379
19.271
4
-30.473
1.281
7.742
72.598
27.802
-15.835
-81.891
-3.843
-23.578
-1.464
-14.475
7.477
-81.024
12.308
24.692
-13.209
5.27
41.137
-45.145
5.371
-47.352
-21.369
13.029
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
199.6
598.1
71.2
90.8
82.1
76.16
119.5
21.9
48.4
173.5
74.1
68.6
60.8
355.6
264.8
526.6
118.6
37.1
57.7
51.6
64.7
48.3
15.0
87.5
108.4
267.3
34.2
210.613
498.32
61.315
146.444
149.233
29.817
140.682
5.461
40.432
148.702
59.109
52.886
42.673
303.705
285.181
493.178
94.685
26.043
66.778
28.262
79.596
46.549
8.387
112.52
180.105
253.022
-2.492
-11.013
99.78
9.885
-55.644
-67.133
46.343
-21.182
16.439
7.968
24.798
14.991
15.714
18.127
51.895
-20.381
33.422
23.915
11.057
-9.078
23.338
-14.896
1.751
6.613
-25.02
-71.705
14.278
36.692
7. По критерию  2 проверить гипотезу о том, что остатки имеют нормальное распределение.
Объем выборки n = 50. Для проверки гипотезы найдем оценки математического ожидания и дисперсии:
2
1 50
1 50
2
y   yi  0 , s 
 yi  y   1311 .04 .
n  1 i1
n i1
Число
интервалов
группировки
определяем
по
формуле:
r  1  3.22 lg 50  6 . Размах выборки y max  y min  99.78  81.89  181 .67 .
Длина интервала группировки 181.67/6 ≈ 30.3. Результаты группировки помещаем во второй и третий столбцы таблицы, расширив первый и последний
интервалы:
Номер
i
ni
pi
np i
np i
ni  np i ni  npi 2
интервала
1
2
3
npi
-∞ – -51.6
-51.6 – -21.3
-21.3 – 9
5
5
19
0,077
0,201
0,320
3,83
10,06
16,00
5
3,83
10,06
16,00
1,170
-5,056
3,001
0,357
2,542
0,563
4
5
6
9 – 39.3
39.3 – 69.6
69.6 – +∞
Сумма
16
3
2
50
0,263
0,112
0,027
1,000
13,15
5,58
1,36
13,15
2,851
0,618
6,94
-1,943
0,544
50
50
0,024
4,624
Так как после объединения осталось r = 5 интервалов, а по выборке
определены оценки двух параметров, т.е. k = 2, то число степеней свободы r –
k – 1 = 5 – 2 – 1 = 2. По таблице квантилей распределения  2 находим
 21 (r - k -1)   2 0.95 (2)  5.99 . Из восьмого столбца определяем выборочное
значение статистики критерия  2 в  4,624 . Так как  2 в   2 0.95 (1) , то гипотезу
о нормальном распределении остатков следует принять.
8. Определите доверительный интервал для математического ожидания
s
s
t1 / 2 (n  1)  m  y 
t1 / 2 (n  1) .
остатков: y 
n
n
По таблице определяем t1 / 2 (50  2  1)  t 0.975 (47)  2.01 .
1311.04
1311.04
 2.01  m  0 
 2.01 .
50
50
 10.292  m  10.292 .
Таким образом, математическое ожидание остатков лежит с вероятностью 0,95 в интервале от -10,292 до +10,292.
0
9. Вычислите парные коэффициенты корреляции и запишите матрицу
коэффициентов корреляции.
Вычисляем коэффициенты корреляции с помощью функции corr(x,y) в
Mathcad.
10. Проверьте значимость парных коэффициентов корреляции и сделайте выводы.
Для проверки значимости парных коэффициентов корреляции вычисляем среднеквадратические погрешности и выборочные значения критерия
Стьюдента.
6
В результате:
ry,x1 / Sry,x1  3.837 , ry,x2 / Sry,x2  0.119 , ry,x3 / Sry,x3  19.603
rx1,x2 / Srx1,x2  0.601 , rx1,x3 / Srx1,x3  2.842 , rx2,x3 / Srx2,x3  0.185 .
Табличное значение критерия Стьюдента: t1 / 2 (50  2)  t 0.975 (48)  2.01 .
Отсюда можно сделать вывод, что значимыми являются коэффициенты
ry,x1 , ry,x3 , rx1,x3 . Таким образом, линейную корреляционную зависимость между переменными y и x1, y и x3, x1 и x3 можно считать существенной.
11. Вычислите коэффициент множественной корреляции и сделайте
выводы.
Для оценки тесноты линейной связи между величиной y и величинами
x1, x2, x3 вычисляем коэффициент множественной корреляции:
1
0.485  0.017 0.943
D
0.485
1
0.086
0.38
 0.017 0.086
1
 0.027
0.943
0.38  0.027
1
1
D 00  0.086
0.38
0.086
 0.078 ,
0.38
 0.027  0.846
1
 0.027
1
R  1  0.078 / 0.846  0.953 .
Таким образом, коэффициент множественной корреляции близок к 1,
что свидетельствует о значительной корреляционной связи между величиной
y и величинами x1, x2, x3.
12. Проверьте значимость коэффициента множественной корреляции
по критериям Стьюдента и Фишера.
Проверяем значимость коэффициента множественной корреляции по
критерию Стьюдента, для чего вычисляем среднеквадратическую погрешность и выборочное значение критерия Стьюдента:
SR  1  0.953 2 / 50  3  1  0.045 , R/S R  0.953 / 0.045  21.28 .
Табличное значение критерия Стьюдента
7
t1 / 2 (50  3  1)  t 0.975 (46)  2.01 .
Критерия Стьюдента выполняется, следовательно, множественный коэффициент корреляции является значимым.
Проверяем значимость коэффициента множественной корреляции по
критерию Фишера. Выборочное значении критерия:
0.953 2  (50  3  1)
F
 150 .93
1 - 0.953 2  3
cравниваем с табличным: F1- (3;50  3  1)  F0.95 (3;46)  2.81 . Таким образом,
выборочное значение больше табличного, а значит условие критерия Фишера
выполняется и коэффициент множественной корреляции является значимым.
13. Вычислите частные коэффициенты корреляции величин Y и Xi.
Для изучения влияния в отдельности каждого из фактора х на величину
отклика y вычисляем частные коэффициенты корреляции:
1
 0.017 0.943
0.485
0.086
0.38
D11   0.017
1
 0.027  0.111 , - А 01    0.017
1
 0.027  0.126
0.943  0.027
1
0.943  0.027
1
ry,x1/x2,x3  
1
D 22  0.485
0.943
0.485 0.943
D33  0.485
0.485
1
0.38
0.38  0.079 , - А 02    0.017 0.086  0.027  5.354  10 3
1
0.38
ry,x2/x1,x3  
1
A01
 0.411 .
D00 D11
1
0.943
1
A02
 0.021 .
D00 D22
0.485  0.017
0.485
1
0.086  0.756 , - А 03    0.017 0.086
1
 0.017 0.086
ry,x3/x1,x2  
0.38
1
0.943
0.38
0.086
1
 0.75
 0.027
A03
 0.938 .
D00 D33
14. Проверьте значимость частных коэффициентов корреляции и сделайте выводы.
Для проверки значимости частных коэффициентов корреляции вычисляем среднеквадратические погрешности и выборочное значение критерия
Стьюдента:
8
Sry,x1/x2, x3  1  0.4112 / 50  3  1  0.1344 ,
Sry,x2/x1, x3  1  0.0212 / 50  3  1  0.1474 ,
Sry,x3/x1,x2  1  0.938 2 / 50  3  1  0.0513 ,
ry,x1/x2,x3
Sry,x1/x2,x3
ry,x1/x2,x3
Sry,x1/x2,x3
ry,x1/x2, x3
Sry,x1/x2, x3

0.411
 3.055 .
0.1344

0.021
 0.141 .
0.1474

0.938
 18.274 .
0.0513
Табличное значение критерия Стьюдента
t1 / 2 (50  3  1)  t 0.975 (46)  2.01 .
Следовательно, согласно критерию Стьюдента, значимыми являются
частные коэффициенты корреляции ry,x1/x2, x3 и ry,x3/x1,x2 . Из полученных результатов видно, что зависимость между y и x1, y и x3 после устранения влияния
других величин можно считать существенной.
Вывод: Анализ полученных результатов показывает, что индекс снижения производства продукции зависит от премий и вознаграждений, а также
среднегодовой численности работников. В работе показана значимость данных факторов на индекс производства продукции.
9