Контрольная работа Вариант 9 Исходные данные: Функция

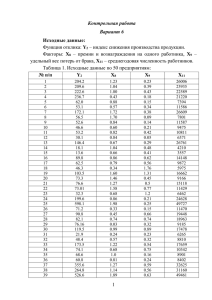
Контрольная работа
Вариант 9
Исходные данные:
Функция отклика: Y1 – производительность труда.
Факторы: X4 – трудоемкость единицы продукции, X6 – удельный вес
покупных изделий, X7 – коэффициент сменности оборудования.
Таблица 1. Исходные данные по 50 предприятиям:
№ п/п
Y1
X4
X6
X7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
9.26
9.38
12.11
10.81
9.35
9.87
8.17
9.12
5.88
6.3
6.22
5.49
6.5
6.61
4.32
7.37
7.02
8.25
8.15
8.72
6.64
8.1
5.52
9.37
13.17
6.67
5.68
5.22
10.02
8.16
2.78
6.48
10.44
7.65
8.77
7
11.06
9.02
13.28
0.23
0.24
0.19
0..17
0.23
0.43
0.31
0.26
0.49
0.36
0.37
0.43
0.35
0.38
0.42
0.3
0.32
0.25
0.31
0.26
0.37
0.29
0.34
0.23
0.17
0.29
0.41
0.41
0.22
0.29
0.51
0.36
0.23
0.26
0.27
0.29
0.01
0.02
0.18
1
0.4
0.26
0.4
0.5
0.4
0.19
0.25
0.44
0.17
0.39
0.33
0.25
0.32
0.02
0.06
0.15
0.08
0.2
0.2
0.3
0.24
0.1
0.11
0.47
0.53
0.34
0.2
0.24
0.54
0.4
0.2
0.64
0.42
0.27
0.37
0.38
0.35
0.42
0.32
1.37
1.49
1.44
1.42
1.35
1.39
1.16
1.27
1.16
1.25
1.13
1.1
1.15
1.23
1.39
1.38
1.35
1.42
1.37
1.41
1.35
1.48
1.24
1.40
1.45
1.40
1.28
1.33
1.22
1.28
1.47
1.27
1.51
1.46
1.27
1.43
1.5
1.35
1.41
40
41
42
43
44
45
46
47
48
49
50
9.27
6.7
6.69
9.42
7.24
5.39
5.61
5.59
6.57
6.54
4.23
0.25
0.31
0.38
0.24
0.31
0.42
0.51
0.31
0.37
0.16
0.18
0.33
0.29
0.3
0.56
0.42
0.26
0.16
0.45
0.31
0.08
0.68
1.47
1.35
1.40
1.2
1.15
1.09
1.26
1.36
1.15
1.87
1.17
Решение:
1. Найдите оценки параметров линейной множественной регрессионной модели.
В данной задаче факторами являются X4, X6, X7 (далее будем обозначать x1, x2, x3), Y1 – функция отладки (обозначим как y).
Модель, соответствующая условию задачи:    0  1x1   2 x 2   3 x 3 .
В этом случае 0 ( x)  1 , 1 ( x)  x1 ,  2 ( x)  x2 , 3 ( x)  x3 .
Запишем исходные матрицы в Mathcad:
 1 x1,1

 1 x 2,1
F   ... ...

 1 x 49,1
1 x
50,1

x1,2
x 2,2
...
x 49,2
x 50,2
x1,3   1
 
x 2,3   1
...    ...
 
x 49,3   1
x 50,3   1
1.37 
 y1   9.26 
  


0.24 0.26 1.49 
 y 2   9.38 
...
...
...  , Y   ...    ...  .
  


y
6.54
0.16 0.08 1.87 
 49  






0.18 0.68 1.17 
 y 50   6.23 
0.23
0.4
14.89 15.69
66.8 
 50
 387.18 




14.8
4.986
4.317
19.583
107.35

 T


, F Y 
.
A  FT F  

15.69 4.317
6
20.778
127.25 




 66.8 19.583 20.778 90.2 
 522.12 
 5.39 - 3.338 - 1.864 - 2.838 


3.338
3.488
1.379
1.397


Вычисляем обратную матрицу: A -1  
- 1.864 1.379 1.498 0.736 


2.838
1.397
0.736
1.64


Умножая матрицы, получаем матрицу оценок коэффициентов:
 9.803 



13
.
021

1


.
B  A1  F T Y   F T F   F T Y   
1.215 


 1.075 
2
Таким образом, уравнение регрессии принимает вид:
~
y  9.803  13.021x1  1.215x 2  1.075 x 3 (1).
2. Проверьте адекватность полученного уравнения регрессии.
Проверяем значимость уравнения регрессии в целом. Для этого вычисляем остаточную дисперсию:
 y
n
2
s ост

i 1
~
y ( xi )
2
i
n  p 1
 2.72 ,
находим среднее значение функции отклика y  7.74 и общую дисперсию:
 y
n
s 2y 
i 1
i
y
n 1

2
 4.97 .
s 2y 4.97
Найдем отношение F  2 
 1.827 . По таблице определяем
s ост 2.72
F1- (n  1; n  p  1)  F0.95 (49;47)  1.62 . В результате F  F0.95 (49;47) , то есть
условие критерия Фишера выполняется, а значит уравнение множественной
регрессии (1) адекватно описывает результаты наблюдений и является значимым.
3. Проверьте значимость коэффициентов уравнения регрессии и сделайте выводы.
Используем критерий Стьюдента:
t
bj
s bj
 t1 / 2 (n  p  1) .
Вычисляем погрешности коэффициентов регрессии (с учетом коэффициентов матрицы А-1):
s b1  2.72  3.488  3.08 , b1 /s b1  13.021 / 3.08  3.488 .
s b2  2.72  1.498  2.019 , b 2 /s b2  1.215 / 2.019  0.602 .
s b3  2.72  1.64  2.112 , b3 /s b3  1.075 / 2.112  0.51 .
По таблице определяем t1 / 2 (50  2  1)  t 0.975 (47)  2.01 .
Критерий значимости выполняется только для коэффициента  1 , следовательно, трудоемкость единицы продукции (переменная x1) является значимым фактором. Для коэффициентов  2 и  3 критерий значимости не вы3
полняется, следовательно, удельный вес покупных изделий и коэффициент
сменности оборудовании (переменные х2 и х3) могут быть исключены из рассмотрения.
4. Исключите незначимые факторы из модели и найдите новые оценки
параметров линейной множественной регрессионной модели.
Исключаем из дальнейшего анализа переменные х2 и х3 и построим новое уравнение регрессии. Для этого составим F – матрицу из 50 строк и 2
столбцов (единичного и x1).
 1 x1,1   1 0.23 

 

1
x
1
0.24



2,1 
 50 14.89  T
 387.18 



 , F Y  

F  ... ...  ... ...  , A  F T F  

 

14.89
4.986
107.35




 1 x 49,1   1 0.16 
1 x  

50,1 
 1 0.18 

Найдем матрицу оценок коэффициентов:
 12.035 
1
 .
B  A1  F T Y   F T F   F T Y   
  14.409 
Таким образом, уравнение регрессии принимает вид:
~
y  12.035  14.409 x1 (2).
5. Проверим адекватность полученного уравнения регрессии.
Проверяем значимость уравнения регрессии в целом. Для этого вычисляем остаточную дисперсию:
 y
n
2
s ост

i 1
~
y ( xi )
2
i
n  p 1
 2.746 .
s 2y
4.97
Найдем отношение F  2 
 1.81 . По таблице определяем
s ост 2.746
F1- (n  1; n  p  1)  F0.95 (49;47)  1.62 . В результате F  F0.95 (49;47) , то есть
уравнение регрессии (2) также является значимым, т.е. адекватно описывает
результаты наблюдений.
6. Определите остатки yi .
Определим разность между заданными величинами отклика и полученными в соответствии с уравнением регрессии и занесем их в таблицу:
4
Таблица 2. Остатки yi
№ п/п
y
~y
y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
9.26
9.38
12.11
10.81
9.35
9.87
8.17
9.12
5.88
6.3
6.22
5.49
6.5
6.61
4.32
7.37
7.02
8.25
8.15
8.72
6.64
8.1
5.52
9.37
13.17
6.67
5.68
5.22
10.02
8.16
2.78
6.48
10.44
7.65
8.77
7
11.06
9.02
13.28
9.27
6.7
6.69
9.42
7.24
5.39
5.61
8.721
8.576
9.297
9.585
8.721
5.839
7.568
8.288
4.974
6.847
6.703
5.839
6.991
6.559
5.983
7.712
7.424
8.432
7.568
8.288
6.703
7.856
7.136
8.721
9.585
7.856
6.127
6.127
8.865
7.856
4.686
6.847
8.721
8.288
8.144
7.856
11.89
11.746
9.441
8.432
7.568
6.559
8.576
7.568
5.983
4.686
0.539
0.804
2.813
1.225
0.629
4.031
0.602
0.832
0.906
-0.547
-0.483
-0.349
-0.491
0.051
-1.663
-0.342
-0.404
-0.182
0.582
0.432
-0.063
0.244
-1.616
0.649
3.585
-1.186
-0.447
-0.907
1.155
0.304
-1.906
-0.367
1.719
-0.638
0.626
-0.856
-0.83
-2.726
3.839
0.838
-0.868
0.131
0.844
-0.328
-0.593
0.924
5
47
48
49
50
5.59
6.57
6.54
4.23
7.568
6.703
9.729
9.441
-1.978
-0.133
-3.189
-5.211
7. По критерию  2 проверить гипотезу о том, что остатки имеют нормальное распределение.
Объем выборки n = 50. Для проверки гипотезы найдем оценки математического ожидания и дисперсии:
2
1 50
1 50
2
y   yi  0 , s 
 yi  y  2.634 .
n  1 i 1
n i1
Число интервалов группировки определяем по формуле: r  1  3.22 lg 50  6 .


Размах выборки ymax  ymin  4.031  5.211  9.242 . Длина интервала группировки 9.242/6 ≈ 1.54. Результаты группировки помещаем во второй и третий
столбцы таблицы, расширив первый и последний интервалы, а также объединим пятый и шестой интервал.
В четвертом столбце таблицы приведены вероятности pi, вычисленные
по формуле:
где  i ,  i 1
  x
  x
pi  PX   i   Ф i 1
  Ф i
, i  1,6 ,
s
s




- соответственно нижняя и верхняя граница интервалов, а Ф(х) –
функция распределения нормального закона.
  3.67  0 
 0
p1  P X  1   Ф
  Ф
  Ф 0.655   Ф    0.012
 2.634 
 2.634 
  2.13  0 
  3.67  0 
p2  PX  2   Ф
  Ф
  Ф 0.38  Ф 0.655   0.083
 2.634 
 31.35 
  0.59  0 
  2.13  0 
p3  P X  3   Ф
  Ф
  Ф 0.105   Ф 0.38  0.263
 2.634 
 2.634 
 0.95  0 
  0.59  0 
p4  P X  4   Ф
  Ф
  Ф0.17   Ф 0.105   0.363
 2.634 
 2.634 
 0 
 0.95  0 
p5  P X  5   Ф
  Ф
  Ф   Ф0.17   0.017 .
 2.634 
 31.35 
6
i
Номер
интервала
1
2
3
4
5
-∞ – -3.67
-3.67 – -2.13
-2.13 – -0.59
-0.59 – 0.95
0.95 – +∞
Сумма
ni
pi
np i
np i
ni  np i
1
2
11
29
7
50
0,012
0,083
0,263
0,363
0,279
1,000
0,59
4,14
13,17
18,14
13,95
50
4,73
13,17
18,14
13,95
50
-1,73
-2,17
10,86
-6,95
–
n
i
 npi 
npi
2
0,635
0,358
6,506
3,462
10,95
Так как после объединения осталось r = 4 интервалов, а по выборке
определены оценки двух параметров, т.е. k = 2, то число степеней свободы r –
k – 1 = 4 – 2 – 1 = 1. По таблице квантилей распределения  2 находим
 21 (r - k - 1)   2 0.95 (2)  3.84 . Из восьмого столбца определяем выборочное
значение статистики критерия  2 в  10,95 . Так как  2 в   2 0.95 (1) , то гипотезу
о нормальном распределении остатков следует отвергнуть.
8. Определите доверительный интервал для математического ожидания
s
s
t1 / 2 (n  1)  m  y 
t1 / 2 (n  1) .
остатков: y 
n
n
По таблице определяем t1 / 2 (50  2  1)  t 0.975 (47)  2.01 .
2.634
2.634
 2.01  m  0 
 2.01 .
50
50
 0.461  m  0.461 .
Таким образом, математическое ожидание остатков лежит с вероятностью 0,95 в интервале от -0,461 до +0,461.
0
9. Вычислите парные коэффициенты корреляции и запишите матрицу
коэффициентов корреляции.
Вычисляем коэффициенты корреляции в Mathcad:
ryx1 
Y  X1  Y  X1
Y  X2 Y  X2
 0.686 , ryx2 
 0.354 ,
 x  y
 x  y
1
ryx3 
2
Y  X3 Y  X3
X  X  X1  X 2
 0.317 , rx1x2  1 2
 0.46 ,
 x  y
 x  x
3
rx1x3 
1
2
X 1  X 3  X1  X 3
X  X  X2  X 3
 0.427 , rx2x3  2 3
 0.181 ,
 x  x
 x  x
1
3
2
7
3
где Y  X 1 , Y  X 2 , X 1  X 2 – средние значения взаимных произведений,
Y , X i – средние значения величин y и xi,  – среднеквадратическое откло-
нение величин, вычисленное по массиву в 50 значений для соответствующих
переменных.
 0.686 0.354 0.317 
 1 ryx1 ryx2 ryx3   1

 

1 rx1x2 rx1x3   - 0.686
1
- 0.46 - 0.427 
 rx1y
r 

.
rx2y rx2x1
1 rx2x3   0.354
- 0.46
1
- 0.181 

 

r
  0.317 - 0.427 - 0.181
r
r
1
1
x3y
x3x1
x3x2


 
10. Проверьте значимость парных коэффициентов корреляции и сделайте выводы.
Для проверки значимости парных коэффициентов корреляции вычисляем среднеквадратические погрешности и выборочные значения критерия
Стьюдента.
Рассчитаем матрицу Sri, j 
1  rij
2
 10 5 (добавка в виде малой величи-
n2
ны нужна для того, чтобы значение матрицы не было равно 0 для ненужных
элементов) и матрицу
rij
Sri, j
.
6.526 2.62 2.319 
 10 5 0.105 0.135 0.137 
 10 5




5
5
r
0
.
105
10
0
.
128
0
.
131
6
.
526
10
3
.
584
3
.
273

 ij 

Sri, j  

,
.
5
5

0.135 0.128 10
0.142 Sri, j
2.62 3.584 10
1.272 




 0.137 0.131 0.142 10 5 
 2.319 3.273 1.272 10 5 




В результате:
ry,x1 / Sry,x1  6.526 , ry,x2 / Sry,x2  2.62 ,
ry,x3 / Sry,x3  2.319
rx1, x2 / Srx1, x2  3.584 , rx1, x3 / Srx1, x3  3.273 , rx2, x3 / Srx2, x3  1.272 .
Табличное значение критерия Стьюдента: t1 / 2 (50  2)  t 0.975 (48)  2.01 .
Отсюда можно сделать вывод, что значимыми являются все коэффициенты парной корреляции за исключением коэффициента корреляции между
удельным весом покупных изделий и коэффициентом сменности оборудования ( rx2, x3 ), что говорит о несущественной связи этих переменных и существенной связи остальных пар переменных.
8
11. Вычислите коэффициент множественной корреляции и сделайте
выводы.
Для оценки тесноты линейной связи между величиной y и величинами
x1, x2, x3 вычисляем коэффициент множественной корреляции:
1
 0.686 0.354
0.317
D
 0.686
0.354
0.317
 0.46
1
 0.427
 0.46
1
 0.181
 0.427  0.181
1
1
D 00   0.46
 0.46
1
 0.427  0.181
 0.624 ,
 0.427
 0.181  0.503
1
R  1  0.503 / 0.624  0.689 .
Таким образом, коэффициент множественной корреляции больше 0,5,
что свидетельствует о средней корреляционной связи между производительностью труда, трудоемкостью продукции, удельным весом покупных изделий и коэффициентом сменности оборудования.
12. Проверьте значимость коэффициента множественной корреляции
по критериям Стьюдента и Фишера.
Проверяем значимость коэффициента множественной корреляции по
критерию Стьюдента, для чего вычисляем среднеквадратическую погрешность и выборочное значение критерия Стьюдента:
SR  1  0.689 2 / 50  3  1  0.107 , R/S R  0.689 / 0.107  6.451 .
Табличное значение критерия Стьюдента
t1 / 2 (50  3  1)  t 0.975 (46)  2.01 .
Критерия Стьюдента выполняется, следовательно, множественный коэффициент корреляции является значимым.
Проверяем значимость коэффициента множественной корреляции по
критерию Фишера. Выборочное значении критерия:
0.689 2  (50  3  1)
F
 13.87
1 - 0.689 2  3
cравниваем с табличным: F1- (3;50  3  1)  F0.95 (3;46)  2.81 . Таким образом,
выборочное значение больше табличного, а значит условие критерия Фишера
выполняется и с точки зрения данного критерия коэффициент множественной корреляции можно считать значимым.
9
13. Вычислите частные коэффициенты корреляции величин Y и Xi.
Для изучения влияния в отдельности каждого из фактора х на величину
отклика y вычисляем частные коэффициенты корреляции:
1
0.354
D11  0.354
 0.686
0.317
 0.181  0.701 , - А 01   0.354
0.317  0.181
1
0.317
 0.46
1
ry,x1/x2, x3  
1
D 22   0.686
0.317
1
 0.181
 0.686
0.317
 0.427  0.432 , - А 02   0.354
0.317
 0.427
1
1
 0.427
 0.427
 0.181  0.041
1
A02
 0.087 .
D00 D22
 0.686
1
 0.46
ry,x3/x1, x2  
1
 0.46
1
D 33   0.686
0.354
 0.181  0.312
1
A01
 0.525 .
D00 D11
 0.686
ry,x2/x1, x3  
 0.427
 0.686
0.354
 0.46  0.416 , - А 03   0.354
1
1
 0.46
 0.46
1
 0.034
 0.427  0.181
0.317
A03
 0.074 .
D00 D33
14. Проверьте значимость частных коэффициентов корреляции и сделайте выводы.
Для проверки значимости частных коэффициентов корреляции вычисляем среднеквадратические погрешности и выборочное значение критерия
Стьюдента:
Sry,x1/x2, x3  1  0.525 2 / 50  3  1  0.1255 ,
Sry,x2/x1, x3  1  0.087 2 / 50  3  1  0.1468 ,
Sry,x3/x1, x2  1  0.074 2 / 50  3  1  0.147 ,
ry,x1/x2, x3
Sry,x1/x2, x3
ry,x1/x2, x3
Sry,x1/x2, x3
ry,x1/x2, x3
Sry,x1/x2, x3

0.525
 4.182 .
0.1255

0.087
 0.596 .
0.1468

0.074
 0.504 .
0.147
Табличное значение критерия Стьюдента
t1 / 2 (50  3  1)  t 0.975 (46)  2.01 .
Следовательно, согласно критерию Стьюдента, значимым является
только частный коэффициент корреляции ry,x1/x2, x3 , отражающий зависимость
10
между производительностью труда и трудоемкостью единицы продукции
при отсутствии влияния удельного веса покупных изделий и коэффициента
сменности оборудования
Вывод: Анализ влияния производственных факторов на производительность труда показал, что последний существенно зависит от трудоемкости единицы продукции и не зависит существенно от удельного веса покупных изделий и коэффициента сменности оборудования. При этом трудоемкость единицы продукции можно считать статистически значимым фактором. Построенное уравнение регрессии зависимости производительности
труда от трудоемкости единицы продукции является статистически значимым.
11