Шар
advertisement
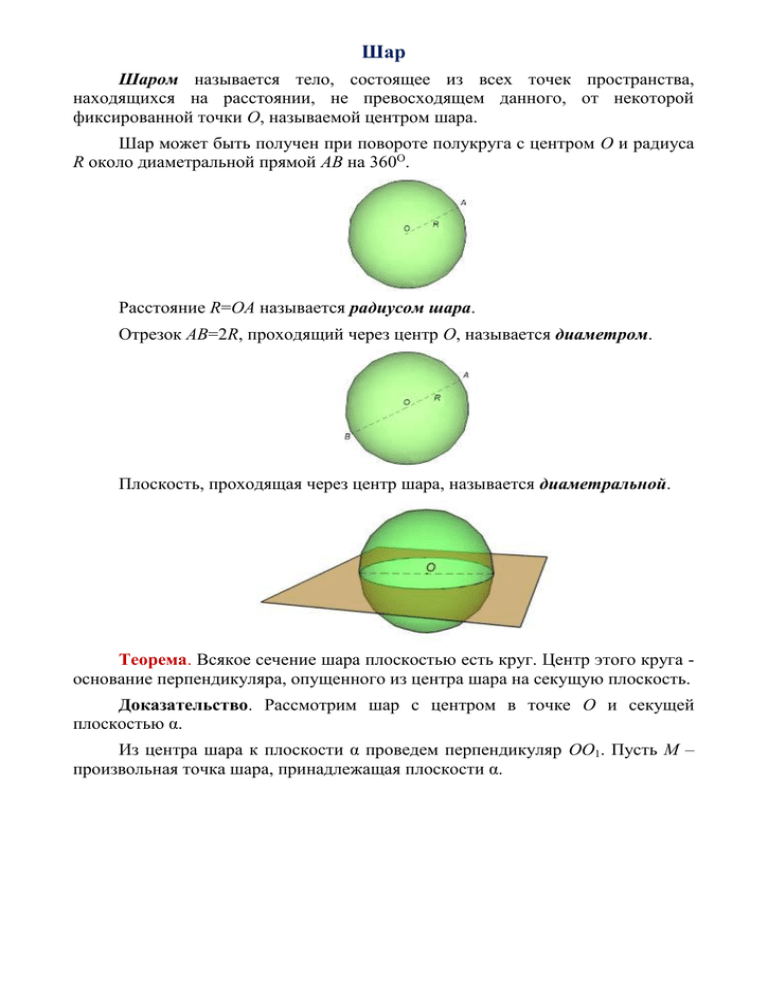
Шар Шаром называется тело, состоящее из всех точек пространства, находящихся на расстоянии, не превосходящем данного, от некоторой фиксированной точки О, называемой центром шара. Шар может быть получен при повороте полукруга с центром О и радиуса R около диаметральной прямой АВ на 360О. Расстояние R=ОА называется радиусом шара. Отрезок АВ=2R, проходящий через центр О, называется диаметром. Плоскость, проходящая через центр шара, называется диаметральной. Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга основание перпендикуляра, опущенного из центра шара на секущую плоскость. Доказательство. Рассмотрим шар с центром в точке О и секущей плоскостью α. Из центра шара к плоскости α проведем перпендикуляр ОО1. Пусть М – произвольная точка шара, принадлежащая плоскости α. Из прямоугольного треугольника ОО1М по теореме Пифагора получаем ОМ =О1О2+О1М2. 2 Так как ОМR, то О1М R2 O1O2 . Это значит, что любая точка М сечения шара плоскостью α находится на расстоянии, не большем R2 O1O2 от точки О1, т.е. принадлежит кругу с центром О1, радиус которого R1= R2 O1O2 . Обратно, любая точка М этого круга принадлежит шару. Следовательно, любое сечение шара плоскостью есть круг с центром в точке О1, являющейся основанием перпендикуляра, проведенного из центра шара к секущей плоскости. Теорема доказана. Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии. Доказательство. Пусть М – произвольная точка шара и α – его диаметральная плоскость. Построим точку М1, симметричную точке М относительно плоскости α. Отрезок ММ1 перпендикулярен к плоскости α и пересекает ее в некоторой точке А, причем АМ=АМ1. Из равенства прямоугольных треугольников ОАМ и ОАМ1 следует, что ОМ=ОМ1. Поскольку ОМR, то ОМ1R, т.е. точка М1, симметричная точке М относительно плоскости α, принадлежит шару. Пусть М2 – точка симметричная точке М относительно центра шара. В этом случае ОМ=ОМ2. так как ОМR, то ОМ2R, т.е. точка М2 принадлежит шару. Теорема доказана. Принцип Кавальери. Если две фигуры Ф1 и Ф2 можно расположить в пространстве так, что в сечениях их плоскостями, параллельными одной и той же плоскости, получаются фигуры F1 и F2 одинаковой площади, то объемы исходных пространственных фигур равны. Для обоснования этого принципа представим фигуры Ф1 и Ф2, составленными из тонких слоев одинаковой толщины, которые получаются при пересечении фигур Ф1 и Ф2 плоскостями, параллельными некоторой заданной плоскости. Так как соответствующие слои имеют одинаковую площадь и толщину, то их объемы равны. Поскольку объемы фигур равны сумме объемов составляющих их слоев, то равны объемы и самих фигур. 4 3 Теорема. Объем шара вычисляется по формуле V= R3, где R – радиус шара. Доказательство. Пусть дан полушар радиуса R, большой круг которого расположен на плоскости α. Рассмотрим цилиндр, основание которого - круг радиуса R, расположенный в той же плоскости, и высота которого равна R. В цилиндр впишем конус, основанием которого будет верхнее основание цилиндра, а вершиной - центр нижнего основания цилиндра. Докажем, что фигура, состоящая из точек цилиндра, не попавших внутрь конуса, и данный полушар имеют равные объемы. Проведем плоскость β, параллельную плоскости α, на расстоянии x от нее, 0<x<R. В сечении полушара этой плоскостью получим круг радиуса R2-x2 и площади (R2-x2). В сечении другой фигуры получается кольцо, радиус внутреннего круга в котором равен x, а внешнего – R. Площадь этого кольца равна R2-x2 и, следовательно, равна площади сечения полушара. Из принципа Кавальери следует, что полушар и построенная фигура имеют равные объемы. Объем полушара равен разности объемов цилиндра и конуса, т.е. R2H2 3 1 3 R2H= R2H. Поскольку высота конуса и цилиндра Н=R, то разность их объемов равна 2 R3. 3 Объем шара вдвое больше объема полушара и, следовательно, выражается формулой 4 R3. 3 Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Любая плоскость рассекает шар на два шаровых сегмента. Круг (О; ОС) – основание шаровых сегментов, АО и ВО – их высоты. Объем шарового сегмента находится по формуле: Vш.сегм=Н2(R-H/3), где Н – высота шарового сегмента, R – радиус основания. Сегментной поверхностью называется часть шаровой поверхности, отсекаемая от нее какой-нибудь плоскостью. Отрезок радиуса, перпендикулярного плоскости сечения, заключенный между шаровой поверхностью и плоскостью, называется высотой сегментной поверхности. Площадь сегментной поверхности вычисляется по формуле Sсег=2RH. Шаровым поясом называется часть шаровой поверхности, заключенная между двумя параллельными секущими плоскостями. Расстояние между этими плоскостями называется высотой шарового пояса. Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар. Круги с центрами О1 и О2 – основания шарового слоя, О1О2 – высота. Объем шарового слоя можно найти как разность между объемом шара и объемом двух отсекаемых сегментов. Площадь поверхности шарового пояса вычисляется по формуле Sш.п=2RH. Часть шаровой поверхности, принадлежащая шаровому слою, называется шаровым поясом. Шаровым сектором называется тело, состоящее из суммы или разности шарового сегмента и конуса с вершиной центре шара, имеющих общее основание (сумма, если шаровой сегмент меньше полушара, разность, если больше). АО, ОВ – высоты секторов и соответствующих им сегментов. 1 3 Объем шарового сектора вычисляется по формуле: Vш.сект= Sш.пR= R2H, где R – радиус основания, Н – высота шарового сектора. 2 3 Площадь полной поверхности шарового сектора вычисляется по формуле Sш.сек=R(2H+ 2RH H 2 ) Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания. Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания. Доказательство. Рассмотрим плоскость α, касательную к шару, и точку А – точку касания. Пусть М – произвольная точка плоскости α, отличная от А. Поскольку ОА – перпендикуляр, а ОМ – наклонная то ОМ>ОА=R, где R – радиус шара. Неравенство ОМ>R означает, что точка М шару не принадлежит. Теорема доказана. Прямая, проходящая через точку А шаровой поверхности перпендикулярно радиусу, проведенному в эту точку, называется касательной. Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причем все они лежат в касательной плоскости шара. Доказательство. Если плоскость α касается шара в точке А, то любая прямая в плоскости α, проходящая через точку А, перпендикулярная радиусу ОА, т.е. является касательной. Любая касательная, проходящая через точку А, перпендикулярна к радиусу ОА, и, следовательно, лежит в плоскости α. Теорема доказана. Примеры решения задач Задача № 1. Найдите объем шара, если длина окружности сечения шара плоскостью находящейся на расстоянии 9 см от центра равна 24 см. Дано: L=24 см, СО=9 см Найти: V Решение: 4 3 Объем шара вычисляется по формуле V= R2. Из прямоугольного треугольника ОСТ: R=ОТ= ОС 2 ТС 2 . ТС – радиус сечения. L=2ТС. Отсюда ТС=L/2=12 см. Следовательно, ОТ= ОС 2 ТС 2 =15 см. Отсюда V=4R2/3=4500 см3. Ответ: 4500 см3 Задача № 2. Сечение шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144 см2 и 25 cм2. Вычислите радиус шара, если расстояние между параллельными плоскостями равно 17 см. Дано: S1=144 см2, S2=25 cм2, ВС=17 см. Найти: R Решение: Площадь сечений вычисляется по формуле S=R2, где R – радиус сечения, следовательно радиусы сечений СТ=12 см, ВМ=5 см. Из прямоугольных треугольников ОСТ и ОВМ: ОC= ОТ 2 ТС 2 , ОВ= ОМ 2 ВМ 2 . ОМ=ОТ=R. ОС+ОВ=17.3 Отсюда ОТ 2 ТС 2 + ОМ 2 ВМ 2 = R 2 ТС 2 + R2 ВМ 2 =17 см. Решив полученное уравнение, получаем R=13 см. Ответ: 13 см Задача № 3. TABCD – правильная четырехугольная пирамида, апофема которой равна 10 см, а длина стороны основания равна 12 см. Вычислите радиус шара, вписанного в пирамиду. Дано: TABCD – правильная четырехугольная пирамида, AD=12 см,TF=10 см Найти: PO Решение: Пусть треугольник TKF – сечение пирамиды плоскостью, проходящей через высоту ТО и перпендикулярной стороне основания DC. Тогда центр Р шара совпадает с центром окружности, вписанной в треугольник TKF. Следовательно, радиус сферы равен радиусу окружности, вписанной в треугольник TKF. Пусть точка Е – точка касания окружности и стороны TF. Тогда PF – биссектриса угла OFT, а, значит, ОР:РТ=OF:TF. Так как OF=KF/2=6 см и TF=10 см, то ОР:РТ=3:5. Пусть ОР=3х, а ТР=5х. Тогда ТО=8х. Из уравнения 8х=8 находим х=1. Следовательно, РО=3х=3 см. Ответ: 3 см Задача № 4. Правильная треугольная призма вписана в шар. Вычислите радиус шара, если длина стороны основания призмы равна 6√3 см, а длина бокового ребра призмы равна 16 см. Дано: АА1=16 см, А1С1=6√3 см. Найти: ОО1 Решение: Пусть АВСА1В1С1 – правильная треугольная призма, вписанная в шар. Точка О – центр шара, точка О1 – центр окружности, по которой плоскость А1В1С1 пересекает шар. В прямоугольном треугольнике А1О1О (А1О1О=90о, ОО1=А1А/2=8 см) длина гипотенузы А1О= ОO12 A1O12 = 64 A1O12 . Треугольник А1В1С1 – равносторонний. Следовательно, А1О1=2A1Т/3 (точка Т – середина отрезка С1В1). Так как A1Т=А1С1√3/2=9 см, то А1О1=6 см. Теперь находим А1О= 64 A1O12 =10 см. Ответ: 10 см Задача № 5. Шар, диаметр которого равен 13 см, пересекается плоскостью, перпендикулярной диаметру шара РТ. Найдите отношение объемов пирамид POFK и TOFK, где точки F и К лежат на окружности с центром О и радиусом 6 см, по которой плоскость пересекает границу шара. Дано: РТ=13 см, ОК=OF=6 см. Найти: VPOFK/VTOFK Решение: Объемы пирамид POFK и TOFK находятся по формулам: VPOFK=SOFKPO/3, VTOFK=SOFKOT/3. Следовательно, VPOFK/VTOFK=РО/OT. Пусть РО=х, тогда ТО=13-х. В прямоугольном треугольнике PFT (PFT=90о, так как он опирается на диаметр большой окружности) имеем OF2=POTO, 36=х(13-х). Отсюда х=4 или х=9. Если РО= 4 см, то , VPOFK/VTOFK=4/9, а если РО=9 см, то VPOFK/VTOFK=9/4. Ответ: 4/9 или 9/4 Задания для самостоятельной работы Вариант 1 1. Используя рисунок, укажите радиус шара… 1) АВ 2) ОС 3) ОА 2. Как называется плоскость, проходящая через центр шара… 1) Секущая 2) Касательная 3) Диаметральная 3. Объем шара вычисляется по формуле… 1) 4R2/3 2) R3/3 3) 4R3/3 4. Чему равен диаметр шара, если его радиус 14 см… 1) 7; 2) 14; 3) 28; 5. Найдите объем шара, если его диаметр равен 6 см. 6. Вычислите радиус шара, если его центр О находится на расстоянии 4 см от центра С круга, полученного в сечении, а радиус этого круга равен 3 см. 7. Через точку, делящую радиус шара пополам, проведена секущая плоскость, перпендикулярная этому радиусу. Вычислите площадь получившегося сечения, если радиус шара равен 4 см. 8. Плоскость, перпендикулярная диаметру шара, делит его на отрезки длиной 4 см и 25 см. Вычислите площадь сечения шара данной плоскостью. 9. Вершиной конуса служит центр О шара, а его основанием сечение шара плоскостью. Вычислите площадь боковой поверхности конуса, если площадь граничной сферы равна 16 см2, а радиус сечения равен 1 см. 10. Металлический шар переплавлен в 27 равных между собой шаров. Во сколько раз увеличилась при этом общая поверхность? Вариант 2 1. Используя рисунок, укажите диаметр шара… 1) АВ 2) ВС 3) ВО 2. Любая плоскость пересекает поверхность шара по… 1) Кругу 2) Прямой 3) Окружности 3. Объем шарового сегмента вычисляется по формуле… 1) R3/3 2) Н2(R-H/3) 3) Н2(R-H) 4. Чему радиус шара, если его диаметр 36 см… 1) 6; 2) 18; 3) 9; 5. Найдите объем шара, если его радиус равен 6 см. 6. Плоскость пересекает шар по кругу радиуса 3 см. Вычислите расстояние от центра шара до секущей плоскости, если радиус шара равен 6 см. 7. Диаметр шара равен 25 см. Точка В поверхности шара находится на расстоянии 15 см от одного из концов диаметра шара. Вычислите площадь сечения шара плоскостью, проходящей через точку В и перпендикулярной диаметру. 8. Длина общей хорды двух взаимно перпендикулярных сечений шара равна 16 см. Вычислите площадь большого круга данного шара, если площади сечений равны 185 см2 и 320 см2. 9. Определить высоту шарового сектора, объем которого равен 512 см3, а сегментная поверхность равна 96 см2. 10. В шаре радиусом 15 см через его центр просверлено отверстие радиусом 9 см. Найдите объем полученной фигуры. Вариант 3 1. Используя рисунок, укажите высоту шарового сегмента … 1) ОА 2) ОС 3) СТ 2. Любое сечение шара является… 1) Окружностью 2) Кругом 3) Эллипсом 3. Объем шарового сектора вычисляется по формуле… 1) Н2(R-H/3) 2) 2R2H/3 3) 2R2H 4. Чему равен радиус шара, если площадь большого круга равна 81 см2… 1) 3; 2) 6; 3) 9; 5. Чему равен диаметр шара, если его объем равен 288 см3? 6. Шар радиуса 10 см пересечен плоскостью, находящейся на расстоянии 8 см от центра. Вычислите площадь сечения шара данной плоскостью. 7. Диаметр шара 52 см, а секущая плоскость удалена от его центра на 10 см. Вычислите площадь круга, полученного при пересечении шара и плоскости. 8. Диаметр шара разделен на три части в отношении 1:3:2 и через точки деления проведены перпендикулярные ему плоскости. Вычислите радиус шара, если сумма площадей сечений равна 52 см2. 9. В шаре проведены два взаимно перпендикулярных сечения на расстоянии 8 см и 12 см от центра. Вычислите радиус шара, если длина общей хорды сечений равна 18 см. 10. Три шара радиусом 6 см лежат на плоскости и касаются друг друга. Радиус шара, касающегося трех данных шаров и плоскости равен. Вариант 4 1. Используя рисунок, укажите радиус шарового сектора… 1) СТ 2) ОА 3) ОС 2. Отрезок, лежащий на поверхности шара и проходящий через его центр, называется… 1) Радиусом 2) Диаметром 3) Осевым 3. Площадь поверхности шара находится по формуле… 1) 4R2 2) R2 3) R3 4. Чему равна площадь большого круга шара, если его радиус 7 см… 49 144 14 5. Чему равен радиус шара, если его объем равен 36 см3? 6. Площадь сечения шара плоскостью равна 36 см2. Найдите диаметр шара, если плоскость находится на расстоянии 8 см от центра шара. 7. Радиус шара 10 см. Две параллельные плоскости расположены по разные стороны от центра шара. Вычислите расстояние между плоскостями, если площади сечений шара данными плоскостями равны 36 см2 и 64 см2. 8. Сечение шара плоскостью, находящейся от его центра на расстоянии 12 см, имеет площадь 25 см2. Вычислите площадь большей из частей сферы, на которые плоскость разбивает поверхность шара. 9. Точки А, В и С расположены на поверхности шара с центром в точке О так, что радиусы ОА, ОВ и ОС перпендикулярны друг другу. Вычислите объем шара, если объем пирамиды ОАВС равен 36 см3. 10. В шар радиуса 5 см вписана правильная четырехугольная пирамида. Определить объем этой пирамиды, если радиус окружности, описанной около ее основания, равен 3 см. Вариант 5 1. Используя рисунок, укажите высоту шарового сектора… 1) ОС 2) ОА 3) СА 2. Часть шаровой поверхности, принадлежащая шаровому слою, называется… 1) Шаровым сектором 2) Шаровым поясом 3) Шаровым сегментом 3. Площадь круга вычисляется по формуле… 1) 2R2 2) R2 3) 4R2 4. Чему равен диаметр шара, если площадь его поверхности равна 16 см2… 1) 16; 2) 8; 3) 4; 5. Чему равен объем шарового сегмента, если его высота 6 см, а радиус – 8 см? 6. Найдите объем шара, если площадь сечения шара плоскостью находящейся на расстоянии 9 см от центра равна 144 см2. 7. Радиус шара 13 см. Площади сечений шара параллельными плоскостями равны 144 см2 и 69 cм2. Вычислите расстояние между плоскостями, если пересекают один радиус. 8. Около шара описан прямой параллелепипед, у которого диагонали основания равны 3 см и 4 см. Определить полную поверхность параллелепипеда. 9. Правильная треугольная призма, объем которой 432 3 см3 вписана в шар. Вычислите радиус шара, если площадь основания призмы равна 27 3 см2. 10. В конус, образующая которого наклонена к основанию под углом 60 о, вписан шар. Радиус окружности касания сферической и конической поверхностей равен 4 см. Найти длину образующей конуса. Вариант 6 1. Используя рисунок, укажите радиус большого круга… 1) СТ 2) ОМ 3) ОС 2. Шаром называется тело, состоящее из всех точек пространства, находящихся от данной точки на расстоянии… 1) Равным заданному 2) Меньше заданного 3) Не превосходящем заданного 3. Площадь сферического сегмента находится по формуле… 1) 2R2H 2) 2RH 3) RH 4. Чему равен радиус шара, если площадь его поверхности равна 100 см2… 1) 10; 2) 5; 3) 4; 5. Чему равен объем шарового сектора, если его радиус 3 см, а высота – 2 см? 6. Площадь сечения шара плоскостью равна 36 см2. Найдите радиус шара, если плоскость находится на расстоянии 8 см от центра шара. 7. Площадь сечения шара некоторой плоскостью равна 4 см2, а расстояние от центра шара до этой плоскости равно 4 см. Вычислите площадь сферы, которая служит границей данного шара. 8. В шаре проведены два взаимно перпендикулярных сечения на расстоянии 8 см и 12 см от центра. Вычислите радиус шара, если длина общей хорды сечений равна 18 см. 9. Объем прямой призмы равен 18(2+ 3 ) см3. В основании призмы лежит равнобедренный треугольник АВС (АС=ВС) с углом 30о при вершине С. Найдите радиус описанного вокруг призмы шара, если длина бокового ребра призмы равна 8 см. 10. В шар вписан конус. Площадь осевого сечения конуса 9 см 2, а угол между высотой и образующей равен 45о. Найти объем шара. Вариант 7 1. Используя рисунок, укажите высоту шарового пояса … 1) ОА 2) СА 3) ОС 2. Шаровым слоем называется часть шара, расположенная между двумя… 1) Параллельными плоскостями, пересекающими шар 2) Перпендикулярными плоскостями, пересекающими шар 3) Любыми плоскостями, пересекающими шар 3. Площадь сферы вычисляется по формуле… 1) R2 2) R3 3) 4R2 4. Чему равен радиус шара, если его объем равен 36 см3… 1) 3; 2) 6; 3) 9; 5. Диаметр шара равен 8 см. Чему равна площадь его поверхности? 6. Найдите радиус сечения шара плоскостью, находящейся на расстоянии 8 см от центра шара, если радиус шара 10 см. 7. Через точку С, делящую радиус ОА шара пополам, проведена секущая плоскость, перпендикулярная этому радиусу. Вычислите площадь сферы, которая служит границей данного шара, если площадь сечения шара равна 12 см2 8. Площадь сечения шара плоскостью равна 15 см2. Расстояние от секущей плоскости до центра равно 30 см. Найти площадь поверхности шара. 9. Вычислите объем шара, описанного около пирамиды SABCD, основание которой – квадрат со стороной 4 2 см, а ее боковое ребро SB перпендикулярно плоскости основания и имеет длину 6 см. 10. В конус помещен шар так, что их поверхности касаются. Радиус шара равен 6 см, а угол при вершине осевого сечения конуса равен 60о. Найти объем тела, ограниченного поверхностями шара и конуса. Вариант 8 1. Используя рисунок, укажите радиус диаметральной плоскости шара… 1) СТ 2) ОС 3) ОМ 2. Шаровым сектором называется тело, состоящее из… 1) Шарового сегмента и конуса с вершиной центре шара, имеющих общее основание 2) Шарового сегмента и конуса, имеющих общее основание 3) Шарового сектора и конуса с вершиной центре шара, имеющих общее основание 3. Длина окружности находится по формуле… 1) R2 2) 4R 3) 2R 4. Чему равен диаметр шара, если его объем равен 288 см3… 1) 12; 2) 24; 3) 6; 5. Радиус шара равен 7 см. Чему равна площадь его поверхности? 6. Найдите площадь поверхности шара, если площадь сечения шара плоскостью находящейся на расстоянии 3 см от центра равна 16 см2. 7. Радиус шара равен 3 см. Точка А, лежащая на плоскости касательной к шару, удалена от точки касания на 3 3 см. Вычислите расстояние от точки касания до точки пересечения шара с прямой, проходящей через центр шара и точку А. 8. Площадь сечения шара плоскостью равна 16 см2. Найти расстояние от плоскости сечения до центра шара, если объем шара равен 500/3 см3. 9. Определить объем шарового сектора, если радиус окружности его основания равен 9 см, а сегментная поверхность равна 90 см2. 10. Высота конуса является диаметром шара, который пересекает конус по некоторой окружности. Найдите радиус окружности, если образующая конуса равна 8 см, а угол при вершине осевого сечения равен 60о. Вариант 9 1. Используя рисунок, укажите точки поверхности шара … 1) А 2) О 3) М 2. Плоскость, проходящая через точку шаровой поверхности и перпендикулярная радиусу, проведенному в эту точку, называется… 1) Секущей 2) Касательной 3) Диаметральной 3. Площадь сектора в n градусов вычисляется по формуле… 1) R2n/180 2) R2n/360 3) R2/360 4. Чему равен объем шара, если его радиус равен 6 см… 1) 36 2) 144 3) 288 5. Чему равен диаметр шара, если площадь его поверхности равна 16 см2? 6. Площадь поверхности шара равна 81 см2. Чему равен объем шара? 7. Сечение шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144 см2 и 25 cм2. Вычислите радиус шара, если расстояние между параллельными плоскостями равно 17 см. 8. Площадь сечения шара плоскостью в 8 раз меньше площади поверхности шара. Найти расстояние от плоскости сечения до центра шара, если радиус шара равен 242 см. 9. В шар радиуса 4 см вписана правильная шестиугольная усеченная пирамиды, у которой плоскость нижнего основания проходит через центр шара, а боковое ребро составляет с плоскостью основания угол 60о. Определить объем пирамиды. 10. Центр шара совпадает с центром основания конуса, а го радиус равен радиусу конуса. Найдите радиус окружности, по которой шар пересекает поверхность конуса, если высота конуса 12 см, а угол при вершине осевого сечения равен 60о. Вариант 10 1. Используя рисунок, укажите центр шара… 1) С 2) А 3) О 2. Плоскость, проходящая через центр шара, называется… 1) Секущая 2) Касательная 3) Диаметральная 3. Площадь поверхности шарового пояса вычисляется по формуле… 1) 2RH 2) RH 3) 2R 4. Чему равен объем шара, если его диаметр равен 6 см… 1) 12 2) 36 3) 36 5. Чему равен радиус шара, если площадь его поверхности равна 100 см2? 6. Найдите объем шара, если длина окружности сечения шара плоскостью находящейся на расстоянии 9 см от центра равна 24 см. 7. Объем шара равен 12 cм3. Найти объем другого шара, у которого площадь поверхности в 9 раз больше, чем у данного шара. 8. Радиус круга, полученного при сечении шара плоскостью, вдвое меньше радиуса шара. Найти объем шара, если площадь сечения равна 93 см2. 4 9. Через конец радиуса шара под углом 60о проведена плоскость. Найти объем шара, если площадь полученного сечения равна 3 36 см2. 10. Радиусы основания цилиндра и большого круга шара равны. Полная поверхность цилиндра относится к поверхности шара как 5:2. Найти отношение их объемов. Ответы Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10 1 3 1 2 1 2 2 3 3 1 3 2 3 3 2 2 2 3 1 1 2 3 3 3 2 2 1 2 2 3 3 2 1 4 3 2 3 1 3 2 1 1 3 3 5 36 288 12 3 216 12 64 196 4 5 6 5 10 36 20 4500 10 6 25 7 12 144 576 14 5 80 64 3 13 324 8 100 441 6 650 36 17 180 3 11 36 9 4 3 17 288 10 5 288 450 84 64 10 3 3384 2 54 16 36 36 3 6 3 972 4500


