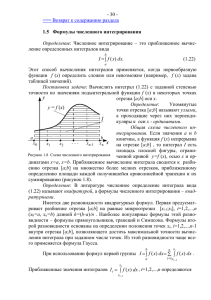
Формула трапеций и ее остаточный член.
advertisement
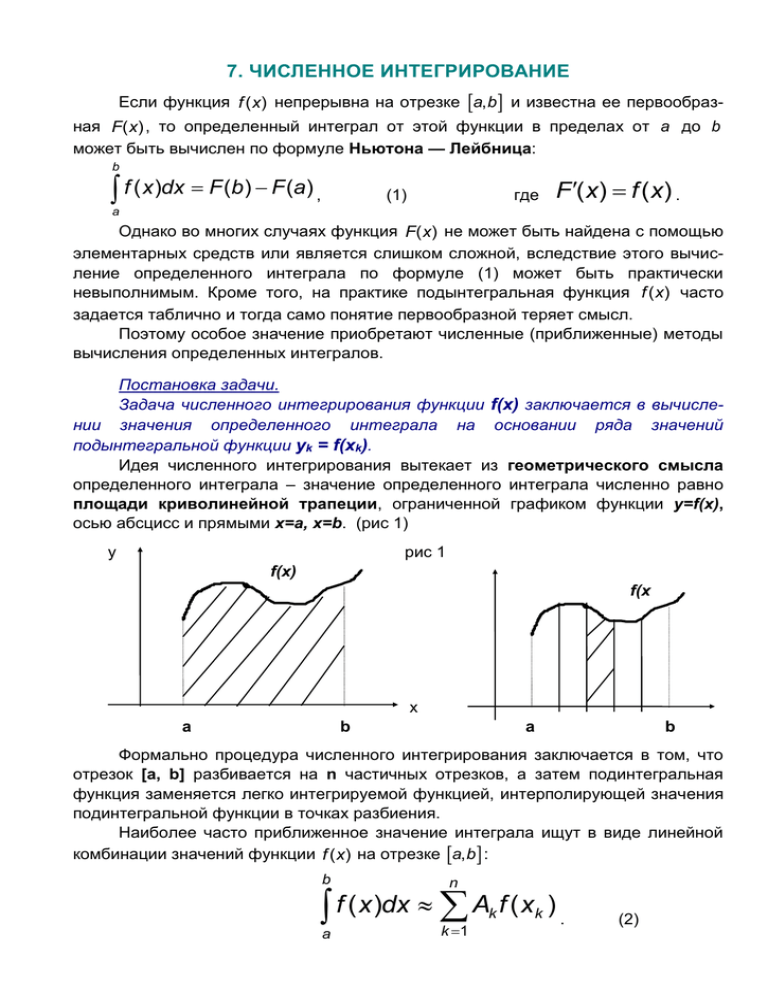
7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ Если функция f ( x) непрерывна на отрезке a, b и известна ее первообразная F( x) , то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона — Лейбница: b f ( x )dx F (b) F (a) , где (1) F( x) f ( x) . a Однако во многих случаях функция F( x) не может быть найдена с помощью элементарных средств или является слишком сложной, вследствие этого вычисление определенного интеграла по формуле (1) может быть практически невыполнимым. Кроме того, на практике подынтегральная функция f ( x) часто задается таблично и тогда само понятие первообразной теряет смысл. Поэтому особое значение приобретают численные (приближенные) методы вычисления определенных интегралов. Постановка задачи. Задача численного интегрирования функции f(x) заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции yk = f(xk). Идея численного интегрирования вытекает из геометрического смысла определенного интеграла – значение определенного интеграла численно равно площади криволинейной трапеции, ограниченной графиком функции y=f(x), осью абсцисс и прямыми х=а, х=b. (рис 1) рис 1 y f(x) f(x x a b a b Формально процедура численного интегрирования заключается в том, что отрезок [а, b] разбивается на n частичных отрезков, а затем подинтегральная функция заменяется легко интегрируемой функцией, интерполирующей значения подинтегральной функции в точках разбиения. Наиболее часто приближенное значение интеграла ищут в виде линейной комбинации значений функции f ( x) на отрезке a, b : b n f ( x )dx A f ( x k a k 1 k ) . (2) Приближенное равенство (2) называют квадратурной формулой, определяемой узлами xk и коэффициентами Ak . Выражение а разность в правой части b n a k 1 (2) Rn (f ) f ( x )dx Ak f ( xk ) называют квадратурной суммой, остаточным членом, или остатком, квадратурной формулы. Рассмотрим общие вид квадратурных формул. 7.4. Квадратурные формулы Ньютона — Котеса b Пусть для данной функции y f ( x) требуется вычислить интеграл ydx . a ba , разобьем отрезок a, b с помощью равноотстоящих точек n x0 a , xi x0 ih , i 1, n 1, xn b на n равных частей, и пусть y i f ( xi ) , i 0, n . Выбрав шаг h Заменяя функцию y интерполяционным полиномом Лагранжа Ln ( x ) , получим приближенную квадратурную формулу: где Ai xn n x0 i 0 ydx A y i i , (3) — некоторые постоянные коэффициенты. Выведем явные выражения для коэффициентов Ai . Для этого вспомним некоторые формулы из предыдущих лекций. x x0 Введя переменную q , полином Лагранжа можно переписать в виде: h ( 1)n i y i q(q 1) (q n) Ln ( x ) i !( n i )! q i i 0 n (4) Заменяя в (3) функцию полиномом Лагранжа в виде (4), учитывая сделан- ( 1)n i q(q 1) (q n) dx , ные выше выкладки, имеем: Ai i !( n i )! q i x0 xn или, переходя к новой переменной q x x0 1 , dq dx и заменяя пределы h h интегрирования, получим выражение: ( 1)n i q(q 1) (q n) Ai h dx , i 0, n . i !(n i )! 0 q i n Ai (b a)Hi , Так как h ba , то обычно полагают n Где 1 ( 1)n i q(q 1) (q n) Hi dq , n i !(n i )! 0 q i n i 0, n , (5) постоянные, называемые коэффициентами Ньютона — Котеса. Квадратурная формула (3) при этом принимает вид: b n a i 0 ydx (b a) H y , i (6) i ba , y i f (a ih) , i 0, n . n Квадратурные формулы Ньютона — Котеса (6) дают на одном участке интегрирования различные представления для различного числа n . где h Формула трапеций и ее остаточный член. 1 q(q 1) 1 1 dq , H1 q dq , Из формулы (5) при n 1 имеем: H0 q 2 2 0 0 1 x1 Отсюда h ydx 2 (y 0 y1 ) . Мы получили известную формулу трапеций. x0 Остаточный член квадратурной формулы (3) равен R x1 h ydx ( y 0 y1 ) . 2 x0 Предполагая, что y C 2 a, b , выведем простую формулу для остаточного члена. Будем рассматривать R R(h) как функцию шага h , тогда можно положить: R (h ) x0 h x0 ydx h y ( x0 ) y ( x0 h) . 2 Дифференцируя эту формулу по h последовательно два раза, получим: 1 h 1 h R (h) y ( x0 h) y ( x0 ) y ( x0 h) y ( x0 h) y ( x0 h) y ( x0 ) y ( x0 h) 2 2 2 2 1 1 h h R (h) y ( x0 h) y ( x0 h) y ( x0 h) y ( x0 h) , и 2 2 2 2 причем R(0) 0 и R(0) 0 . Интегрируя по h и используя теорему о среднем, последовательно выводим: h h 1 1 R (h) R (0) R (t )dt ty ( x0 t )dt y (1) , где 1 x0 , x0 h , и 2 2 0 0 h h h 1 2 1 h3 2 R(h) R(0) R (t )dt t y (1)dt y () t dt y () , 40 4 12 0 0 где 1 x0 , x0 h . Таким образом, окончательно имеем: где 1 x0 , x0 h . h3 R y () , 12 (7) Отсюда, в частности следует, если y 0 , то формула трапеций дает значение интеграла с избытком, если же y 0 — то с недостатком. b Для вычисления интеграла ydx разделим отрезок интегрирования на n a равных частей x0 , x1 , x1, x2 , …, xn 1, xn и к каждому применим формулу трапеba и обозначая через y i f ( xi ) , n подынтегральной функции в точках xi , будем иметь: ций. Полагая h b h ydx 2 ( y 0 y1 ) a b h ( y1 y 2 ) 2 y0 ydx h( 2 или y1 y 2 i 0, n , значения h ( y n 1 y n ) 2 y n 1 a yn ). 2 (8) Геометрически формула (8) получается в результате замены кривой y f ( x) ломаной линией. Если y C 2 [a, b ] , то остаточный член квадратурной формулы (8) в силу (7) n xi h n h h3 n R ydx ( y i 1 y i ) ydx ( y i 1 y i ) y (i ) , 2 i 1 2 12 i 1 i 1 x0 xi 1 xn равен: (9) где i xi 1, xi . 1 n (10) y i . n i 1 Известно, что заключается между наименьшим m и наибольшим M значе Рассмотрим среднее арифметическое: ниями второй производной y на отрезке a, b , т. е. m M . Так как y интегрирована на отрезке a, b , то в качестве своих значений на a, b она принимает все промежуточные числа между m и M. Следовательно, найдется точка a, b такая, что y . b a h y nh 3 R y , 12 12 2 Из формул (9) и (10) имеем: где a, b . (11) Формула Симпсона и ее остаточный член. 1 1 q q 1 q 2 1 H0 dq , 2 20 q 6 2 Из формулы (5) при n 2 получаем: 1 1 q q 1 q 2 2 H1 dq , 2 10 q 1 3 2 x2 Так как x2 x0 2h , имеем: 1 1 q q 1 q 2 1 H2 dq . 2 20 q2 6 2 h ydx 3 ( y 0 4 y1 y 2 ) . x0 Полученная формула носит название формулы Симпсона. Геометрически эта формула получается в результате замены данной кри- вой y f x параболой y L2 x , проходящей через три точки M0 x0 , y 0 , M1 x1, y1 и M2 x2 , y 2 (рис.). Остаточный член формулы Симпсона равен: R x2 h ydx 3 ( y 0 4 y1 y 2 ) . x0 Предполагая, что y C a, b , аналогично тому, как это делалось для форn мулы трапеций, выведя более простое выражение для R . Фиксируя среднюю точку xi и рассматривая R R h как функцию шага h h 0 , будем иметь: R x1 h x1 h ydx h y x1 h 4y x1 y x1 h . 3 Дифференцируя функцию R h по h последовательно три раза, получим: 1 h R h y x1 h y x1 h y x1 h 4h( x1 ) y x1 h y x1 h y x1 h 3 3 2 4 h y x1 h y x1 h y x1 y x1 h y x1 h , 3 3 3 2 1 h R h y x1 h y x1 h y x1 h y x1 h y x1 h y x1 h 3 3 3 1 h y x1 h y x1 h y x1 h y x1 h , 3 3 1 1 h R h y x1 h y x1 h y x1 h y x1 h y x1 h y x1 h 3 3 3 h 2 y x1 h y x1 h h 2 y IV , 3 3 где x1 h, x1 h . Кроме того, очевидно, что R 0 0 , R 0 0 , R 0 0 . Последовательно интегрируя R h и используя теорему о среднем, находим: h h h 2 2 2 R h R 0 R t dt t 2 y IV dt y IV t 2dt h 3 y IV , 30 3 9 0 0 где x1 h, x1 h . h h h 2 2 2 R h R 0 R t dt t 3 y IV dt y IV t 3dt h 4 y IV , 90 9 18 0 0 где x1 h, x1 h . h h h 1 1 1 5 IV R h R 0 R t dt t 4 y IV dt y IV t 4dt h y , 18 0 18 90 0 0 где x1 h, x1 h . Таким образом, остаточный член формулы Симпсона равен: h5 IV R y , 90 x0 , x2 . Очевидно, что формула Симпсона является точной для полиномов не только второй, но и третьей степени. Пусть n 2m есть четное число и y i f xi , i 0, n — значения функции ba ba . n 2m Применяя формулу Симпсона к каждому удвоенному промежутку x0, x2 , x2, x4 , ..., x2m2, x2m длины 2h будем иметь: y f x для равноотстоящих точек a x0 , x1, ..., xn b с шагом h b h ydx 3 y 0 4 y1 y 2 a h h y 2 4y 3 y 4 ... y 2m 2 4y 2m 1 y 2m . 3 3 Отсюда получаем общую формулу Симпсона b ydx a h y 0 y 2m 4 y1 y 3 ... y 2m 1 2 y 2 y 4 ... y 2m 2 . 3 Если y C 4 a,b , то ошибка формулы Симпсона на каждом промежутке h5 IV y k , k x2k 2 , x2k . 90 Суммируя все эти ошибки, получим остаточный член общей формулы h 5 m IV R Симпсона в виде: y k . 90 k 1 x2k 2, x2k , k 1, m , дается формулой: rk Так как y IV x непрерывна на a, b , то найдется точка a, b такая, что 1 m IV y y k , a, b . m k 1 IV b a h y IV mh5 IV R y , 90 180 5 Поэтому будем иметь: где a, b . (12) Об оценке точности квадратурных формул Как следует из оценочных формул (11) и (12) оценка погрешности метода интегрирования по формулам трапеций и Симпсона возможна лишь тогда, когда подынтегральная функция задана аналитически. Однако, даже в этом случае на практике широко применяется следующий прием, пригодный для каждого из рассмотренных методов интегрирования. Искомый интеграл вычисляется дважды: при делении отрезка a, b на n частей и 2n частей (разумеется, при интегрировании по формуле Симпсона n к тому же должно быть четным). Вслед за этим полученные значения интеграла I n и I2n сравниваются, и совпадающие первые десятичные знаки считаются верными. Для оценки погрешности метода Симпсона может использоваться простая формула. Пусть R n и R2n — погрешность интегрирования по методу Симпсона, соответственно при Учитывая (12), получим: n и 2n отрезках интегрирования. Rn h4 4n , где h n и h 2n — шаги интегрирования. Тогда R n =16R 2n R2n h2n Если I — истинное значение интеграла (1), то I = I n +R n или I = I 2n +R 2n . R 2n = I2n In . 15 Эта формула удобна для практической оценки погрешности метода Симпсона. Из оценки остаточного члена следует, что ошибка по методу трапеций и методу Симпсона уменьшается с уменьшением шага интегрирования. Однако, это чисто теоретическое утверждение. Дело в том, что в процессе вычислений при последовательном удвоении числа отрезков разбиения растут ошибки округления, значение которых с некоторого момента ставит предел достижимой точности результата интегрирования. Исследуем формулы с равноотстоящими узлами. К их числу относятся формулы трапеций, Симпсона, Ньютона — Котеса. Точность квадратурной формулы в основном характеm ризуется порядком остаточного члена R = O(h ), где h= b a — шаг и m — натуральн. число. n Из этого следует, что Квадратурная формула считается тем точнее, чем больше число m; в этом смысле формула Симпсона является более точной, чем формула трапеций. Можно показать, что в конкретных случаях более грубая квадратурная формула при одном и том же h может дать лучший результат, чем более точная. 2 Например, для f(x) = –8 + 45x – 25x 4 имеем: 1 I f ( x )dx ( 8 x 15 x 3 5 x 5 ) 1 1 4. 1 При h = 1 формула трапеций дает точное решение: I1 1 1 f ( 1) f (0) f ( 1) 4 , 2 2 тогда как формула Симпсона при h = 1 не обеспечивает даже знака интеграла: I2 1 8 (f ( 1) 4f (0) f ( 1)) . 3 3 Точность квадратурной формулы при фиксированном числе узлов существенно зависит от расположения этих узлов. При неудачном расположении узлов квадратурная формула может дать сильно искаженные результаты. При наличии значительного числа нулей подынтегральной функции или при большом числе ее экстремумов (т. е. когда много нулей производной f ( x) ) точность квадратурных формул сильно понижается. Поэтому шаг h следует выбирать так, чтобы он был намного меньше расстояний между соседними нулями функции f(x) и ее производной f ( x) . Для этого рекомендуется, например, основной отрезок интегрирования [a,b] разбить на частичные отрезки [α,β], внутри каждого из которых, функции f(x) и f ( x) сохраняют постоянный знак (если это возможно!), и производить вычисление интеграла по частям, выбирая для каждого отрезка, вообще говоря, свой шаг.