Ярославль 2015

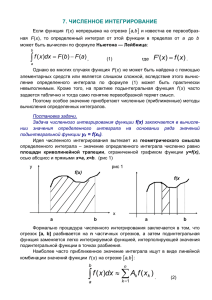
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ
ЯРОСЛАВСКОЙ ОБЛАСТИ
Государственное профессиональное образовательное учреждение
Ярославской области
"ЯРОСЛАВСКИЙ АВТОМЕХАНИЧЕСКИЙ КОЛЛЕДЖ"
МЕТОДИЧЕСКОЕ ПОСОБИЕ
ПО ВЫПОЛНЕНИЮ ВНЕАУДИТОРНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
по дисциплине
ЕН. 01
ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
основной профессиональной образовательной программы (ОПОП)
по специальностям СПО
09.02.03 Программирование в компьютерных системах
09.02.01 Компьютерные системы и комплексы
базовой подготовки
Ярославль
2015
ОДОБРЕНО И
Составлены в соответствии с
РЕКОМЕНДОВАНО
Государственными требованиями к
предметно-цикловой комиссией
минимуму содержания и уровню
подготовки выпускников по
математики, естествознания и
специальностям
естественно-научных дисциплин
09.02.03 Программирование в
компьютерных системах, 09.02.01
Компьютерные системы и комплексы
по программе базовой подготовки
Разработчик:
Бокарева С.В., преподаватель ГПОУ ЯО
"Ярославский автомеханический
колледж"
150054, г. Ярославль, ул.Автозаводская, 1-а,
Тел/факс (4852) 73-26-43; E-mail: avtomeh@bk.ru
Методическое пособие составлено в соответствии с рабочей программой
учебной дисциплины ЕН. 01
ЭЛЕМЕНТЫ
ВЫСШЕЙ МАТЕМАТИКИ на
основе Федерального государственного образовательного стандарта основной
профессиональной образовательной программы (ОПОП)
по специальностям СПО
системах , 09.02.01
09.02.03
Программирование в компьютерных
Компьютерные системы и комплексы базовой
подготовки.
Пособие содержит краткий справочный материал, образец выполнения
задания и варианты заданий. Методические указания предназначены студентам
для выполнения внеаудиторной самостоятельной работы.
Пособие разработано с целью:
- закрепления полученных теоретических знаний;
- ликвидации пробелов знаний обучающихся по данной теме;
- формирования самостоятельности при работе с заданиями с применением
методических рекомендаций.
Содержание внеаудиторной самостоятельной работы направлено на усвоение
знаний и умений , формирование общих и профессиональных компетенций,
предусмотренных ФГОС СПО по специальностям 09.02.03
Программирование в компьютерных системах, 09.02.01 Компьютерные
системы и комплексы.
Данные методическое
пособие
может
использоваться также для
выполнения внеаудиторной самостоятельной работы по дисциплине ЕН. 01
МАТЕМАТИКА для всех технических специальностей
Предисловие
Одним из видов внеаудиторной самостоятельной работы
домашняя контрольная работа по отдельной теме
темам. Данными
воспользоваться,
методическими
указаниями
является
или по нескольким
студенты
могут
если испытывают затруднения при выполнении заданий
практической работы или домашней контрольной работы после изучения
учебного материала на занятиях. Предполагается, что часть теоретического
материала
учащиеся
литературе. Домашнюю
повторяют
контрольную
по конспектам или
работу
учащиеся
рекомендуемой
выполняют по
индивидуальным вариантам в отдельной тетради с последующей защитой.
Внеаудиторная самостоятельная работа
Тема: Численное интегрирование ( приближенные методы вычисления
определенного интеграла : метод прямоугольников, метод трапеций)
Цель работы: научиться вычислять определенные интегралы приближенными
методами( методом прямоугольников, методом трапеций) и вычислять
погрешность.
Перед началом работы необходимо знать: что называется определенным
интегралом, формулу Ньютона-Лейбница, метод подстановки, формулы метода
прямоугольников и метода трапеций.
После окончания работы необходимо уметь: вычислять определенные
интегралы приближенными методами( методом прямоугольников, методом
трапеций) и погрешность.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Повторить материал данной темы по конспекту или по одному из
учебников:
Дадаян А. А. , Математика, М., Форум-Инфра-М, 2011 ( §10.14 ) ;
Омельченко В.П., Курбатова Э.В. Математика: Учебное пособие. Ростов
н/д: Феникс, (§ 3.1 )
2. Ознакомиться с теорией ( основные формулы).
3. Изучить образец выполнения задания.
4. Решить задачу своего варианта.
5. Оформить отчет и защитить его.
Приближенное вычисление определенного интеграла
Пусть требуется найти определенный интеграл
, причем
функция
считается непрерывной на отрезке
. Если от
подынтегральной функции
первообразная
находится легко, то
значение рассматриваемого интеграла находится по формуле НьютонаЛейбница:
Но не в каждом случае отыскание первообразной для подынтегральной функции
является достаточно простым, а также не для всякой непрерывной функции
существует первообразная, выражающаяся через элементарные функции. В
подобных случаях применяют приближенные формулы, которые позволяют
вычислить определенный интеграл с любой степенью точности.
Наиболее часто используются три формулы приближенного вычисления
определенного интеграла – формула прямоугольников, формула трапеций и
формулу парабол или формула Симпсона, основанные на геометрическом
смысле определенного интеграла: если функция
непрерывна и
положительна
интеграл
на
отрезке
,
то
определенный
представляет собой площадь криволинейной трапеции,
ограниченной линиями
1. Формула прямоугольников
Пусть на отрезке
численно определенный
криволинейной трапеции.
задана непрерывная функция
интеграл
Разобьем основание этой трапеции (отрезок
отрезков длины
,
. Вычислим
который
) на
n
равен
площади
равных частей-
Величину h будем называть шагом разбиения. В результате получим точки
Можно записать, что
В середине
каждого такого элементарного отрезка отметим
точку
. Приняв ординату этой точки за высоту, построим
прямоугольник с площадью
(рис. 2).
Тогда сумма площадей всех n прямоугольников равна площади ступенчатой
фигуры, которая представляет собой приближенное значение искомого
определенного интеграла
:
Полученная формула называется формулой прямоугольников.
Можно рассмотреть две интерпретации этого метода т. е. с недостатком и с
избытком.
1) Если суммировать площади прямоугольников, которые показывают
площадь криволинейной трапеции с недостатком [Рисунок1]
[Рисунок1]
то получим формулу:
b

a
n 1
f x   dx  h   yi , 
i 0
ba
  y0  y1  .....  y n1 
n
2) Если суммировать площади прямоугольников, которые показывают
площадь криволинейной трапеции с избытком [Рисунок2], то получим
формулу:
[Рисунок2],
b

a
n
f x   dx  h   yi , 
i 1
ba
  y1  y 2  .....  y n 
n
С увеличением n результат становится более точным.
2. Формула трапеций
Эту формулу получают аналогично формуле прямоугольников: на каждом
частичном отрезке криволинейная трапеция заменяется обычной.
Пусть необходимо вычислить определенный интеграл
. Разобьем
отрезок интегрирования
на
n
равных частей длины
. В
результате
получим
точки
.
Пусть
– соответствующие им ординаты функции. Тогда можно
записать, что
Заменим кривую
ломаной линией, звенья которой соединяют концы
ординат
и
приближенно
. Тогда площадь криволинейной трапеции
сумме
площадей
обычных
трапеций
с
равна
основаниями
b

a
и высотой
, то есть
y  yn
 y  y1 y1  y 2
f x   dx  h   0

.....  n1
2
2
 2
  y0  y n

 y1  y 2  ...  y n1 

  2

Получаем
b

a
 y  yn n 1 
f x   dx  h   0
  yi ,
i 1
 2

где
h
ba
n
ОСНОВНЫЕ ФОРМУЛЫ
1) Формула Ньютона-Лейбница
b
 f ( x)  dx  F (b)  F (a)
a
2) Формула метода прямоугольников с недостатком
b

a
n 1
f x   dx  h   yi ,
i 0
где
h
ba
n
3) Формула метода прямоугольников с избытком
b

n
f x   dx  h   yi ,
где
h
i 1
a
ba
n
4) Формула метода трапеций
b

a
 y  yn n 1 
f x   dx  h   0
  yi ,
i 1
 2

где
h
ba
n
Погрешность
E
точное значение
 приближённое значение
приближённое значение
 100%
Пример 1.
2


2
 2 x x  1  dx
3
,
n5
1
Вычислить данный интеграл методом прямоугольников ( с недостатком и с
избытком), методом трапеций и определить погрешности в каждом случае.
Решение:
1) Составим таблицу, вычислив предварительно значения каждой колонки
 
 2  1  1  1  0
 2  1,2  1,2  1  0,2044
 2  1,4  1,4  1  2,4773
 2  1,6  1,6  1  12,1485
 2  1,8  1,8  1  40,4619
 2  2  2  1  108
a  1, b  2, n  5
ba
2 1
h
, h
 0,2
n
5
x0  a  1
y i  2 xi  xi2  1
x1  x0  h , x1  1  0,2  1,2
y2
x2  x1  h , x2  1,2  0,2  1,4
y3
y0
y1
x3  x2  h , x3  1,4  0,2  1,6
x4  x3  h , x4  1,6  0,2  1,8
y4
y5
x5  x4  h , x5  1,8  0,2  2
i
Xi
Yi
0
1
0
1
1,2
0,2044
2
1,4
2,4773
3
1,6
12,1485
4
1,8
40,4619
5
2
108
3
3
2
2
3
2
3
2
3
2
3
2
3
2) Вычислим интеграл методом прямоугольников с недостатком
b

n 1
f x   dx  h   yi ,  h   y0  y1  y2  y3  y4 
i 0
a
 2 xx
2
2

 1  dx  0,2  0  0,2044  2,4773  12,1485  40,4619  0,2  55,2921  11,0584
3
1
3) Вычислим интеграл методом прямоугольников с избытком
b
n
a
i 1
 f x  dx  h   y ,  h   y
 2 xx
2
1
2

i
1
 y 2  y3  y 4  y5 
 1  dx  0,2  0,2044  2,4773  12,1485  40,4619  108  0,2  163,2921  32,6584
3
4) Вычислим интеграл методом трапеций
 y0  у5

 y1  y2  y3  y4 
2

b
 f x  dx  h  
a
 2 xx
2
1
2
3
 0  108

 1  dx  0,2  
 0,2044  2,4773  12,1485  40,46194   21,8584
 2


5) Вычислим точное значение интеграла (методом подстановки)
tв  22  1  3
t  x2 1

3
dt  x 2  1  dx t  12  1  0 3
t4
2
3 dt
3
н
2
x
x

1

dx


2
x

t


t

dt

1
0
dt  2 x  dx
2 x 0
4
dt
dx 
2x
2



3

6) Вычислим погрешности
E
E1 
E2 
E3 
точное значение
 приближённое значение
приближённое значение
20,25  11,0584
11,0584
20,25  32,6584
32,6584
20,25  21,8584
21,8584
 100%  83%
 100%  38%
 100%  0,7%
 100%
3

0
3 4 0 4 81


 20,25
4
4
4
Задание к индивидуальным вариантам
1) Составить и заполнить таблицу значений
2) Вычислить интеграл методом прямоугольников с недостатком
3) Вычислить интеграл методом прямоугольников с избытком
4) Вычислить интеграл методом трапеций
5) Вычислить точное значение интеграла (методом подстановки)
6) Вычислить погрешности
Варианты
1
3
x
1  x  dx
2
n=10
2
0
3
6 x  5  dx
n=10
4
1
5
 2x  x

3
2
 1  dx
2
n=10
6
13
 2 x  x

1
3
 2  dx
2
 2 x  x
n=10

4
 1  dx
2
n=10
 dx
n=10
3
 dx
n=10
2
 1  dx
2
 4 x  1
8
 4 x  2 x
dx
1 3x  23
4 x 3  dx
 x
4

2
10
5
2
dx
x4

0
2
0
2
 3x  1
n=10
1
1
1
n=10
2
0
11
 dx
1
0
9
2
0
0
7
 2 x  1
0
9

2
 1
2
n=10
12
2
4 x  dx
 x
1
n=10
14
1
n=10

2
2
n=10

n=10

1
2
3
 3x  x  1  dx
0
2
15
2
6 x  dx
 x
17
n=10
 1
2
2
1
 3x  x
3

2
 2  dx
18
n=10
 3x

2
2
 2 x  1  dx
20
n=10
1
21
23
22
2
dx
0 5x  13
 4 x2 x
n=10
 4 x  3
3
 x x
2

2
 3  dx
2


2
 2 x x  1  dx
3
2 x  dx
 x
2
0
8

0
31
n=10
3

n=10
2
 4  dx
1
3x 2  dx
 x
3
n=10
24
n=10

1
 2 xx
2

1
2
2
 5  dx
n=10
3
 2 x  1  dx

n=10
0
2
29
2
0
1
2
 dx
2
n=10
26
 4 x
3
1
1
27
n=10
2
1
0
25

2
3
 6 x x  1  dx
1
0
19

2
1
1
2
16
n=10
 1
2
28
3
8 x  dx
 x
dx
x 1
n=10
 1
3
2 х  dx
 3x  2
 dx
1

0
2
3
30
n=10
32
n=10
2
1
2
x2 1
n=10
1
 5x  1
2
 dx
n=10
0
Контроль выполнения письменной части работы: проверка
преподавателем
Защита работы : объяснение своих вычислений, ответы студентом на
вопросы преподавателя .
Контрольные вопросы:
1) Определение определенного интеграла
2) Формула Ньютона – Лейбница
3) Метод подстановки при вычислении определенного интеграла
4) Численные методы интегрирования
5) Формулы численных методов интегрирования
6) Формула вычисления погрешности