3, 4. Понятие временного ряда. Виды временных рядов
advertisement

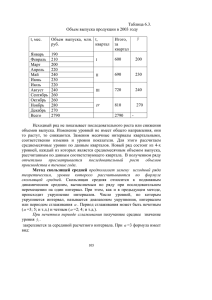
1. Понятие эконометрики. Эконометрика—один из видов научно-прикладных исследований экономических процессов и явлений, ставящих своей целью построение определенных экономико-математических моделей на базе экономической теории, экономической статистики и методов математической статистики. Основой эконометрических моделей являются регрессионные модели. Построенные на базе имеющейся статистической информации, регрессионные модели позволяют исследовать зависимости между различными экономическими факторами, описать эти зависимости в виде математических уравнений. Применить в прогнозировании. 3, 4. Понятие временного ряда. Виды временных рядов. Структура нестационарного временного ряда. Упорядоченная последовательность показателей, которые характеризуют развитие явления во времени, называется временным рядом. Временные ряды экономических показателей можно подразделить на два основных вида: стационарные и нестационарные. Стационарные временные ряды являются отражением некоторого случайного процесса, а сам процесс остаётся в равновесии относительно некоторого постоянного среднего уровня, и его характеристика не зависит от момента времени. В нестационарных временных рядах случайные колебания происходит относительно среднего уровня, который со временем изменяется под влиянием различных факторов. Общая долговременная тенденция временного ряда называется трендом. Временные ряды некоторых экономических показателей обнаруживают периодичность изменения своих уровней относительного некоторого среднего уровня. Такие изменения во временном ряду принято называть периодическими. В экономических исследованиях наиболее часто рассматривают сезонные и циклические колебания в зависимости от продолжительности периода колебаний и сущности экономического процесса. В общем виде структура временного ряда включает в себя следующие компоненты: 1. тренд 2. периодическую компоненту 3. случайную компоненту. Качественные характеристики временных рядов обуславливают выбор методов и моделей, применяемых для анализа и прогнозирования социально-экономических явлений. Так для временных рядов, не содержащих периодической компоненты, можно использовать два подхода: 1. подход, основанный на использовании средних 2. подход, основанный на использовании метода наименьших квадратов. Для прогнозирования на базе временных рядов с учетом периодических колебаний используются аддитивные и мультипликативные модели, методы гармонического анализа. Специальные методы применяются для прогнозирования на базе стационарных временных рядов. 7. Скользящая средняя и ее использование в экономическом анализе. Сущность метода скользящих средних состоит в укрупнении интервалов и определении средних для каждого укрупненного интервала. При этом применяют способ переменной или скользящей средней, при котором интервал y1 y 2 ... y N усреднения сдвигают каждый раз на один шаг от начала ряда. y N1 N y 2 y3 ... y N 1 y N2 N В результате укрупнения интервалов колебания абсолютных значений уровней временного ряда, скрывающие общую закономерность, взаимопогашаются в средней величине уровня данного ряда и закономерность развития изучаемого явления выступает более четко. Сглаживание временного ряда осуществляется следующим образом. Выбирается интервал сглаживания. Выбор интервала сглаживания определяется особенностью изучаемого явления и поставленной задачей исследования. Если изучаемое явление, описываемое данным временным рядом, подвержено периодическим колебаниям, то интервал сглаживания выбирается равным длине периода. Когда нет явных периодических колебаний то интервал сглаживания выбирается в зависимости от целей анализа. При этом необходимо учитывать, что, чем длиннее интервал сглаживания, тем более сглаженной будет кривая. При выборе интервала сглаживания необходимо также иметь в виду, что обычно вычисленное среднее относиться к середине интервала сглаживания, определяется как m N 1 , где N—интервал сглаживания. При N четном среднее 2 относиться к серединам промежутков между двумя уровнями эмпирического ряда, что затрудняет сопоставление фактических уровней с их «сглаженными» значениями, в данном случае для сопоставления прибегают к центрированию сглаженного ряда. Если же интервал сглаживания—число нечетное, то прибегать к центрированию нет необходимости. Сравнение фактических и сглаженных значений временного ряда. Для сравнения фактических и выровненных значений временного ряда необходимо решить вопрос об отнесении скользящей средней относительно границы интервала сглаживания. В экономических исследованиях этот вопрос может быть решен по разному в зависимости от задач анализа. Во многих задачах значение скользящей средней относят на середину интервала сглаживания. В этом случае сглаженный ряд сокращается по сравнению с с фактическим рядом с обеих сторон. Значение скользящей средней может быть отнесено на конец интервала или даже вынесено вперед на несколько шагов. Скользящие средние в таких случаях используются для прогнозных целей в основном не столько для определения точного значения прогнозируемой величины, сколько для установления направления тренда.. Центрированные скользящие средние сглаживают ряд динамики и дают более четкое представление о характере тенденции развития данного явления и на основе этого позволяют выбрать адекватную аналитическую модель тренда. 8. прогнозирование на основе метода среднего абсолютного отклонения. Временной ряд x(t) показателя Х, измеренного в прошлом на интервале t=1,…,T, аппроксимируется функцией F(t), которая строиться по правилам: F(t)=x(t-1)+A(t-1), t=3,…,T+1, A(t)=C(t)/(t-1), C(t)=C(t-1)+x(t)-x(t-1), C(1)=0/ Прогнозное значение показателя Х в году Т+1 есть F(T+1). Таким образом, метод среднего абсолютного отклонения предназначен для прогнозирования на один год. Аппроксимирующая функция вычисляется как фиксированная функция без параметров, поэтому здесь не возникает задача о наилучшей функции. По построенной функции и динамическому ряду можно вычислить среднюю абсолютную погрешность, среднюю относительную погрешность и среднеквадратическое отклонение, которые характеризуют точность аппроксимации: T T АП F (t ) x(t ) t 3 T 2 , ОП t 3 F (t ) x(t ) x(t ) T 2 ,S T t 3 F (t ) x(t )2 T 2 . 9. Прогнозирование на основе метода экспоненциального сглаживания. Прогноз вычисляется как среднее взвешенное значение всех членов ряда. Последний член «взвешивается» с множителем из интервала (0,1), предпоследний—множителем (1- ) , третий с конца—множителем 1- )(1 ) и так далее, второй—множителем (1- )Т-2 , первый—множителем (1- )Т-1. здесь Т—количество членов ряда. Сумма всех весовых коэффициентов равна единице независимо от длины ряда. Правила экспоненциального сглаживания записываются формулой: S(t)= x(t-1)+(1- )S(t-1), t=3,…,T+1, S(2)=x(1). Параметр подбирается таким образом, чтобы абсолютная или квадратичная ошибка была минимальной. Прогнозное значение Х в году Т+1 естьS(T+1). 10.Общая характеристика методов анализа и прогнозирования на основе временных рядов с периодической компонентой. Для анализа временных рядов с периодической компонентой (циклической или сезонной) в экономических исследованиях применяют ряд методов. Довольно широкое распространение получили в анализе нестационарных временных рядов с периодической компонентой модели с аддитивной и модели с мультипликативной компонентой. В этих моделях временной ряд разлагается на три компоненты: тренд—Т, сезонную компоненту S и случайную компоненту или погрешность—Е. в аддитивных моделях уровни временного ряда представлены как сумма этих компонент—Y=T+S+E, а в мультипликативных как произведение этих компонент—Y+T*S*E. Модели с аддитивной компонентой применяются в тех случаях, когда характер периодических колебаний относительно тренда примерно одинаков в течении анализируемого периода времени. Если же амплитуда колебаний относительно тренда изменяется с течением времени (увеличивается или уменьшается), то в этих случаях следует отдать предпочтение модели с мультипликативной компонентой. 11. Прогноз на основе аддитивной модели. Этап 1. Анализ данных. Построение графика на основе исходных данных. Визуальный анализ данных на основе графика, вывод о возможности использовать аддитивную модель. Этап 2. Расчет сезонной компоненты. 2.1. Расчет скользящей средней с шагом 4. 2.2. Центрирование скользящей средней. 2.3. Определение сезонной компоненты путем вычитания из уровней ряда значений центрированной скользящей средней за соответствующий момент времени. 2.4. расчет средних значений сезонной компоненты по кварталам. 2.5. корректировка средних значений сезонной компоненты. Этап 3. определение тренда. 3.1. Десезонолизация данных. На этом шаге от всех уровней ряда вычитают соответствующее значение скорректированной сезонной компоненты, получают значения содержащие тренд и случайную компоненту: YS=T+E. 3.2. построение модели тренда методом наименьших квадратов на основе десезонализированных данных. Этап 4. Определение качества модели и расчет ошибок.. Этап 5. Построение прогноза с учетом сезонных колебаний. 5.1. расчет прогнозных значений на основе модели тренда. 5.2. корректировка прогноза на сезонную компоненту. 12. прогноз на основе мультипликативной модели. Этап 1. Анализ данных. 1.1 Построение графика на основе исходных данных. 1.2. Визуальный анализ данных на основе графика, вывод о возможности использовать мультипликативную модель. Этап 2. Расчет сезонной компоненты. 2.1. Расчет скользящей средней с шагом 4. 2.2. Центрирование скользящей средней. 2.3. Определение сезонной компоненты путем деления уровней ряда на значение центрированной скользящей средней за соответствующий момент времени. 2.4. расчет средних значений сезонной компоненты по кварталам. 2.5. корректировка средних значений сезонной компоненты. Этап 3. определение тренда. 3.1. Десезонолизация данных путем деления фактических значений уровня ряда на скорректированные коэффициенты сезонности за соответствующий квартал: У/Ускор=Т*Е. 3.2. построение модели тренда методом наименьших квадратов на основе десезонализированных данных. Этап 4. Определение качества модели и расчет ошибок.. Этап 5. Построение прогноза с учетом сезонных колебаний. 5.1. расчет прогнозных значений на основе модели тренда. 5.2. корректировка прогноза на сезонную компоненту. 14,15. Задачи корреляционного анализа. Исследование парной корреляции. Корреляционный анализ используется для анализа взаимосвязи двух или более показателей. Корреляционный анализ—это метод математической статистики, который исследует взаимосвязи между показателями в целом на основе анализа выборки из этих показателей. Этапы: 1. Сбор данных. Данные для корреляционного анализа должны представлять случайную выборку из двухмерной или многомерной случайной величины. 2. Анализ данных. Проводиться для того, чтобы принять гипотезу о виде корреляционной зависимости. Проводиться путем построения графика синхронности и графика корреляционного поля. 3. Вычисление коэффициента корреляции. 4. проверка статистической значимости выборочного показателя корреляционной зависимости. Парный корреляционный анализ—двух показателей. Множественный корреляционный анализ—более двух показателей. Между показателями должна быть причинная связь. Корреляционный анализ применяется только для случайных величин. Виды зависимости между случайными величинами: 5. функциональная—одному значению случайной величины, распределенной по определенному закону, соответствует одно значение другой случайной величины. 6. вероятностная (стохастическая, статистическая)—при изменении одной случайной величины меняется закон распределения другой случайной величины. 7. корреляционная зависимость—такая вероятностная зависимость, в которой при изменении одной случайной величины изменяется условная средняя другой случайной величины. Любая корреляционная зависимость является, вероятностной, но не любая вероятностная является корреляционной. Виды корреляционной зависимости (функция, которая аппроксимирует закон изменения средней, определяет вид зависимости): 1. если функция линейная, то корреляционная зависимость линейная. 2. если функция не линейная, то корреляционная зависимость криволинейная. Если случайные величины распределены по нормальному закону распределения, то корреляционная зависимость всегда линейная. 16. Коэффициент корреляции, вычисление и границы. Коэффициент корреляции r применятся для измерения степени тесноты связи, только при линейной корреляционной зависимости. Вычисляется по формуле: r xy x y 2 2 ( x 2 x )( y 2 y ) свойства линейного коэффициента корреляции: 1. коэффициент корреляции -1<=r<=1. 2. если коэффициент корреляции r=|1|, то зависимость функциональная. 3. чем больше |r|, тем теснее зависимость между показателями. 4. если r<0, то связь между показателями обратная. 5. если r>0, то связь между показателями прямая. 6. если r=0, то между изучаемыми показателями нет линейной зависимости, но может быть криволинейная корреляционная зависимость причем довольно тесная. 19. Понятие и задачи регрессионного анализа. Регрессионный анализ—раздел математической статистики, объединяющий методы исследования регрессионной зависимости между некоторыми величинами на основе выборочных статистических данных. Регрессионная модель описывает, как в среднем зависит результативный признак У от влияющих на него факториальных признаков Х. на основе регрессионной модели можно определить среднее значение результативного признак У при определенных значениях факториальных признаков. Задачей регрессионного анализа является нахождение таких численных значений оценок параметров регрессии, которые бы не противоречили основным предположениям о свойствах теоретической регрессии. В регрессионном анализе решаются следующие задачи статистического анализа модели: 1. определение точечных оценок (параметров модели). 2. определение статистической значимости оценок. 3. построение доверительных интервалов оценок. 4. проверка адекватности, качества модели в целом. 20. Виды моделей регрессии. Если в модели показывается, что величина У зависит только от одного факториального признака Х, то модель регрессии называется однофакторной, если таких признаков несколько, то модель называется многофакторной. Модель может описывать зависимость величины У от факторов в виде линейной функции (линейная модель регрессии), или в виде той или иной нелинейной функции (нелинейная модель регрессии). Линейная однофакторная модель регрессии имеет вид: У=а0+а1х Линейная многофакторная модель выглядит так: У=а0+а1х1+а2х2+…+акхк Регрессионные модели могут быть представлены полиномами различных степеней: У=а0+а1х+а2х2+… Степенными функциями: У=а0х1а1х2а2… 21. Основные предпосылки регрессионного анализа. 1. У—случайная величина. 2. Хк—независимая переменная. 3. Отсутствие линейной зависимости между факторными признаками (отсутствие явления мультиколлинеарности). 4. Е—случайные независимые величины 5. Е не должны быть автокоррелированы. 6. Должны иметь нормальное распределение с нулевой средней и одинаковой конечной дисперсией. 22. Основные этапы построения модели регрессии. 1. Постановка задачи, определение цели исследования. Чаще всего построить прогноз какого-либо показателя с целью получения опережающей информации для принятия решений. Предполагается, что эти факторы будут влиять и в прогнозном периоде. 2. Анализ информации, установление факторов, влияющих на У. а) на основе экономической теории б) анализ сходных проблем в) здравый смысл 3. Спецификация модели: а) определения вида модели б) отбор факторов, включаемых в модель. 4. Количественная оценка параметров модели на основе метода наименьших квадратов. 5. оценка качества модели: а) оценка качества остатков б) оценка качества коэффициентов регрессии в) оценка качества модели в целом 6. Интерпретация модели и использования для прогнозирования. 23. Задачи анализа остатков в регрессионном анализе. Анализ остатков является одним из этапов проверки качества модели. При выполнении требований к остаткам: 1. Метод наименьших квадратов дает хорошие статистические оценки: оценки отвечают требованиям несмещенности, состоятельности, эффективности. 2. Можно применять аппарат математической статистики для проверки гипотез о значимости этих показателей. Гипотеза проверяется с помощью критериев, которые являются случайными величинами имеющими тот или иной закон распределения. Формулы критериев включают остатки. 24. Анализ качества остатков на основе критерия DW. При помощи критерия DW проверяется наличие автокорреляции в остатках. Проверку осуществляют на основе показателя: n DW (e i 2 i ei 1 ) 2 n e i 1 2 i Значения статистики затабулированы при разных уровнях значимости (0,05) и (0,01). По таблице в соответствии с объемом выборки n и числом включаемых в модель факторов к находятся значения dL и dU. Затем вычисляются значения 4- dL и 4- dU. Если: 1. 2. 0 DW d L --в остатках имеется положительная автокорреляция. 4 d L DW 4 --в остатках имеется отрицательная автокорреляция. 3. 4. dU DW 4 dU --автокорреляция в остатках отсутствует. 4 d U DW 4 d L , --на основе имеющихся данных нельзя установить однозначный ответ. Причина d L DW dU существования автокорреляции может заключаться в ошибке спецификации, когда влияние некоторого существенного фактора или группы факторов оказывается включенным в состав остатка ei. Следовательно, данную проблему можно решить, выявив данный фактор и включив его в модель. Предварительно надо проверить, действительно ли существует зависимость между этим фактором и остатком, или же включить данный фактор в исходную модель и проверить снова автокорреляцию остатков. 25. Графический анализ качества остатков. На основе полученных величин остатков необходимо построить график остатков, отложив на оси абсцисс—номер наблюдения, а на оси ординат—величину остатков. Среди остатков иногда встречается остаток, который по абсолютной величине значительно превосходит остальные остатки. Такие остатки называют выбросами. Так как регрессия характеризует среднюю зависимость между результативным и факториальными признаками, то выброс показывает точку. Которая не совсем типична по отношению к остальным данным. В практических исследованиях рекомендуется отбрасывать точку выброса и данное наблюдение не рассматривать. Графический анализ остатков по расположению «полосы», в которой расположены остатки, позволяет сделать определенные выводы об их свойствах. Так, если остатки заключены в «полосе», параллельной оси абсцисс, то это можно рассматривать как признак того, что выполняется требование постоянства дисперсии. Если «полоса» будет как бы расширяться в ту или в другую сторону, то это означает, что дисперсия непостоянна во времени. В этом случае рекомендуется в модель включить временную компоненту. На графике наглядно будет видно чередование знаков остатков. Что является признаком независимости и случайности остатков. Если имеется достаточно большое количество остатков с одним знаком, то свойство случайности может быть не выполнено, и в дальнейшем может потребоваться пересмотр модели. 29. Коэффициент детерминации как показатель адекватности модели. Для проверки качества модели в целом, оценки того насколько хорошо данная модель описывает фактические данные, используется дисперсионный анализ, на основе которого выводиться коэффициент детерминации R2. Показатель R 2 ( y y) ( y y) 2 , показывающий, какую долю общей вариации составляет объясненная регрессией 2 вариация, служит показателем качества модели и называется коэффициентом детерминации. R2 можно вычислить и по другой формуле: R2 ( y y) 1 ( y y) 2 . 2 Статистическая значимость коэффициента детерминации проверяется по F-критерию, вычисляемому по данным наблюдений по формуле: Fрасч R 2 (n k 1) . (1 R 2 )k Расчетное значение F сравнивается с табличным по таблицам распределения Фишера. Если F расч Fтабл , то R2 статистически значим и модель адекватна. 30. Построение модели регрессии методом последовательного исключения. На начальном шаге строиться регрессионная модель, включающая все факторные переменные. Производится оценка коэффициентов регрессии, для всех коэффициентов определяется t-статистика. Если в построенной модели все t расч t табл и модель адекватна по другим критериям, то из модели исключается только один фактор из данной группы переменных, тот, у которого |tрасч| будет минимальным. Производится пересчет модели регрессии с учетом оставшихся факторных переменных. Снова производится оценка коэффициентов регрессии—так до тех пор пока не будет построена хорошая по статистическим данным модель. Если последующие шаги не улучшают качества модели, то или выбранный набор факторов или выбранная форма модели не удовлетворяют и надо переходить к другой форме или другому набору переменных. 31. Построение модели регрессии методом последовательного включения. Шаг 1. Вычисляются коэффициенты корреляции между всеми имеющимися переменными. На основе полученных коэффициентов корреляции составляется корреляционная матрица. В качестве первой переменной, включаемой в модель, выбирается фактор, имеющий самый высокий коэффициент корреляции с У. Для этой модели вычисляются все статистические показатели качества модели (t-статистика, R2,F). Шаг 2. Вычисляются частные коэффициенты корреляции между всеми факторными переменными, не вошедшими в модель, и У при исключении влияния переменной, вошедшей в модель. В качестве следующего фактора, включаемого в модель, выбирается факторная переменная, имеющая наиболее высокий частный коэффициент корреляции. Проверяется качество, полученной модели. Шаг 3. Процесс продолжается до тех пор, пока включение переменой улучшает качество модели. На каждом шаге одновременно с применением статистических методов оценки качества модели проверяется влияние включенной переменной на коэффициенты регрессии. Если добавление фактора в модель не изменяет существенно коэффициенты регрессии, но увеличивает R2, то он считается полезным; если добавление фактора в модель радикально изменяет все коэффициенты регрессии, но R2 остается без заметного улучшения, то фактор считается вредным.