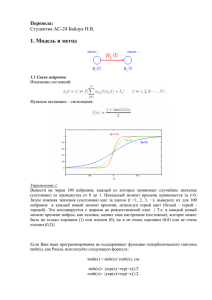
Персептрон с аттракторами

ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
Я. М. КАРАНДАШЕВ
Научно-исследовательский институт системных исследований РАН,
Москва
Yakov.Karandashev@phystech.edu
ПЕРСЕПТРОН С АТТРАКТОРАМИ
Стандартная нейронная сеть Хопфилда, обученная по правилу Хебба,
имеет аттракторы, совпадающие с предъявленными ей паттернами, на
которых обучалась сеть. В отличие от неё, в данной работе исследуется
вопрос о том, возможно ли и как создать нейронную сеть с предсозданными случайными аттракторами, которые никак не связаны с информацией, загружаемой в сеть, но так, чтобы такую сеть можно было использовать как базу для векторного квантования, причём количество задействованных нейронов было бы гораздо меньше числа точек квантования.
Ключевые слова: персептрон, аттракторы, метод молекулярных меток, векторное квантование
Введение
Одним из ключевых аспектов в понимании работы мозга является
формат данных мозга [1]. В данной работе мы переформулировали классический персептрон для случая, когда финальный паттерн имеет нейронное представление в виде дискретного нейросетевого аттрактора. Дискретные нейросетевые аттракторы были впервые описаны Дэвидом Марром в 1971 [2-3] и были интенсивно исследованы после их переоткрытия
Дж. Дж. Хопфилдом в 1982 [4]. Сети с такого рода аттракторами обычно
называются сетями Хопфилда.
В отличие от стандартного подхода к сети Хопфилда, здесь мы рассматриваем сети, построенные с помощью меток, как предложено в [1].
С такой сетью простых нейронов МакКаллока-Питтса мы попытались
сформировать соединения между сетью и внешним набором входов размерности R и произвели обучение по правилу типа правила Розенблатта
для каждого входа и каждого нейрона, так что для различных входных
точек выбирались различные точки аттрактора.

Данная работа выполнена при поддержке АНО «Россия 2045».
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
Описание сети
Схема сети представлена на рис. 1. Вход состоит из R рецепторов, которые через матрицу синаптических весов W передают сигналы на N
нейронов. Эти нейроны связаны друг с другом матрицей синаптических
связей T.
Рис. 1. Общая схема сети
Нейроны с матрицей связей T образуют ассоциативную сеть Хопфилда. В дальнейшем полагаем матрицу T симметричной, а нейроны бинарными, т.е. находящимися лишь в одном из двух состояний: активен si  1
или неактивен si  0 ( i  1, N ). В этом случае, в процессе функционирования, сеть нейронов сходится к устойчивым состояниям, набор и количество которых, вообще говоря, определяется выбором матрицы T.
Динамика нейронной сети. Работа нейронов задаётся динамикой
Хопфилда [4], т.е. нейрон включается, когда суммарный сигнал, пришедший от других нейронов, больше некоторого порога.
Реально, при компьютерном моделировании динамики нейронов, вместо введения порогов, в процессе функционирования искусственно поддерживалась постоянная активность сети, т.е. в каждый момент времени
число активных нейронов L было постоянным.
Мембранный потенциал i-го нейрона рассчитывается как взвешенная
сумма воздействий со стороны активных нейронов:
hi 
N

j 1, j  i
Tij s j , i  1, N .
(1)
Матрица связей T. Метод молекулярных меток. То, в какие аттракторы может прийти нейронная сеть, зависит от матрицы связей нейронов
T. Здесь мы рассмотрим несколько способов получения такой матрицы,
определяющей аттракторы сети.
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
Самым, наверное, простым способом построения матрицы T является
бинаризованное правило Хебба, состоящее в следующем:
1) сгенерируем M N-мерных векторов S m ( m  1, M ), в каждом из которых выбранные случайным образом L координат равны единице, а
остальные N  L элементов равны нулю;
2) в начальный момент все матричные элементы равны нулю ( Tij  0 );
3) просмотрим каждый вектор S m , m от 1 до M и для всех i и j ( i  j ):
если Smi  1 и S mj  1 , то Tij  1 .
если Smi  0 или S mj  0 , то значение Tij не меняется.
В результате получается матрица, симметричная, с нулевой диагональю, и состоящая из нулей и единиц, причем их расположение не зависит
от порядка следования векторов S m .
Недостатком описанного выше построения является создание и хранение набора из M N-мерных векторов S m . В противоположность этому,
был предложен метод молекулярных меток, описанный ниже.
Этот метод получения аттракторов основывается на идее молекулярных меток, присутствующих в генетическом коде нейронов. В отличие от
правила Хебба, описанного выше, в данном методе нет заранее сгенерированных векторов-аттракторов. Напротив, аттракторы получаются как
бы сами собой, в процессе роста сети.
Предположим, что нейроны могут иметь несколько типов молекулярных меток. Пусть число меток, которые имеет нейрон, равно m, а общее
количество различных меток, которые могут быть в принципе, равно M.
Допустим также, что среди нейронов метки распределены случайным образом так, что каждая метка использована строго по L  Nm / M раз.
Принцип работы меток состоит в том, что в процессе роста нейрона,
его аксон образует синапсы с нейронами, имеющими ту же метку, что и
данный нейрон. Тогда группа из L нейронов, имеющих одну и ту же молекулярную метку, оказываются связанными. Именно эта связь обуславливает их взаимное влияние друг на друга, и возбуждение части нейронов
приводит к возбуждению всей группы, т.е. образуется аттрактор.
То же самое происходит с каждой из M меток. В итоге, в сети образуется M аттракторов S m ( m  1, M ), в каждом из которых ровно L нейронов
активно, а остальные неактивны.
Чисто технически, матрица связей T, порождённая метками, состоит
лишь из нулей и единиц, она симметрична и, дополнительно нужно за-
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
дать, чтобы нейроны не образовывали связи сами с собой, тогда матрица
имеет нулевую диагональ.
Нетрудно заметить, что предложенный метод молекулярных меток
очень сильно похож на описанное выше бинаризованное правило Хебба.
На самом деле, итоговые матрицы T, вообще говоря, совпадают. Вся разница лишь в том, какой смысл мы вкладываем в оба метода. Если первый
метод (правило Хебба) традиционно считается правилом обучения на
конкретные паттерны активности, то во втором аттракторы, полученные с
помощью молекулярных меток, оказываются врождённым свойством самой сети нейронов.
Аттракторы нейронной сети. При моделировании асинхронной динамики сети, полученная таким способом матрица T при любой загрузке
(числе M) даёт устойчивые состояния (аттракторы), совпадающие с векторами S m .
Однако при синхронной динамике, начиная с некоторой критической
загрузки M cr , аттракторы перестают быть устойчивыми. На рис. 2 показано, как при увеличении загрузки сети растёт ошибка, т.е. расстояние, на
которое сеть уходит из записанного аттрактора. Расстояние измерено по
Хеммингу и усреднено по всем записанным аттракторам. Из рисунка видно, что до некоторого значения загрузки ошибка нулевая. Дальше, при
превышении критической загрузки, ошибка почти скачком возрастает, что
говорит о потере аттрактора в том месте, где его прописывали.
d 
N  500
600
700
800
900
1000
M
Рис. 2. Экспериментальная зависимость ошибки от загрузки сети для L =
20 при различных размерностях от N=500 до N=1000, для синхронной динамики.
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
На рис. 3 показаны экспериментальные значения критической загрузки cr  M cr / N . Там же построена аппроксимация экспериментальных
точек, полученная по методу минимизации среднеквадратичной ошибки.
Как видно из рисунка, cr растёт линейно с размерностью сети, т.е.
M cr критическая загрузка растёт квадратично по N (при фиксированном
L), и её значение определяется формулой:
M cr  ( N / L) 2 .
(2)
Плотность ненулевых (т.е. единичных) матричных элементов:
(3)
Tij  ML2 / N 2 ,
что, на практике при M  M cr оказывается не больше 0.5.
Когда сеть находится в одном из состояний S m , L нейронов, которые
активны, действуют друг на друга суммарным сигналом, равным:
hact 
N

j 1, j  i
Tij Smj  L  1 .
(4)
M cr / N
y  0.002 N  0.04
N
Рис. 3. Экспериментальная зависимость максимальной загрузки сети от
размерности (показана маркерами) для L = 20; пунктиром показана аппроксимирующая прямая с соответствующим уравнением
Сигнал, приходящий на неактивные нейроны, существенно меньший, это
шум, определяющийся средним значением матричных элементов:
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
(5)
hinact  L Tij  0.5L .
Значит, аттракторы оказываются устойчивыми к шумам порядка 0.5L.
Обучение персептрона
После того как создана аттракторная сеть, т.е. сеть, которая сваливается из любого своего начального состояния в некоторое устойчивое состояние, стоит задача обучения входного слоя весов W, которая определённым образом отображает входные сигналы из R-мерного пространства в
N-мерное. В то же время, аттракторы в N-мерном пространстве делят
между собой всё пространство в соответствии со своей областью притяжения. Данное разбиение, таким образом, может быть использовано для
векторного квантования входных R-мерных сигналов.
В качестве обучающего правила для настройки весов W использовалось персептронное правило Розенблатта [5].
В обычном персептроне Розенблатта обучение происходит следующим
образом. Имеется набор каких-то (может быть случайных) R-мерных векторов X t ( t  1...r ). Присутствует учитель, который ставит в соответствие
каждому входу определённый (желаемый) выход yt ( t  1...r ), принимающий лишь два значения yt  1 . Учитель смотрит, что персептрон выдаёт на выходе
R
ot  Wi X ti ,
i 1
и сравнивает знак выхода с yt . Если выход имеет правильный знак, то
матрица W не изменяется. Если же знаки yt и ot не совпадают, то веса
трансформируются по персептронному правилу Розенблатта:
W  W  X t yt .
Известно, что если точное разделение возможно, то при таком обучении персептрон обучается очень быстро, за несколько итераций (т.е. за
несколько предъявлений всего множества векторов).
Особенностью в данной работе было то, что учителя нет, а значения
yt задаются аттрактором, в который попала нейронная сеть после инициализации её входным вектором. Пусть, например, при подаче вектора X t ,
после прохождения сигнала через матрицу весов W, нейронная сеть получила входной сигнал O  WX t . В результате деятельности нейронов сеть
перешла в некоторое устойчивое состояние S m , в котором какие-то L
нейронов имеют активность 1, а остальные 0.
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
Персептронное правило в этом случае формулируется так: если сигнал
ot , пришедший на нейрон со стороны входа, отрицательный, а нейрон
активен, то к весам, идущим от входа к этому нейрону, прибавляется вектор X t . И наоборот, если сигнал ot , идущий к нейрону со стороны входа,
положительный, а нейрон оказался неактивен, то из вектора весов, идущих от входа к этому нейрону, вычитается вектор X t . В остальных случаях веса не меняются.
Такая процедура повторяется для всех входных векторов X t до тех
пор, пока матрица W не перестанет меняться. В наших экспериментах
обычно было достаточно нескольких итераций (меньше 50).
Известно, что не всегда можно плоскостью разделить множество точек
в пространстве на две наперёд заданные части. Например, если случайные
4 точки в трёхмерном пространстве разделяются плоскостью как угодно,
то 5 пять точек в том же пространстве разделить на две заданные группы
удаётся, увы, не всегда.
Общий результат Э. Гарднер [6] был получен для разбиения на две части с одинаковым числом точек в каждой и заключается в следующем.
Если в R-мерном пространстве случайным образом раскидано не больше
2R точек, и эти точки каким-то образом поровну раскрашены в два цвета
(т.е., например, R красных и R черных), то с вероятностью, стремящейся к
единице при R   , эти точки можно разбить гиперплоскостью на две
части так, что в каждой половине окажутся только точки одного цвета.
Если же число точек больше чем 2R, то вероятность правильного разбиения при R   стремится к нулю.
Видно, что такой результат очень слабый, поскольку говорит о том,
что классифицировать можно максимум лишь 2R точек в R-мерном пространстве. Однако, в той теории ничего не говорилось о делении на две
части не поровну, а отделении небольшой части.
Пусть у нас M точек в R-мерном пространстве. Поставим вопрос о том,
можно ли разделить точки на две части, в одной из которой k точек, а в
другой M-k.
Оказывается, что при небольшом k ( k M / 2 ) число точек M может
быть гораздо больше чем 2R. Был проведён эксперимент (рис. 4), из которого была получена приближённая формула:
R
(6)
M  0.5 R e 2k .
Это показывает, что число паттернов M при фиксированном k растёт
экспоненциально от R.
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
В нашем случае k  ML / N и составляет обычно порядка 0.01M.
Число рецепторов (размерность входа) R может быть произвольной. В
экспериментах мы брали R  100...500 .
M /R
R
Рис. 4. Экспериментальная зависимость максимального числа точек M,
которые ещё можно линейно разделить на две случайные группы с k и M-k
точек, от размерности пространства R. Эксперименты проводились для k =
10, 50, 75
и 100, линейное разбиение производилось с помощью алгоритма Розенблатта; пунктиром показаны аппроксимирующие прямые с соответствующими уравнениями; вертикальная ось показана в логарифмическом
масштабе
Эксперименты
Приведём примеры того, как реально обучается сеть при подаче на неё
случайных входных векторов.
Пусть мы создали сеть с некоторыми параметрами. Пусть также число
подаваемых паттернов на сеть равно числу аттракторов, созданных в
нейронной сети.
Подадим на вход поочерёдно паттерны и запомним те аттракторы, в
которые сошлась сеть при их предъявлении. Если не производить никакого обучения, то при подаче тех же, но зашумлённых паттернов, сеть, вероятно, сойдётся уже в другие аттракторы. На рис. 5 слева показано, как
растёт среднее расстояние сдвига от исходного аттрактора при увеличении шума. Шум измеряется как расстояние Евклида от исходного паттерна до зашумлённого.
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
На рис. 5 справа показана та же величина сдвига, только после обучения («с аттракторами»). При этом было интересно также пронаблюдать, а
что будет, если отключить рекуррентные связи и выделять лишь L победителей (без аттракторного восстановления). Как видно, сеть с аттракторами обладает гораздо большей помехоустойчивостью (при данных параметрах вплоть до 50 %-го шума), чем без аттракторов (шумы не больше
10%). Необученная сеть практически вообще не обладает устойчивостью
(шумы менее 0.1%).
d 
d 
без аттракторов
с аттракторами


Рис. 5. Средний сдвиг (расстояние по Хеммингу) как функция от величины шума: слева – до обучения, справа – после обучения; R = 100, N = 300,
M = 100, L = 20
Аналогичные эксперименты проводились при других параметрах сети.
Результаты были схожи. Обучение всегда заканчивалось менее чем за 50
итераций.
Заключение
Обучение аттракторных нейронных сетей Хопфилда обычно производится по правилу Хебба. Мы обнаружили, что сети с той же общей структурой аттракторов могут быть получены с помощью некоторого количества типов меток, которые некоторым случайным образом распределяются равномерно между N нейронами. Нейроны с одинаковыми метками
соединяются возбуждающими связями.
Сеть с такой структурой была использована нами для представления
выхода персептрона в виде устойчивого паттерна активности нейронов.
В результате мы получили следующий результат: для входов, представляющих собой несвязанные сигналы из разных областей R-мерного
ISBN 978-5-7262-1773-4 НЕЙРОИНФОРМАТИКА-2013. Часть 1
входного пространства, было получено отображение на дискретные аттракторы, причём с чётким разграничением между аттракторами, соответствующим разным категориям входных векторов.
Одной из важных черт данного принципа обучения является то, что
количество паттернов, которые нейронная сеть может идентифицировать,
будет расти как N^2 (при фиксированном числе одновременно активных
нейронов L). Для N = 10000…50000 нейронов и L = 20…50 мы получим
M = 200000…1000000 точек аттракторов.
Фактически мы получили, что одни и те же нейроны оказываются задействованными по нескольку раз. Таким образом, решается проблема
избыточности сетей Кохонена [7]. Предложенные в работе аттракторы
можно рассматривать как виртуальные нейроны, использующиеся как
ячейки карт Кохонена.
Список литературы
1. В.Л. Дунин-Барковский. Бугорковые аттракторы и понимание механизмов мозга. // Труды конференции «Нелинейная динамика в когнитивных исследованиях-2011». ИПФ РАН. Нижний Новгород, 2011. С. 5356.
2. Marr D. Simple Memory: A Theory for Archicortex. //Philosophical
Transactions of the Royal Society of London. Series B, Biological Sciences,
1971. V. 262. No. 841. Р. 23-81.
3. Дунин-Барковский В.Л. Нейронные схемы ассоциативной памяти.
// Моделирование возбудимых структур./ Под ред. В.И. Крюкова. АН
СССР, Научный центр биологических исследований. Пущино, 1975. С. 90141.
4. Hopfield J.J. Neural networks and physical systems with emergent collective computational abilities. //Proc. NatL Acad. Sci. USA, 1982. V. 79. Р.
2554-2558.
5. Розенблатт Ф. Принципы нейродинамики: Перцептроны и теория
механизмов мозга//Principles of Neurodynamic: Perceptrons and the Theory
of Brain Mechanisms. М.: Мир, 1965.
6. Hertz J., Krogh A., Palmer R. Introduction to the theory of Neural Computation //Redwood City: Addison-Wesley, 1991.
7. T. Kohonen. Learning Vector Quantization// Neural Networks, 1988. 1
(suppl 1). Р. 303.