Основы теории управления: конспект лекций. Часть 2

3 Устойчивость линейных систем
Устойчивость – это свойство системы возвращаться в прежнее
состояние равновесия после вывода ее из этого состояния и прекращения
этого действия в системе.
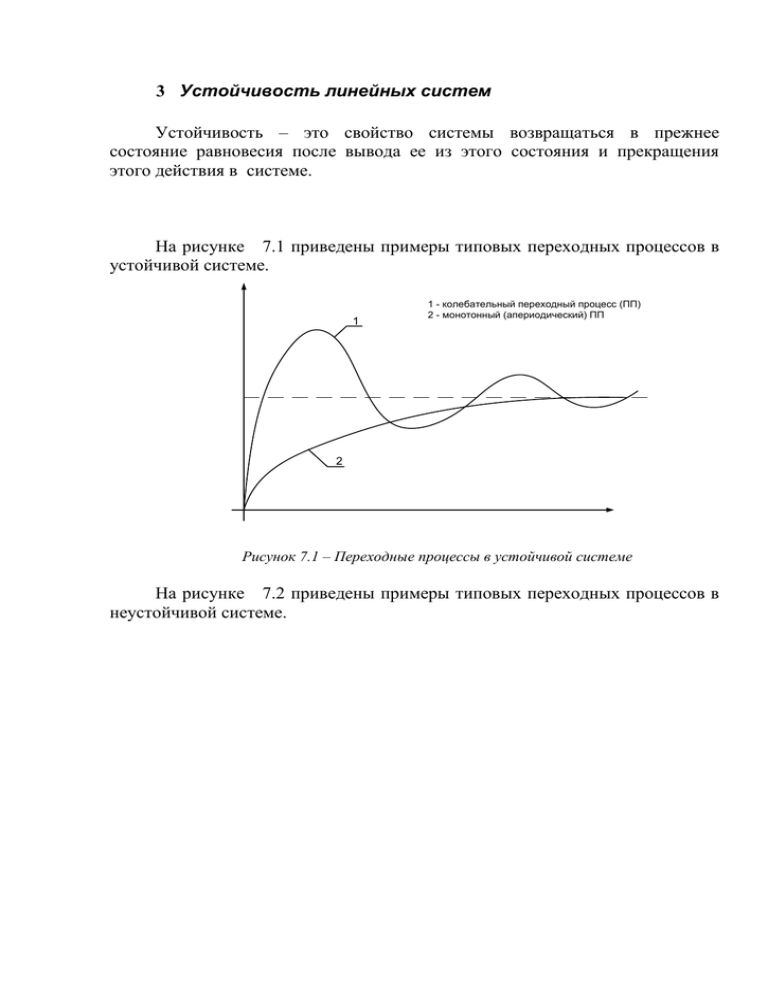
На рисунке 7.1 приведены примеры типовых переходных процессов в
устойчивой системе.
1
1 - колебательный переходный процесс (ПП)
2 - монотонный (апериодический) ПП
2
Рисунок 7.1 – Переходные процессы в устойчивой системе
На рисунке 7.2 приведены примеры типовых переходных процессов в
неустойчивой системе.
2
1 - колебательная неустойчивоать
2 - апериодическая устойчивость
1
Рисунок 7.2 – Переходные процессы в неустойчивой системе
7.1 Условия асимптотической устойчивости системы
Пусть для исходной системы найдена передаточная функция в
замкнутом состоянии.
B(p) bm p m  bm1 p m1  ...  b1 p b 0 Y ( p)
Wз (p) 


,
A(p) an p n  an1 p n1  ...  a1 p  a 0 V ( p)
(7.1)
где b j =const , j= 0, m , a j =const, , i= 0, n
На основе (7.1) можно записать операторное уравнение
an p nY ( p)  an1 p n1Y ( p)  ...  a1 p Y ( p) a 0Y ( p) 
 bm p mV ( p)  bm1 p m1V ( p)  ...  b1 p V ( p) b0V ( p).
(7.2)
Используя свойства преобразования Лапласа можно записать линейное
дифференциальное уравнение n-го порядка.
an y
(n)
 an1 y
( n 1)

 ...  a1 y  a 0  bm v
( m)
 bm1v
( m 1)

 ...  b1 v b0 v
y0  y (t  0);


(k )
y0  y k (t  0);

k  1, (n  1).

(7.3)
Решение дифференциального уравнения (7.2) может быть представлено
в виде:
y  y b  y cb ,
(7.4)
b
где y – вынужденная (полезная) составляющая, определяется правой
частью уравнения (7.2),
y cb
– свободная (переходная) составляющая, определяется
решением однородного дифференциального уравнения, т.е. с правой частью.
Вид переходного процесса в исследованной системе определяется
корнями характеристического уравнения замкнутой системы, т.е. A( p)  0
или:
an p n  an 1 p n 1  ...  a1 p  a0  0.
(7.5)
Система асимптотически устойчива, если выполняется условие
Lim y cb 0.
(7.6)
t 
Для доказательства можно рассмотреть два случая:
1) Пусть характеристическое уравнение (7.5) имеет действительные не
кратные корни:
pk  0,
k  1, n.
Из математики известно, что:
n
ycb   ck c p k t .
k 1
(7.7)
Следовательно:
n
ycb   ck c p k t  0,
k 1
pk  0,
k  1, n.
Пусть:
pk   k ,
 k  0.
(7.8)
При выполнении условия (7.8) система асимптотически устойчива (см.
рисунок 7.3).
Im
p3 p2 p1
Рисунок 7.3 – Асимптотически устойчивые системы
Пусть характеристическое уравнение (7.5) имеет s действительных
корней и n-s корней комплексно-сопряженных:
pk    k ,
k  1, S ;
p k   k  ji ,
i  1,
ns
;
2
причем, n-s всегда четно.
Тогда можно записать:
S
Lim ( C e
t 
k 1
bkt
k
ns
2
  C k e  it  sin( i t   i ))  0.
(7.9)
i 1
Формула (7.9) выполняется при условии:
 k  0, k  1, s,
 k  0, i  1,
ns
.
2
(7.10)
Пусть рассматривается система четвертого порядка (n=4) и пусть
характеристическое уравнение имеет следующие корни:
p3   1 ,
1  0,
 k  0,
p4    2 ;
k  1,2;
p1, 2  1  j1 ,
 2  1  1.
Тогда с учетом (7.10) расположение корней на комплексной плоскости
имеет вид представленный на рисунке 7.4
Im
p1
1
 1
Re
  2  1
p2
 1
Рисунок 7.4 – Расположение корней на комплексной плоскости
Таким образом, на основе (7.10) можно сделать вывод: линейная
система асимптотически устойчива если все корни асимптотические
уравнения располагается в левой полуплоскости, комплексной плоскости
корней. Если хотя бы один действительный корень или пара комплексносопряженных корней располагаются на мнимой оси, то такая система
находится на границе устойчивости.
Если хотя бы один корень находится в правой полуплоскости, то в
соответствии с (7.9) и (7.10), система является неустойчивой.
7.2 Необходимые условия устойчивости системы
Пусть для структурной схемы рассматриваемой системы найдена
передаточная функция в замкнутом состоянии:
Wз (p) 
b0
.
an p n  an1 p n1  ...  a1 p  a 0
(7.11)
Aз (p)  an p n  an1 p n1  ...  a1 p  a 0 .
(7.12)
Характеристическое уравнение:
Aз (p)  0
или
an p n  an1 p n1  ...  a1 p  a 0  0.
(7.13)
Пусть характерное уравнение (7.13) имеет корни pi , i  1, n.
Из математики известно, что характерный полином (7.12) можно
разложить на множители:
Aз (p)  an ( p  p1 )( p  p2 )...( p  pn ).
Пусть характерное
отрицательные корни:
уравнение
(7.13)
(7.14)
имеет
pk   k ; k  1, n;  k  0.
действительные
(7.15)
Тогда (7.14) с учетом (7.15) можно записать в виде:
Aз (p)  an ( p  1 )( p   2 )...( p   n ).
(7.16)
Поскольку все сомножители в формуле (7.16)
являются
положительными, следовательно, и коэффициенты характеристического
уравнения (7.13) также являются положительными.
Утверждение 2:
Необходимым условием устойчивости является
положительность корней всех коэффициентов характеристического
уравнения.
Пусть уравнение (2.13) имеет два комплексных корня и n-2
действительных корня:
p1, 2  1  j1 , 1  0.
(7.17)
n  2, pk   k , k  1, n  2.
(7.18)
На основе (7.17) и (7.18) можно записать:
Aз (p)  an ( p  1  j1 )( p  1  j1 )( p  1 )...( p   n2 ) 
 (an ( p  1 ) 2  12 )( p  1 )...( p   n2 ).
(7.19)
Таким образом, и в данном случае коэффициенты характеристического
уравнения так же оказываются положительным, что и требовалось доказать.
Если хотя бы один коэффициент характеристического уравнения не
являются положительным, то в соответствии с доказанным утверждением
вторая рассматриваемая система не является устойчивой.
7.3 Критерий устойчивости линейных систем
Находить корни характеристического уравнения высоких степеней
затруднительно или невозможно, а численные методы надают общего
решения, поэтому используют косвенные методы анализа устойчивости
систем.
Критерием устойчивости называют правила позволяющие сделать
вывод
об
устойчивости
системы,
без
определения
корней
характеристического уравнения.
Критерии устойчивости как косвенные методы делятся на две группы:

алгебраические критерии устойчивости,

частотные критерии устойчивости.
7.3.1 Алгебраический критерий Гурвица (1895 г.)
Пусть найдено характеристическое уравнение (7.5).
Из коэффициентов (7.5) состоится главный определитель Гурвица n-го
порядка.
n 
an 1
an
0
an 3
an  2
an 1
an 5
an  4
an  3
an 7 ... ...
an 6 ... ...
an 5 ... ...
...
...
...
0
0
0
0
0
0
0
0
an
0
0
0
0
an  2
an 1
an
...
0
an  4
an 3
an  2
...
...
...
...
...
a1
a2
0
0
0
0
a0
...
...
...
...
...
...
...
...
a3
a4
Система устойчива, если при An>0 все определители Гурвица являются
положительными.
0, n  0,
1  an1  0,
 2  an1an2  an an3
...
 n  a0  n1  0.
1)
2)
3)
4)
5)




 0,




(7.20)
Этапы анализа устойчивости по критерию Гурвица:
Если дана структурная схема исходной системы, то после
соответствующих структурных преобразований можно найти Wз(p)передаточная функция системы в замкнутом состоянии.
Приравнивая Wз к 0 записывают характеристическое уравнение
системы.
После обозначения коэффициентов характеристического уравнения
составляется главный определитель Гурвица n .
Если условие (7.20) выполняется, то такая система является устойчивой.
Если все определители Гурвица положительны, а  n  0 , то такая
система находится на границе устойчивости.
an  a0  n 1  0.
Приведем два случая:
1)
При a0  0 и  n 1  0 в системе появляется нулевой корень (p=0),
что соответствует апериодичной границе устойчивости.
2)
При  n 1  0 , a0  0 - соответствует колебательной границе
устойчивости.
При использовании критерия Гурвица передаточная функция замкнутой
системы имеет вид:
Wз ( p) 
B( p)
.
A( p)
1) Пусть
исходная
система
представляется
инерционным звеном первого порядка вида:
Wз ( p ) 
пропорциональным
b0
K

.
Tp  1 a1 p  a0
Система устойчива, если:
 a1  0,
 1  d 0  0.
2) Пусть исходная система - пропорциональное звено второго порядка с
ПФ.
b0
K
Wз ( p )  2 2

,
2
T p  2dTp  1 a2 p  a1 p  a0
2
где b0  k , a2  T , a1  2dT , a0  1.
Характеристическое уравнение имеет вид:
a2 p 2  a1 p  a0  0.
Система устойчива, если:
a
2  1
a2
0
a0
 a2  0
 1  a1  0
  2  a0 1  a0 a1  0
Т.е. a1  0 , то и должно быть a0  0.
Окончательно можно записать:
a 2  0,
a1  0,
a 0  0.
Таким образом, для систем первого и второго порядков
положительность коэффициентов ХУ – необходимое и достаточное условие
устойчивости.
3) Дана система 3-го порядка с ПФ в ЗС вида:
Wз ( p ) 
b0
.
a3 p 3  a 2 p 2  a1 p  a0
Характеристическое уравнение системы в замкнутом состоянии имеет
вид:
a3 p 3  a2 p 2  a1 p  a0  0.
Главный определитель Гурвица:
a 2 a0 0
 3  a3
0
a1
a2
0
a0
Система устойчива, если:
a3  0,
1  a2  0,
 2  a1a2  a0 a3  0,
 3  a0  2  0 , следовательно, a0  0.
Поскольку a0  0 , то a1  0 .
Окончательно можно записать
a0  0,
a1  0,
a2  0,
a3  0,
 2  a1a2  a0 a3  0.
Таким образом, для устойчивости системы третьего порядка в
дополнение к необходимым условиям устойчивости (положительность
коэффициентов характеристического уравнения) должно быть и
 2  a1a2  a0 a3  0 .
4) Дана схема вида (см. рисунок 7.4):
V ( p)
K1
T1 p  1
K 2
T2 p  1
Y (p)
K3
T3 p  1
Рисунок 7.4 – Структурная схема системы
Все параметры звеньев системы являются положительными.
Wз ( p ) 



W(p) пц
1  W(p) пц W(p) ос
K1K 2 K 3
(T1p  1)(T2 p  1)(T3 p  1)


K1K 2 K 3
1
(T1p  1)(T2 p  1)(T3 p  1)
K1K 2 K 3

(T1p  1)(T2 p  1)(T3 p  1)  K pc
K pc
T1T2 T3 p 3  (T1T2  T1T3  T2 T3 )p 2  (T1  T2  T3 )p  K pc  1
K pc
a3 p 3  a 2 p 2  a1 p  a0
(7.21)

,
где K pc  K1K 2 K 3 – передаточный коэффициент разомкнутой системы.
a3  T1T2 T3  0,
a2  T1T2  T1T3  T2 T3 ,
a1  T1  T2  T3 ,
a0  K pc  1.
Характеристическое уравнение системы в замкнутом состояние:
a3 p 3  a2 p 2  a1 p  a0  0.
(7.22)
Пусть требуется найти расчетную формулу граничного значения
передаточного коэффициента разомкнутой системы.
Главный определитель Гурвица при n=3:
a2 a0 0
 3  a3 a1 0
0 a2 a0
a3  T1T2T3  0 ,
1  a2  T1T2  T1T3  T2T3  0.
(7.23)
В соответствии с критерием Гурвица система находится на границе
устойчивости при условии:
 3  a0  2  0,
a0  K pc  1  0,
 2  a1a2  a0 a3  (T1T2  T1T3  T2T3 ) 
 (T1  T2  T3 )  T1T2T3 (K гpc  1)  0.
Формула для расчета:
(T1T2  T1T3  T2 T3 )T3 (1 
K гpc 
T1 T2
 )
T3 T3
T1T2 T3
1 
(7.24)
T
T
T T
 (1  3 .  3 )(1  1  2 )  1
T1 T2
T3 T3
Пусть
1 
T1
T1
, а 2 
, следовательно, можно записать:
T3
T3
K гpc  (1   1   2 )(1 
1

1
1  2
)  1.
(7.25)
Таким образом, K гpc зависит от соотношения между постоянными
времени.
7.3.2 Частный критерий Михайлова
Доказательство критерия основывается на принципе аргумента.
Пусть найдена передаточная функция системы в замкнутом состоянии:
b0
B( p)
Wз ( p ) 

.
(7.26)
n
n 1
an p  an1 p  ...  a1 p  a0 Aз ( p)
Пусть характеристическое уравнение выглядит следующим образом:
an p n  an1 p n1  ...  a1 p  a0  0.
(7.27)
pk , k  1, n.
(7.28)
Тогда характерный полином замкнутой системы может представить в
виде:
Aз ( p)  an p n  ...  a0  an ( p  p1 )( p  p2 )...( p  pn ).
(7.29)
Требуется определить условия, при которых все корни уравнения (7.27)
при которых уравнение (2.27) располагается в левой плоскости комплексной
плоскости корней.
При p  j можно записать характеристический вектор в виде:
Aз ( j )  an ( j  p1 )( j  p2 )...( j  pn ) 
 an A1 ( )e j1 ( ) an A2 ( )e j2 ( ) ...an An ( )e jn ( ) 
 Wз ( p)  A( )e
j (  )
(7.30)
,
n
где A( )  an  Ak ( ) ,
k 1
n
 ( )    k ( ) .
k 1
Пусть характеристическое уравнение (7.27) имеет действительные
отрицательные корни.
1) pk   k , k  0, k  1, n .
(7.31)
Условия
(7.31) соответствует устойчивой системе. Рассмотрим
элементарный вектор (см. рисунок 7.5):
j
j
k
P
Im
Re
Pk
Рисунок 7.5 – Элементарный вектор устойчивой системы
При изменении частоты  от 0 до  , элементарный вектор
повернется против часовой стрелки, то есть в положительном направлении на
угол =

, что соответствует первому квадранту.
2
Тогда окончательно можно записать:
Arg Aз ( )

0

n .
2
(7.32)
2) Пусть характеристическое уравнение (7.27) содержит два
комплексно-сопряженных корня, а остальные корни действительные и
отрицательные (см. рисунок 7.6).
p1, 2  1  j1 , 1  0,
pk    k ,  k  0, k  1, n  2.
j
p1
 1
p2
 p1
1
Im
j
2
Рисунок 7.6 – Корни уравнения (7.27)
Рассмотрим два вектора. Таким образом, окончательно можно записать:
Arg Aз ( j ) 

2
 1 

2
 2  (n  2)
 из подобия   ов  1   2  n

2

2

(7.33)
.
Годографом Михайлова называется геометрическое место конца
вектора Aз , при изменении частоты от 0 до  .
Критерий Михайлова.
Система управления n-го порядка устойчива, если годограф Михайлова
пройдет последовательно против часовой стрелки n квадрантов, начинаясь на
вещественной положительной полуоси.
Если система удовлетворяет критерию, то она является устойчивой, что
соответствует расположению корней характеристического уравнения в левой
полуплоскости комплексной плоскости корней.
Если хотя бы 1-н корень не находится в левой полуплоскости, то
критерий устойчивости Михайлова выполнятся не будет и такая система не
является устойчивой.
На рисунке 7.7 приведены примеры годографа Михайлова устойчивых
систем.
Im
n=2
n=1
n=3
n=5
Re
0
 0
n=4
Рисунок 7.7 – Годографы Михайлова устойчивых систем
7.3.3 Частотный критерий Найквиста (1932 г.)
Критерий является наиболее распространенным при анализе
устойчивости систем. Критерия Найквиста позволяет сделать вывод об
устойчивости замкнутой системы по
частотным характеристикам
разомкнутой системы. Исходная система управления должна быть приведена
к одноконтурной структурной схеме вида (см. рисунок 7.8):
V(p)
W pc ( p )
Y(p)
Рисунок 7.8 – Одноконтурная структурная схема системы
Пусть дана передаточная функция разомкнутой системы:
B( p) bm p m  ..  b1 p  b0
W pc ( p) 

,
C ( p) cn p n  ..  c1 p  c0
где m  n;
(7.34)
b j  const , j  1, m;
ci  const , i  1, n.
Тогда передаточная функция замкнутой системы имеет вид:
B( p)
W pc ( p)
B( p)
B( p)
C ( p)
Wз ( p ) 




1  W pc ( p) 1  B( p) C ( p)  B( p) Aз ( p)

C ( p)
G( p)
(7.35)
bm p m  ..  b1 p  b0

.
an p n  ..  a1 p  a0
Доказательство критерия основывается на анализе вспомогательной
функции:
B( p) C ( p)  B( p) Aз ( p)
G( p)  1 


.
(7.36)
C ( p)
C ( p)
C ( p)
Характеристический полином разомкнутой системы:
C (p)  C n p n  ..  C1 p  C0 .
(7.37)
Aз (p)  An p n  ..  A1 p  A0 .
(7.38)
Пусть корни характеристического уравнения разомкнутой системы
имеют вид:
C n p n  ..  C1 p  C0  0,
(7.39)
pi' , i  1, n.
Пусть корни характеристического уравнения замкнутой системы:
a(p)  an p n  ..  a1 p  a0  0,
(7.40)
pi , i  1, n.
Разложив полином числитель и знаменателя на многочлены (7.36)
можно записать:
a ( p  p1 )( p  p2 )...( p  pn )
G ( p)  n
.
(7.41)
cn ( p  p1' )( p  p2' )...( p  pn' )
При p  j на основе (7.41) можно получить вектор вида:
an ( j  p1 )...( j  pn ) A( )e j ( )
G ( p) 

'
,
cn ( j  p1' )...( j  pn' ) C ( )e j ( )
n
где  ( )   k ( ),
k 1
n
 ' ( )   ' k ( ), i  1, n.
(7.42)
k 1
Пусть система в разомкнутом состоянии является устойчивой, т.е. в
левой полуплоскости комплексной плоскости корней.
Пусть система в замкнутом состоянии имеет n-s корней в левой и s
корней в правой полуплоскости, тогда в соответствии с принципом аргумента
можно записать:
Arg G ( j )

 (n  s)
0

2
s

2
n

2
 s .
(7.43)
Поскольку замкнутая система должна быть устойчивой то, s=0
следовательно:
Arg G ( j )
и,

 0.
(7.44)
0
На рисунке 7.9 приведена G ( j ) при изменении частоты от 0 до  .
Im
 0
1
0
Re
Woc ( j)
G( j)
Рисунок 7.9 –График G ( j ) при изменении частоты от 0 до

Условие (7.44) справедливо, если годограф этого вспомогательного
вектора при изменении частоты от 0 до  не охватывает начало коэффициент.
Поскольку в теории управления принято судить об устойчивости
замкнутой системы по характеристикам разомкнутой, то на основе (7.44)
можно записать:
G ( j )  1  W pc ( j ).
(7.45)
Формулу (7.45) можно записать следующим образом:
W pc ( j )  G ( j )  1.
(7.46)
На рисунке 7.10 приведена АФЧХ разомкнутой системы
Im
 0
(1, j 0)
 0
Re
n=4
Woc ( j)
Рисунок 7.10 – АФЧХ разомкнутой системы
Формулировка критерия: если система в разомкнутом состоянии
является устойчивой, то для устойчивости замкнутой системы необходимо и
достаточно чтобы годограф АФЧХ РС при изменении частоты от 0 до  не
охватывал особую точку с координатами (1, j 0) .
7.4 Понятие статических и астатических систем
1) Статические системы
Пусть система приведена к одноконтурной системе путем структурных
преобразований вида (см. рисунок 7.11):
V(p)
W1 ( p )
W2 ( p )
  
Wn ( p)
Y(p)
Рисунок 7.11 –Одноконтурная структурная схема системы
Если одноконтурная структурная схема не содержит интегрирующего
звена, то ее называют статической.
Пусть схема состоит из n пропорциональных инерционных звеньев 1-го
порядка, тогда можно записать:
W1 ( p ) 
Ki
.
Ti p  1
n
n
i 1
i 1
Wpc ( p)  Wi ( p)  
Ki
.
Ti p  1
(7.47)
Рассмотрим частотную передаточную функцию вида:
Wpc ( j)  A() e j ( ) ,
(7.48)
n
Ki
где A( )  
Ti   1
2
i 1
2
,
n
 ( )   arctg (Ti ),
(7.49)
 ( )  0.
Lim

(7.50)
i 1
0
Следовательно, годограф АФЧХ, при   0 ,
вещественной положительной полуоси (см. рисунок 7.12).
начинается
на
Пусть n=3
Im
1
2
1 - устойчивая система
2 - на границе устойчивости
3 - не устойчивая
3

(1, j0)



Re
Рисунок 7.12 –Примеры АФЧХ разомкнутых систем
2) Астатические системы
Если одноконтурная структурная схема содержит одно интегрирующее
звено, то ее называют асимптотической системой первого порядка.
Пусть одноконтурная структурная схема содержит одно интегрирующее
звено и n-1 пропорциональное инерционное звено первого порядка. Тогда на
основе (7.49) можно записать:
 ( )  
Lim

0

2
n
  (arctg (Ti )),
i 2

 ( )   .
2
(7.51)
(7.52)
Примеры годографа АФЧХ астатической системы первого порядка (см.
рисунок 7.13).
Im
1 - устойчивая система
2 - на границе устойчивости
3 - не устойчивая
Re

(1, j0)
3
2
1
Рисунок 7.13 –Годограф АФЧХ астатической системы первого порядка
7.5 Понятие устойчивости по модулю и фазе
Пусть рассматривается статическая система третьего порядка, тогда на
рисунке 7.14 можно привести АФЧХ системы.
Im
A(п )
(1, j 0)



A(0)

 0
k pc

 (cp )

A(cp )
Рисунок 7.14 – АФЧХ системы третьего порядка
Наличие особой точки с координатами (1, j 0)
необходимости рассмотрения окружности единичного
соответствующих показателей.
приводит к
радиуса и
1) Запас устойчивости по модулю
Пусть  ( )   , следовательно рассматриваемый вектор A( )
система тем дальше находится от границы устойчивости, чем меньше A( ) .
Коэффициент запаса устойчивости по модулю рассчитывается по
формуле:
 зу 
1
,
A( )
(7.53)
где  показывает, во сколько раз можно увеличить
устойчивую систему вывести на границу устойчивости.
K pз , чтобы
Пусть A( )  0.5 , следовательно  зу  2 .
Как правило  зу  2.5 .
Запас устойчивости по модулю можно рассчитывать в децибелах.
20 Lg  зу  20 Lg
1
 20 Lg ( A( )).
A( )
(7.54)
Запас устойчивости по фазе.
Пусть A(cp )  1 .
5)
Если   cp , то A( )  1 , следовательно, такие
сигналы
передаются в системе от входа на выходе с затуханием на амплитуде и
говорят, что они “срезаются” по амплитуде.
3)
4)
Запас устойчивости по фазе вычисляется по формуле:
     (cp ) , рад;
(7.55)
 0  180   0 (cp ) , град.
Если   0 , то такая система является устойчивой.
0
0
Если система неустойчива, то  (cp )  180 , следовательно   0 .
7.6 Построение логарифмических
разомкнутых систем
частотных
Дана структурная схема системы (см. рисунок 7.15):
характеристик
k1
T1 p  1
V(p)
k2
T2 p  1
Y(p)
Рисунок 7.15 –Структурная схема системы
Исходные данные:
K 1  100;
T1  1c;
K 2  1;
T2  0.1c.
K pc  K1K 2  100 , тогда на рисунке 7.16 можно привести
Пусть
структурную схему систему.
k pc
V(p)
T2 p  1
1
T2 p  1
Y(p)
Рисунок 7.16 –Структурная схема системы
Логарифмические
характеристики
инерционного звена первого порядка:
для
20LgK pc , при   с1 ,
L1 ( )  
20LgK pc  20Lg T1 , при    с1 ;
L10  20Lg100  40 дб;
L 20  20Lg1  0 дб;
с 
1
 1c 1 ;
T1
с 
1
 10c 1 ;
T2
1
2
Lg  с1  0;
Lg  с2  1.
пропорционального
На рисунке 7.17 изображены логарифмические амплитудочастотная и
фазочастотная характеристики системы.

L( ) дБ
40
20
lg()
1
3
2
-90
-180
Рисунок 7.17 – Логарифмические амплитудочастотная и фазочастотная характеристики
системы
  180   (cp )  22.
На рисунке 7.18 изображена АФЧХ системы.

Im
A(cp )
Re
Рисунок 7.18 АФЧХ системы
2)Дана структурная схема системы (см. рисунок 7.19).
W1 ( p )
W2 ( p)
k pc
1
T2 p  1
V(p)
T2 p  1
W3 ( p )
1
p
Y(p)
Рисунок 7.19 –Структурная схема системы
K pc  K1 K2  100;
W ( p) 
1
.
p
W ( j ) 
A( ) 
T1  1 c;
1
c 
1
;  
1
 1c 1.
T1
c  10c 1.
 1
 j   .
j
 
1
2
lg c1  0.

lg c2  1; A(cp )  1.
.
2
L( )  20 lg A( )  20 lg

T1  0,1 c.
На рисунке 7.20 изображены логарифмические амплитудочастотная и
фазочастотная характеристики.

L( ) дБ
40
20
lg()
1
2
3
-90
-180
-270
Рисунок 7.20 –Логарифмические амплитудочастотная и фазочастотная характеристики
4 Устойчивость линейных систем
Так как, как правило, исходная система при заданных параметрах
является неустойчивой, то необходима коррекция динамических свойств
системы.
8.1 Расчет параметров корректирующего устройства
Схема решающего блока (РБ), выполняющего функции коррекции
динамических свойств исходной системы приведена на рисунке 8.1.
C0
C1
R0
R1
R0
R1
1
V
2
xРБ
Рисунок 8.1 – Схема корректирующего устройства
Схема описывается следующей передаточной функцией:
1
C0 p
1
R1 
C0 p
1
R1
C1 p
1
R1 
C1 p
R0
WРБ (1) 
где
Z 0 ( p)

Z1 ( p)
T0  R0C0 p  1,
R
k РБ  0 ,
R1
T4  R1C1 p  1.

R0 R1C1 p  1
T p 1

 k РБ 4
,
R1 R0C0 p  1
T0 p  1 (8.1)
8.2 Передаточная функция скорректированной
управляющему и возмущающему воздействию
системы
по
Структурная схема скорректированной системы приведена на рисунке
8.2.
Z ( p)
(Tp  1)k Z
(T2 p  1)(T3 p  1)
()
V ( p)
k РБ
T4 p  1
T0 p  1
k1
T1 p  1
k0
T2 p  1
Y ( p)
1
T3 p  1
()
kОС
Рисунок 8.2 –Структурная схема скорректированной системы
В соответствии с теорией управления можно принять;
T4  T1 ,
T0  0,1T3.
(8.2)
1) Пусть Z=0, тогда передаточная функция скорректированной системы
по управляющему воздействию с учетом (8.2) имеет вид:
T
k РБ
k1k0
T
(T2 p  1)(T3 p  1)(T0 p  1)
k РБ
k1k0
WZC1 ( p) 

, (8.3)
T
T
k РБ
k1k0
(T2 p  1)(T3 p  1)(T0 p  1)k РС
1
(T2 p  1)(T3 p  1)(T0 p  1)
T
T
где k РС  k РБ k1k0 k РС . ,
2) Пусть входной сигнал не изменяется, следовательно, V=0, тогда
передаточная функция скорректированной системы по возмущающему
воздействию имеет вид:
(Tp  1)k Z
(T2 p  1)(T3 p  1)
WZC1 ( p ) 

T
k РС
1
(T2 p  1)(T3 p  1)(T0 p  1)


(Tp  1)(T0 p  1)k Z
Y ( p)

.
(T2 p  1)(T3 p  1)(T0 p  1)  k РС Z ( p )
(8.4)
Характеристической уравнение скорректированной системы имеет вид:
T
T3T2T1 p 3  (T2T3  T2T0  T3T0 ) p 2  (T2  T3  T0 ) p  k РС
 0. (8.5)
8.3 Расчет переходного процесса в скорректированной системе
На основе (8.4) можно записать операторное уравнение:
T3T2T0 p 3  Y ( p )  (T2T3  T2T0  T3T0 ) p 2  Y ( p ) 
T
 (T2  T3  T0 ) p  Y ( p )  (k РС
 1)Y ( p ) 
 (TT0 p  (T  T0 ) p  1)k Z Z ( p ).
(8.6)
2
Пусть f= -Z, тогда на основе (8.6) можно записать уравнение в
символической форме:
a3 p 3 y  a2 p 2 y  a1 py  a0 y  b2 p 2 f  b1 pf  b0 f ,
где
a3  T3T2T0 ,
a2  (T2T3  T2T0  T3T0 ),
a1  (T2  T3  T0 ),
T
a0  (k РС
 1),
b2  TT0 k Z ,
b1  (T  T0 )k Z ,
b0  k Z .
На основе (8.7) можно записать:
a3 p 3 y  p 2 (b2 f  a2 y )  p(b1 f  a1 y )  b0 f  a0 y.
(8.7)
y

1 b2
a
1 b
{ f  2 y [ 1 f 
p a3
a3
p a3
a
a1
1 b
y  ( 0 f  0 y )]}.
a3
p a3
a3
(8.8)
В соответствии с методом последовательного интегрирования,
уравнению (8.8) соответствует следующая система дифференциальный
уравнений в форме Коши:




y  y3 ,


y  y2 , 



y3 
b0
a
f  0 y,
a3
a3
y 2 
b1
a
f  1
a3
a3
y1 
b2
a
f  2
a3
a3
y  y1.
Пусть методом
уравнение вида:
Эйлера
необходимо
(8.9)
решить
y  F ( y ),
y
 F ( y ),
t
h  t  шаг интегрирования,
yk 1  yk  y  hF ( y ),
yk 1  yk  hF ( y ).
На основе (8.9) окончательно можно записать:
дифференциальное



b
a

y2  y2  h( 1 f  1 y  y3 ), 
a3
a3


b2
a2
y1  y1  h( f  y  y2 ), 
a3
a3


y  y1.

y3  y3  h (
b0
a
f  0 y ),
a3
a3
(8.10)
Условием завершения расчета является проверка неравенства вида:
ymin  x1C
x1C

0,05
;
2
ymin  x  0,025  x .
C
1
C
1
(8.11)
Шаг интегрирования рассчитывается по формуле:
h
1)
2)
3)
4)
a1
.
40a0
(8.12)
Таким образом, основными этапами расчета являются:
Организовать ввод в диалоге с пользователем исходных параметров.
Расчет a k и b j .
Расчет h .
Расчет f   Z 0 .
Обнуление переменных y, y1 , y2 , y3 .
5)
6) t  0 .
7) Цикл
 расчет по формуле (8.10);
 организация вывода результата с контролем окончания цикла;
Конец цикла.
8.4 Устойчивость систем со звеном чистого запаздывания
1) Уравнение процессов в звене (см. рисунок 8.3):
y  V (t   ).
(8.17)
V
y
1(t )
1(t   )
1
1
t
t

Рисунок 8.3 –Графики функций
2) Передаточная функция звена
W ( p)  e p ,
(8.18)
где   const - величина чистого запаздывания.
3) Частотная передаточная функция
W ( j )  e  j  A( )e  j ( ) ,
(8.19)
A( )  1,
 ( )  1.
(8.20)
Пусть дана структурная схема исходной системы (см. рисунок 8.4).
V ( p)
k РС
T1 p  1
1
T2 p  1
ep
()
Рисунок 8.4 – Схема исходной системы
Y ( p)
Пусть:
k РС  100;
T1  T2  0.1c;
  0.01c;
L0  20 lg k РС  40дБл;
c  10c 1 ;
lg c  1.

L ( ) дБ
40
20
1
2
3
lg()
-90
-180
-270
Рисунок 8.5 – Логарифмические амплитудочастотная и фазочастотная
характеристики
5 Синтез систем
Под синтезом системы понимается такое построение системы, при
котором переходный процесс удовлетворяет заданным значениям показателям
качества функции системы.
9.1 Оценка качества переходного процесса в системе
Переходные процессы, возникающие в системе при скачкообразном
процессе принято делить на группы (см. рисунок 9.1 а, б).
Рисунок 9.1 –Примеры переходных процессов в устойчивой системе
На рисунке 9.1 введены следующие обозначения:
1 – апериодический переходный процесс, в котором
изменяет знак;
2 – монотонный переходный процесс, у которого
3 – колебательный переходный процесс;

y

y
один раз
не изменяет знака;
y 0 – требуемое установившееся значение выходной координаты
системы.
Оценка качества переходного процесса при скачкообразном входном
воздействии осуществляется по следующим показателям:
1) t p
– это такое минимальное время, после которого выходная
регулируемая координата системы соответствует условию:
ymax  y0

y0
(9.1)
где  – допустимое отклонение выходной координаты от заданного значения
y 0 , где y 0
2)
= 0,05 (5%);
–
перерегулирование – это максимальное отклонение выходной
координаты от установившегося значения, рассчитанная в процентах,
при этом расчетная формула:
y1max  y0

100%
y0
3) Вид переходного процесса (колебательный или монотонный);
4) Частота собственных колебаний (и период);
1
f

5) k T
k
(Гц);
(9.2)
6) Количество колебаний.
9.2 Метод параметрического синтеза
При этом структура корректирующего устройства считается заданной. В
результате синтеза определяется передаточная функция и параметры
корректирующего устройства.
9.3 Метод синтеза систем на основе логарифмических амплитудо –
частотных характеристик
При этом на основе заданных значений показателей качества переходного
процесса определяется структура и параметры корректирующего устройства.
На рисунке 9.2 приведена структурная схема скорректированной системы.
Исходная нескорректированная система
V(p)
Wky ( p )
W1 ( p )
W2 ( p )
Y(p)
W3 ( p )
Рисунок 9.2 –Структурная схема скорректированной системы
Передаточная функция исходной нескорректированной
разомкнутом состоянии, определяется по формуле:
Wpcн (p)  W1 ( p) W2 ( p) W3 ( p)
Процессы в скорректированной
желаемым, поэтому можно записать:
системе
должны
системы
в
(9.3)
соответствовать
W pccк (p)  Wку ( p ) W pcн ( p )  W pcж ( p ),
(9.4)
ж
где W pc ( p ) – передаточная функция желаемой системы;
Wку ( p) – передаточная функция корректирующего устройства.
Тогда передаточная функция корректирующего устройства может быть
рассчитана так:
W pcж ( p )
Wку ( p )  н
(9.5)
W pc ( p )
При p  j на основе (9.5) можно записать частотную передаточную
функцию корректирующего устройства:
Wку ( j ) 
W pcж ( j )
W pcн ( j )
Тогда окончательно можно записать:
(9.6)
Aку ( ) 
ж
Apc
( )
н
Apc
( )
,
ж
н
20 lg Aку ( )  20 lg Apc
( )  20 lg Apc
( ),
Lку ( )  Lжpc ( )  Lнpc ( ).
(9.7)
Желаемой называют такую ЛАЧХ скорректированной системы, при
которой в системе обеспечивается требуемый переходный процесс.
Основные требования к переходному процессу:
- время регулирования t p не должно превышать некоторого заданного
значения t 0 , то есть, t p  t 0 ;
-
перерегулирование
допустимого значения

так же не должно превышать некоторого
 0 , то есть    0 .
По соответствующим номограммам [1-3] на основе t 0 и
 0 определяются
ж
параметры L pc ( ) .
Пусть на рисунке 9.3 построена структурная схема.
W pcH ( p )
V(p)
Wky ( p )
K Tpc
T1 p  1
1
T2 p  1
1
T3 p  1
Y(p)
Рисунок 9.3 – Структурная схема системы
Пусть звенья исходной нескорректированной системы имеют следующие
параметры:
K Tpc  40; T1  1c; T2  0.5c; T3  0.05c.
ж
Пусть в соответствии с заданными требованиями для L pc ( ) определены
[1-3] следующие величины:
cp  4c 1; lg( c )  0.6;
Lmax   Lmin  12дБ ;
L0  20lg K Tpc  20 lg 40  20  1.6  32дБ ;
c 
1
 1c 1 ; lg(  c1 )  0;
T1
c 
1
 2c 1 ; lg(  c2 )  0.3;
T2
c 
1
 20c 1 ; lg(  c4 )  1.3;
T3
1
2
3

L( ) дБ
 40дБ/дек
40
LНpc
Lжpc
32
20
 20дБ/дек
12
-1
-0.5
0
1
 2 3
lg()
1
4
2
-12
-20
Lky()
Рисунок 9.4 –Логарифмические амплитудочастотные характиристики
Анализ Lку ( ) позволяет записать передаточную функцию корректирующего
устройства:
(T2ку p  1) 2 (T3 p  1)
Wку ( p)  ку
;
(T1 p  1) 2 (T4 p  1)
T jку 
j
;
1
1
 1.4c; T2ку   1c;
0.7
1
1 1
1
1

  0.5c; T4ку 

 0.05c.
3 2
4 20
T1ку 
T3ку
1
10 Основы автоматизированного управления
Управление – это процесс целенаправленного воздействия на объект, при
котором обеспечивается его эффективное функционирование.
Автоматизированная система управления (АСУ) – человеко–машинная
система, использующая на базе вычислительной техники (ВТ) совокупность
кибернетических, экономико – математических и организационных моделей и
направленная на эффективное функционирование объекта.
10.1 Структуризация систем
Под структуризацией понимается процесс деления
«обозримые» части и фиксирования связей между ними.
Структуризацию проводят по признакам:
1) функциональный (см. рисунок 10.1)
системы
на
АСУ
Функциональная
часть
P1Ф
  
Обеспечивающая
часть
PnФ
P1o
  
Pmo
Рисунок 10.1 –Схема системы
На рисунке введены следующие обозначения:
ф
i
p , p oj – функциональная и обеспечивающая подсистемы соответственно,
j  1, m; i  1, n.
Функциональная часть – комплекс автоматизируемых функций и задач,
представляющих содержательную сторону уравнения.
Обеспечивающая часть – совокупность условий, являющихся
необходимыми для функционирования системы в автоматизированном
режиме.
3) деление процесса управления на фазы (см. рисунок 10.2).
Директивная
информация из
надсистемы
Прогнози
рование
В надсистему
Контроль
Нормиро
вание
Анализ
Планиро
вание
Учет
Регулирование
ОУ
Рисунок 10.2 –Схема взаимосвязи фаз управления
На рисунке 10.3 приведена обобщенная схема контура управления
Z
V
Блок
ОП
V
Механизм
управления
Y
ОУ
Рисунок 10.3 –Схема контура управления
Подробное рассмотрение вопросов проектирование систем
автоматизированного управления приведено в учебном пособии автора [4].
Список литературы
1 Востриков А.С. Теория автоматического регулирования: учебное пособие /
А.С. Востриков, Г.А. Французова.- Новосибирск: Изд-во НГТУ, 2006.-368 с.
2 Попов Е.П. Теория линейных систем автоматического управления и
регулирования: учебник / Е.П. Попов.-М.: Наука, 1989.-300 с.
3 Воронов А.А. Основы теории автоматического управления/ А.А. Воронов.М.: Энергия,1980.-320 с.
4 Раздобреев М.М. Проектирование систем автоматизированного
управления: учебное пособие / М.М. Раздобреев. – Новосибирск, Изд – во
НЭТИ, 1989.- 80с.