9. звуковое поле на оси круглого поршневого излучателя

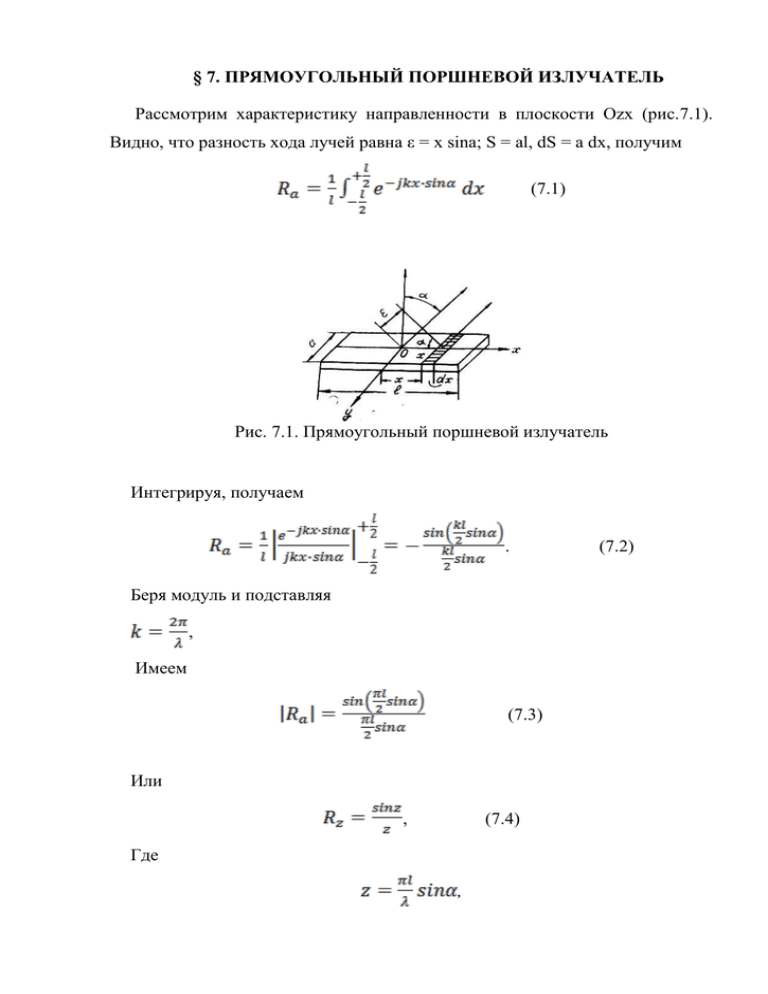
§ 7. ПРЯМОУГОЛЬНЫЙ ПОРШНЕВОЙ ИЗЛУЧАТЕЛЬ
Рассмотрим характеристику направленности в плоскости Ozx (рис.7.1).
Видно, что разность хода лучей равна ε = х sina; S = al, dS = a dx, получим
(7.1)
Рис. 7.1. Прямоугольный поршневой излучатель
Интегрируя, получаем
.
Беря модуль и подставляя
,
Имеем
(7.3)
Или
,
(7.4)
Где
,
(7.2)
График Rа, построенный в декартовых координатах по (7.4), изображен на
рис. 7.2. Определяя из этого графика величины отношения первых трех
дополнительных максимумов A1, A2, A3 к основному максимуму A0, получим
Для заданных размеров излучателя
.
(7.5)
Угол θ раствора главного максимума найдем, положив в Ra = 0. Тогда
.
Рис. 7.2. Характеристика направленности прямоугольного поршневого
излучателя
Как видно из (7.5), острота направленного
излучателя зависит от отношения
λ/l.
действия
прямоугольного
Чем меньше его величина, тем
меньше угол θ, определяющий остроту направленного действия.
Острота максимума прямоугольной системы находится по формуле
.
(7.6)
Полагая ν =0,1, получаем
.
(7.7)
§ 8. ОСЦИЛЛИРУЮЩАЯ СФЕРА
Под осциллирующей сферой понимается жесткая сфера, центр которой
совершает осевые, или аксиальные, колебания (рис. 8.1). Рассмотрим
особенности акустического поля создаваемого осциллирующей сферой.
Предположим, что сфера колеблется вдоль оси x по гармоническому закону.
Распределение нормальных составляющих колебательной скорости по
поверхности сферы, колеблющейся вдоль оси х со скоростью ξ' = ξ ’aejwt
должно следовать зависимости
,
(8.1)
где ξ’r радиальная колебательная скорость точек на поверхности сферы.
Рис. 8.1. Осциллирующая сфера
Ясно, что при совершении сферой осевых колебаний в упругой среде
знаки давлений, возникающих на передней и задней сторонах поверхности
сферы, будут различными. Например, когда движение сферы происходит в
положительном направлении оси х, на передней стороне поверхности сферы
возникает сжатие, в то время как позади сферы будет формироваться зона
разрежения. При изменении направления движения области сжатия и
разрежения переменятся местами. Как видно, осциллирующая сфера должна
обладать дипольным действием.
Примем в дальнейшем, что размеры сферы малы по сравнению с длиной
волны. Оставаясь в рамках этого допущения, будем считать, что потенциал
скорости в акустическом поле осциллирующей сферы может быть с хорошим
приближением описан выражением. Определим постоянную А', входящую в
это выражение.
Постоянная А' может быть определена из пограничного условия, согласно
которому радиальная скорость ξ’r = ξ’а cos α еjωt в каждой точке на
поверхности сферы должна равняться радиальной компоненте скорости в
акустическом поле при r = R (R — радиус сферы). Так как размеры сферы
малы по сравнению с длиной волны, то выражение для потенциала скорости
на поверхности сферы может быть взято в следующем упрощенном виде:
.
(8.2)
Выражение (62) следует из общего выражения для потенциала диполя,
если в нем положить:
;
;
Рис. 8.2.
Распределение радиальных составляющих колебательной
скорости по поверхности осциллирующей сферы
Определяя радиальную колебательную скорость дифференцированием
(8.2) по R, находим
.
(8.3)
С другой стороны, согласно пограничному условию (8.1)
.
Сопоставляя (8.1) и (8.3), определяем
.
(8.4)
Подставив значение А' из (8.4) в (8.2), находим потенциал скорости на
поверхности сферы
.
(8.5)
Давление на поверхности осциллирующей сферы в свою очередь
определяется как
.
(8.6)
Модуль pr=R равен
.
(8.7)
Вычислим теперь давление и интенсивность в дальнем акустическом поле,
создаваемом осциллирующей сферой.
Полагая kr >>1, исходим из точного выражения для потенциала скорости
диполя:
,
в котором теперь надо считать
При
приближенно можно принять
.
Для модуля давления при этом
получим
(8.8)
,
(8.9)
где
- объем сферы.
Для интенсивности соответственно получаем
вт
/см2
(8.10)
Как явствует из (8.10), с увеличением частоты (при поддержании ξа'=
const) интенсивность Ja,r резко возрастает. Зная интенсивность Ja,r, можно
определить
акустическую
мощность
и
сопротивление
излучения
осциллирующей сферы. Окружим сферу поверхностью S волнового фронта
радиуса г. Элементарная мощность, приходящаяся на элементарный шаровой
пояс dS, равна
.
(8.11)
Интегрируя (8.11) по углу α в пределах от 0 до π, найдем полную
акустическую мощность сферы (рис. 8.3):
.
Так как
то
вт
/см2
(8.12)
С другой стороны, мощность Ра определяется по общей формуле:
вт.
(*)
Рис. 8.3. К определению акустической мощности и сопротивления излучения осциллирующей сферы
Сопоставляя правые части (8.12) и (*), определяем сопротивление
излучения:
.
(8.13)
Если в (8.13) положить Vсф = (4/3)πR3,то выражение (8.13) может быть
также представлено в виде
(8.14)
Рассмотрение поля, создаваемого осциллирующей сферой было проведено
нами в предположении малости размеров сферы по сравнению с длиной
волны (т. е. при
).
Более строгая теория, справедливая при любых kR, дает следующее
выражение для комплексного сопротивлении излучения осциллирующей
сферы:
(8.15)
Вещественная часть этого выражения представляет собой активное
сопротивление излучения, а мнимая часть— произведение соколеблющейся
массы на круговую частоту ω:
(8.16)
(8.17)
В случае если размеры осциллирующей сферы невелики по сравнению с
длиной волны, выражение (8.15) упрощается, принимая вид
(8.18)
Сопротивление излучения RS и соколеблющуюся массу Ms в этом случае
определяют выражения:
;
(8.19)
.
(8.20)
Формула (8.19) совпадает с формулой (8.14), полученной выше для
осциллирующей сферы, малой в сравнении с длиной волны.
Из
(8.20)
следует,
что
соколеблющаяся
масса
осциллирующей
сферы на низких частотах равна половине массы среды в объеме
сферы. На высоких частотах (при
)
.
Соколеблющаяся
масса
на
высоких
(8.21)
частотах
при
возрастании
kR убывает, стремясь к нулю:
.
(8.22)
Осциллирующая сфера как излучатель звука оказывается значительно
менее эффективной, чем пульсирующая сфера. Дело в том, что
осциллирующая сфера при низких частотах является излучателем,
работающим в режиме короткого акустического замыкания. На передней
стороне осциллирующей сферы среда оказывается сжатой, а на задней
стороне — разреженной. При медленных колебаниях, характерных для
низких частот, существует возможность выравнивания давления между
передней и задней сторонами сферы. Следует иметь в виду, что
интенсивность звука, создаваемая осциллирующей сферой, в общем случае
выражается так:
.
(8.23)
Эта формула отлична от обычной формулы, согласно которой
Рис. 8.4. Характеристика направленности осциллирующей сферы
Очевидно, только при
, т. е. в дальнем акустическом поле, для
вычисления интенсивности поля осциллирующей сферы можно пользоваться
формулой
В отличие от пульсирующей сферы осциллирующая сфера обладает
направленным действием. Характеристика направленности осциллирующей
сферы имеет форму восьмерки (рис. 8.4). Максимум излучения получается
вдоль оси осциллирования.
§ 9. ЗВУКОВОЕ ПОЛЕ НА ОСИ КРУГЛОГО ПОРШНЕВОГО
ИЗЛУЧАТЕЛЯ
Применим формулу Рэлея для вычисления давления в точках на оси
круглого поршня, который предполагается заделанным в экране
безграничных размеров (рис. 9.1). Выберем в качестве излучающего элемента
dS «поверхности поршня элементарное кольцо радиуса ρ. Имеем
,
поскольку
.
На основании формулы Рэлея
.
(9.1)
Интегрируя, находим:
(9.2)
или
(9.3)
Рис. 9.1. Круглый поршень в экране безграничных размеров
Для модуля давления имеем
(9.4)
Подставляя
,
окончательно получаем
(9.5)
Если в (9.5) положить
,
то получим давление в центре поршня
.
(9.6)