Тема 8: Теория выбора в условиях неопределенности Лекция 2

Тема 8: Теория выбора в условиях неопределенности
Лекция 2.
Теория ожидаемой полезности
Мы можем задать предпочтения индивида на множестве лотерей.
При некоторых условиях (в этом курсе они не обсуждаются), предпочтения индивида на
множестве простых лотерей можно представить функцией ожидаемой полезности следующего
вида:
U(L) =
p
S
v( x S ) , где
s
- ps – вероятность состояния мира s,
- xs – доход потребителя в состоянии мира s
- v(.) – элементарная, или Бернуллевская функция полезности.
Функцию U(.) также
Моргенштерна.
называют
функцией
ожидаемой
полезности
фон
Неймана-
Функция ожидаемой полезности единственна с точностью до аффинного преобразования, то
есть:
Если U(.) – функция ожидаемой полезности, отражающая некоторые предпочтения, то
~
U (.) = a + bU(.), a ≥ 0, b > 0 отражает те же предпочтения.
ПРИМЕР: Вася Пупкин устраивается на работу страховым агентом. Ему предлагают две
возможных схемы вознаграждения: постоянная зарплата в $900, или комиссионные от
продаж. Возможны два равновероятных варианта развития событий:
- бум на рынке страховых услуг  комиссионные составят $6400
- стагнация  комиссионные составят $400, с равной вероятностью.
? Какую схему выберет Вася, если его элементарная функция полезности v( x) 
x?
Фактически, речь идет о выборе между двумя лотереями: L2 = {(6400; 400) (1/2; 1/2)} и
L1 = {(900),(1)}, которые мы можем сравнить с помощью Васиной функции ожидаемой
полезности:
U ( L2 ) 
1
1
6400 
400  U ( L1 )  1 900
2
2
1
1
80  20  30
2
2
50  30
 Вася выберет комиссионные.
Проблемы теории ожидаемой полезности:
Теория ожидаемой полезности относительно проста и универсальна – и, как многие простые и
универсальные теории, она время от времени противоречит поведению реальных экономических
агентов.
Одно из наиболее известных противоречий носит имя парадокса Алле*
* Морис Алле, французский экономист XX в., Нобелевский лауреат
1 of 4
М. Алле провел следующий эксперимент:
Потребителю предлагался выбор между двумя лотереями:
L1 = {(2,5; 0,5; 0), (0; 1; 0)}
L2 = {(2,5; 0,5; 0), (0,1; 0,89; 0,01)}
Для большинства потребителей, L1  L2
Затем тому же потребителю предлагался выбор между:
L3 = {(2,5; 0,5; 0), (0; 0,11; 0,89)}
L4 = {(2,5; 0,5; 0), (0,1; 0; 0,9)}
Большинство потребителей предпочитало L4  L3
?
Почему такой выбор противоречит теории ожидаемой полезности?
Пусть предпочтения потребителя представимы функцией ожидаемой полезности. Тогда
L1  L2 и L4  L3 только тогда, когда:
v(0,5)  0,1v(2,5)  0,89v(0,5)  0,01v(0)

0,1v(2,5)  0,9v(0)  0,11v(0,5)  0,89v(0)
Сложив два уравнения этой системы, получим:
0,1v(2,5)  0,9v(0)  v(0,5)  0,1v(2,5)  v(0,5)  0,9v(0)  0,1v(2,5)  0,1v(2,5)  невозможно.
Возможные объяснения парадокса Алле:
- Люди недооценивают малые вероятности и переоценивают большие
- Люди относятся к проигрышам и выигрышам асимметрично
Денежные лотереи и отношение к риску.
Пусть L – некоторая нетривиальная лотерея, E(L) – математическое ожидание выигрыша в
лотерее L, U(.) – функция ожидаемой полезности. В этом случае:
Индивид является рискофобом, если L, U(L) < U(E(L))
Индивид является рискофилом, если L, U(L) > U(E(L))
Индивид является нейтральным к риску, если L, U(L) = U(E(L))
Заметим, что вышеуказанные неравенства можно переписать в ином виде. Например,
определение рискофобии можно переформулировать так:

 p v( x )  v  p x
s
s
s
s
s
s



- это неравенство служит определением вогнутости функции v(.).
Это позволяет нам судить об отношении к риску на основании свойств элементарной функции
полезности:
Индивид является рискофобом, если v(.) является строго вогнутой
Индивид является рискофилом, если v(.) является строго выпуклой
Индивид является нейтральным к риску, если v(.) линейна
Введем понятие денежного эквивалента лотереи:
Будем называть денежным эквивалентом (certainty equivalent, CE(L)) лотереи L такую сумму
денег m, полученную с определенностью, что:
U(L) = U(m)
2 of 4
Ведем понятие премии за риск:
Для лотереи L, будем называть премией за риск (risk premium, RP(L)), разность:
E(L) - CE(L)
Графическая иллюстрация отношения к риску с помощью элементарной функции
полезности
Рассмотрим лотерею L = {(x1, x2), (p, 1 – p)}, x1 > x2. Предположим, элементарная функция
полезности потребителя – v(x).
Рассмотрим три варианта отношения к риску:
Случай 1: потребитель – рискофоб, v”(x) < 0
Exp. Utility
v(x)
U(E(L)
Денежный
эквивалент лотереи
U(L)
Будем называть денежным эквивалентом лотереи L такой
Примеры
положительная премия за риск
x1 CE(L) E(L)
x2
x
Случай 2: потребитель – рискофил, v”(x) > 0
Exp. Utility
v(x)
Денежный эквивалент лотереи
U(L) называть денежным эквивалентом лотереи L такой
Будем
отрицательная премия за риск
U(E(L))
Примеры
x1
E(L) CE(L) x2
x
Случай 3: потребитель – риск-нейтрал, v”(x) = 0
Exp. Utility
v(x)
Денежный эквивалент лотереи
U(L) =называть
U(E(L)) денежным эквивалентом лотереи L такой
Будем
Примеры
x1 E(L)=CE(L)
x2
x
3 of 4
!
Заметим, что величины денежного эквивалента лотереи и премии за риск зависят от
первоначального богатства индивида!
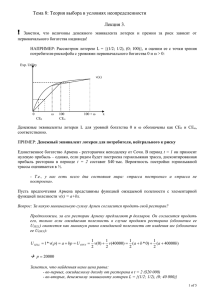
НАПРИМЕР: Рассмотрим лотерею L = {(1/2; 1/2), (0; 100)}, и оценим ее с точки зрения
потребителя-рискофоба с уровнями первоначального богатства 0 и ω > 0:
Exp. Utility
v(x)
Денежный эквивалент лотереи
Будем называть денежным эквивалентом лотереи
Примеры
ω
0
CE0
100
CE
100 + ω
x
Денежные эквиваленты лотереи L для уровней богатства 0 и ω обозначены как CE0 и CEω,
соответственно.
ПРИМЕР:
Единственное богатство Армена - ресторанчик неподалеку от Сочи. В период t = 1 он приносит
нулевую прибыль – однако, если рядом будет построена горнолыжная трасса, дисконтированная
прибыль ресторана в периоде t = 2 составит $40 тыс. Вероятность постройки горнолыжной
трассы оценивается в ½.
- Т.е., у нас есть всего два состояния мира: «трасса построена» и «трасса не
построена».
Пусть предпочтения Армена представимы функцией ожидаемой полезности с элементарной
функцией полезности v(x) = a+bx.
Вопрос: За какую минимальную сумму Армен согласится продать свой ресторан?
Предположим, за его ресторан Армену предлагают p долларов. Он согласится продать
его, только если ожидаемая полезность в случае продажи ресторана (обозначим ее
USELL) окажется как минимум равна ожидаемой полезности от владения им (обозначим
ее UOWN):
U SELL  1 * v( p)  a  bp  U OW N 
1
1
1
1
v(0)  v(40000)  (a  b * 0)  (a  40000b)
2
2
2
2
 p  20000
Заметим, что найденная нами цена равна:
- во-первых, ожидаемому доходу от ресторана в t = 2 ($20 000)
- во-вторых, денежному эквиваленту лотереи L = {(1/2; 1/2), (0; 40 000)}
4 of 4