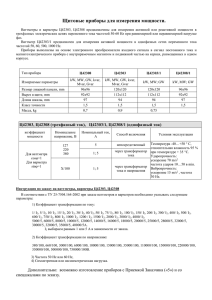
Физика: часть 1

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
ГОУ ВПО «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ
ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
В. В. Алексеев, В. Г. Приданов
ФИЗИКА
Часть 1
учебно-методический комплекс для студентов ОЗО
факультета технологии и предпринимательства НГПУ
Новосибирск
2009
1
УДК 53 (075.8)
ББК 22.3я 73–1
А 471
Печатается по решению
Редакционно-издательского совета НГПУ
Р е ц е н з е н т ы:
доктор физико-математических наук, профессор,
заведующий кафедрой общей и теоретической физики НГПУ
Ю. Э. Овчинников;
кандидат технических наук, профессор,
заведующий кафедрой машиноведения НГПУ
В. М. Потапов;
доктор физико-математических наук,
профессор кафедры общей физики НГТУ
Ю. Г. Пейсахович
Алексеев, В. В.
А 471
Физика: учебно-методический комплекс для студентов ОЗО факультета технологии предпринимательства/ В. В. Алексеев, В. Г. Приданов. –
Новосибирск: Изд. НГПУ, 2009. – 220 с.
Учебно-методический комплекс составлен в соответствии с требованиями
Государственного образовательного стандарта высшего профессионального образования по специальностям: 030600 «Технология и предпринимательство»;
230700 «Сервис»; 030500.08 «Профессиональное обучение». Содержит полный
объем материалов для самостоятельного освоения курса физики по трем разделам: «Механика», «Молекулярная физика», «Электричество и магнетизм», расширенный анализ решения физических задач; перечень тестовых заданий для
проверки знаний, вопросов к экзамену, варианты контрольных работ, а также список рекомендуемой литературы.
Адресован студентам заочной формы обучения факультета технологии и
предпринимательства.
УДК 53 (075.8)
ББК 22.3я 73–1
© Алексеев В. В., Приданов В. Г., 2009
© ГОУ ВПО «Новосибирский государственный
педагогический университет», 2009
2
СОДЕРЖАНИЕ
I. Рабочая программа учебной дисциплины «Физика» ....................... 7
1.1. Выписка из образовательного стандарта
по учебной дисциплине .................................................................... 7
1.2. Цели, задачи и роль дисциплины
в системе профессиональной подготовки ..................................... 7
1.3. Принципы построения учебно-методического комплекса ............ 7
2. Содержание дисциплины ....................................................................... 8
2.1. Тематический план
8
2.2. Содержание отдельных тем учебных дисциплин ....................... 9
3. Информационное обеспечение учебной дисциплины ...................... 10
3.1. Вопросы к экзамену ..................................................................... 10
3.2. Варианты контрольных работ ..................................................... 12
3.3. Список рекомендуемой литературы .......................................... 14
II. Методические рекомендации по изучению дисциплины ............. 15
III. Теоретический материал по дисциплине «Физика» .................... 17
1. Механика .............................................................................................. 17
1.1. Кинематика .................................................................................... 17
1.1.1. Механическое движение ....................................................................... 17
1.1.2. Скорость ................................................................................................ 18
1.1.3. Ускорение .............................................................................................. 20
1.1.4. Угловая скорость и угловое ускорение ................................................ 21
1.1.5. Нормальное и тангенциальное ускорения............................................ 23
1.2. Законы Ньютона ............................................................................ 26
1.2.1. Сила. Упругие силы и силы трения ...................................................... 26
1.2.2. Первый закон Ньютона ...................................................................... 28
1.2.3. Второй закон Ньютона ....................................................................... 29
1.2.4. Третий закон Ньютона........................................................................ 33
1.2.5. Закон всемирного тяготения .............................................................. 33
1.2.6. Движение тел относительно инерциальных и неинерциальных
систем отсчета ............................................................................................ 36
1.3. Основные законы сохранения ..................................................... 39
1.3.1. Закон сохранения импульса ............................................................... 39
1.3.2. Физические понятия вращательного движения ............................... 43
3
1.3.3. Закон сохранения полной механической энергии ........................... 50
1.3.4. Основное уравнение динамики вращательного движения ............. 52
1.3.5. Закон сохранения момента импульса ............................................... 54
1.4. Колебательное движение............................................................. 56
1.4.1. Гармонические колебания .................................................................. 56
1.4.2. Затухающие колебания ....................................................................... 61
1.4.3. Вынужденные колебания ................................................................... 63
1.5. Движение жидкостей и газов ...................................................... 65
1.5.1. Линии и трубки тока. Уравнение неразрывности ............................ 65
несжимаемой струи ................................................................................... 65
1.5.2. Уравнение Бернулли ............................................................................. 67
1.5.3. Вязкое трение ...................................................................................... 69
1.5.4. Ламинарное и турбулентное течения ................................................ 71
1.5.5. Течение Пуазейля ................................................................................ 72
1.6. Основы механики упругих тел ................................................... 75
1.6.1. Упругие и пластические деформации ............................................... 75
1.6.2. Закон Гука ............................................................................................ 77
1.6.3. Диаграмма деформирования .............................................................. 79
1.6.4. Потенциальная энергия деформации ................................................ 80
1.6.5. Деформация сдвига ............................................................................. 80
2. Молекулярная физика ....................................................................... 83
2.1. Молекулярно-кинетическая теория газов..................................... 83
2.1.1. Основные понятия................................................................................. 83
2.1.2. Модель идеального газа ..................................................................... 85
2.1.3. Уравнение Клапейрона–Менделеева ................................................ 86
2.1.4. Основное уравнение молекулярно-кинетической теории .............. 88
2.1.5. Распределение Максвелла .................................................................. 90
2.1.6. Барометрическая формула ................................................................. 92
2.2. Основы термодинамики............................................................... 93
2.2.1. Внутренняя энергия. Первое начало термодинамики ..................... 93
2.2.2. Теплоемкость ....................................................................................... 95
2.2.3. Равновесные процессы ....................................................................... 97
2.2.4. Изопроцессы ........................................................................................ 98
2.2.5. Второе начало термодинамики ........................................................ 101
2.2.6. Тепловые машины. Цикл Карно ...................................................... 106
2.3. Агрегатные состояния вещества ................................................. 108
4
2.3.1. Ван-дер-ваальсовский газ ................................................................... 108
2.3.2. Критическое состояние ....................................................................... 111
2.3.3. Изотермы Ван-дер-Ваальса ................................................................ 112
2.4. Физическая кинетика ................................................................. 113
2.4.1. Диффузия ........................................................................................... 114
2.4.2. Теплопроводность ............................................................................. 115
2.4.3. Вязкое трение .................................................................................... 116
2.4.4. Длина свободного пробега молекул ................................................ 117
3. Электричество и магнетизм ........................................................... 122
3.1. Электрическое поле ................................................................... 122
3.1.1. Электрический заряд ........................................................................ 122
3.1.2. Закон Кулона ..................................................................................... 122
3.1.3. Напряженность электрического поля................................................. 123
3.1.4. Принцип суперпозиции .................................................................... 125
3.1.5. Линии напряженности ...................................................................... 127
3.1.6. Поток вектора. Теорема Гаусса .......................................................... 128
3.1.7. Применение теоремы Гаусса для расчета электрических полей . 129
3.1.8. Работа сил электрического поля ...................................................... 132
3.1.9. Потенциал .......................................................................................... 133
3.2. Диэлектрики и проводники в электрическом поле ................ 136
3.2.1. Диэлектрики....................................................................................... 136
3.2.2. Диполь в электрическом поле и диэлектрике ................................ 138
3.2.3. Сегнетоэлектрики. Пьезоэлектрический эффект ........................... 140
3.2.4. Проводники в электрическом поле ................................................. 142
3.2.5. Электроемкость. Конденсаторы ...................................................... 142
3.3. Постоянный электрический ток ............................................... 147
3.3.1. Сила тока ............................................................................................ 147
3.3.2. Электродвижущая сила. Напряжение ............................................. 148
3.3.3. Закон Ома для однородного участка цепи ..................................... 149
3.3.4. Закон Джоуля–Ленца. Закон Ома для неоднородного участка .. 151
3.3.5. Правила Кирхгофа ............................................................................ 153
3.3.6. Расчет мощности, выделяемой в цепи ............................................ 156
3.3.7. Электрический ток в различных средах ......................................... 158
3.3.8. Термоэлектронные явления ............................................................. 163
3.4. Магнитное поле в вакууме и веществе .................................... 165
3.4.1. Характеристики магнитного поля ................................................... 165
5
3.4.2. Закон Био–Савара–Лапласа.............................................................. 166
3.4.3. Намагничивание вещества ............................................................... 172
3.4.4. Закон Ампера ..................................................................................... 174
3.4.5. Работа по перемещению проводника с током в магнитном поле 177
3.4.6. Сила Лоренца ..................................................................................... 178
3.5. Электромагнитная индукция .................................................... 181
3.5.1. Опыты М. Фарадея. Закон Фарадея ................................................ 181
3.5.2. Токи Фуко .......................................................................................... 184
3.5.3. Явление самоиндукции ....................................................................... 185
3.5.4. Токи при размыкании и замыкании цепи........................................... 187
3.5.5. Индуктивность .................................................................................. 188
3.5.6. Энергия магнитного поля ................................................................. 189
3.5.7. Взаимная индукция ........................................................................... 190
3.5.8. Переменный ток ................................................................................ 192
3.5.9. Электрические цепи с изменяющимся током ................................ 197
IV. Комбинированные тесты по физике .............................................. 201
Приложение ................................................................................................ 220
6
I. РАБОЧАЯ ПРОГРАММА
УЧЕБНОЙ ДИСЦИПЛИНЫ «ФИЗИКА»
1.1. Выписка из образовательного стандарта по учебной дисциплине
Физические основы механики. Понятие состояния в классической механике.
Уравнения движения, законы сохранения, принцип относительности в механике.
Кинематика и динамика твердого тела, жидкостей и газов. Статическая и молекулярная физика и термодинамика: три начала термодинамики, термодинамические
функции состояния, фазовые равновесия и фазовые превращения, элементы
неравновесной термодинамики, кинематические явления. Физический практикум.
Электричество и магнетизм. Электростатика и магнитостатика в вакууме и веществе. Квазистационарные токи. Физика колебаний и волн. Принцип относительности в электродинамике.
1.2. Цели, задачи и роль дисциплины в системе профессиональной
подготовки
Цель курса: сформировать у студентов логичную систему представлений об основных концепциях и фундаментальных законах современной физики. Представить
физику как основу современного естествознания.
Задачи курса:
 расширить и углубить знания, полученные студентами в школьном курсе физики, для построения замкнутой системы основных физических законов;
 раскрыть физические методы исследования и сформировать представление о
физике как науке, имеющей экспериментальную основу;
 научить грамотной постановке и проведению физического эксперимента;
 развить самостоятельность и активность мышления путем решения конкретных
физических задач.
 подготовить к освоению элементов предметной подготовки для инженерных
специальностей, фундаментом которых является физика.
Место курса в системе подготовки специалиста. Данный курс является, в соответствии с государственным образовательным стандартом, обязательной частью
подготовки студентов на факультете технологии и предпринимательства. Содержание
курса содействует расширению знаний о закономерностях реальных процессов, протекающих в природе, понимание которых на современном уровне является необходимым для будущего педагога, и организовано с учетом опыта преподавания физики на
факультете технологии и предпринимательства студентам заочной формы обучения.
1.3. Принципы построения учебно-методического комплекса
Учебно-методический комплекс составлен в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования
7
по специальностям: 030600 «Технология и предпринимательство»; 230700 «Сервис»;
030500.08 «Профессиональное обучение».
В основу настоящего учебно-методического комплекса положены материалы
учебного пособия для студентов высших учебных заведений В. Г. Приданова «Краткий курс лекций по общей физике»: ч. 1.«Механика. Молекулярная физика и введение
в термодинамику»; ч. 2. «Электричество и магнетизм. Оптика» (Новосибирск: изд.
НГПУ, 2005), учебно-методического комплекса для студентов I курса факультета технологии и предпринимательства «Физические основы технической механики» (Новосибирск: изд. НГПУ, 2007), а также учебной программы по курсу общей физики, составленной Л. А. Борыняком, Г. Ф. Сивых (Новосибирск: изд. НГПУ, 2001).
2. Содержание дисциплины
2.1. Тематический план
Тема
Лекции
(ч.)
Семинары, практ.
занятия (ч.)
Самостоятельная
работа (ч.)
1. Кинематика материальной точки.
Виды движения. Кинематические характеристики.
1
2
4
2. Динамика материальной точки,
твердого тела. Законы Ньютона. Динамические характеристики вращательного движения твердого тела.
2
2
8
3. Основные законы сохранения.
Движение жидкостей и газов.
2
2
8
4. Основы механики упругих тел.
1
2
4
5. Молекулярно-кинематическая теория газов.
2
2
8
6. Основы термодинамики.
2
2
8
7. Агрегатные состояния вещества.
1
2
4
8. Фазовые равновесия и превращения. Физическая кинетика.
1
2
4
9. Электрическое поле. Проводники,
диэлектрики в электрическом поле.
2
2
8
10. Постоянный электрический ток.
Электрические цепи.
2
2
8
11. Магнитное поле в вакууме и веществе. Электромагнитная индукция.
Переменный ток. Электрические цепи
с изменяющимся током.
2
2
8
Итого
18
22
72
8
2.2. Содержание отдельных тем учебных дисциплин
Тема 1. Кинематика материальной точки. Виды движения. Кинематические характеристики.
Понятие материальной точки. Физические основы механики как науки о
простейших формах движения. Механическое движение. Скорость, ускорение.
Вращательное движение. Угловая скорость, угловое ускорение. Криволинейное
движение. Нормальное, тангенциальное ускорения.
Тема 2. Динамика материальной точки, твердого тела. Законы Ньютона. Динамические характеристики вращательного движения твердого тела.
Три закона Ньютона. Сила. Упругие силы и сила трения. Закон Всемирного
тяготения. Движение тел относительно инерциальных и неинерциальных систем
отсчета. Момент инерции. Момент силы.
Тема 3. Основные законы сохранения. Движение жидкостей и газов.
Закон сохранения импульса. Движение тел переменной массы. Работа, энергия и мощность. Закон сохранения энергии для замкнутых систем. Линии и трубки тока. Уравнение Бернулли. Вязкое течение. Ламинарный, турбулентный поток.
Формула Торричелли.
Тема 4. Основы механики упругих тел.
Упругие и пластические деформации. Закон Гука. Диаграмма деформации.
Потенциальная энергия деформации. Виды деформаций.
Тема 5. Молекулярно-кинетическая теория газов.
Основные понятия: давление, объем, температура, идеальный газ. Уравнение Клапейрона–Менделеева. Основное уравнение молекулярно-кинетической
теории газа. Барометрическая формула. Средняя квадратичная скорость частиц
газа. Универсальная газовая постоянная, постоянная Больцмана.
Тема 6. Основы термодинамики.
Внутренняя энергия. Первое начало термодинамики. Теплоемкость. Удельная, молярная теплоемкости. Равновесные процессы. Изопроцессы. Второе начало
термодинамики. Энтропия. Третье начало термодинамики (теорема Нернста).
Тепловые машины. Цикл Карно.
Тема 7. Агрегатные состояния вещества.
Твердое состояние вещества. Кристаллическая структура твердого тела.
Жидкости, их свойства. Поверхностное натяжение. Давление Лапласа. Смачиваемость. Капиллярные явления.
Тема 8. Фазовые равновесия и превращения. Физическая кинетика.
Испарение и компенсация. Критическое состояние. Изотермы Ван-дерВаальса. Плавление и кристаллизация. Диаграммы состояния.
9
Тема 9. Электрическое поле. Проводники и диэлектрики в электрическом поле.
Электрический заряд. Два рода заряда. Закон Кулона. Напряженность, потенциал электрического поля. Теорема Остроградского–Гаусса. Диполь, поле диполя. Проводники в электрическом поле. Электроемкость, конденсаторы. Энергия
электрического поля конденсатора. Последовательное, параллельное соединение
конденсаторов.
Тема 10. Постоянный электрический ток. Электрические цепи.
Сила тока. Электродвижущая сила, напряжение. Электрические цепи постоянного тока. Закон Ома для участка цепи, полной цепи, в дифференциальной
форме. Закон Джоуля–Ленца. Сложные электрические цепи. Правила Кирхгофа.
Электрический ток в различных средах.
Тема 11. Магнитное поле в вакууме и веществе. Электромагнитная индукция. Переменный ток. Электрические цепи с изменяющимся током.
Постоянное магнитное поле. Магнитное поле тока. Закон Био–Савара–
Лапласа. Магнитное поле тока различных проводников. Сила Ампера, определение направления силы Ампера. Работа по перемещению проводника с током в
магнитном поле. Сила Лоренца. Опыты Фарадея по электромагнитной индукции.
Вихревые токи. Явление самоиндукции. Получение переменного тока. Резонанс
напряжения и тока в цепях с изменяющимся током.
3. Информационное обеспечение учебной дисциплины
3.1. Вопросы к экзамену
Механика
1. Механическое движение. Модели пространства.
2. Кинематические характеристики механического движения: траектория,
перемещение, скорость, ускорение.
3. Виды движения. Поступательное движение, его характеристики.
4. Вращательное движение, его кинематические характеристики. Колебательное движение.
5. Тангенциальное, нормальное ускорения.
6. Взаимодействие, мера взаимодействия.
7. Инертность, мера инертности.
8. Законы динамики. Импульс силы, импульс.
9. Энергия, работа, мощность.
10. Вращательное движение твердого тела: момент силы, момент инерции.
10
11. Момент количества движения. Закон сохранения момента количества
движения.
12. Идеальная жидкость. Теорема неразрывности струи.
13. Уравнение Бернулли, формула Торричелли.
Молекулярная физика
1. Законы идеального газа.
2. Графическое представление изопроцессов.
3. Шкала температуры Кельвина.
4. Объединенный газовый закон.
5. Основное уравнение молекулярно-кинетической теории газа.
6. Универсальная газовая константа, постоянная Больцмана, их физический
смысл.
7. Реальный газ. Анализ уравнения Ван-дер-Ваальса.
8. Первое начало термодинамики.
9. Теплоемкость, удельная теплоемкость.
10. Работа при изотермическом процессе.
11. Адиабатный процесс.
Электричество и магнетизм
1. Два рода зарядов, их свойства.
2. Электрическое поле: силовой и энергетический характер поля.
3. Теорема Остроградского–Гаусса.
4. Диполь. Поле диполя.
5. Электроемкость, конденсаторы: последовательное, параллельное соединение конденсаторов.
6. Постоянный электрический ток. Закон Ома для участка цепи, полной цепи,
в дифференциальной форме.
7. Работа, мощность в цепи постоянного тока, закон Джоуля–Ленца.
8. Электрический ток в электролитах. Законы М. Фарадея для электролиза.
9. Разветвленные электрические цепи. Правила Кирхгофа.
10. Магнитное поле тока. Закон Био–Савар–Лапласа.
11. Электромагнитная индукция. Получение переменного тока.
12. Резистор, конденсатор, индуктивность в цепи переменного тока.
13. Резонанс напряжения, резонанс тока в цепях переменного тока
11
3.2. Варианты контрольных работ
Вариант 1
Механика
1. Первую четверть пути мотоцикл проехал со скоростью 10 м/с, вторую –
со скоростью 15 м/с, третью – со скоростью 20 м/с и последнюю – со скоростью
5 м/с. Определить среднюю скорость мотоциклиста на всем пути.
2. Какой путь пройдет тело за время 10 сек от начала движения, если уравнения его движения: x = 2t2 +3t+4, y=3t2+4t–2, z =0 [м]?
3. Определить угловое ускорение маховика, частота вращения которого за
время 20 полных оборотов возросла равномерно от 1 об/с до 5 об/с.
Молекулярная физика
.
4. Газ нагревается в открытом сосуде при нормальном атмосферном давлении до температуры от 27 °С до 327 °С. Какое приращение получит при этом число молекул в единице объема газа?
5. В закрытом сосуде вместимостью 20 дм3 содержится одноатомный газ, плотность которого равна 0,2 кг/м3. Количество теплоты, необходимое для нагревания газа
на 80 К при этих условиях, равно 997 Дж. Найти молярную массу этого газа.
Электричество и магнетизм
6. Определить работу по перемещению заряда 10–8 Кл в электрическом поле
между двумя точками, находящимися на расстояниях 10 и 20 см от заряда 10–7 Кл.
7. Можно ли вместо двух параллельно соединенных электроплиток мощностью 500 Вт каждая включить электрокамин, который потребляет ток в 12,5 А
при напряжении в 127 В, если предохранитель рассчитан на ток, потребляемый
электроплитками?
Вариант 2
Механика
1. Камень брошен со скоростью 12 м/с под углом 30° к горизонту. На каком
расстоянии от места бросания камень упадет на землю?
2. Автомобиль идет по закруглению шоссе, радиус кривизны которого равен
200 м. Коэффициент трения колес о покрытие дороги – 0,1. При какой скорости
автомобиля начнется его занос?
3. Маховое колесо, имеющее момент инерции равный 125 кг·м2, вращается,
делая 15 об/с. После того как на колесо перестал действовать вращающий момент
сил, оно остановилось, сделав 300 оборотов. Найти момент сил трения.
12
Молекулярная физика
1. Кислород был нагрет при неизменном объеме 50 л. При этом давление газа изменилось на 0,5 МПа. Найти теплоту, сообщенную газу.
2.Найти удельные теплоемкости су и ср некоторого двухатомного газа, если
плотность его при нормальных условиях составляет 1,43 кг/м3.
Электричество и магнетизм
1. Воздушный конденсатор, заряженный до разности потенциалов 800 В, соединяется параллельно с одинаковым по размерам незаряженным конденсатором,
заполненным диэлектриком. Какова диэлектрическая проницаемость диэлектрика, если после соединения разность потенциалов равна 100 В?
2. Определить сечение медных проводов, отводящих ток от генератора
мощностью 103 кВт, если ток передается на трансформатор под напряжением
15 кВ. Плотность тока в проводе не должна превышать 10 А/мм2.
Вариант 3
Механика
1. Шайба, пущенная по поверхности льда с начальной скоростью 20 м/с
остановилась через 40 с. Найти коэффициент трения шайбы об лед.
2. Материальная точка массой 0,1 г колеблется согласно уравнению
x = 5Sin 20t [см]. Определить максимальное значение возвращающей силы и кинетической энергии точки.
3. Автомобиль массой 5 т движется со скоростью 10 м/с по выпуклому мосту.
Определить силу давления автомобиля на мост в его верхней части, если радиус
кривизны моста равен 50 м.
Молекулярная физика
4. Сколько молекул кислорода содержится в объеме 10 м3, если при хаотическом движении со средней скоростью квадратичной 400 м/с они производят на
стенки сосуда давление в 104 Па?
5. Разность между удельными теплоемкостями при постоянном давлении и
постоянном объеме некоторого газа равна 260 Дж/кг·град. Определить молекулярный вес данного газа.
Электричество и магнетизм
6. Конденсаторы емкостью 1 мкФ и 2 мкФ заряжены до разности потенциалов: 20 В и 50 В, соответственно. После зарядки конденсаторы соединены
одноименными полюсами. Определить разность потенциалов между обкладками
конденсаторов после их соединения.
13
7. Две электрические лампочки включены в сеть параллельно. Сопротивление первой лампочки равно 360 Ом, сопротивление второй – 240 Ом. Какая из
лампочек поглощает большую мощность? Во сколько раз?
3.3. Список рекомендуемой литературы
1. Савельев, И. В. Курс общей физики /И. В. Савельев. – М.: ООО «Изд-во
Астрель», 2003. – Кн. 1. Механика.
2. . Савельев, И. В. Курс общей физики / И. В. Савельев. – М.: ООО Изд-во
Астрель», 2003. – Кн. 2. Электричество и магнетизм.
3. Савельев, И. В. Курс общей физики / И. В. Савельев. – М.: «Изд-во Астрель», 2003. – Кн.3. Молекулярная физика и термодинамика.
4. Сивухин, Д. В. Общий курс физики: в 3 т. / Д. В. Сивухин. – М.:Наука, 1998.
5. Трофимова, Т. И. Курс физики /Т. И. Трофимова. – М.: Высш. школа, 2000.
6. Детлаф, А. А. Курс физики / А. А.Детлаф, Б. М. Яворский. – М.: Высш.
школа, 2000.
7. Стрелков, С. П. Механика / С. П. Стрелков. – М.: Наука, 1975.
8. Кикоин, А. К. Молекулярная физика / А. К. Кикоин, И. К. Кикоин. – М.:
Наука, 1976.
9. Калашников, С. Г. Электричество / С. Г. Калашников. – М.: Наука, 1985.
10. Приданов, В. Г. Краткий курс лекций по общей физике: в 2 ч. /
В. Г. Приданов. – Новосибирск, 2005. – Ч.1. Механика. Молекулярная физика. Ч.
2. Электричество и магнетизм. Оптика.
11. Алексеев, В. В. Физика. Раздел «Механика» / В. В.Алексеев. – Новосибирск, 2006.
12. Учебная программа по курсу общей физики / Л. А. Борыняк, Г. Ф. Сивых:
изд. НГПУ. – Новосибирск, 2001.
14
II. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
УМК предназначен для самостоятельного изучения курса физики студентами заочного отделения.
В состав УМК включены следующие элементы:
• рабочая программа по курсу «Физика»;
• теоретический материал по дисциплине;
• варианты контрольных работ;
• перечень вопросов к экзамену;
• комбинированные тестовые задания;
• список рекомендуемой литературы.
Основой профессиональной подготовки студентов факультета технологии и
предпринимательства является цикл дисциплин, объединенных в курсе «Прикладная
механика», в который входят: «Технология конструкционных материалов», «Теоретическая механика», «Сопротивление материалов», «Теория механизмов и машин»,
«Детали машин», «Гидравлика и гидравлические машины», «Теплотехника и тепловые машины» и др. Бесспорно, все они базируются на физике. Физика в настоящее
время занимает лидирующее положение среди естественных наук, что обусловлено
многообразием идей и методов исследования объектов.
Содержание курса организовано с учетом опыта преподавания физики на факультете технологии и предпринимательства студентам заочной формы обучения.
Методологическую основу курса составляет диалектический материализм.
Методическими особенностями данного курса являются:
 использование математического аппарата с целью иллюстрации эмпирических возможностей для анализа физических проблем;
 большое количество примеров из практической деятельности человека, демонстрирующих область применения рассматриваемых физических законов;
 самостоятельное изучение студентами ряда вопросов программы.
 для проверки усвоения учебного материала предложен широкий объем комбинированных тестов.
В качестве контрольных мероприятий предусмотрены:
1) контрольные работы;
2) экзамен.
15
В результате освоения курса физики студент обязан знать основные физические понятия, определения, законы, модели, должен уметь представлять в виде
упрощенной физической модели многообразие практических задач и описывать
поведение объектов на основе физических законов.
В предлагаемом учебно-методическом комплексе студентам заочной формы
обучения предлагается развернутый курс лекций с минимальным объемом математического аппарата, разобранные примеры экспериментально-теоретических
задач, анализ решения задач.
Для успешного усвоения всех объектов дисциплины «Физика» при самостоятельной работе предлагается широкий арсенал комбинированных тестов, работа
с которыми, на наш взгляд, позволит решить основную задачу – подготовиться к
выполнению контрольных мероприятий: контрольной работы и экзамена.
16
III. ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
ПО ДИСЦИПЛИНЕ «ФИЗИКА»
1. Механика
1.1. Кинематика
1.1.1. Механическое движение
Простейшей формой движения материи является механическое движение, которое
состоит в перемещении тел или их частей друг относительно друга. А поскольку это так,
то если имеется одно единственное тело в пространстве, где других тел нет, то о движении этого одного тела ничего сказать нельзя, так как нет ничего, по отношению к чему
оно могло бы менять свое положение. Значит, для изучения механического движения
необходимо обязательно указывать, по отношению к каким другим телам происходит
это движение. Это первое. Второе: всякое движение происходит как в пространстве, так
и во времени, поэтому для описания движения необходимо также определять время. Это
делается с помощью часов.
Вот такая совокупность отсчитывающих время часов и неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, называется системой отсчета.
Характер любого движения оказывается различным в зависимости от того, относительно каких тел рассматривается данное движение. (Человек идет по вагону набирающего ход поезда: относительно вагона движение человека равномерное; относительно
Земли – ускоренное.) Это обстоятельство называется относительностью движения. Таким образом, всякое движение относительно. Отвечая на вопрос, покоится тело или движется и как движется, необходимо указать систему отсчета.
Для изучения движения необходимо прежде всего научиться его описывать. Раздел механики, в котором изучается движение без рассмотрения причин, его вызывающих, называется кинематикой.
Описание движения тела означает указание для каждого момента времени положения в пространстве и скорости тела. Положение в пространстве задается с помощью
какой-либо системы координат, связанной с телами, образующими систему отсчета,
например, декартовой системы координат. В этой системе координат (рис. 1.1.1) положение любой точки А определяется заданием трех чисел – декартовых координат X, Y,
Z.
17
Рис. 1.1.1
1.1.2. Скорость
Рассмотрим скорость материальной точки. Материальная точка – это тело, размерами которого в условиях конкретной задачи можно пренебречь. Например, при
решении задачи о движении Земли вокруг Солнца размерами Земли (R ~ 6400 км)
можно пренебречь по сравнению с расстоянием до Солнца (~150 · 106 км) и считать
Землю материальной точкой.
Так вот, материальная точка при своем движении описывает некоторую в
общем случае кривую линию, которая называется траекторией.
Пусть материальная точка переместилась вдоль траектории из 1 в 2 (рис. 1.1.2).
Рис. 1.1.2
Расстояние вдоль траектории между точками 1 и 2 называется путем, пройденным частицей (материальной точкой). Путь часто обозначается буквой S .
Прямолинейный отрезок, проведенный из 1 в 2 называется перемещением (обозначается r ). Перемещение – вектор, т. е. величина, характеризующаяся не только
численным значением, но и направлением. Отметим, что путь – это скаляр.
Если за равные промежутки времени материальная точка проходит равные
пути, то движение называется равномерным. Для количественной характеристики
равномерного движения вводится величина, равная отношению пройденного пути
к промежутку времени, за который этот путь пройден. Эту величину называют
скоростью. В физике под скоростью понимается векторная величина, характеризующая не только быстроту перемещения, но и направление движения в каждый
момент времени. Если разбить траекторию на бесконечно малые участки S , то
каждому участку можно поставить в соответствие бесконечно малое перемещение
r (рис. 1.1.3). Отношение r ( t – промежуток времени, за который материальt
ная точка прошла путь S или совершила перемещение r ) даст значение средней скорости за время t . Если брать значения t все меньше и меньше  t  0 ,
18
то в пределе это отношение r дает значение скорости v в начальный момент
t
r
времени: v  im .
t 0
t
Рис. 1.1.3
Предел отношения изменения функции к изменению аргумента, стремящегося к
нулю, есть производная от этой функции по аргументу. Значит, скорость есть производная от перемещения по времени:
dr
.
v
dt
Модуль скорости, т. е. ее величину, можно определить следующим образом:
r
r
.
 im
t 0 t
t 0 t
v  v  im
Чем меньше будут участки S , на которые мы будем разбивать траекторию, тем
меньшие перемещения r будут соответствовать этим участкам. Это соответствует
уменьшению промежутков времени t , и различие между S и r будет становиться
все меньше. В пределе
S
im
 1.
t 0
r
Значит, в выражении для модуля скорости числитель
S dS

t 0 t
dt
v  im
r
можно заменить на S :
.
Модуль скорости равен производной от пути по времени.
При равномерном движении отношение
S
 const (по определению). Значит,
t
модуль скорости постоянен, но направление скорости может меняться.
Пример 1. Одновременно из одного и того же пункта выезжают две автомашины, которые движутся в одном направлении прямолинейно. Зависимость пройденного
автомобилями
пути
от
времени
выражается
уравнениями:
2
2
3
s1  at  bt ; s2  ct  kt  et . Необходимо найти модуль относительной скорости автомобилей.
Решение. Модуль скорости первого автомобиля равен v1  ds1  a  2bt ; модуль
dt
скорости второго –
ds
v2  2  c  2kt  3et 2 .
dt
Модуль относительной скорости первого ав-
томобиля по отношению ко второму составит
19
v  v1  v2  a  2  m  k  t  3et 2 .
Пример 2. Тело движется так, что модули скорости его в течение каждого из n
равных промежутков времени равны, соответственно, v1 , v2 ,..., vn . Каков модуль
средней скорости тела?
Решение. Суммарный путь, пройденный телом, равен s  v1t  v2t  ...  vnt . Полное
время, затраченное на путь, равно t p  nt . Модуль средней скорости на всем пути соn
ставит v  s  1  vi .
tp
n
i 1
1.1.3. Ускорение
В общем же случае скорость может меняться как по величине, так и по
направлению. Предел отношения изменения вектора скорости к промежутку времени, за который это изменение произошло, при промежутке времени, стремящемся к нулю, называется ускорением, т. е. ускорение есть производная от вектора скорости по времени:
dv
.
a
dt
Если ускорение постоянно по величине, т. е. по модулю, то движение является
равноускоренным и величину ускорения можно вычислить, поделив разность двух
значений скорости на промежуток времени t :
v v
a 2 1.
t
Пример 3. Зависимость пройденного телом пути от времени задается уравнением s  A  Bt  Ct 2  Dt 3 , где C  0,1м / с 2 ; D  0,03 м / с3 . Определить: 1) через какое время
после начала движения ускорение а тела будет равно 2 м / с 2 ; 2) среднее ускорение а
тела за этот промежуток времени.
Решение. Модуль скорости выражается первой производной от пути по времеds
 B  2Ct  3Dt 2 . Ускорение выражается первой производной от скорости по
dt
времени: a  dv  2C  6Dt . По условию, через t секунд ускорение примет значение
dt
a  2C
a  2 м / с 2 . Отсюда t 
 10  c  . Из выражения для скорости имеем: v0  B – значе6D
ние скорости в начальный момент времени; t10  B  2  0,110  3  0,03 102  ( B  11)  c  –
ни:
v
значение скорости в момент времени 10 с после начала движения. Среднее ускорение
за промежуток времени 10 с будет равно:
a 
v10  v0 B  11  B

 1,1  м с 2  .
t
10
Пример 4. Определить зависимость пути от времени, если ускорение тела пропорционально квадрату скорости и направлено в сторону, противоположную ей.
Решение. По условию a 
dv
 kv 2 . Отсюда, разделяя переменные, получаем:
dt
dv
dv
1
 kdt   2  k  dt   kt  const . При
2
v
v
v
t  0 скорость равна v  v0 . Значит,
20
const 
v0
1
1
1 ktv  1
.
  kt   0
v
v0
v
v0
v0
ktv0  1
v0
dt . Интегрируя, получаем: s  1 n  kv0t  1  const .
1  ktv0
k
Для определения постоянной интегрирования имеем: при t  0 s  s0 , значит, const  s0 .
Поскольку
v
ds
,
dt
Окончательно имеем:
то ds 
s  s0 
1
n  kv t  1 .
k
1.1.4. Угловая скорость и угловое ускорение
Любое механическое движение твердого тела может быть разложено на два
основных вида движения: поступательное и вращательное. Поступательное движение – это такое движение, при котором любая прямая, связанная с движущимся
телом, остается параллельной самой себе. При вращательном движении все точки
тела движутся по окружностям, центры которых лежат на одной и той же прямой,
называемой осью вращения. Ось вращения может находиться и вне тела.
Когда о теле говорят как о материальной точке, т. е. отвлекаются от его размеров, то понятие вращательного движения вокруг проходящей через него оси к
такому телу неприемлемо.
Вращательное движение можно характеризовать угловой скоростью и угловым ускорением.
Угловой скоростью называется предел отношения изменения угла поворота
к промежутку времени, за который это изменение произошло, при промежутке
времени, стремящемся к нулю, т. е. угловая скорость есть производная от угла поворота по времени. В кинематике бесконечно малые углы поворота рассматривают как векторы, считая модуль вектора d равным углу поворота, а направление
определяют правилом правого винта. (Векторы, направление которых связывается
с направлением вращения, называются псевдовекторами. Эти векторы не имеют
точек приложения и могут откладываться от любой точки оси.) Исходя из данного
определения угловой скорости, можно записать

d
.
dt
Если угловая скорость постоянна, то вращательное движение равномерное, и
модуль угловой скорости будет равен


,
t
где  – конечный угол поворота за время t .
Равномерное вращение можно характеризовать периодом T (временем одного полного оборота). Один полный оборот соответствует углу поворота 2 .
Значит, времени вращения t  T соответствует угол поворота 2 . Отсюда


t

2
2
T 
.
T

21
Число оборотов в единицу времени называется частотой вращения. Значит,
частота равна

1 

.
T 2
Пусть за время t величина угловой скорости изменилась на  . Предел
отношения изменения угловой скорости к промежутку времени, за который это
изменение произошло, при промежутке времени, стремящемся к нулю, называется угловым ускорением, т. е., по определению, угловое ускорение есть векторная
величина, равная производной от угловой скорости по времени:
 
d
.
dt
При вращательном движении тела выделяют и линейную скорость. Это скорость, с которой точка движется по окружности. Величина линейной скорости, т. е.
ее модуль, любой точки вращающегося тела определяется угловой скоростью и
расстоянием рассматриваемой точки от оси вращения. Пусть за время  t тело повернулось на малый угол  (рис. 1.1.4).
Рис. 1.1.4
Точка тела, находящаяся от оси вращения на расстоянии R , проходит при
этом путь S  R , и модуль линейной скорости составляет
v  im
t 0
S


 im R
 R im
 R .

t

0

t

0
t
t
t
Рассматривая радиус R как радиус-вектор точки, последнее равенство можно записать в векторном виде v   R  . Но   R . Значит, действительно
v   RSin  R    R . Направление вектора v определяется правилом правого вин-
та, т. е. вектор v направлен по касательной к окружности в сторону вращения.
Пример 5. Найти радиус вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2,5 раза больше линейной скорости v2
точки, лежащей на 5 см ближе к оси колеса.
Решение. Угловая скорость всех точек вращающегося колеса одинакова и
связана с линейной скоростью любой точки колеса соотношением v   R , где R –
расстояние точки от оси вращения. Обозначим через R1 радиус обода колеса. Тогда расстояние до оси от точки, лежащей на 5 см ближе к оси, будет
R2  R1  0,05  м  . В силу равенства угловых скоростей обеих точек получаем:
v1
v2
.

R1 R1  0,05
По условию, v1  2,5v2 . Отсюда
22
2,5
1

 R1  0,0833  м  .
R1 R1  0,05
Пример 6. Колесо, вращаясь равноускоренно, достигло угловой скорости
  20 рад с через N  10 оборотов после начала вращения. Найти угловое ускорение колеса.
Решение. При равнопеременном вращательном движении имеют место следующие два уравнения движения:
t2
,
2
  0   t .
  0t 
По условию 0  0 , и уравнения принимают вид:  
t2
2
и    t . Решая совмест-
2
но эти уравнения и учитывая, что   2 N , получаем окончательно:   
4 N
 3, 2( рад с ) .
2
1.1.5. Нормальное и тангенциальное ускорения
Для того чтобы тело двигалось криволинейно, линейная скорость каждой
точки тела должна постоянно менять свое направление. При любом положении
точки это направление есть направление касательной к траектории. Значит, точка
должна постоянно испытывать ускорение, направленное к центру кривизны, т. е.
перпендикулярно направлению скорости. Это ускорение называется нормальным.
Если криволинейное движение неравномерное и линейная скорость меняется не только по направлению, но и по величине, значит, движущееся тело испытывает ускорение и в направлении вектора скорости, т. е. в направлении касательной к траектории. Это ускорение называется тангенциальным.
Получим выражения для нормального и тангенциального ускорений. Рассмотрим плоское движение, т. е. такое, при котором все участки траектории частицы лежат в одной плоскости (рис. 1.1.5). Вектор v задает скорость частицы
(точки) A в момент времени t . За время  t точка перешла в положение B и
приобрела скорость, отличную от v как по модулю, так и по направлению и равную v1  v  v . Перенесем вектор v1 в точку A и найдем изменение скорости v .
Разложим вектор v на две составляющие. Для этого из точки A по направлению
скорости v отложим вектор AD , равный по модулю v1 . Очевидно, что вектор CD ,
равный v , определяет изменение скорости по модулю за время  t : v  v1  v .
Вторая же составляющая вектора v вектор vn характеризует изменение скорости за время  t по направлению.
23
Рис. 1.1.5
Тангенциальная составляющая ускорения:
v
v dv
 im
 ,
t 0 t
t 0 t
dt
a  im
т. е. равна производной по времени от модуля скорости (характеризует
быстроту изменения скорости по модулю).
Допустим, что точка B достаточно близка к точке A , вследствие чего участок криволинейной траектории можно считать дугой окружности радиуса r ,
причем дуга S мало отличается от хорды AB . Тогда AOB ~ EAD , откуда следует
vn vv1
vn v1

 . Но AB  vt , значит
. При t  0 имеем v1  v . Поскольку это так,
t
r
AB r
то EAD стремится к нулю. EAD – равнобедренный, из чего следует, что ADE
между v и vn стремится к прямому. Следовательно, при t  0 векторы vn и v
оказываются взаимно перпендикулярными. Вектор v направлен по касательной к
траектории, значит, вектор vn направлен к центру кривизны траектории. Модуль
этой составляющей ускорения будет равен
vn v 2

t  0 t
r
an  im
.
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:
a
dv
 a  an .
dt
В зависимости от составляющих ускорения движение можно классифицировать следующим образом:
1) a  0, an  0 – прямолинейное равномерное движение;
2) a  const, an  0 – прямолинейное равнопеременное движение; при таком
движении
a  a 
v v2  v1

t t2  t1
. Если t1  0, v1  v0 , то a 
t
v  v0
, откуда v  v0  at . Проинt
t
at 2
тегрировав последнее выражение, получим S   vdt    v0  at  dt  v0t  ;
2
0
0
3) a  f  t  , an  0 – прямолинейное движение с переменным ускорением;
24
4)
a  0, an  const
– равномерное движение по окружности ( an  v
2
r
 r  const );
5) a  0, an  0 – равномерное криволинейное движение;
6) a  const, an  0 – криволинейное равнопеременное движение;
7) a  f  t  , an  0 – криволинейное движение с переменным ускорением.
Пример 7. Нормальное ускорение точки, движущейся по окружности радиусом r  4 м , изменяется по закону an  a  bt  ct 2 . Найти тангенциальное ускорение
точки; путь, пройденный точкой за время t1  6 c после начала движения; полное
ускорение в момент времени
t2 
2
c,
3
если
a  1 м с2 , b  3 м с3 , с  2,25 м с4 .
Решение. Нормальное ускорение связано с линейной скоростью соотношением an 
v2
R
, где R – радиус окружности. Значит, для линейной скорости имеем:
v  R(a  bt  ct 2 ) . Тангенциальное ускорение есть производная по времени от лиdv d
нейной скорости: a  
dt

R(a  bt  ct 2 )
dt
 . Тогда путь, пройденный точкой, выра-
t1
t1
0
0
зится интегралом от скорости: s   vdt   R(a  bt  ct 2 ) dt . После подстановки
v  4(1  3t  2, 25t )  2  3t ;
2
a 
для тангенциального ускорения получаем:
t1
d  2  3t 
3
 3 м с 2 ; путь равен s    2  3t  dt  2t  t 2  66 м .
2
dt
0
В момент времени
t2 
2
c
3
получаем: v  4 м с; an  4 м с2 ; a  a2  an2  5 м с2 .
Пример 8. Мяч брошен под углом   60 к горизонту со скоростью
v0  20 м с . Определить наибольшую высоту подъема и дальность полета. Сопротивлением воздуха пренебречь.
Решение. Вектор начальной скорости мяча можно разложить на две составляющие: горизонтальную vг  v0Cos и вертикальную vв  v0 Sin . Вверх мяч поднимается с начальной скоростью vв и ускорением g , направленным вниз. Для равнозамедленного движения скорость в произвольный момент времени равна
v  vв  gt . Через какое-то время t вертикальная скорость мяча обратится в нуль
0  vв  gt . Время подъема равно t 
ленном движении h  vвt 
vв v0 Sin

. Высота подъема при равнозамедg
g
v Sin gv02 Sin2 v02 Sin2
gt 2
 v0tSin 0


. Время опускания
2
g
2g 2
2g
мяча от верхней точки до уровня бросания равно времени подъема. Значит полное
время полета мяча равно 2t . Все это время мяч летит в горизонтальном направлении со скоростью vг , так как сопротивление воздуха не учитывается. Расстояние,
которое
пролетит
мяч
в
горизонтальном
направлении,
составит
25
2v0 Sin v02 Sin2

.
Подставляя
g
g
202 Sin2 60
202 Sin 120
h
 15 м; s 
 35 м .
2  9,8
9,8
s  v г 2t  v0Cos
данные
задачи,
получаем:
1.2. Законы Ньютона
1.2.1. Сила. Упругие силы и силы трения
Кинематика описывает движение тел, не затрагивая вызывающих его причин. Раздел механики, в котором изучается движение тел в связи с причинами,
обусловливающими тот или иной характер движения, называется динамикой.
Характер движения определяют действующие на тело силы. Силами называются действия тел друг на друга, создающие ускорения. Сила – векторная величина, имеющая направление создаваемого ею ускорения.
Любая сила обусловлена взаимодействием тел. Взаимодействия могут осуществляться как на расстоянии, так и при непосредственном соприкосновении тел.
Для того чтобы одно тело могло действовать на другое при непосредственном соприкосновении, первое тело должно быть в особом состоянии: чтобы рука
действовала на мяч, мышцы руки должны быть сокращены; пружина игрушечного пистолета должна быть перед выстрелом сжата и т. п. Сжатия, растяжения, изгибы, кручения – это изменения формы или объема тел по сравнению с исходным
состоянием. Такие изменения называются деформациями. Значит, чтобы действовать на другие тела при непосредственном соприкосновении данное тело должно
быть деформировано. Силы воздействия исчезают вместе с исчезновением деформации и называются упругими. Для растянутой или сжатой пружины
Fупр   kx .
Здесь F упр – упругая сила, x – удлинение пружины, k – коэффициент
жесткости пружины. Знак «минус» означает, что сила F упр и удлинение x противоположны по направлению.
При перемещении соприкасающихся поверхностей тел друг относительно
друга возникают силы трения. Эти силы возникают и при попытке вызвать
скольжение одной поверхности по другой. В первом случае – это сила трения
скольжения, во втором – сила трения покоя. Эти виды сил трения обусловлены
шероховатостью соприкасающихся поверхностей и силами межмолекулярного
притяжения. Максимальная сила трения покоя и сила трения скольжения не зависят от площади соприкосновения трущихся поверхностей и оказываются приблизительно пропорциональны величине силы нормального давления Fn , прижимающей трущиеся поверхности друг к другу:
Fтр  kFn .
26
Значение коэффициента трения k можно определить следующим образом.
Пусть тело находится на наклонной плоскости с углом наклона  (рис. 1.2.1).
Рис. 1.2.1
Оно придет в движение только тогда, когда тангенциальная составляющая
F силы тяжести P больше силы трения Fтр . Следовательно, в предельном случае
F  Fтр . Но F  PSin0 ; Fтр  kFn  kPCos0 , где  0 – угол, при котором начинается
скольжение тела по наклонной плоскости. Значит,
PSin 0  kPCos 0  k  tg 0 .
Величина коэффициента трения зависит от природы и состояния трущихся
поверхностей, в частности, от их шероховатости. В случае скольжения коэффициент трения является функцией скорости.
Силы трения в природе и технике могут играть как положительную, так и
отрицательную роль. При необходимости уменьшения сил трения скольжение поверхностей друг относительно друга заменяют качением одного тела по другому.
Трение качения подчиняется тем же законам, что и трение скольжения, но коэффициент трения в этом случае оказывается значительно меньшим.
Пример 1. Автомобиль весит 98000 Н. Во время движения на автомобиль
действует сила трения, равная 0,1 его веса. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью: 1) в гору с
уклоном 1 м на каждые 25 м пути; 2) под гору с тем же уклоном.
Решение. Сила, развиваемая мотором автомобиля, поднимающегося в гору,
идет на преодоление силы трения и на преодоление составляющей силы тяжести,
параллельной пути: А  F тр  F1 . При этом Fтр  kFn  kPCos и F1  PSin . Таким образом, сила тяги F  P  kCos  Sin  . Подставляя числовые значения задачи и учитывая, что Sin  1 25  0, 04; Cos  1 , получим: F  1370 H .
В случае с автомобилем, движущимся под гору, F  P  kCos  Sin   590H .
Если сила трения меньше составляющей силы тяжести, параллельной пути, т. е.
если PkCos  PSin , то F  0 . В этом случае, чтобы осуществить равномерное
движение автомобиля под гору, необходимо приложить задерживающую силу.
При отсутствии этой силы автомобиль будет двигаться под гору с ускорением
a  g  Sin  kCos  .
27
1.2.2. Первый закон Ньютона
Всякие силовые взаимодействия тел, рассматриваемые в классической механике (и взаимодействия при непосредственном соприкосновении тел, и взаимодействия тел на расстоянии), подчиняются законам Ньютона, которые являются
обобщением огромного человеческого опыта. Аналитическим путем они не могут
быть выведены.
Опыт показывает, что тела получают ускорения, т. е. изменяют свою скорость по величине или направлению только при действии на них других тел. Каждый раз, когда тело получает ускорение, можно указать другое тело, которое это
ускорение вызвало. Например, бросаемый мяч получает ускорение под действием
мышц руки; пуля, вылетающая из пистолета с большой скоростью под действием
пороховых газов, постепенно уменьшает свою скорость под действием встречного
воздуха и т. п. В случае если на данное тело никакие другие тела действовать не
будут, оно будет либо оставаться в покое, либо двигаться равномерно и прямолинейно, т. е. без ускорения. Проверить это практически невозможно, так как невозможно полностью устранить действие всех окружающих тел. Но чем тщательнее
устранены эти действия, тем ближе движение данного тела к прямолинейному и
равномерному. Например, шарик на горизонтальной поверхности, посыпанной
песком, быстро останавливается, а на гладкой стеклянной поверхности сохраняет
свою скорость практически неизменной.
Первый закон Ньютона (впервые установленный Галилеем) гласит: «Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока
воздействие со стороны других тел не заставит его изменить это состояние».
Покой, равномерное и прямолинейное движение означают, что ускорение
тела равно нулю. Значит, первый закон Ньютона можно переформулировать так:
«Скорость тела остается постоянной, пока воздействие со стороны других тел
не вызовет ее изменения».
Этот закон выполняется не во всех системах отсчета. Если одна система отсчета покоится, а другая движется относительно нее с некоторым ускорением, то
первый закон Ньютона в обеих системах одновременно выполняться не может,
так как в движущейся системе тело, покоящееся в первой системе, будет двигаться и двигаться ускоренно. А это противоречит первому закону Ньютона, так как
на тело никакие силы не действуют, и ускорение должно быть равно нулю.
Система отсчета, в которой выполняется первый закон Ньютона, называется
инерциальной, а сам закон – законом инерции.
Если первый закон Ньютона в системе отсчета не выполняется, то такая система называется неинерциальной.
Пусть какая-либо система отсчета движется относительно инерциальной системы отсчета равномерно и прямолинейно; в этом случае скорость тела в движущейся системе отсчета будет отличаться от скорости тела в инерциальной системе отсчета на постоянную добавку (относительную скорость движения систем). Значит, все изменения скорости тела будут одинаковыми в обеих системах
отсчета, а значит, одинаковы будут и ускорения тела относительно обеих систем.
28
Таким образом, если две системы отсчета движутся равномерно и прямолинейно друг относительно друга, то ускорения тел относительно обеих систем будут равны. (Скорости движения тел относительно обеих систем, конечно, будут
различны.) Отсюда следует, что если одна система отсчета инерциальна, то и другая тоже инерциальна, т. к. тело, на которое не действуют другие тела, будет двигаться относительно обеих систем с нулевым ускорением. Инерциальных систем
отсчета бесконечно много, так как любая система, движущаяся относительно
инерциальной прямолинейно и равномерно будет инерциальной.
Инерциальна с высокой степенью точности гелиоцентрическая система отсчета (центр – на Солнце, оси направлены на специальным образом выбранные
звезды). Система отсчета, связанная с Землей, неинерциальна. Земля совершает
криволинейное движение и суточное вращение по траектории вокруг Солнца
(значит, ее ускорение всегда отлично от нуля). Но ускорение Земли настолько мало, что часто можно считать систему отсчета, связанную с Землей, инерциальной.
Но не всегда! Иногда неинерциальность системы отсчета, связанной с Землей,
оказывает существенное влияние на характер рассматриваемых относительно нее
механических явлений. Например, расчет траекторий космических аппаратов без
учета неинерциальности системы отсчета, связанной с Землей, приведет к грубейшим ошибкам.
Относительно всех инерциальных систем отсчета тела получают одинаковые ускорения при одинаковых действиях на них со стороны других тел. «Все
инерциальные системы совершенно равноправны относительно причин ускорений» – принцип относительности Галилея.
Когда речь идет о скорости какого-либо тела, необходимо указать, относительно какой инерциальной системы она измерена, так как в разных инерциальных системах эта скорость будет различна, даже если на тело и не действовали
никакие другие силы. Ускорение же тела будет одинаковым относительно всех
инерциальных систем отсчета. Относительно движущегося вагона скорость тела
может быть равна нулю, тогда как относительно Земли оно может иметь скорость
до 100 км/час, а в гелиоцентрической системе отсчета скорость этого тела составит 30 км/с (скорость Земли в ее движении вокруг Солнца). Но если в вагоне
брошен мяч, то ускорение мяча будет одним и тем же и относительно вагона, и
относительно Земли, и относительно Солнца. По отношению к инерциальным системам отсчета ускорение абсолютно, а скорость относительна.
1.2.3. Второй закон Ньютона
Прежде чем перейти ко второму закону Ньютона, разберем, что такое масса.
Известно, что ускорение данного тела пропорционально действующей на тело силе:
F1 F2 F3


 ..........
a1 a2 a3
Однако при действии одинаковыми силами на различные тела эти тела приобретут разные ускорения. Разные тела в разной мере обладают свойствами
29
инертности. Что это такое? Всякое тело противится попыткам изменить его состояние движения. Это свойство тел называется инертностью.
Можно ввести понятие о мере инертности тел, считая меру инертности двух
тел одинаковой, если под действием одинаковых сил они получают одинаковое
ускорение, и считая меру инертности тем большей, чем меньше ускорение получает тело под действием данной силы. Таким образом, мера инертности тела
должна быть определена непосредственно механическим опытом – измерением
ускорения, создаваемого данной силой. Меру инертности тела называют массой.
Обычно ее обозначают буквами M или m .
Итак, масса тела есть его характерное свойство, определяющее соотношение между действующей на тело силой и сообщаемым ею телу ускорением. Так
как сила и ускорение пропорциональны друг другу, масса тела определяется как
отношение действующей на тело силы к ускорению:
m
F
.
a
Вычисленное по этой формуле значение массы для данного тела всегда будет иметь одно и то же значение, с какой бы силой мы не действовали на тело.
Вспомним теперь, что сила – вектор, имеющий направление создаваемого
ей ускорения. Значит, последнее равенство можно записать так:
F  ma .
Эта формула выражает основной закон движения, известный под названием
второго закона Ньютона. Формулируется закон так: «Сила, действующая на тело,
равна произведению массы тела на создаваемое этой силой ускорение, причем
направления силы и ускорения совпадают».
Вспомним, что ускорение есть предел отношения изменения скорости к
промежутку времени, за который это изменение произошло, при промежутке времени, стремящемся к нулю:
a  im
v
.
t
 mv
Значит, ma  m im v  im   , так как m  const при v  с ( с – скорость свеt
t
та в вакууме).
Произведение массы тела на его скорость называется импульсом тела:
P  mv .
Значит, ma  im
P dP
. Отсюда современная формулировка второго закона

t
dt
Ньютона: «Скорость изменения импульса тела равна действующей на тело силе»:
F
dP
.
dt
Во втором законе Ньютона заключен как частный случай первый закон (закон инерции). Действительно, из выражения F  ma следует, что при F  0 ускорение тоже равно нулю a  0 , т. е., если на тело не действуют силы (или равно30
действующая всех сил равна нулю), то и ускорение равно нулю, а значит, тело сохраняет состояние покоя или равномерного и прямолинейного движения.
Примеров проявления второго закона Ньютона очень много. Электровоз
разгоняет поезд с тем меньшим ускорением, чем больше полная масса поезда. Отталкивая с одинаковой силой от берега пустую и тяжело груженую лодку, заставим первую двигаться с большим ускорением, чем вторую и т. п. Как бы ни мала
была результирующая сила, действующая на тело, ускорение возникнет, но оно
может быть настолько малым, что потребуется много времени, чтобы вызвать заметное изменение скорости. На реке иногда приходится видеть, как человек, упираясь багром в борт большой баржи, тратит несколько минут на сообщение ей еле
заметной скорости.
Второй закон Ньютона справедлив при скоростях движения, много меньших
скорости света. Для элементарных частиц (электронов, протонов), разгоняемых в
ускорителях до субсветовых скоростей, закон не верен. Частицы разгоняются магнитным полем, действующим на них с постоянной силой. Согласно второму закону Ньютона, ускорение должно быть постоянным. Но при приближении значения скорости
частиц к скорости света (скорость частиц не может быть больше скорости света) она
растет все медленнее и медленнее, т. е. ускорение уменьшается.
Пример 2. Автомобиль движется со скоростью 45 км ч . Найти тормозной
путь, если с помощью тормозов может быть создана замедляющая сила, равная
2 3 веса автомобиля. Время реакции водителя равно 0, 7 с .
Решение. Поскольку реакция водителя t1  0, 7 c , автомобиль до начала торможения проходит путь s1  v0t1 . Массу автомобиля обозначим через m , тогда вес
его будет равен mg . Движение автомобиля при торможении считаем равнозамедленным с ускорением a , направленным против движения. Сила, создающая это
2
3
ускорение, равна F  mg и направлена против движения. В соответствии со вторым законом Ньютона модуль ускорения автомобиля будет равен a 
равнозамедленном
движении
модуль
конечной
скорости
F 2
 g . При
m 3
равен
нулю
v
vk  0  v0  at2  t2  0 . Путь, пройденный автомобилем при равнозамедленном
a
движении равен
s2  v0t2 
at22 3v02 3v02 3v02
.



2
2g 4g 4g
Полный путь до остановки автомобиля равен
s  s1  s2  v0t1 
3v02
 20,7 м .
4g
Пример 3. На наклонной плоскости с углом к горизонту   30 движется
тело 2 массой m1  1 кг , связанное невесомой нитью с телом 1 такой же массы
(рис. 1.2.2). Найти ускорение этих тел и силу натяжения нити. Трением в блоке
пренебречь. Коэффициент трения тела 2 о наклонную плоскость равен k  0,1 .
31
Рис. 1.2.2
Решение. На тело 2 действуют: составляющая силы веса, параллельная
плоскости F1  m2 gSin ; сила трения Fтр  kN  km2 g ; сила натяжения нити Fн ,
направленная противоположно первым двум. На тело 1 действуют сила веса m1 g и
сила натяжения нити Fн . Вся система движется с ускорением а . В соответствии
со вторым законом Ньютона имеем два уравнения:
m1a  m1 g  Fн , m2 a  Fн  m2 gSin  km2 gCos .
Знаки в уравнениях определяются направлением движения тел: тело 1 опускается вниз, тело 2 поднимается вверх по наклонной плоскости. Обратное движение могло бы иметь место, если бы было F1  m2 gSin  m1 g  Fтр . При равенстве
масс тел это невозможно. Из первого уравнения имеем: Fн  m1  g  a  . Подставив
это выражение во второе уравнение, получим: a  g
m1  m2  Sin  kCos 
 м
 2, 02  2  .
m1  m2
с 
Отсюда для силы натяжения нити имеем:
Fн 
m1m2 1  Sin  kCos  g
 7, 77 ( H ) .
m1  m2
Пример 4. На какое расстояние отклонится пуля массой 6 г под действием
бокового ветра, создающего силу 0, 012 Н , если начальная скорость пули 600 м с ,
а дистанция стрельбы 300 м ? Угол между направлениями ветра и стрельбы 90 .
Движение пули – равнозамедленное ( а  450 м с2 ).
Решение. Время полета пули определится из выражения для расстояния,
пройденного пулей при равнозамедленном движении: s  v0t 
at  2v0t  2s  0  t1,2 
2

a

600  360000  2  450  300
,
450
t1  0, 667 c; t2  2 c .
ускорении
v0  v02  2as
at 2
. Отсюда
2
Второй корень нереален, т. к. при заданном отрицательном
пуля
остановится
за
меньшее
время:
32
vk  0  v0  at  t  v0  a   600 450  1,333 (c) . Ускорение пули, сообщаемое ветром,
a1  F m . Тогда отклонение пули составит s1 
a1t12 Ft12

 0, 45  м  .
2
2m
1.2.4. Третий закон Ньютона
Теперь рассмотрим третий закон Ньютона. Множество примеров показывает, что силы носят взаимный характер, так что силовые действия тел друг на друга
всегда представляют собой взаимодействия. Если тело 1 действует на тело 2 с силой F21 , то тело 2 действует на тело 1 с силой F12 . Например, при столкновении
двух шаров оба получают ускорения; при формировании железнодорожного состава вагоны наталкиваются друг на друга, при этом буферные пружины сжимаются у обоих вагонов; Земля притягивает Луну, заставляя ее двигаться по криволинейной траектории, но и Луна притягивает Землю, что проявляется в виде океанских приливов и т. п.
Опытные динамометрические измерения показывают, что силы, с которыми
действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению:
F21   F12 .
Это закон равенства действия и противодействия, открытый Ньютоном и
названный им третьим законом движения.
Силы всегда возникают попарно: всякой силе, действующей на какоенибудь тело, можно поставить в соответствие силу, действующую со стороны
этого тела на тело, взаимодействующее с данным.
Закон равенства действия и противодействия выполняется не всегда. (Он
всегда справедлив только для контактных взаимодействий и взаимодействий покоящихся тел.) Примером нарушения действия закона может служить взаимодействие двух электрических зарядов, расходящихся перпендикулярно друг другу.
1.2.5. Закон всемирного тяготения
Исходя из основных законов динамики и законов Кеплера (законов движения планет), Ньютон открыл всеобщий закон всемирного тяготения: между двумя
любыми материальными точками действует сила взаимного притяжения, прямо
пропорциональная произведению масс этих точек m1 и m2 и обратно пропорциональная квадрату расстояния между ними r 2 :
F G
m1m2
r2
.
Эта сила называется гравитационной (или силой всемирного тяготения).
Силы тяготения являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. G = 6,6720·10–11 Н·м2/кг2 – гравитационная
постоянная.
33
Гравитационное взаимодействие между телами осуществляется с помощью
поля тяготения или гравитационного поля. Это поле порождается самими телами.
Основное свойство поля тяготения заключается в том, что на всякое тело массой
m , внесенное в это поле, действует сила тяготения.
На любое тело, расположенное вблизи Земли, действует сила тяготения, под
влиянием которой, согласно второму закону Ньютона, тело начнет двигаться к
Земле с постоянным ускорением. Это означает, что в системе отсчета, связанной с
Землей, на всякое тело массой m действует сила P  mg , называемая силой тяжести. (Сейчас мы пренебрегаем неинерциальностью системы отсчета, связанной с
Землей.) Когда тело покоится относительно поверхности Земли, сила P уравновешивается реакцией Fr подвеса или опоры, удерживающих тело от падения
Fr   P . Согласно третьему закону Ньютона, тело в этом случае действует на подвес или опору с силой Q , равной  Fr , т. е. с силой Q  P  mg . Сила Q , с которой
тело действует на подвес или опору, называется весом тела. Эта сила равна mg
лишь в том случае, если тело и опора (или подвес) неподвижны относительно
Земли. В случае их движения с некоторым ускорением a вес Q не будет равен mg . Это можно пояснить следующим примером.
Пусть подвес (рис. 1.2.3) в виде закрепленной с одного конца пружины
движется вместе с телом с ускорением a . Тогда уравнение движения тела (второй
закон Ньютона) будет иметь вид P  Fr  ma , где Fr – реакция подвеса, т. е. сила, с
которой пружина действует на тело. Тело действует на пружину в соответствии с
третьим законом Ньютона с силой, равной  Fr , которая по определению представляет собой вес тела Q в этих условиях. Заменив реакцию Fr силой Q , а силу
тяжести – произведением mg , получим
P  Q  ma  Q  m  g  a  .
Это равенство выражает вес тела в общем случае. Оно справедливо для подвеса или опоры любого вида.
Предположим, что тело и подвес движутся в вертикальном направлении
(вверх, вниз) и ускорение a отрицательно, когда оно направлено вверх (противоположно ускорению g ) и положительно, когда оно направлено вниз (одинаково с
ускорением g ). Из последнего равенства видно, что вес Q может быть как больше, так и меньше силы тяжести P  mg . Когда a  0 , вес тела Q больше силы тяжести P . Когда a  0 , вес меньше силы тяжести. При свободном падении подвеса
a  g и сила Q , с которой тело действует на подвес, равна нулю. Наступает состояние невесомости. Космический корабль, летящий вокруг Земли с выключенными
двигателями, движется по круговой (или эллиптической) орбите с нормальным
ускорением g , вследствие чего тела внутри корабля находятся в состоянии невесомости – они не оказывают давления на соприкасающиеся с ними тела и стены
корабля.
34
Рис. 1.2.3
Часто путают силу тяжести P и вес тела Q . Это происходит из-за того, что
в случае неподвижной опоры силы P и Q совпадают по величине и направлению.
Однако эти силы приложены к разным телам: сила P приложена к самому телу,
сила Q приложена к подвесу. Кроме этого, сила P всегда равна mg независимо от
того, движется тело или покоится; сила веса Q зависит от ускорения, с которым
движутся опора и тело, причем Q может быть как больше, так и меньше mg (в состоянии невесомости Q  0 ).
Пример 5. Найти изменение ускорения свободного падения тела на глубине
h от поверхности земли. На какой глубине ускорение свободного падения составит 0,3 от ускорения свободного падения на поверхности Земли? Плотность Земли считать постоянной. Считать, что со стороны вышележащего слоя тело не испытывает никакого притяжения.
Решение. Обозначим массу тела через m , расстояние от центра Земли – через R1 , ускорение свободного падения на глубине h – через g1 . Тогда на глубине
h вес тела равен Q1  mg1 . С другой стороны, Q1  F1  G
mM 1
, где M 1 – масса земли в
R12
4
объеме шара радиусом R1 ; M 1   R13  , где  – средняя плотность Земли;
3
4
mg1  Gm  R1  . На поверхности Земли вес тела равен
3
g
R Rh
mM
4
Rh
Q  mg  G 2  Gm  R   1  1 
 g1  g
.
R
3
g
R
R
R
Если
g1
 0,3 , то h  0, 7 R .
g
35
1.2.6. Движение тел относительно инерциальных
и неинерциальных систем отсчета
Вернемся к вопросу об инерциальных и неинерциальных системах отсчета и
выясним, как различаются уравнения движения (второй закон Ньютона) в разных
системах отсчета.
Из принципа относительности Галилея следует, что в инерциальных системах силы, действующие на тело, совпадают: F  F  (это одна и та же сила в разных
системах отсчета). В инерциальных системах одинаковыми полагаются также
расстояния между телами, относительные скорости тел и массы тел.
А раз это так (силы, массы и ускорения одинаковы во всех инерциальных
системах), то из этого следует, что уравнения движения, в которые входят только
силы, массы и ускорения, не изменяются при переходе от одной инерциальной
системы отсчета к другой. В этом случае говорят, что уравнения динамики инвариантны относительно преобразований координат, соответствующих переходу от
одной инерциальной системы отсчета к другой.
Относительно всех инерциальных систем отсчета тело движется с одинаковым ускорением (подчеркнем, не скоростью, а ускорением). Любая неинерциальная система отсчета движется относительно инерциальных систем с некоторым
ускорением, поэтому ускорение тела в неинерциальной системе отсчета a будет
отличаться от ускорения a на некоторую величину w : a  a  w .
Пусть равнодействующая всех сил, действующих на тело со стороны других
тел, равна F . Тогда относительно любой инерциальной системы отсчета a 
Это
по
a  a  w 
второму закону Ньютона. В неинерциальной
F
.
m
системе отсчета
F
 w , следовательно, даже при F  0 (при отсутствии сил, действующих
m
на тело) тело будет двигаться по отношению к неинерциальной системе отсчета с
ускорением  w , т. е. так, как будто бы на него действует сила mw . Эта сила
называется силой инерции.
Значит, в неинерциальной системе отсчета можно пользоваться уравнениями Ньютона для описания движения тела, если наряду с силами, обусловленными
воздействиями тел друг на друга, учитывать силы инерции Fи , равные произведению массы тела на взятую с обратным знаком разность ускорений тела по отношению к инерциальной и неинерциальной системам отсчета: Fи  m  a  a  mw.
Тогда уравнение второго закона Ньютона в неинерциальной системе отсчета будет иметь вид:
ma  F  Fи .
В силу неинерциальности системы отсчета, связанной с Землей, сила тяжести
несколько отличается от силы притяжения тела Землей. Ускорение g , наблюдаемое
относительно Земли, обусловлено действием силы Fg , с которой тело притягивается
Землей, и силы Fц (центробежной силы инерции). Результирующая этих сил
(рис. 1.2.4): P  Fg  Fц  mg есть сила тяжести. Отличие P от Fg невелико ( Fg пример36
но в 300 раз больше Fu ). Тем не менее это различие приводит к тому, что ускорение g
зависит от широты местности: на экваторе оно минимально ( g  9, 78 м/с2), на полюсах
– максимально ( g  9,83 м/с2).
Рис. 1.2.4
В инерциальной системе отсчета (например, в гелиоцентрической системе)
свободно падающее на Земле тело движется с ускорением a 
Fg
m
, а не g .
Пример 6. Необходимо получить выражение для силы инерции при поступательном движении.
Решение. Пусть на тележке к штативу подвешен шарик массой m . Пока тележка покоится или движется равномерно и прямолинейно, нить, удерживающая
шарик, занимает вертикальное положение, и сила тяжести Р уравновешивается
реакцией нити Т .
Если тележку привести в поступательное движение с ускорением а0
(рис. 1.2.5), то нить начнет отклоняться назад до такого угла  , пока результирующая сила F  P  T не обеспечит ускорение шарика а0 .
Рис. 1.2.5
Таким образом, результирующая сила F направлена в сторону ускорения
тележки а0 и для установившегося движения шарика (шарик теперь движется
вместе с тележкой с ускорением а0 ) равна F  mgtg  ma0 . Отсюда угол отклонения нити от вертикали tg  a0 g . Относительно системы отсчета, связанной с
ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F
уравновешивается равной и противоположно направленной силой Fи , которая яв37
ляется ничем иным, как силой инерции, так как никакие другие силы на шарик не
действуют. Таким образом, Fи   ma0 .
Пример 7. Необходимо получить выражение для силы инерции при вращательном движении.
Решение. Пусть диск равномерно вращается с угловой скоростью   const
вокруг вертикальной оси, проходящей через его центр. На диске у края установлен штатив, на котором укреплен на нити шарик (рис. 1.2.6). При вращении диска
шарик отклоняется от вертикали.
Рис. 1.2.6
В инерциальной системе отсчета, связанной, например, с помещением, где
установлен диск, шарик равномерно вращается по окружности радиусом R (расстояние по горизонтали от точки крепления шарика до оси вращения). Следовательно, на него действует сила F  man , где an – нормальное ускорение шарика.
Так как an   2 R , то F  m 2 R . Направлена эта сила перпендикулярно оси вращения и уравновешивается равнодействующей силы тяжести Р и силы натяжения
нити Т : F  P  T . При установившемся движении шарика F  mgtg  m 2 R . Отсюда tg   2 R g .
Относительно системы отсчета, связанной с диском, шарик покоится, что
возможно только в случае, если сила F уравновешивается равной ей и противоположно направленной силой Fц , которая является ничем иным как силой инерции, так как на тело никакие другие силы не действуют. Сила Fц называется центробежной силой инерции, направлена по горизонтали от оси вращения диска и
равна Fц  m 2 R .
Пример 8. Считая Землю шарообразной, найти зависимость ускорения свободного падения от широты местности. Вычислить g на полюсе, экваторе и широте Одессы (   46,5 ).
38
Рис. 1.2.7
Решение. Вес тела P  mg является равнодействующей силы тяготения
F G
mM
R2
(М – масса Земли) и центробежной силы инерции Fц  m 2 RCos , где 
– широта местности,  – угловая скорость вращения Земли (рис. 1.2.7). По теореме косинусов P2  Fg2  Fц2  2Fg FцCos , откуда
g  G2
M2
R4
  4 R 2Cos 2  2G
M 2
 Cos ; g п  9,83 м с 2 ; g э  9, 78 м с 2 ; g o  9,81 м с 2 .
R
1.3. Основные законы сохранения
1.3.1. Закон сохранения импульса
Введем понятие замкнутой механической системы. Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не
принадлежащими данной системе. В соответствии с этим силы, действующие на
тела системы, можно подразделить на внутренние и внешние. Внутренними называются силы, с которыми на данное тело действуют остальные тела системы;
внешними – силы, обусловленные воздействием тел, не принадлежащих системе.
В случае если внешние силы отсутствуют, система называется замкнутой.
Для замкнутых систем оказываются неизменными (сохраняются) в процессе
движения три физических величины: энергия, импульс и момент импульса. В соответствии с этим имеют место три закона сохранения: закон сохранения энергии,
закон сохранения импульса и закон сохранения момента импульса.
Законы сохранения являются мощным инструментом решения научноисследовательских задач. Часто бывает, что точное решение уравнений движения
оказывается крайне сложным. В этих случаях с помощью законов сохранения
можно и без решения уравнений движения получить важные данные о протекании
механических явлений. Законы сохранения не зависят от характера действующих
сил. Поэтому с их помощью можно получить важные сведения о поведении механических систем даже в тех случаях, когда силы оказываются неизвестными.
Законы сохранения обладают гораздо большей общностью, чем законы
Ньютона (хотя они выводятся из законов Ньютона). Законы сохранения остаются
строго справедливыми даже тогда, когда законы Ньютона претерпевают нарушения. Все три закона сохранения являются точными законами, строго выполняющимися во всех областях.
Наиболее прост для понимания и легко доказывается закон сохранения импульса.
Рассмотрим механическую систему, состоящую из n тел, масса и скорость
которых, соответственно, равны m1 , m2 ,..., mn и v1 , v2 ,..., vn . Пусть F1, F2,..., Fn – равнодействующие внутренних сил, действующих на каждое из этих тел, а F1 , F2 ,..., Fn –
равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из
n тел механической системы:
39
d
 m1v1   F1  F1
dt
d
 m2v2   F2  F2
dt
...............................
d
 mn vn   Fn  Fn.
dt
Складывая почленно эти уравнения, получим:
d
 m1v1  m2v2  ...  mnvn   F1 F2  ...  Fn  F1  F2  ...  Fn .
dt
Однако геометрическая сумма внутренних сил по третьему закону Ньютона
равна нулю. Отсюда
d
 m1v1  m2v2  ...  mnvn   F1  F2  ...  Fn ;
dt
mi vi  Pi – импульс i – го тела: поскольку
 Pi  P – есть импульс системы, то
i
dP
 F1  F2  ...  Fn .
dt
Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
В случае отсутствия внешних сил (система замкнута):
n
n
dP
d
   mi vi   0 , т. е. P   mi vi  const .
dt i 1 dt
i 1
Это и есть закон сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Всеобщность этого закона заключается в том, что он применим не только в
механике, но и для любых систем тел и любых процессов, происходящих с телами
системы, при единственном условии, чтобы на них не действовали внешние силы,
т. е. чтобы система была замкнута. Тогда импульс системы сохраняется неизменным, даже если тела системы разрушаются и в результате химических реакций из
одних веществ образуются другие и т. д. При этом, разумеется, обломки системы,
продукты химических реакций и пр. необходимо причислять к телам системы.
Если система состоит из одного тела, то для него закон сохранения импульса означает, что в отсутствие сил, на него действующих, импульс тела не меняется. Это равносильно закону инерции (скорость тела не меняется).
Применим закон сохранения импульса к задаче об отдаче орудия при выстреле. До выстрела орудие массой M и снаряд массой m покоятся. Значит, суммарный импульс системы равен нулю MV0  mv0  0 . После выстрела орудие и снаряд получат скорости, V и v . В силу закона сохранения импульса суммарный импульс системы после выстрела должен равняться нулю:
MV  mv  0  V  v
40
m
.
M
Значит, орудие получит скорость во столько раз меньшую скорости снаряда,
во сколько раз масса орудия больше массы снаряда. Различие знаков указывает на
противоположное направление скоростей орудия и снаряда.
Задачу удалось решить, не выясняя даже, какие силы и в течение какого
времени действовали на тела системы.
Пример 1. На рельсах стоит платформа весом Р1  98000 Н . На платформе
закреплено орудие весом Р2  49000 Н , из которого производится выстрел вдоль
рельсов. Вес снаряда Р3  980 Н , его начальная скорость v0  500 м с . Определить
скорость vx платформы в первый момент после выстрела, если: 1) платформа стояла неподвижно; 2) платформа двигалась со скоростью v1  18 км ч и выстрел был
произведен в направлении ее движения; 3) платформа двигалась со скоростью
v1  18 км ч и выстрел был произведен в направлении, противоположном направлению ее движения.
Решение. При неподвижной платформе начальная скорость снаряда относительно земли, очевидно, равна ее скорости относительно орудия. На основании
закона сохранения импульса имеем:
 m1  m2  m3  v1  m3v0   m1  m2  vx ,
где m1 – масса платформы, m2 – масса орудия и m3 – масса снаряда. В рассматриваемом случае v1  0 . Значит,
vx  
m3v0
 3,33 м с  12 км ч.
m1  m2
Знак минус указывает на то, что если принять направление движения снаряда положительным, т. е. v0  0 , то vx  0 , следовательно, платформа начнет двигаться в направлении, противоположном направлению движения снаряда.
Если выстрел был произведен в направлении движения платформы, то
начальная скорость снаряда относительно земли равна v2  v0  v1 , и тогда закон сохранения импульса дает:  m1  m2  m3  v1  m3 (v0  v1 )   m1  m2  vx , откуда
vx 
 m 1 m2  m3 
v1  m3  v0  v1 
m1  m2
 6 км ч .
Отметим, что vx  0 , т. е. платформа продолжает двигаться в том же направлении, но с уменьшенной скоростью.
Если выстрел производится в направлении, противоположном направлению движения платформы, то при v0  0 имеем v1  0 . Тогда закон сохранения импульса дает:
  m1  m2  m3  v1  m3  v0  v1    m1  m2  vx ,
откуда vx 
  m1  m2  m3  v1  m3  v0  v1 
m1  m2
 30 км ч . Отметим, что направления
vx и v1 совпадают (vx  0; v1  0) , следовательно, платформа продолжает двигаться в
том же направлении, но с увеличенной скоростью.
41
Движение тел переменной массы
Второму закону Ньютона подчиняются движения любых тел при скорости
движения, много меньшей скорости света, в том числе и движение тел с переменной массой. Получим уравнение движения тела с переменной массой на примере
движения ракеты.
Если в момент времени t масса ракеты m0 , а ее скорость v , то по истечении
времени dt ее масса уменьшится на dm и станет равной m  m0  dm , а скорость станет
равной v  dv . Изменение импульса системы за отрезок времени dt составит:
dP  (m0  dm)  v  dv   dm  v  u    m0v 
  m  v  dv    m0  m   v  u    m0v.
Здесь u – скорость истечения газов относительно ракеты. Раскрывая скобки
и учитывая, что dmdv – малая величина более высокого порядка малости по сравнению с остальными членами, получаем
dP  mdv  udm .
Если на систему действуют внешние силы, то, согласно второму закону
Ньютона, dP  Fdt , поэтому Fdt  mdv  udm или m
dv
dm
.
  F u
dt
dt
Член u
dm
dt
называется реактивной силой Fp . Если вектор u противоположен по направлению
вектору v , то ракета ускоряется, а если совпадает с направлением вектора v ,
тормозится. Значит, уравнение ma  F  Fp есть уравнение движения тела переменной массы. Оно получено И. В. Мещерским.
Если на ракету не действуют внешние силы  F  0  , то при u  const (ракета
движется прямолинейно) имеем:
m
dv
dm
dm
 u
 v  u 
 u nm  C .
dt
dt
m
Постоянную интегрирования находим из начальных условий: при t  0 скорость v  0 и m  m0 (стартовая масса). Тогда C  u nm0 и v  u n
m0
.
m
Пример 2. В начальный момент времени ракета имеет массу вместе с горючим m0 , а ее скорость равна нулю. Затем она движется в отсутствие внешних сил,
испуская непрерывную струю газа со скоростью u , постоянной относительно ракеты. Найти скорость ракеты в момент, когда ее масса равна m .
Решение. До старта ракета покоится, и ее импульс равен нулю. В силу закона сохранения импульса через время t , когда масса ракеты станет равной
m  m0  dm , ее импульс (вместе с импульсом выбрасываемых газов) также будет
равен нулю:  m0  dm  dv   u  v  dm  0 . Здесь v  0 – скорость ракеты в начальный
42
момент времени. Отсюда dv  u
dm
dm
 u
. Интегрируя по скорости от 0 до v
m0  dm
m
v
m
dm
m
.
 v  u n
m
m
0
m0
и по массе от m0 до m , получим:  dv  u 
0
Пример 3. Ракета движется в отсутствие внешних сил с постоянным ускорением w , скорость истечения газа относительно ракеты постоянна и равна u .
Масса ракеты в начальный момент времени равна m0 . Найти закон изменения
массы ракеты со временем.
Решение. Изменение импульса системы «ракета + газы» в силу закона сохранения импульса равно нулю: dP  mdv  udm  0 . Здесь m – масса ракеты в произвольный момент времени t ; dv  wdt – изменение скорости ракеты; dm – масса
m
dm
wdt
dm
wt
выброшенных газов. Отсюда mwdt  udm 


   dt . Интегрируя,
m
u
u0
m0 m
wt

m
wt
получаем: n   . После потенциирования имеем: m  m0 e u .
m0
u
1.3.2. Физические понятия вращательного движения
Для того чтобы перейти к выводу других двух законов сохранения, потребуется ввести в рассмотрение новые физические величины, имеющие и важное
самостоятельное значение. Речь идет о моменте силы, моменте инерции тела, моменте импульса тела, работе, мощности, энергии.
Момент силы
Рассмотрим подробнее вращательное движение. Мы уже знаем, что причиной любого движения являются приложенные к телу силы. Для того чтобы вызвать вращение тела, к нему необходимо приложить силу F , на которую накладываются три условия (рис. 1.3.1): 1) сила должна действовать в плоскости, перпендикулярной оси вращения; 2) сила не должна проходить через ось вращения;
3) должна быть направлена под прямым углом к радиусу r , проведенному от оси
вращения к точке приложения силы. При этом действие силы тем значительнее,
чем дальше расположена точка ее приложения от оси вращения, т. е. действие силы можно характеризовать моментом силы.
Рис. 1.3.1
43
Моментом силы F относительно неподвижной точки O называется физическая величина, определяемая векторным произведением радиуса-вектора, проведенного из точки O в точку приложения силы, на силу F : M   rF  (рис. 1.3.2).
Рис. 1.3.2
Направление момента M определяется правилом правого винта при его
вращении от r к F . Модуль момента силы M  FrSin (  – угол между векторами r и F ), rSin  – кратчайшее расстояние между линией действия силы и
точкой O . Это расстояние называется плечом силы. Таким образом, модуль момента силы оказывается равным M  Fl .
Если на тело действуют несколько сил, то их моменты складываются с учетом знака, т. е. направления. Необходимое (но недостаточное) условие равновесия
тела – сумма моментов, действующих на тело сил, должна равняться нулю.
Момент инерции
Из сказанного ясно, что действие силы при вращательном движении зависит
от плеча силы. Аналогично этому и инерция вращающегося тела зависит от расположения его массы относительно оси вращения. Чем дальше от оси вращения
находится масса тела, тем больше его инерция.
Это обстоятельство хорошо иллюстрируется на приборе Обербека (рис. 1.3.3):
на блоке закреплены четыре спицы, по которым могут перемещаться грузы с массами
m . На блок намотана нить, к концу которой привязан груз m1 . Двигаясь вниз, груз m1
раскручивает блок (создает вращающий момент).
Рис. 1.3.3
44
Если грузы m находятся на спицах близко от оси вращения, то груз m1 движется быстро. Если грузы m передвинуть к концам спиц, то груз m будет опускаться медленнее. Скорость вращения блока в этом примере определяется инерцией блока.
Для количественной характеристики влияния инерции тела на его вращение
в физике вводится величина, называемая моментом инерции. Моментом инерции
материальной точки называется произведение массы этой точки на квадрат расстояния до оси вращения:
I i  mi ri 2 .
Для нахождения момента инерции тела его разделяют на элементарные
фрагменты с размерами, которыми можно пренебречь по сравнению с расстоянием до оси вращения, вычисляют моменты инерции этих фрагментов; момент
инерции всего тела находят суммированием моментов инерции составляющих тело фрагментов: I   I i   mi ri2  кг  м 2  .
i
i
Для тел правильной геометрической формы формулы для вычисления моментов инерции вывести несложно. В качестве примера найдем момент инерции
однородного сплошного цилиндра высотой h и радиусом R относительно его
геометрической оси. Разобьем цилиндр (рис. 1.3.4) на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и
внешним – r  dr .
Рис. 1.3.4
Момент инерции каждого полого цилиндра dI  r 2 dm (так как dr  r , считаем, что расстояние всех точек цилиндра от оси равно r ), где dm – масса всего
элементарного цилиндра; его объем равен 2 rhdr . Если  – плотность материала,
то dm   2 rhdr и dI  2 h r 3dr . Тогда момент инерции сплошного цилиндра
R
I   dI  2 h  r 3dr  0,5 hR 4  ,  R 2 h – объем цилиндра, его масса m   R 2 h , а зна0
чит, момент инерции равен I  0,5mR2 .
Для тел сложной формы момент инерции определяется опытным путем.
45
Пример 4. Определить момент инерции сплошного шара массой m  10 кг и
радиусом R  10 м относительно оси, проходящей через центр тяжести.
Решение. Выделим диск толщиной dh (рис. 1.3.5).
Рис. 1.3.5
Его можно рассматривать как цилиндр радиусом r и высотой dh с моментом инерции
mr 2
r 2  4
  r 2 dh 
r dh .
2
2
2
r 2  R 2  h 2 . Тогда
dI 
Из рисунка следует, что
R


I   dI    R 4  2 R 2 h 2  h 4 dh 
0
Заменяя  
8
 R5 .
15
m
m
2
, получим I  mR 2  0, 04 кг  м 2 .

4
5
V
 R3
3
Работа и мощность
Действие силы, вызывающей перемещение тела, к которому она приложена,
характеризуется особой величиной, называемой работой. Если тело движется
прямолинейно и на него действует постоянная сила F , направление которой составляет некоторый угол  с направлением перемещения r , то работа этой силы
равна ее скалярному произведению F на перемещение точки приложения силы:
A  F  r  F  r  Cos  Fr r .
Здесь Fr – проекция силы F на направление перемещения.
В общем случае сила может меняться как по модулю, так и по направлению,
поэтому последней формулой пользоваться нельзя (можно только при F  const ).
Но если рассмотреть элементарное перемещение dr , то силу F можно считать
постоянной, а движение точки ее приложения – прямолинейным. Тогда элементарной работой силы F на перемещении dr будет называться величина
dA  F  dr  F  dr  Cos  Fr  dr ,
где  – угол между векторами F и dr .
Работа силы на участке траектории от 1 до 2 равна алгебраической сумме
элементарных работ на отдельных бесконечно малых перемещениях:
2
2
1
1
A   FCos
 dri   FCos dr   Fr dr .
i
i
46
Из приведенных формул для работы видно, что при  
ложительна; при  

2
– работа силы отрицательна; при  

2

2
работа силы по-
(сила перпендику-
лярна перемещению) – работа равна нулю.
В системе СИ единицей работы является Джоуль: 1 Дж – это работа, совершаемая силой в 1 Н на пути 1м.
Чтобы характеризовать скорость совершения работы вводят понятие мощности, т. к. мощность характеризует количество работы, совершенное в единицу
времени:
N
dA
.
dt
Если работа совершается равномерно   const  , то мощность измеряется
 dt

отношением работы A , совершенной за время t , к величине этого промежутка
времени:
dA
N
A
.
t
Так как при этом A  F  r  Cos (работа совершается равномерно силой,
направление которой составляет угол  с перемещением), то
N
F  r  Cos
 FvCos  Fv ,
t
т. е. мощность равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.
Мощность в системе СИ измеряется в ваттах. 1 Вт – это мощность, при которой работа в 1 Дж совершается за 1с.
Пример 5. Вратарь, бросая мяч, действует на него с постоянной силой в течение 0,1 с . Рука его движется вперед на расстояние 1 м . Масса мяча 600 г . Определить ускорение мяча. Какая сила действует на мяч? Найти среднюю мощность,
развиваемую вратарем.
Решение. Под действием постоянной силы, т. е. с постоянным ускорением мяч
движется на расстоянии s  1 м в течение t  0,1 c . Значит, s 
at 2
2s
м
 a  2  200 2 . По
2
t
с
второму закону Ньютона F  ma  120 H . Работа, совершенная этой силой, равна
A  Fs  120 Дж . Развиваемая мощность N  A t  1200 Вт .
Энергия
Некоторые механизмы способны «запасать» работу, т. е. накапливать способность совершать работу. Удобным примером являются часы: поднятая гиря (в
гиревом механизме) или сжатая пружина могут приводить в движение детали часов, совершая работу против сил трения. При этом работа производится при изменении состояния тела: при опускании гири, раскручивании сжатой пружины
и т. п. В связи с этим в физике введено понятие энергии как величины, характери47
зующей способность тел при переходе из одного состояния в другое совершать
определенную работу. Таким образом, энергия определяет запас работы, которую
может совершить тело, изменяя свое состояние. Энергия и работа измеряются в
одних единицах.
Известно, что взаимное превращение различных конкретных форм движения
материи (механической, тепловой, электрической и т. п.) происходит в строго определенных количественных соотношениях. Это требует установления общей меры для
всех превращений. Такой мерой является энергия. Носители энергии – только материальные объекты, и независимо от них энергия рассматриваться не может.
Различают два вида механической энергии: кинетическую и потенциальную.
Кинетическая энергия – это энергия механического движения тела. Сила F , действуя
на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы
F на пути, который тело прошло за время возрастания скорости от 0 до dv , идет на
увеличение кинетической энергии dЕк тела: dA  dЕк . По второму закону Ньютона
dv
. Умножая обе части этого равенства на перемещение
dt
dv
dr
, то dA  mvdv  mvdv  dЕк . Отсюда
Fdr  m
dr  dA . Так как v 
dt
dt
v
mv 2
Ек   mvdv 
.
2
0
F m
dr , получим
Тело массой m, движущееся со скоростью v , обладает кинетической энергией Ек 
mv 2
. Если на движущееся со скоростью v тело начнет действовать сила
2
против его движения, то тело будет замедлять свое движение и остановится, произведя работу против действующей силы. Работа будет совершена за счет кинетической энергии тела.
Потенциальная энергия связана с взаимодействием тел (или частей одного и
того же тела). Это взаимодействие осуществляется через посредство того или
иного силового поля: гравитационного, поля молекулярных сил, электростатического и т. п. Если силовое поле характеризуется тем, что работа, совершаемая силами поля при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений тела, то такое поле называется потенциальным, а силы поля – консервативными.
Докажем, что сила тяжести является консервативной. Эта сила в любой точке
имеет одинаковую величину и одинаковое направление – вниз по вертикали (рис. 1.3.6).
48
Рис. 1.3.6
Поэтому независимо от того, по какому из путей (1 или 2) движется частица,
работа А12 будет равна
A12  mg  s12  mg  s12Cos  mg  ( s12 ) g .
Здесь  – угол между направлениями перемещения и действия силы тяжести;
 s12  g – проекция вектора s12 на направление вектора g . Очевидно, что  s12  g  h1  h2 ,
где h1 , h2 – высоты начального и конечного положений точки. Следовательно, выражение для работы можно записать в виде: A12  mg  h1  h2  . Это выражение, очевидно,
не зависит от пути. Отсюда следует, что сила тяжести консервативна.
Если работа, совершаемая силой, зависит от траектории перемещения тела из
одной точки в другую, такая сила называется диссипативной. Ее примером является
сила трения.
Для перемещения тела в силовом поле против действия сил поля необходимо совершить работу с помощью внешней силы. Эта работа пойдет на увеличение
потенциальной энергии тела. И, наоборот, само тело, перемещаясь под действием
сил поля, может совершить работу; при этом его потенциальная энергия соответственно уменьшится, т. е. работа сил поля будет равна приращению потенциальной энергии тела, взятому со знаком минус: dA  dЕП . В обоих случаях значение
имеет разность величин потенциальных энергий в начальном и конечном положениях тела. Поэтому потенциальную энергию тела определяют не по абсолютной
величине, а по отношению к величине, условно принятой за нулевой уровень.
Например, потенциальную энергию тела в поле земного тяготения определяют
сравнительно с энергией, которую оно имеет на поверхности Земли (на уровне
моря). В этом случае потенциальная энергия ЕП тела измеряется произведением
силы тяжести P на его высоту h над уровнем моря:
ЕП  Ph  mgh .
Это выражение для потенциальной энергии тела в поле сил земного тяготения
вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия отрицательной быть не может). Если принять за нуль потенциальную энергию тела, лежащего на поверхности
Земли, то потенциальная энергия тела, находящегося на дне шахты глубиной h , будет равна ЕП  mgh .
49
1.3.3. Закон сохранения полной механической энергии
Полная механическая энергия – это сумма энергии механического движения
и энергии взаимодействия: E  Ек  ЕП . Для доказательства закона сохранения этой
энергии рассмотрим систему материальных точек массами m1 ,..., mn , движущихся
со скоростями v1 ,..., vn . Пусть F1,..., Fn - равнодействующие внутренних консервативных сил, действующих на каждую из этих точек. Через F1 ,..., Fn обозначим равнодействующие внешних сил, которые также будем считать консервативными.
Кроме того, будем считать, что на материальные точки действуют еще и внешние
неконсервативные силы, равнодействующие которых обозначим через f1 ,..., f n .
По второму закону Ньютона
dv1
 F1  F1  f1 ,
dt
..................................
dv
mn n  Fn  Fn  f n .
dt
m1
Двигаясь под действием этих сил, точки системы за интервал времени dt совершат перемещения dr1 ,..., drn , причем dri  vi dt . Умножив каждое из уравнений
движения на соответствующее перемещение, получим:
m1  v1dv1    F1  F1  dr1  f1dr1 ,
.............................................
mn  vn dvn    Fn  Fn  drn  f n drn .
После сложения всех уравнений получим:
n
n
i 1
i 1
 mi  vi dvi    Fi Fi 
n
dri   fi dri .
i 1
Первый член в левой части:
 mi vi2 
  dЕ к
 mi vi dvi    d 

i 1
i 1  2 
n
n
есть приращение кинетической энергии системы. Второй член
  Fi Fi 
dri
равен элементарной работе внутренних и внешних консервативных сил, взятой со
знаком минус, т. е. равен элементарному приращению потенциальной энергии системы dEП. Правая часть задает работу внешних неконсервативных сил. Таким образом, имеем
d  Ек  ЕП   dA .
При переходе системы из состояния 1 в состояние 2:
2
 d  Ек  ЕП   A12 , т. е.
1
изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершаемой при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то
50
d  Ек  Еn   0  Ек  Еn  E  const ,
т. е. полная механическая энергия системы сохраняется. Это и есть закон сохранения механической энергии системы: в системе тел,
между которыми действуют только консервативные силы, полная механическая
энергия сохраняется, т. е. со временем не изменяется.
Если неконсервативные силы присутствуют, то механическая энергия системы постепенно уменьшается за счет преобразования ее в другие виды энергии
(неконсервативными силами совершается работа). Кроме механической энергии
тело или система тел обладает внутренней энергией, к которой относятся кинетическая энергия теплового движения молекул, потенциальная энергия их взаимодействия, энергия, связанная с движением электронов в атомах и т. д. Сумма механической и внутренней энергий называется полной энергией тела.
Для всех видов энергии возможен переход из одного вида в другой. Опытным фактом является то, что все виды энергии могут взаимно превращаться, однако, это может происходить только при условии, что полная энергия тела остается неизменной. Энергия никогда не исчезает и не появляется вновь, она лишь переходит из одного вида в другой. В этом заключается физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее
движения.
Пример 6. Скорость реактивного самолета на некотором участке меняется с
расстоянием по закону: v  D  Bs . Найти работу за промежуток времени  t1 , t2  , если масса самолета m . В момент времени t1 скорость равна v1 .
Решение. Ускорение самолета a 
dv
ds
 B  Bv .
dt
dt
Разделив переменные, полу-
dv
 Bdt . После интегрирования и потенцирования последнего выражения
v
получим, что скорость в момент времени t 2 равна v2  v1e Bt2 t1  . Работа равна разно-
чим:
mv22 mv12 mv12  2 Bt2 t1  


e
1 .
сти кинетических энергий A 

2
2
2 
Пример 7. Необходимо вывести выражения для скоростей двух тел после
их центрального абсолютно упругого соударения.
Решение. Центральным называется удар, если тела до удара движутся вдоль
прямой, проходящей через их центры масс. При абсолютно упругом ударе в обоих телах не остается никаких деформаций, и вся кинетическая энергия, которой
обладали тела до удара, снова превращается в кинетическую энергию. При таком
соударении выполняются законы сохранения импульса и кинетической энергии.
Обозначим скорости двух тел с массами m1 и m2 до удара через v1 и v2 , после удара – через v1 и v2 . При прямом центральном ударе векторы скоростей тел
до и после удара лежат на прямой, соединяющей их центры. Проекции векторов
скорости на эту линию равны модулям скоростей. Запишем законы сохранения:
 закон сохранения импульса m1v1  m2v2  m1v1  m2v2 ;

2
2
2
2
закон сохранения энергии m1v1  m2v2  m1v1  m2v2 .
2
2
После простых преобразований получаем:
51
2
2
m1  v1  v1   m2  v2  v2  ;



(*)

m1 v12  v12  m2 v22  v22 .
Поделив почленно второе на первое, получим: v1  v1  v2  v2 . Выражая отсюда v 2 и подставляя в формулу (*), имеем:
v1 
v2 
 m1  m2 
v1  2m2 v2
,
m1  m2
 m2  m1 
v2  2m1v1
.
m1  m2
Пример 8. Необходимо получить выражения для скорости тел после их
центрального неупругого соударения.
Решение. Неупругий удар – столкновение двух тел, в результате которого
тела объединяются, дальше двигаясь как единое целое. Пусть массы тел m1 и m2 ,
их скорости до удара v1 и v2 . По закону сохранения импульса m1v1  m2v2   m1  m2  v .
Отсюда
v
m1v1  m2 v2
m1  m2
. Если тела двигались навстречу друг другу, то они будут
продолжать двигаться в ту сторону, в которую двигалось тело с большим импульсом. При неупругом ударе часть кинетической энергии тел переходит в тепловую
энергию, поэтому закон сохранения энергии не выполняется.
1.3.4. Основное уравнение динамики вращательного движения
Введем понятие абсолютно твердого тела и выведем формулу для кинетической энергии тела при вращательном движении. Абсолютно твердое тело – это
тело, которое ни при каких условиях не может деформироваться, и при всех условиях расстояние между двумя точками остается постоянным.
Разобьем вращающееся абсолютно твердое тело на элементарные объемы с
массами m1 ,..., mn , расположенные на расстояниях r1 ,..., rn от оси вращения. Кинетическая энергия вращающегося тела будет равна сумме энергий элементарных
объемов:
Евр 
m v2 n m v2
m1v12
 ...  n n   i i .
2
2
2
i 1
Так как тело абсолютно твердое, угловая скорость всех элементарных объемов одинакова:  
v
v1
 ...  n . Заменив vi  ri , получим
r1
rn
mi 2 2  2 n
I 2
.
ri 
mi ri 2 

2
2 i 1
2
i 1
n
Евр  
52
В случае плоского движения тела (цилиндр катится без скольжения)
Ек 
mv 2 I  2

2
2
: кинетическая энергия равна сумме энергий поступательного и вра-
щательного движений.
Используя выражение для кинетической энергии вращающегося тела, выведем основное уравнение вращательного движения. Работа силы F (рис. 1.3.7),
приложенной к телу в точке B , находящейся на расстоянии r от оси вращения,
при повороте тела на угол d будет равна: dA  FSin  r  d (  – угол между
направлением силы и радиус-вектором r ; при повороте на бесконечно малый
угол d точка приложения силы B проходит путь ds  rd ). Так как rSin  l и
Fl  M – момент силы относительно точки 0, имеем dA  Md . Работа при вращении
тела идет на увеличение его кинетической энергии dA  dЕк . Но
 I 2 
d
d
d
. А 
, значит,
 I
dЕк  d 
  I d . Отсюда Md  I  d  или M
dt
dt
dt
2


d
. Производная от угловой скорости по времени есть угловое ускорение  .
M I
dt
Окончательно: M  I .
Рис. 1.3.7
Последнее равенство называется основным уравнением динамики вращательного движения твердого тела. Собственно это аналог второго закона Ньютона
для вращательного движения: роль силы играет момент силы, роль массы – момент инерции; роль ускорения – угловое ускорение.
Пример 9. С одного уровня наклонной плоскости одновременно начинают
скатываться без скольжения сплошные цилиндр и шар одинаковых масс и одинаковых радиусов. Определить: 1) отношение скоростей цилиндра и шара на данном
уровне; 2) их отношение в данный момент времени.
Решение. Кинетическая энергия тела, катящегося без скольжения, равна
Ек 
mv 2 I  2

. Здесь m – масса тела, v – скорость центра масс, I – момент инер2
2
ции тела,  – угловая скорость вращения.
Для цилиндра: Ек 
mvц2

I цц2

mvц2

mr 2 vц2
2
2
2
2  2r
2 2
mv
2mr vш 7

 mvш2 .
Для шара: Ек 
2
2
5  2r
10
2

3 2
mvц .
4
2
ш
По условию цилиндр и шар переместились на одинаковые расстояния по
высоте. Значит, их потенциальные энергии изменились на одинаковую величину:
53
ЕП  mgh , где h – расстояние по вертикали, на которое спустились цилиндр и шар.
В силу закона сохранения механической энергии Т  П .
Для цилиндра: 3 mvц2  mgh  vц  4 gh .
4
3
Для шара: 7 mvш2  mgh  vш  10 gh .
10
7
Отсюда имеем:
vц
vш

14
15
.
Во втором случае цилиндр и шар перемещались за одинаковый промежуток
времени. Движение обоих тел равноускоренное. Путь, пройденный ими, равен:
at 2 vt
 . Расстояние по вертикали,
2
2
h  sSin  0,5vtSin , где  – угол наклона
s
на которое опустились тела, равно
плоскости. Значит, потенциальная энергия изменилась на величину ЕП  mgh  0,5mgvtSin . Изменение потенциальной
энергии равно изменению кинетической энергии.
3 2 1
2
mvц  mgvц tSin  vц  gtSin .
4
2
3
7
1
5
mvш2  mgvшtSin  vш  gtSin .
10
2
7
Для цилиндра имеем:
Для шара:
Отсюда
vц
vш

14
.
15
1.3.5. Закон сохранения момента импульса
Продолжая аналогию, можно сказать, что аналогом импульса тела при вращательном движении является момент импульса относительно оси вращения.
Пусть точка А имеет импульс P  mv (рис. 1.3.8). Моментом импульса материальной точки A относительно неподвижной точки O называется физическая величина, определяемая векторным произведением L   rP    rmv  . Здесь r – радиусвектор точки A , P  mv – импульс точки A . Направление вектора L определяется
правилом правого винта. Модуль момента импульса L  rPSin  mvrSin  Pl .
Рис. 1.3.8
При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности радиуса ri с некоторой скоростью vi .
54
Скорость vi и импульс mi vi перпендикулярны радиусу-вектору ri , т. е. радиус является плечом вектора mv . Значит Li  mi vi ri . В этом случае момент импульса всего
n
тела L   mi vi ri . Так как vi   ri , получаем
i 1
n
n
i 1
i 1
L   mi ri 2    mi ri 2  I  .
Момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Дифференцируем последнее равенство по времени:
dL
d
I
 I  M
dt
dt
.
Это еще одна форма основного уравнения динамики вращательного движения.
Момент силы и момент импульса направлены одинаково, поэтому можно записать
dL
M.
dt
В замкнутой системе момент внешних сил равен нулю M  0 . Отсюда
dL
 0  L  const  I   const .
dt
Это и есть закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется со временем.
Если в этих условиях ( M  0 ) изменяется момент инерции тела, то в силу
неизменности произведения I изменяется угловая скорость. Этим обстоятельством широко пользуются спортсмены: акробаты, прыгуны в воду и т. д.
Пример 10. Маховое колесо, имеющее момент инерции I  245 кг  м 2 , вращается, делая n  20 об с . Через t  1 мин , после того как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2)
число оборотов, которое сделало колесо до полной остановки после прекращения
действия сил.
Решение. После прекращения действия вращающего момента на вращение
колеса влияет только сила трения. Она постоянна, поэтому вращение равнозамедленное. Угловое ускорение будет равно  
k  н
t
. Конечное значение угловой
скорости k  0 , так как колесо остановилось. Поскольку 1 об / с  2 рад / с , то
2 n
. Используя основной закон вращательного движения, поt
2 nI
M  I 
 512,9 Н  м . Для нахождения числа оборотов учтем, что
t
н  2 n рад / с и  
лучаем:
полный угол поворота колеса при равнозамедленном вращении равен
  нt 
t2
2
 2 nt   nt   nt  3774 рад .
Отсюда число оборотов до полной остановки составит N 
55

 601 об .
2
Пример 11. Две гири разного веса соединены нитью и перекинуты через
блок, момент инерции которого I  50 кг  м 2 и радиус R  20 см . Блок вращается с
трением, и момент сил трения равен М тр  98,1 Н  м . Найти разность натяжений
нитей Т 2  Т1 по обе стороны блока, если известно, что блок вращается с постоянным угловым ускорением   2,36 рад с 2 .
Решение. Момент сил трения и вращающий момент противодействуют друг
другу, поэтому результирующий момент равен их разности: M  T2  T1  R  M тр .
Отсюда, по основному уравнению динамики вращательного движения, имеем:
M  I   T2  T1 
I   M тр
R

50  2,36  98,1
 1080,5 ( H ) .
0.2
1.4. Колебательное движение
Колебаниями называются процессы, отличающиеся той или иной степенью
повторяемости. Примерами колебаний могут служить колебания маятника часов,
колебания струны и т. д. Рассмотрим самые распространенные в природе колебания – механические.
Колебания называются свободными или собственными, если они совершаются
за счет первоначально сообщенной энергии при последующем отсутствии внешних
воздействий на колебательную систему. Примером свободных колебаний могут
служить колебания шарика, подвешенного на нити. Для того чтобы вызвать колебания, можно либо толкнуть шарик, либо, отведя его в сторону, отпустить.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером могут служить колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.
1.4.1. Гармонические колебания
Простейшими колебаниями являются гармонические колебания, т. е. колебания, при которых колеблющаяся величина изменяется со временем по закону
синуса или косинуса. Рассмотрение гармонических колебаний важно по двум
причинам: а) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; б) различные периодические процессы с иной зависимостью от времени могут быть представлены как наложение нескольких гармонических колебаний.
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси x около положения равновесия, принятого за начало координат.
Зависимость координаты x от времени t опишется выражением x  ACos(0t   ) ,
где A – максимальное значение колеблющейся величины, называемое амплитудой колебаний; 0 – круговая (циклическая) частота;  – начальная фаза колебаний (фаза в момент времени t  0 ); 0t    – фаза колебаний в момент времени t .
56
Поскольку косинус – периодическая функция с периодом 2 , то колеблющаяся величина будет принимать одинаковые значения через такой промежуток
времени Т , за который фаза колебаний получает приращение 2 . Этот промежуток времени называется периодом. По определению 0  t  T      0t     2 ,
значит, T  2 0 .
Число колебаний в единицу времени называется частотой колебания  .
Очевидно, что частота обратна периоду   1 T . За единицу частоты принимается
герц – частота такого колебания, период которого равен 1с.
Из выражения для периода следует 0  2 Т , т. е. 0 дает число колебаний
за 2 секунд. Поэтому эта величина называется круговой или циклической частотой; с обычной частотой она связана соотношением 0  2 .
Дифференцирование величины x по времени один и два раза дает выражения для ее скорости и ускорения:
dx dt  v   A0 Sin 0t     A0Cos 0t     2 ,
d 2 x dt 2  a   A02Cos 0t     A02Cos 0t      .
Из выражения для ускорения следует, что сила, действующая на колеблющуюся точку массой m , равна F  ma  mA02Cos 0t     m02 x , т. е. сила пропорциональна смещению и направлена в противоположную сторону (к положению
равновесия). Из того же выражения следует дифференциальное уравнение гармонических колебаний: a  x; ACos 0t     x  x  02 x  0 , решением которого является выражение x  ACos 0t    .
Выражения для кинетической и потенциальной энергии принимают вид:
T
x
mv 2 mA202

Sin 2 0t    ,
2
2
U    Fdx 
0
m02 x 2 mA202

Cos 2 0t    .
2
2
Отсюда полная механическая энергия получается равной E  T  U 
mA202
.
2
Пример 1. Точка колеблется гармонически по закону x  x0 Sin t    . Найти
максимальные значения скорости и ускорения.
Решение. Выражения для скорости и ускорения находятся дифференцированием закона колебаний по времени, соответственно, один и два раза:
v
d 2 x dv
dx
  x0 2 Sin t    .
 x0 Cos t    ; a  2 
dt
dt
dt
Скорость примет максимальное значение v  x0 , когда Cos t     1 .
Ускорение примет максимальное значение a  x0 2 , когда Sin t     1 .
Пример 2. Определить отношение потенциальной энергии гармонически
колеблющейся точки к ее кинетической энергии, если известна фаза колебаний.
57
Решение. Выражения для кинетической и потенциальной энергий гармонически колеблющейся точки имеют вид:
T
mv 2 mA202

Sin 2 0t    ,
2
2
x
U    Fdx 
0
m02 x 2 mA202

Cos 2 0t    .
2
2
Отсюда для отношения энергий получаем:
U
 tg 2 t    .
T
Примеры гармонических колебаний
Система, совершающая колебания, описываемые уравнением вида x  02 x  0 ,
называется гармоническим осциллятором. Примерами гармонического осциллятора являются пружинный, физический и математический маятники.
Пружинный маятник – это груз, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы
F  kx , где k – жесткость пружины. По второму закону Ньютона mx  kx или
x
k
k
x  0 . Обозначив
 02 , можем записать: x  02 x  0 , т. е. пружинный маятник
m
m
действительно совершает гармонические колебания по закону: x  ACos 0t   с
циклической частотой 0  k m и периодом T  2 m k .
Потенциальная энергия пружинного маятника равна работе упругой силы,
x
взятой со знаком минус: U   dA    kx  dx  kx 2 2 .
0
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Отклонение маятника от положения равновесия характеризуется углом  , образованным нитью с вертикалью (рис. 1.4.1). При отклонении маятника от положения равновесия возникает вращающий момент M , равный по величине mglSin . Этот момент стремится вернуть маятник в положение
равновесия, т. е. действует аналогично упругой силе. Поэтому углу отклонения 
и моменту M следует приписывать противоположные знаки. (Это можно обосновать, и используя правило правого винта.) Таким образом, выражение для вращательного момента имеет вид M  mglSin .
58
Рис. 1.4.1
Используя выражение для момента инерции маятника  I  ml 2  и основное
уравнение динамики вращательного движения
 M  I  , можно записать:
g
Sin  0 .
l
Sin   . Введя
ml 2  mglSin . Поделив это уравнение на ml 2 , приведем его к виду  
Если ограничиться рассмотрением малых колебаний, то можно
обозначение g l  02 , получим   02  0 , т. е. малые колебания математического
маятника есть гармонические колебания, совершающиеся по закону
  АCos 0t  0  с периодом T  2 0  2
l
.
g
Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении маятника от положения равновесия на угол  (рис. 1.4.2) возникает вращающий момент, стремящийся вернуть
маятник в положение равновесия. Этот момент равен M  mglSin , где m – масса
маятника, l – расстояние между точкой подвеса и центром масс С маятника. Обозначив момент инерции маятника относительно оси, проходящей через точку
подвеса, буквой I , можно записать: I  mglSin . В случае малых колебаний это
выражение переходит в уже известное нам уравнение:   02  0 . Здесь через 02
обозначена величина 02  mgl I . Отсюда следует, что малые колебания физического маятника являются гармоническими колебаниями, частота которых зависит
от массы маятника, момента инерции маятника относительно оси вращения и расстояния от оси вращения до центра масс маятника. Период колебаний физического маятника определяется выражением T  2 I  mgl  . Из сравнения этого выражения с периодом колебаний математического маятника легко заключить, что
данный физический маятник колеблется с таким же периодом, как и математический маятник длиной L 
I
. Эту длину называют приведенной длиной физичеml
ского маятника.
Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом
данного физического маятника.
59
Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на
расстоянии приведенной длины от оси вращения, называется центром качания
физического маятника (точка О на рис. 1.4.2).
Рис. 1.4.2
Нетрудно показать, что при подвешивании маятника в центре качания О
приведенная длина, а значит, и период колебаний будут теми же, что и в начале.
Следовательно, точка подвеса и центр качания обладают свойством взаимности:
при переносе точки подвеса в центр качания прежняя точка подвеса становится
новым центром качания.
Пример 3. Определить натяжение нити в момент t , если математический
маятник массой m , длиной l совершает гармонические колебания по заданному
закону   0 Sin t    .
Решение. Маятник движется по дуге окружности (рис. 1.4.3) радиуса l , и
сила натяжения нити в произвольный момент времени будет равна сумме составляющей силы тяжести по направлению нити и центростремительной силы, создающей нормальное ускорение: Fн 
mg
mv 2

.
Cos
l
Рис. 1.4.3
Мгновенная скорость в этот момент времени равна v  l
d
 l 0 Cos t    .
dt
Следовательно, выражение для силы натяжения принимает вид:
Fн 
mg
 ml 02 2Cos 2 t    .
Cos  0 Sin t    
Пример 4. Физический маятник представляет собой тонкий однородный
стержень длиной L  25 см . Определить, на каком расстоянии от центра масс
должна быть точка подвеса, чтобы частота колебаний была максимальна.
60
Решение. Период колебаний физического маятника равен T  2
стота обратна периоду:   1  1
T
2
I
. Чаmgl
mgl
. Здесь l – расстояние от точки подвеса до
I
центра масс; m – масса стержня; I – момент инерции стержня относительно точки подвеса. По теореме Штейнера, I  I c  ml 2 . Здесь I c 
стержня относительно центра масс. Отсюда  
1
2
1
mL2
12
– момент инерции
mgl
mL 12  ml 2
2
. Экстремальные
значения частоты достигаются при таких значениях l , при которых
d
 0 . Дифdl
ференцируем полученное выражение и приравниваем его нулю:
d
g

dl 2


2
2
2
L2  12l 2 12 L  12l  284l
0.
2
12l
L2  12l 2


Из трех сомножителей равным нулю может быть только третий. Отсюда
12  L  12l 2   284l 2  0  l  7,3 см . При полученном значении l будет достигаться
2
максимум частоты, если вторая производная d 2 dl 2  0 . В этом можно убедиться,
выполнив дифференцирование и подставив числовые значения.
Пример 5. При подвешивании грузов массами m1  500 г и m2  400 г к свободным пружинам последние удлинились одинаково ( l  15 см ). Пренебрегая массой пружин, определить: 1) периоды колебаний грузов; 2) какой из грузов при
одинаковых амплитудах обладает большей энергией и во сколько раз?
Решение. Упругая сила F пропорциональна удлинению пружин: F  kl ,
где k – жесткость пружины. Знак минус означает, что сила и удлинение направлены противоположно. В нашем случае пружины растягиваются силами F  mg .
Значит, для первой пружины k1  m1 g l , для второй – k2  m2 g l . Поскольку период
колебаний пружинного маятника равен T  2 m k , то ясно, что периоды колебаний обоих маятников одинаковы:
T  2 m1 k1  2 m2 k2  2 l g  0, 78 с .
Потенциальная энергия пружинного маятника П 
жесткости
пружины.
Значит,
более
жесткая
k1 k2  m1 m2  1, 25 раз большую потенциальную энергию.
kl 2
2
пропорциональна
пружина
имеет
в
1.4.2. Затухающие колебания
Во всякой реальной колебательной системе имеются силы сопротивления,
действие которых приводит к уменьшению энергии системы. Если энергия не
восполняется за счет работы внешних сил, колебания будут затухать. В простей61
шем и вместе с тем наиболее часто встречающемся случае сила сопротивления F *
пропорциональна величине скорости: F *  rx , где r – постоянная, называемая
коэффициентом сопротивления. Знак минус обусловлен тем, что сила F * и скорость v имеют противоположные направления, следовательно, их проекции на
ось x имеют разные знаки.
Уравнение второго закона Ньютона при наличии сил сопротивления имеет
вид: mx  kx  rx . Обозначив
r
k
 2 и
 02 , перепишем последнее уравнение в
m
m
ином виде: x  2 x  02 x  0 . Это дифференциальное уравнение описывает затухающие колебания системы. Величина  0 представляет собой ту частоту, с которой
совершались бы свободные колебания системы в отсутствие сопротивления среды, т. е. при r  0 . Эту частоту называют собственной частотой системы.
Решение уравнения затухающих колебаний найдем в виде x  e   t  u , где
u  u (t ) . Произведя подстановку, получим: u  02   2  u  0 . При небольшом затухании    0  имеем:  2  02   2  u   2u  0 ; решением этого уравнения является функция u  A0Cos t    . Таким образом, в случае малых затуханий
  2  02  колеблющаяся величина изменяется по закону: x  A0etCos t    .
Здесь A  A0 e   t – амплитуда затухающих колебаний; A0 – начальная амплитуда.
Скорость затухания колебаний определяется величиной  
называют коэффициентом затухания. Промежуток времени  
1

r
, которую
2m
, в течение кото-
рого амплитуда уменьшается в e раз, называется временем релаксации. Следовательно, коэффициент затухания обратен времени релаксации.
Затухание нарушает периодичность колебаний и, строго говоря, понятие
периода к затухающим колебаниям неприменимо. Но при малом затухании
условно пользуются понятием периода как промежутка времени между двумя последующими максимумами или минимумами колеблющейся величины и полагают T  2   2 02   2 (рис. 1.4.4).
Рис. 1.4.4
62
Если A  t  и A  t  T  – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
  t T
A  t  A  t  T   A0e   t A0e    e  T называется декрементом затухания, а его логарифм   ln
A t 
T
1
 Т  
A t  T 
 Ne
– логарифмическим декрементом затухания; Ne
– число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная величина для данной колебательной системы.
Для характеристики колебательной системы также употребляется величина
Q      Ne , называемая добротностью колебательной системы. Как видно из
определения, добротность пропорциональна числу колебаний Ne , совершаемых
системой за время  , за которое амплитуда колебаний уменьшается в е раз.
Пример 6. Логарифмический декремент затухания математического маятника равен   0, 2 . Найти, во сколько раз уменьшится амплитуда колебаний за
одно полное колебание маятника.
Решение. Для амплитуд последовательных затухающих колебаний имеем:
A1  A0 e

t
T
и A2  A0 e

t T
T
. Отсюда
A1
 e   e0,2  1, 22 .
A2
1.4.3. Вынужденные колебания
До сих пор мы рассматривали свободные (или собственные) колебания: выведенная из положения равновесия или получившая толчок система совершает
колебания, будучи предоставленной самой себе. Теперь пусть колебательная система подвергается действию внешней силы, изменяющейся по гармоническому
закону: Fx  F0Cost . Уравнение второго закона Ньютона в этом случае имеет вид:
r
k
; 02  , перепишем уравнение
m
m
F
следующим образом: x  2 x  02 x  f 0Cost , где f 0  0 . Это уравнение описывает
m
mx  kx  rx  F0Cost . Введя обозначения 2  
вынужденные колебания.
В теории дифференциальных уравнений доказывается, что решение этого
уравнения равно сумме общего решения однородного уравнения (которое мы
только что получили для затухающих колебаний) и частного решения неоднородного уравнения, т. е. решения, не содержащего постоянных. Частное решение легче найти в комплексной форме. (Есть такой прием решения дифференциальных
уравнений: если в решаемом уравнении правая часть вещественная, то к ней прибавляют произвольную мнимую функцию и ищут комплексное решение уравнения. Найдя это комплексное решение, берут его вещественную часть. Она и будет
представлять собой решение исходного уравнения.) Найденное таким способом
63
частное решение уравнения имеет вид: x  ACos t    , где A 
f0

2
0
и   arctg
2 
, т. е. x 
02   2
f0

2
0


2 2
 2

2
 4 2 2

2 
Cos  t  arctg 2
.

2 
2 2
0

 4 
Общее
решение однородного уравнения было получено ранее:
x1  A0e Cos 1t  1  ( А0 и 1 – произвольные постоянные). Общее решение неоднородного уравнения равно сумме  x  x1  . Слагаемое x1 играет роль только в
начальной стадии процесса (при увеличении t множитель e   t стремится к нулю)
до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, равного А . Графический вид вынужденных колебаний представлен на рис. 1.4.5. В
установившемся режиме вынужденные колебания происходят с частотой  и являются гармоническими. Амплитуда и фаза колебаний зависят от частоты.
t
Рис. 1.4.5
Из выражения для амплитуды А видно, что оно имеет экстремальный характер: при некотором значении частоты  амплитуда достигает максимума. Это
значение частоты называется резонансной частотой. Чтобы найти его, необходимо найти максимум выражения для амплитуды (амплитуда максимальна, если
знаменатель выражения минимален). Продифференцировав подкоренное выражение в знаменателе и приравняв производную нулю, получим условие, определяющее значение резонансной частоты:

d  2
0   2


d

2


 4 2 2   4 02   2   8 2  0 .

Корни этого уравнения   0;  02  2 2 ; из этих корней только положительный имеет физический смысл. Следовательно, резонансная частота равна
 рез  02  2 2 . Явление резкого возрастания амплитуды вынужденных колебаний
при приближении частоты вынуждающей силы к частоте  рез называется резонансом. Для значения резонансной амплитуды имеем Арез 
f0
2 02   2
.
Пример 7. На тело действует сила, изменяющаяся по закону F  ACost ( A
и  – постоянные числа). Найти закон движения тела при условии, что при t  0 ,
64
x  0 и v  0 . Установить, что такое движение является колебательным. Опреде-
лить период колебания, наибольшее значение смещения и наибольшее значение
скорости.
Решение. По второму закону Ньютона
dv F
 .
dt m
Так как F  ACost , то
dv A
A
Интегрируя последнее уравнение, получаем:
 Cost  dv  Costdt .
dt m
m
A
dx
, то
v
Sint . Постоянная интегрирования равна нулю. Поскольку v 
m
dt
A
A
dx 
Sintdt  x  
Cost . Из последнего уравнения видно, что движение
m
m 2
колебательное; косинус – функция периодическая с периодом 2 ; период колебания составит T 
3
2
t    t 
3
2
2

. Наибольшее смещение xmax достигается, когда
. В этот момент времени x  xmax 
A
m 2
dx
 0 , т. е.
dt
. Скорость v достигает мак-
dv


 0 , т. е. t  . Значит, в момент времени t 
dt
2
2
A
скорость достигает значения vmax 
.
m
симального значения, когда
1.5. Движение жидкостей и газов
1.5.1. Линии и трубки тока. Уравнение неразрывности
несжимаемой струи
Один из разделов механики называется механикой сплошной среды. Он
включает в себя гидродинамику, газовую динамику, теорию упругости. В этих
дисциплинах вещество рассматривается как непрерывная среда. Познакомимся с
основами гидродинамики. Гидрадинамика изучает движение несжимаемых жидкостей и взаимодействие таких жидкостей с твердыми телами.
Состояние движения жидкости можно определить, задав в каждой точке
пространства вектор скорости как функцию времени. Такая совокупность векторов v образует поле вектора скорости. Его можно изобразить следующим образом. В движущейся жидкости проведем линии так, чтобы касательная к ним в
каждой точке совпадала по направлению с вектором скорости (рис. 1.5.1). Эти линии называются линиями тока.
Рис. 1.5.1
65
Линии тока проводят так, чтобы их густота (отношение числа линий, пронизывающих перпендикулярную к ним площадку, к величине этой площадки
N
)
S
была пропорциональна величине скорости в данном месте. Тогда по картине линий тока можно судить о величине скорости в разных точках пространства: где
линии гуще, там скорость выше.
Поскольку вектор скорости в каждой точке пространства может меняться со
временем, то и линии тока могут меняться. Если v в каждой точке пространства
постоянен во времени, то течение называется стационарным. При этом картина
линий тока неизменна.
Часть жидкости, ограниченная линиями тока, называется трубкой тока.
Поскольку вектор v касается линии тока, то он касается и поверхности трубки
тока, а значит, частицы при своем движении не пересекают стенок трубки тока.
Рассмотрим трубку тока настолько тонкую, что можно считать в каждом сечении скорость постоянной величиной по всему сечению (рис. 1.5.2). Если жидкость несжимаема (   const ), то количество жидкости между сечениями S1 и S 2
должно быть постоянно, то есть сколько жидкости войдет через сечение S1 ,
столько же должно выйти через сечение S 2 . Трубка тока узкая, и t мало . За это
время через сечение S1 войдет объем жидкости, равный v1S1t , так как через S1
пройдут частицы жидкости, которые находились от него на расстоянии, не больS1v1t
 S1v1 .
t
Такой же объем жидкости должен выйти через сечение S 2 . Но через сечение S 2
шем v1t . За единицу времени объем вошедшей жидкости будет равен
пройдет в единицу времени объем жидкости, равный S 2 v2 . Значит, S1v1  S2v2 . Сечения S1 и S 2 выбраны произвольно, значит, полученное равенство справедливо
для любой пары сечений.
Рис. 1.5.2
Для несжимаемой жидкости произведение Sv в любом сечении одной и той
же трубки тока должно быть одинаковым: Sv  const . Это равенство называется
уравнением неразрывности струи несжимаемой жидкости.
Из уравнения видно, что в трубке уменьшающегося сечения жидкость будет
двигаться с ускорением.
Еще раз подчеркнем, что уравнение неразрывности справедливо только для несжимаемой жидкости. Несжимаемыми можно считать капельные жидкости и газы
при их движении со скоростями до 100 м с .
Пример 1. Найти скорость течения по трубе углекислого газа, если известно, что за t  0,5 ч через поперечное сечение трубы протекает m  0,51 кг газа.
66
Плотность газа принять равной   7,5 кг м3 . Диаметр трубы равен d  2 см . Жидкость идеальная.
Решение. Объем газа, протекающего через поперечное сечение трубы за t  1 с
равен V 
m
. С другой стороны, этот объем равен произведению скорости жидкости и
t
d2
площади поперечного сечения: V  vS  v
получим: v  4m

2
 d t
4
. Приравнивая два выражения для объема,
4  0,51
 0,12 м с .
3.14  0.022  7,5 1800
1.5.2. Уравнение Бернулли
Жидкость (или газ), вязкостью которой можно пренебречь, называется идеальной.
Выделим в идеальной стационарно текущей жидкости трубку тока очень
малого сечения (рис. 1.5.3). За время t объем жидкости между сечениями S1 и S 2
переместится вдоль трубки тока: сечение S1 перейдет в сечение S1 ; сечение S 2 перейдет в сечение S 2 . Первое сечение пройдет путь l1 , второе – l2 .
Рис. 1.5.3
В силу неразрывности струи объем жидкости, вошедшей в объем между сечениями S1 и S 2 , равен вышедшему объему жидкости. Значит, заштрихованные на
рисунке объемы будут иметь одинаковую величину: V1  V2  V . Энергия каждой частицы жидкости складывается из потенциальной энергии в поле сил земного тяготения и кинетической энергии. Так как течение стационарно, любая частица жидкости, проходя через выбранную точку (например, точку О), имеет такую
же скорость, как и частица, находившаяся в этой точке в начальный момент времени. Значит, и кинетическая энергия всех частиц в выбранной точке будет одинаковой. Отсюда следует, что приращение энергии Е всего рассматриваемого
объема можно определить как разность энергий заштрихованных объемов V2 и
V1 . Пусть сечение трубки и путь L настолько малы, что во всех точках заштрихованного объема ( V2 или V1 ) значения скорости v , давления P и высоты h
одинаковы. Тогда приращение энергии можно записать следующим образом:
 Vv22
  Vv12

E  
 Vgh2   
 Vgh1  ,
 2
  2

67
где  – плотность жидкости.
Поскольку жидкость идеальная, то трение отсутствует. Поэтому приращение энергии обеспечивается работой сил давления над выделенным объемом. Силы давления на боковую поверхность перпендикулярны в каждой точке перемещениям частиц жидкости, к которым они приложены, и, вследствие этого, работы
не совершают. Отлична от нуля только работа сил, приложенных к сечениям S1 и
S 2 . Она равна
A  PS
1 1L1  P2 S2 L2   P1  P2  V .
Приравняв значения работы и энергии, сократив на V и сгруппировав члены, получим:
 v12
2
  gh1  P1 
 v22
2
  gh2  P2 .
Сечения S1 и S 2 взяты призвольно, поэтому можно утверждать, что в любом
2
сечении трубки тока выражение  v   gh  P имеет одинаковое значение.
2
Так как при выводе этого уравнения было сделано предположение о малости площади сечения трубки тока, то это уравнение будет абсолютно точным при
стремлении площади сечения трубки к нулю, т. е. при превращении трубки тока в
линию тока.
Таким образом, в стационарно текущей идеальной жидкости вдоль любой линии
тока выполняется условие:
v2
2
  gh  P  const . Это уравнение носит имя Бернулли.
Оно довольно хорошо выполняется и для реальных жидкостей с малой вязкостью.
Если разность высот рассматриваемых точек линии тока невелика и ею
можно пренебречь, полагая h1  h2 , то уравнение Бернулли упрощается:
 v12
2
 P1 
 v22
2
 P2 .
Из этого уравнения видно, что с увеличением скорости снижается давление.
На этом принципе работает водоструйный вакуумный насос (рис. 1.5.4).
Рис. 1.5.4
Скорость воды в сужающемся месте увеличивается, давление снижается,
становясь ниже атмосферного; происходит подсос воздуха из окружающего пространства.
Уравнение Бернулли позволяет легко рассчитать истечение жидкости из небольшого отверстия в широком открытом сосуде.
68
Пример 2. На дне цилиндрического сосуда имеется круглое отверстие диаметром d  1 см . Диаметр сосуда D  0,5 м . Найти зависимость скорости v понижения уровня воды в сосуде от высоты h этого уровня. Найти численное значение
этой скорости для высоты h  0, 2 м .
Решение. Обозначим через S1 площадь поперечного сечения сосуда и v1 – скорость течения воды в нем (скорость понижения уровня воды в сосуде), S 2 – площадь
поперечного сечения отверстия и v2 – скорость вытекания воды из отверстия. По теореме Бернулли,   v12  2   gh    v22  2 или v12  2 gh  v22 . В силу неразрывности струи
S1v1  S2v2 , или v2   v1S1  S2 . Подставляя последнее равенство в уравнение Бернулли и
решая его относительно v1 , получим: v1  S2


2gh
S  S22
2
1
. Так как S1   D 2  4 и
2gh
2
. Так как D 4  d 4 , то приближенно v1   d D  2 gh .
4
4
D d
Отметим, что если d  D , то v1  2gh . При h  0, 2 м имеем v1  8 104 м с .
S2   d 2
4 , то v1  d 2
Полученное выражение для скорости истечения жидкости через отверстие
носит название формулы Торричелли.
1.5.3. Вязкое трение
В реальных жидкостях всегда проявляется вязкость (трение, приводящее к
прекращению движения жидкости).
Рассмотрим следующий опыт. Две параллельные пластинки погружены в
жидкость. Размеры пластин много больше расстояния d между ними (рис. 1.5.5).
Рис. 1.5.5
Нижняя пластина закреплена, верхняя приводится в движение с постоянной
скоростью v0 под действием определенной и постоянной силы F . Опыт показывает,
что ускорение движущейся пластины равно нулю. Значит, сила F уравновешивается
равной ей противоположно направленной силой. Это и есть сила трения Fтр , действующая на пластину при ее движении в жидкости. Ньютон, исследуя этот факт,
установил, что сила трения пропорциональна скорости движения пластины и ее
площади и обратно пропорциональна расстоянию между пластинами:
Fmp  
69
v0
S.
d
(*)
Здесь  – коэффициент внутреннего трения (коэффициент вязкости). Нижняя пластина подвергается действию силы Fmp , равной Fтр . Эта сила уравновешивается силой F  со стороны пружины.
Значит, при движении двух параллельных пластин, погруженных в жидкость,
между ними возникает взаимодействие с силой Fтр . Воздействие верхней пластины на
нижнюю осуществляется через жидкость, передаваясь от одного слоя к другому. Если
мысленно провести между пластинами плоскость, параллельную пластинам, то можно
утверждать, что верхняя часть жидкости действует на нижнюю с силой Fmp , а нижняя
на верхнюю – с силой Fтр , причем обе силы определяются одним и тем же выражением
(*). Это выражение определяет не только силу, действующую между пластинами, но
силу трения между соприкасающимися слоями жидкости.
Если измерить скорость жидкости в разных слоях, то обнаружится, что она
изменяется в направлении, перпендикулярном нижней пластине по линейному закону: v  z  
v0
z.
d
Вследствие вязкости частицы жидкости, соприкасающиеся с пла-
стинами, как бы прилипают к ним и имеют ту же скорость, что и пластины. Дифференцируя выражение для скорости, имеем:
всегда положительна, то и производная
dv  z  v0
 . Поскольку правая часть
dz
d
dv  z 
должна быть положительна. Но ее
dz
знак зависит от направления оси z . Поэтому для того, чтобы формула была справедливой, при дифференцировании взят модуль производной. Подставив это равенство в закон Ньютона (*), получим:
Fmp  
dv
S.
dz
Эта зависимость определяет модуль силы трения. Градиент dv dz показывает, как быстро изменяется скорость в направлении оси z .
Тела шарообразной формы при движении в вязкой жидкости испытывают сопротивление трения, определяемое эмпирическим законом, установленным Стоксом:
Fтр  6 rv .
Здесь r – радиус шара. Закон справедлив при малых значениях скорости v .
Вязкость жидкости характеризуется коэффициентом вязкости. Единицей
вязкости в СИ служит такая вязкость, при которой градиент скорости с модулем
1
м с
м
приводит к возникновению силы трения в 1Н на поверхности в 1м 2 . Эта еди-
ница называется паскаль-секунда – [ Па  с] . Коэффициент вязкости зависит от температуры, причем характер этой зависимости для жидкостей и газов различен.
Для жидкостей коэффициент вязкости с ростом температуры уменьшается, для
газов – наоборот. Это объясняется различием механизмов внутреннего трения у
жидкостей и газов.
Пример 3. Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Во сколько раз сила
трения, действующая на всплывающий шарик, больше веса этого шарика?
70
4
3
Решение. На всплывающий шарик действуют: сила Архимеда FA   r 3  ж g ( r –
4
3
радиус шарика), сила веса P  mg   r 3 ш g и сила сопротивления Стокса Fc . Поскольку шарик поднимается с постоянной скоростью, то равнодействующая всех сил равна
нулю: FA  P  Fc  0 . Все силы направлены по вертикали: FA – вверх, P и Fc – вниз.
Проектируя векторное уравнение на вертикальное направление, получаем:
FA  P  Fc  0 или Fc  FA  P . Учитывая, что  ж  4 ш , имеем: Fc  4 r 3 ш g . Отсюда
Fc P  3 .
1.5.4. Ламинарное и турбулентное течения
При наблюдении издалека дыма, выходящего из трубы, мы видим сплошную струю, равномерно вытекающую из отверстия трубы. При приближении к
трубе мы увидим беспорядочные клубы дыма, перемешивающиеся между собой.
Значит, кроме общего движения по ветру клубы дыма совершают различные движения то в одну, то в другую сторону. Это явление – наличие в потоке беспорядочных движений частиц среды – называется турбулентностью. Благодаря турбулентности происходит перемешивание потока. В дымовой струе беспорядочные
движения воздуха переносят частицы дыма во все стороны: струя расширяется и
на большом расстоянии от трубы оказывается размытой во все стороны. Этот результат турбулентности виден и на большом расстоянии.
Турбулентность – очень распространенное явление. Турбулентны течение
воды в реке и движение воды в водопроводных трубах. При движении тела в воздухе за ним всегда образуется турбулентный след и т. д. (Турбулентность в потоках жидкости или газа отсутствует только при определенных условиях.) Наблюдать турбулентное движение легко, если ввести в поток жидкости подкрашенную
струйку – она уже на небольшом расстоянии от места введения равномерно распределяется по всему сечению потока. Турбулентное течение нестационарно.
Если уменьшать скорость потока жидкости или газа, то можно заметить,
что, начиная с некоторой скорости потока, окрашенная струйка, введенная в поток, перестанет расплываться и вытянется вдоль потока. При малой скорости потока турбулентность исчезает, и течение становится струйным. Такое движение
жидкости или газа называется ламинарным. Оно стационарно.
Если опять увеличить скорость потока, течение снова станет турбулентным.
Опыт показывает, что в узких трубах турбулентность прекращается и появляется
при больших скоростях раньше, чем в широких трубах. В капиллярах движение
жидкости всегда ламинарно. Течение вязких жидкостей (глицерин, масло) может
оставаться ламинарным при значительно больших скоростях, чем течение текучих жидкостей (вода, спирт). При нормальном кровообращении кровь протекает в
артериях без турбулентности. Значит, течение крови по кровеносным сосудам
описывается законами ламинарного течения.
71
Английский ученый Осборн Рейнольдс установил, что характер течения жидкости или газа зависит от значения безразмерной величины Re 
 vl
, впоследствии

названной числом Рейнольдса. Здесь  – плотность среды, v – средняя по сечению
скорость,  – вязкость, l – характерный размер поперечного сечения потока.
При малых числах Рейнольдса наблюдается ламинарное течение. Начиная с
некоторого значения Re , называемого критическим, течение приобретает турбулентный характер. Для течения в круглой трубе Re кр  2000 , если за характерный
размер принят диаметр трубы.
В число Рейнольдса входят две величины, зависящие от свойств жидкости:
плотность  и вязкость  . Их отношение     называется кинематической вязкостью, величина  называется динамической вязкостью. Используя выражение
для  , число Рейнольдса можно записать следующим образом: Re  vl  .
Пример 4. Считая, что ламинарность движения жидкости (или газа) в цилиндрической трубе сохраняется при Re  2000 (если при вычислении Re в качестве характерного размера взять диаметр трубы), показать, что условия примера
соответствуют ламинарному движению. Кинематическую вязкость принять равной   1,33 106 м2 с .
Решение. При скорости течения газа v  0,12 м с в трубе диаметром
d  2 см  0, 02 м число Рейнольдса будет равно Re 
vd


0,12  0, 02
 1800  2000 . Зна1,33 106
чит, течение ламинарно.
1.5.5. Течение Пуазейля
Как уже сказано, течение в трубах малого диаметра (например, движение
крови по кровеносным сосудам) или течение с малыми скоростями будет ламинарным. Найдем закон изменения скорости с расстоянием r от оси трубы.
При движении жидкости в круглой трубе скорость равна нулю у стенок
трубы и максимальна на оси трубы. Выделим воображаемый цилиндрический
объем жидкости радиусом r и длиной l (рис. 1.5.6).
Рис. 1.5.6
В силу стационарности ламинарного течения скорости всех частиц жидкости в трубе постоянного сечения остаются неизменными, т. е. выделенный объем
жидкости движется без ускорения. В соответствии со вторым законом Ньютона
72
сумма всех внешних сил, приложенных к любому объему жидкости, равна нулю.
На основания выделенного цилиндрического объема действуют силы давления,
сумма которых равна ( P1  P2 ) r 2 . Эта сила действует в направлении движения
жидкости. На боковую поверхность цилиндра действует сила трения
Fтр  
dv
dv
2 rl . Здесь
– значение градиента скорости на расстоянии
dr
dr
r от оси
трубы.
Уравнение стационарности имеет вид:
dv
2 rl .
(**)
dr
dv
dv
  . Из равенства (**) имеем:
Скорость убывает от оси трубы, поэтому
dr
dr
 P1  P2   r 2  

dv  P1  P2  r

.
dr
2 l
Это дифференциальное уравнение первого порядка с разделяющимися переменными. Разделяем переменные:
P1  P2
rdr .
2 l
dv  
Интегрируем:
v r   
P1  P2 2
r C .
4l
Постоянную интегрирования C определим из условия v  0 при r  R (на
стенке трубы). Полагая r  R , имеем: 
P1  P2 2
P P
R  C  0 . Отсюда C  1 2 R 2 .
4l
4l
P1  P2 2  r 2 
Следовательно, v  r  
R 1  2  .
4l
 R 
P P
На оси трубы v0  v  0   1 2 R 2 .
4l
 r2 
Значит, общая формула будет иметь вид: v  r   v0 1  2  .
 R 
При ламинарном течении скорость изменяется с расстоянием от оси трубы по
параболическому закону (рис. 1.5.7).
Рис. 1.5.7
Полагая течение ламинарным, вычислим поток жидкости Q , т. е. объем жидкости, протекающий через поперечное сечение трубы радиусом R за единицу вре73
мени. Разобьем сечение на кольца ширины dr (рис. 1.5.8). Через кольцо радиусом r
за секунду пройдет объем жидкости, равный произведению площади кольца 2 rdr на
скорость течения в точках, отстающих от оси трубы на расстоянии r .
Рис. 1.5.8
Приняв во внимание общую формулу распределения скорости по радиусу

2


R 
трубы, получим: dQ  v  r   2 rdr  v0 1  r 2  2 rdr . Для получения полного потока Q
это выражение нужно проинтегрировать по радиусу r от 0 до R :
 r2 
1
1
Q   v0 1  2  2 rdr   R 2v0  Sv0 , .
2
2
 R 
0
R
где S – площадь сечения трубы.
Отсюда следует, что при ламинарном течении среднее по сечению значение
скорости равно половине максимального значения, которое достигается на оси
трубы. Если заменить v 0 его выражением, то получим:
Q
( P1  P2 )  R 4
.
8l
Это – формула Пуазейля. Поток жидкости (расход) пропорционален перепаду давления на единицу длины трубы, четвертой степени радиуса трубы и обратно пропорционален вязкости жидкости. Все это справедливо только для ламинарного течения. Формулу Пуазейля используют для определения вязкости жидкости. Пропуская жидкость через капилляр известного радиуса, измеряют перепад
давления
P1  P2
и расход Q ; по формуле Пуазейля вычисляют  .
l
Пример 5. В боковую поверхность цилиндрического сосуда с радиусом
R  2 см вставлен горизонтальный капилляр с внутренним радиусом r  1 мм и
длиной l  2 см . В сосуд налито касторовое масло, динамическая вязкость которого равна   12
г
. Найти зависимость скорости
см  с
v понижения уровня касторово-
го масла в цилиндрическом сосуде от высоты h этого уровня над капилляром.
Найти численное значение этой скорости при h  26 см .
Решение. Скорость понижения уровня касторового масла в сосуде зависит
от скорости протекания масла через капилляр. Объем масла, протекающего через
капилляр за время t , определяется формулой Пуазейля: Q 
 r 4t p
. В нашем слу8l
чае разность давлений на концах капилляра обусловлена гидростатическим дав74
лением слоя жидкости, т. е. p   gh . С другой стороны, Q  S1v1t , где v1 – скорость
r 2  gh
. Но уравнение нераз8l
рывности дает: v1S1  vS , где v – скорость понижения уровня масла в сосуде и S –
протекания масла через капилляр. Отсюда имеем: v1 
площадь поперечного сечения сосуда. Тогда окончательно
r 4  gh
v
. При
8l R 2
h  0, 26 м скорость понижения уровня масла в сосуде составит v  3 105 м с .
1.6. Основы механики упругих тел
В п. 1.3 указывалось, что соприкасающиеся тела действуют друг на друга с
некоторой силой лишь в том случае, если они деформированы, например, сжаты.
Деформация нас интересовала лишь постольку, поскольку с ней связано появление тех или иных сил. Нас не интересовали изменения объема и формы тел при
деформациях. Однако при точных расчетах деформации необходимо принимать
во внимание.
1.6.1. Упругие и пластические деформации
В природе абсолютно твердых тел не существует. Все реальные тела под
действием сил изменяют свою форму и размеры, т. е. деформируются. Однако
слегка деформированная стальная пластинка после устранения сил восстановит
свою форму, а свинцовая пластинка такого же размера – нет.
Деформации, которые полностью исчезают при устранении деформирующих сил, называются упругими. Деформации, которые не исчезают по снятию
деформирующих сил, называются пластическими.
Строго говоря, не существует ни полностью упругих, ни полностью пластических деформаций. Упругая деформация у всех тел с увеличением времени действия сил переходит в пластическую. При коротком времени воздействия сил тела, подверженные пластической деформации, могут повести себя как упругие.
Переход упругой деформации в пластическую зависит и от величины самой
деформации. Чем больше деформация, тем меньший промежуток времени требуется для ее перехода в пластическую.
Существует несколько видов деформации – растяжение, сжатие, изгиб, кручение, но, как доказывается в теории упругости, все они могут быть сведены к
одновременно происходящим деформациям растяжения или сжатия и сдвига.
Примером одностороннего или продольного растяжения может служить
проволока, на которой подвешен груз (рис. 1.6.1 а).
75
Рис. 1.6.1
При таком растяжении тела удлиняются и одновременно несколько уменьшаются в поперечных размерах. Примерами одностороннего или продольного сжатия
являются колонны, поддерживающие часть здания (рис. 1.6.1 б). При одностороннем
сжатии тело немного расширяется в поперечном направлении.
В случае сдвига деформации обусловлены двумя равными противоположно
направленными моментами сил. Представим себе брус, имеющий форму прямоугольного параллелепипеда и стоящий на горизонтальной поверхности (рис. 1.6.2 а).
Рис. 1.6.2
Сила тяжести Р бруса полностью уравновешивается реакцией N опоры.
Пусть к брусу приложена горизонтальная сила F такая, что брус перекашивается,
но еще не скользит по полу (рис. 1.6.2 б). Поскольку брус покоится, значит, на него
действует еще одна сила, равная по величине силе F и направленная в противоположную сторону. Конечно, этой силой является сила трения Fтр , образующая вместе с силой F пару сил, которая должна была бы вызвать ускоренное вращение
бруса вокруг оси. Но брус покоится; следовательно, существует другая пара сил,
уравновешивающая первую. Указать ее нетрудно. Если при отсутствии силы F реакция опоры приложена к брусу в точке А , то при наличии силы F точка приложения реакции опоры к телу сместится в другую точку, скажем, в точку В , удаленную от точки А на расстояние, большее, чем смещение центра масс, к которому
приложена сила тяжести. В результате получается новая пара сил Р и N , которая
действует в направлении, противоположном паре F и Fтр . Так как брус покоится,
эти пары уравновешивают друг друга. Наличие этих пар сил связано с деформацией, которая приводит к перекашиванию бруса. Деформация, при которой прямой
параллелепипед, взятый в теле, превращается в наклонный, имеющий объем равный объему недеформированного параллелепипеда, называется сдвигом.
76
Если деформация сдвига из упругой переходит в пластическую, то возникает смещение одних слоев тела вдоль других. Пластическая деформация сдвига отчасти сходна с течением жидкости: при течении жидкости ее слои непрерывно
сдвигаются один вдоль другого. Упругость сдвига может служить признаком для
отличия твердого состояния от жидкого: при жидком состоянии вещества упругий
сдвиг невозможен.
1.6.2. Закон Гука
Возьмем пружину, имеющую в недеформированном состоянии длину l0 , и
приложим к ее концам равные по величине, противоположно направленные силы
F1 и F2 (рис. 1.6.3).
Рис. 1.6.3
Под действием этих сил пружина растянется на некоторую величину l , после
чего наступит равновесие. В состоянии равновесия внешние силы F1 и F2 будут уравновешены упругими силами, возникшими в пружине в результате деформации. Опыт
показывает, что при небольших деформациях удлинение пружины l оказывается
пропорциональным растягивающей силе: l  F ( F  F1  F2 ). Соответственно упругая сила оказывается пропорциональной удлинению пружины: F  k l .
Утверждение о пропорциональности между упругой силой и деформацией
носит название закона Гука. Коэффициент пропорциональности k называется коэффициентом упругости пружины.
Упругие напряжения возникают по всей пружине. Любая часть пружины
действует на другую часть с силой, определяемой законом Гука. Если разрезать
пружину пополам, та же по величине упругая сила будет возникать в каждой из
половин при в два раза меньшем удлинении. Отсюда можно заключить, при заданных материале пружины и размерах витка величина упругой силы определяется не абсолютным удлинением пружины l , а относительным удлинением l l0 .
При сжатии пружины также возникают упругие напряжения, но другого
знака. Закрепим один конец пружины так, чтобы он был неподвижным
(рис. 1.6.4), а удлинение пружины будем рассматривать как координату x другого
ее конца, отсчитываемую от его положения, отвечающего недеформированной
пружине. Кроме того, обозначим проекцию силы Fупр на ось x через Fx . Можно
написать, что Fx  kx . Проекция упругой силы на ось x и координата x всегда
имеют разные знаки.
77
Рис. 1.6.4
Рассмотрим теперь однородный стержень длиной l и площадью поперечного сечения S (рис. 1.6.5), к концам которого приложены направленные вдоль его
оси силы F1 и F2 ( F1  F2  F ), в результате чего длина стержня меняется на величину l . При растяжении l  0 , при сжатии l  0 .
Сила, действующая на единицу площади поперечного сечения, называется
напряжением:   F S . Если сила направлена по нормали к поверхности, напряжение
называется нормальным, если же по касательной к поверхности – тангенциальным.
Рис. 1.6.5
Как и в случае с пружиной, мерой, характеризующей степень деформации,
испытываемой телом, является его относительная деформация. Так, относительное изменение длины стержня, т. е. его продольная относительная деформация,
равна   l l , относительное изменение поперечного размера (сжатие) равна
   d d , где d – диаметр стержня.
Относительные деформации  и   всегда имеют разные знаки: при растяжении
  0 ,    0 ; при сжатии   0 ,    0 . Между этими деформациями существует связь,
установленная опытным путем:      . Здесь  – положительный коэффициент, зависящий от свойств материала и называемый коэффициентом Пуассона.
Закон Гука справедлив и для стержней при малых их деформациях: F  k l ( k –
коэффициент
упругости).
Учитывая,
что
можно
написать:
F S ,
 S  k l   S l  k   
kl
 . Нормальное напряжение оказывается пропорциональS
78
ным относительной деформации. Коэффициент пропорциональности называется модулем Юнга: E  kl S .
Пример 1. Вычислить абсолютное и относительное изменения объема
стального стержня, имеющего длину l  10 м и поперечное сечение S  25 см 2 , если к нему приложено растягивающее усилие F  35 104 H . Коэффициент Пуассона
  0,3 .
Решение. Длина образца после деформации равна l1  l  l  l 1 

l 
  l 1    .
l 
Площадь после деформации равна S1  S 1      S 1    , где  и   – относительные деформации растяжения и сжатия соответственно. Объем после дефор2
2
мации: V1  S1l1  Sl 1    1     V 1    1    , где V – первоначальный объем.
Так как  до предела пропорциональности есть малая величина, то ее квадратом
можно пренебречь. Тогда
2
V1  V 1   1  2   ; V  V1  V  V  1  2  
V  7 106 м3 ;
2
lF
1  2  ; V  F 1  2  ;
E
V
ES
V
 0, 028% .
V
1.6.3. Диаграмма деформирования
Деформация подчиняется закону Гука до известного предела. Связь между деформацией и напряжением обычно представляют в виде диаграммы напряжений.
Примерное поведение зависимости напряжения от деформации видно из рис. 1.6.6.
Рис. 1.6.6
Видно, что линейная зависимость, установленная Гуком, выполняется лишь в
очень узких пределах до так называемого предела пропорциональности (  п ). При
дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость
 ( ) уже не линейна), и до предела упругости (  у ) остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации, и график,
описывающий возвращение тела в первоначальное состояние после прекращения
действия силы, изобразится не кривой ВО , а параллельной ей – CF . Напряжение, при
котором появляется заметная остаточная деформация (  0, 2% ), называется пределом
текучести (  Т ) – точка С на кривой. В области СD деформация возрастает без уве79
личения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область
текучести значительна, называются вязкими, материалы, для которых же она, практически, отсутствует – хрупкими. При дальнейшем растяжении (за точку D ) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения,
называется пределом прочности (  р ).
Диаграмма напряжений для реальных твердых тел зависит от различных
факторов. Одно и то же твердое тело может при кратковременном действии сил
проявлять себя как хрупкое, а при длительных, но слабых силах является текучим.
1.6.4. Потенциальная энергия деформации
Вычислим потенциальную энергию упругорастянутого (сжатого) стержня,
которая равна работе, совершаемой внешними силами при деформации:
l
П  А   Fdx ,
0
где x – абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до l . Согласно закону Гука F  kx  ESx l . Поэтому
П
l

0
ES
1 ES
2
xdx 
 l  ,
l
2 l
т. е. потенциальная энергия упругорастянутого стержня пропорциональна
2
квадрату деформации  l  .
Пример 2. К проволоке, закрепленной верхним концом, подвешивается груз
массой т , под действием которого проволока удлиняется на величину l . Показать, что изменение потенциальной энергии в два раза меньше изменения потенциальной энергии груза. Как это согласуется с законом сохранения энергии?
Решение. Уменьшение потенциальной энергии груза E1  mg l . Увеличение
потенциальной
E2  mg
энергии
E2
проволоки
l E1
.

2
2
 l 
k
2
2
.
Но
k l  mg .
Отсюда
1.6.5. Деформация сдвига
В заключение рассмотрим кратко деформацию сдвига. Возьмем однородное
тело, имеющее форму прямоугольного параллелепипеда, и приложим к его противолежащим граням силы F1 и F2 ( F1  F2  F ), направленные параллельно этим
граням (рис. 1.6.7).
80
Рис. 1.6.7
Если действие сил будет равномерно распределено по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникнет
тангенциальное напряжение   F S ( S – площадь грани). Под действием напряжений тело деформируется так, что одна грань сместится относительно другой на
некоторое расстояние а . Если тело мысленно разбить на элементарные параллельные рассматриваемым граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев.
При деформации сдвига любая прямая, первоначально перпендикулярная
слоям, повернется на некоторый угол  . В качестве характеристики деформации
сдвига берется величина   a b  tg , называемая относительным сдвигом (смысл
величин a и b ясен из рис. 1.6.7). При упругих деформациях угол  бывает очень
мал. Поэтому можно tg   . Следовательно, относительный сдвиг  оказывается
равным углу сдвига  .
Опыт показывает, что относительный сдвиг пропорционален тангенциальному
напряжению:

1

G
.
Это выражение носит название закона Гука при сдвиге. Коэффициент G зависит только от свойств материала и называется модулем сдвига. Он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45 ( tg  1 ),
если бы при столь больших деформациях не был превзойден предел упругости. Измеряется G , как и модуль Юнга E , в паскалях.
Пример 3. Определить толщину нити, на которой подвешена рамка зеркального гальванометра, если под действием вращающего момента М  0,3пН  м она поворачивается на угол   2 . Длина нити l  10 см . Модуль сдвига материала нити
G  6,5 ГПа .
Решение. Выведем выражение для вращающего момента при кручении нити
(цилиндра радиусом R и длиной l ). Как видно из рис. 1.6.8, при повороте верхнего
основания стержня относительно нижнего на угол  различные слои стержня смещаются на разную величину: крайний цилиндрический слой на S  R , а слой радиусом r сместится на s  r . Поэтому угол сдвига каждого цилиндрического слоя
r 
r

зависит от r , а по закону Гука  r  Gr  G r , упругие касательные напряжеl
l
ния в слоях тоже прямо пропорциональны расстоянию слоя от оси. Отсюда для эле81
ментарного момента касательного напряжения, действующего на поверхности цилиндрического слоя радиусом
r
и толщиной dr , имеем: dM r   r Sr r 
G
r  2 rdr  r .
l
Про-
интегрировав последнее выражение по радиусу, получим выражение для вращающего
момента: M вр 
D 2

0
2 G 3
 GD 4
r dr 
.
l
32l
Рис. 1.6.8
Используя условия задачи, получаем: D  4
82
32M врl
 G
 3  мкм  .
2. Молекулярная физика
2.1. Молекулярно-кинетическая теория газов
2.1.1. Основные понятия
Молекулярная физика – раздел физики, изучающий строение и свойства
вещества, исходя из молекулярно-кинетических представлений. Любое тело –
твердое, жидкое, газообразное – состоит из огромного числа обособленных частиц – молекул, которые постоянно находятся в беспорядочном хаотическом
движении. Доказательством существования хаотического движения служит известное из школьного курса физики броуновское движение. Это явление заключается в том, что очень малые частицы, взвешенные в жидкости, находятся в состоянии беспорядочного движения, которое не зависит от внешних причин. Броуновские частицы совершают движение под беспорядочными ударами молекул.
Цель молекулярно-кинетической теории (м-к. т.) – объяснить те свойства
тел, которые мы наблюдаем на опыте (давление, температуру и т. п.), как суммарный результат действия молекул. М-к. т. не рассматривает отдельные молекулы, а
пользуется статистическими методами, усредняя величины, которые характеризуют движение большой совокупности частиц. Отсюда второе название – статистическая физика.
Изучением различных свойств тел и изменений состояния вещества наряду
с м-к. т. занимается и термодинамика. Но в отличие от м-к. т. термодинамика изучает макроскопические свойства тел, не интересуясь микроскопической картиной.
Термодинамика рассматривает протекание процессов, не вводя в рассмотрение
молекулы и атомы.
В основе термодинамики лежат несколько фундаментальных законов (называемых началами). Это опытные законы, установленные на основании огромного количества опытных данных. Поэтому и выводы термодинамики имеют общий характер.
Подходя к рассмотрению изменений состояния вещества с различных точек
зрения, м-к. т. и термодинамика взаимно дополняют друг друга. По существу, это
одно целое.
Введем некоторые параметры, которыми пользуется м-к. т.
Относительной атомной массой химического элемента (или просто атомной массой) называется отношение массы атома данного элемента к
1
12
массы
атома изотопа углерода 12С (12 – массовое число, равное сумме числа протонов и
числа нейтронов в ядре). Обозначается Аr .
Относительной молекулярной массой вещества (или просто молекулярной
массой) называется отношение массы молекулы данного вещества к
атома изотопа углерода 12С . Обозначается М r .
83
1
12
массы
Единица массы, равная
1
массы атома изотопа углерода
12
C,
12
называется
атомной единицей массы mед (измеряется в кг).
Используя эти обозначения, можно написать:
 масса атома элемента = Аr mед ;
 масса молекулы вещества = M r mед .
Количество вещества, в котором содержится число частиц (атомов, молекул, электронов и т. п.), равное числу атомов в 0,012 кг изотопа углерода 12С ,
называется молем.
Число частиц, содержащихся в одном моле вещества, называется числом
Авогадро, полученным опытным путем: N A  6, 022 1023 моль1 .
Масса 1 моля называется молярной массой М :
M  M r mед N A .
Для углерода 12C :
M  0, 012 кг
 0, 012
моль
; M r mед  12 тед 
кг
 N A моль112  тед кг.
моль
0, 012
 1, 66 1027 кг .
12  6, 022 1023
кг
кг
кг
N A  mед  0, 001
 М  М r  0, 001
 0, 001 М r

моль
моль
моль
г
 М  Мr
.
моль
Отсюда тед 
Масса моля, выраженная в граммах, численно равна молекулярной массе.
Теперь оценим размеры молекул. Предполагая, что молекулы (например, воды)
располагаются близко друг к другу, разделим объем одного моля воды на число молекул в нем. Моль воды, т. е. 18 г ( H 2O : атомная масса водорода равна 1, атомная масса
кислорода – 16) занимает объем 18 см3=18·10–6 м3. На долю одной молекулы приходится объем 18 106   6 1023   30 1030 м3 . Отсюда линейные размеры молекулы
 3 30 1030  3 1010 м  3 А . Размеры других молекул имеют такой же порядок.
Основными параметрами, определяющими состояние газа, являются давление Р , температура Т и объем V .
Температура – одно из основных понятий не только термодинамики, но и
физики в целом. Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В настоящее
время применяются только две температурные шкалы – термодинамическая и
Международная практическая, градуированные, соответственно, в кельвинах ( К )
и в градусах Цельсия (°С).
В Международной практической шкале температура замерзания и кипения
воды при давлении 1,013· 105 Па, соответственно, равна 0 и 100 С . Это так называемые реперные точки.
84
Термодинамическая температурная шкала определяется по одной реперной
точке, в качестве которой взята тройная точка воды (температура, при которой
лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна
273,16 К. Градус Цельсия равен кельвину. В термодинамической шкале температура замерзания воды равна 273.15 К (при давлении 1,013· .105 Па), поэтому, по
определению, термодинамическая температура и температура по Международной
практической шкале связаны соотношением T  273,15  t .
Эти параметры связаны друг с другом и, если эта связь выражена аналитически в виде функции, то эта функция называется уравнением состояния данного
газа, т. е. уравнение состояния должно иметь вид: F  P, T ,V   0 .
Пример 1. Газ массой М  10 кг , молекулы которого состоят из атомов водорода и углерода, содержит n  3,76 1026 молекул. Определить массу атомов углерода и водорода, входящих в молекулу этого газа.
Решение. Масса одной молекулы рассматриваемого газа равна
M
10
m0 

 0, 266 1025 кг . Поскольку атомная единица массы тед  1, 66 1027 кг ,
26
n
3, 76 10
то молекулярная масса этого газа составляет M r 
m0
 16 . В молекулу входят
mед
только атомы водорода и углерода. Атомная масса углерода равна Ar  12 , следовательно, в молекуле газа может быть только один атом углерода и четыре атома
водорода, имеющего атомную массу Ar  1 . Отсюда масса атома углерода, входящего в молекулу, равна mC  mед  Ar  1,99 1026 (кг ) . Для четырех атомов водорода
имеем 4mH  6, 64 1027 кг .
2.1.2. Модель идеального газа
Простейшими свойствами обладает газ, взаимодействие между молекулами
которого пренебрежимо мало. Такой газ называется идеальным. Всякий реальный
газ при достаточном разрежении близок по своим свойствам к идеальному. Некоторые газы (воздух, азот, кислород и др.) и при комнатной температуре и атмосферном давлении мало отличаются от идеального. Особенно близки к идеальному по своим свойствам газы гелий и водород.
Идеальный газ или реальные газы при небольших давлениях с хорошей
точностью подчиняются уравнению:
PV
 const .
T
Выводится оно очень просто. Пусть газ переходит из состояния с параметрами P1 ,V1 , T1 в состояние с параметрами P2 ,V2 , T2 .
Представим себе, что переход произошел в два этапа: сначала изменился
объем газа от V1 до V2 при сохранении постоянства температуры. Получившееся
при этом давление обозначим через Рср . На втором этапе изменилась температура
85
от Т1 до Т 2 при сохранении постоянства объема. При этом давление изменилось
от Рср до Р2 .
На первом этапе переход из первого состояния в промежуточное происходил в соответствии с опытным законом Бойля–Мариотта, согласно которому для
данной массы газа произведение объема газа на его давление при изотермическом
процессе (Т = const) остается постоянным, т. е. PV  const . Значит,
P1 V2

Pср V1
или
PV
1 1
 1.
PсрV2
(*)
На втором этапе переход осуществляется по закону Шарля, согласно которому давление некоторой массы газа при нагревании на 1 С в неизменном объеме
увеличивается на
1
273
часть давления при 0 С , т. е.
1 
273  t
T

P  P0 1 
t   P0
 P0
,
273
273
 273 
где P0 – давление газа при 0 C ; t – температура по шкале Цельсия,  
1
273
–
термический коэффициент давления.
По закону Шарля
Рср  Р0
Отсюда
273  t1
T
273  t2
T
 P0 1 ; P2  P0
 P0 2 .
273
273
273
273
Рср Т1

.
Р2 Т 2
(**)
Умножив выражение (*) на (**) почленно, получим:
PV
T
PV PV
PV
1 1
 1  1 1 2 2
 const .
PV
T2
T1
T2
T
2 2
Это и есть уравнение состояния идеального газа.
2.1.3. Уравнение Клапейрона–Менделеева
В соответствии с законом Авогадро моли всех газов занимают при нормальных условиях ( t  0 C; P  1 атм  1, 013 105 Па ) одинаковый объем, равный
22, 4 103
м3
. Отсюда следует, что для количества газа в 1 моль величина конмоль
станты в уравнении состояния будет одинакова для всех газов, близких по своим
свойствам к идеальному. Обозначается эта константа R , и уравнение состояния
перепишется в виде:
PVm  RT .
Индекс m означает, что речь идет об одном моле газа.
Это уравнение состояния для одного моля газа, близкого по своим свойствам к идеальному. Используя нормальные условия
( T0  273K ; P0  1, 013 105 Па; V0  22, 4 103
м3
), можно вычислить значение газовой
моль
постоянной R :
86
PV
1, 013 105  22, 4 103
 Дж 
0 0
R

 8,31
.
T0
273
 моль  К 
От уравнения для одного моля газа перейдем к уравнению для любой массы
газа m . При нормальных условиях  молей газа занимают объем в  раз больший,
чем 1 моль: V   Vm . Так как  
нение состояния на  , получим:
m
, где M – молярная масса, то, умножая уравM
PVm 
m
m
RT  PV 
RT .
M
M
Это и есть уравнение состояния идеального газа для произвольной массы т .
Оно называется уравнением Клапейрона–Менделеева. Придадим ему другой вид.
Поскольку 1 моль любого вещества, по определению, содержит одинаковое число
молекул N A  6, 022 1023 ( N A – число Авогадро), то отношение
R
 k есть величина
NA
постоянная (эта величина называется постоянной Больцмана. Она имеет более
глубокий физический смысл, чем R ): k 
8,31
дж
 1,38 1023
.
23
6, 022 10
K
Умножив и разделив правую часть уравнения Клапейрона – Менделеева на
N A , получим:
PV   kTN A .
Произведение   N A – это число молекул в массе газа m . Обозначим
  N A  N . Значит, PV  NkT  P 
NkT
N
. Так как  n ( n -концентрация – число моV
V
лекул в единице объема), то P  nkT . Это просто другая запись уравнения Клапейрона – Менделеева.
Пример 2. Удельный объем газа при нормальных физических условиях равен Vуд  5,6 м3 кг . Определить молекулярный вес газа. Что это за газ?
Решение. По уравнению Клапейрона – Менделеева молярная масса газа
равна:
M
RT
8,31 273

 0, 004(кг моль)  4 г моль .
pV уд 1, 013 105  5, 6
Значит, молекулярная масса газа равна M r  4 . Такую молекулярную массу
имеет молекула гелия He2 .
Пример 3. В сварочном цехе стоит 40 баллонов ацетилена (С2 Н 2 ) емкостью
по 40 дм 3 каждый. Все баллоны включены в общую магистраль. После 12 часов
непрерывной работы давление во всех баллонах упало с 1,3 107 Па до 0,7 107 Па .
Определить расход ацетилена за 1 мин, если температура в цехе оставалась неизменной и равнялась 32 С .
Решение. Суммарный объем баллонов V  1600 дм3  1,6 м3 в процессе расходования ацетилена остается постоянным. Молярная масса ацетилена
M  0,026 кг моль . Для начального и конечного состояния газа по уравнению Кла87
пейрона–Менделеева имеем: p1V 
m1
m
RT ; p2V  2 RT
M
M
. Отсюда выражаем началь-
ную и конечную массы газа и находим израсходованную массу газа:
m  m1  m2 
 p1  p2 VM . Разделив израсходованную массу газа на время работы,
RT
найдем расход газа:
q
 p1  p2 VM  1,3  0, 7  107 1, 6  0, 026  0,137 
8,31 305  720
RTt
кг 

.
 мин 
Пример 4. В баллоне емкостью 2м3 содержится смесь азота  N2  и окиси
азота  NO  . Определить массу окиси азота, если масса смеси равна 14 кг , температура 300 К и давление 0,6 106 Па .
Решение. Закон Дальтона гласит: «Давление смеси идеальных газов равно
сумме парциальных давлений входящих в нее газов». Значит, Pсм  PN  PNO . Для
каждой компоненты смеси запишем уравнение Менделеева–Клайперона:
2
PN2V 
m1
m
RT ; PNOV  2 RT . Здесь m1  (14  m2 ) – масса азота в смеси; m2 – масса
M N2
M NO
окиси азота в смеси. Используя таблицу Менделеева, находим молярные массы
компонент смеси:
M N  0,028 кг моль; M NO  0,030 кг моль .
Подставляя в выражение для давления смеси данные задачи, получаем:
2
0, 6 106 
14  т2
т2
8,31 300 
8,31  300  m2  7,83 кг .
0, 028  2
0, 03  2
2.1.4. Основное уравнение молекулярно-кинетической теории
Уравнение Клапейрона–Менделеева связывает давление газа с его температурой. Температура определяет интенсивность хаотического движения молекул, т.
е. кинетическую энергию молекул. Найдем зависимость давления газа от кинетической энергии молекул.
Рассмотрим упрощенную картину хаотического движения молекул. Будем
считать, что молекулы газа движутся вдоль трех взаимно перпендикулярных
направлений (рис. 2.1.1).
Рис. 2.1.1
Если в сосуде N молекул, то в любой момент времени вдоль каждого из
направлений будет двигаться N 3 молекул, причем половина из них (т. е. N 6 )
88
движется вдоль данного направления в одну сторону, половина – в другую. Следовательно, в интересующем нас направлении (например, по нормали к данному
элементу S стенки сосуда) движется 1 6 часть молекул.
Предположим, что все молекулы движутся с одинаковой средней скоростью v .
Тогда за время t до элемента стенки S долетят все молекулы, движущиеся по
направлению к нему и заключенные в объеме V  S  v  t . Число этих молекул равно:
 
1
n
nV  S v t .
6
6
Значит, число молекул, ударившихся об единичную площадку в единицу
времени, будет равно:
1
6
 n v .
Предполагая отражение молекул от стенки зеркальным и считая, что молекулы ударяются о стенку сосуда перпендикулярно, получим, что при ударе каждая молекула передает стенке импульс K  2m v . (Это легко понять, если принять
во внимание, что удар молекулы о стенку сосуда уподобляется удару шара о неподвижную упругую стенку. Скорость молекулы при таком ударе не меняет величины, но изменяет знак (направление) на обратный v   v . Стенка подействовала
на
молекулу
и
изменила
ее
импульс
на
величину K   m v  m v  m v  m v  2m v . По третьему закону Ньютона, молекула
передала стенке импульс K  K   2m v ).
1
6
Единичная площадка испытывает в единицу времени   n v ударов. Стало быть, суммарный импульс, полученный площадкой, будет равен K  2m v
Мы
v 
использовали
среднюю
(среднеарифметическую)
скорость
n v
.
6
молекул
v1  ...  vn
. Более точные вычисления показывают, что должна быть использоn
вана среднеквадратичная скорость vкв 
v12  ...  vn2
.
n
Отсюда
1
K  mn vкв2 .
3
Импульс, полученный площадкой за единицу времени, равен силе, действующей на площадку
dK
F,
dt
а сила, приходящаяся на единицу площади, – дав1
3
ление, оказываемое газом на стенку сосуда. Значит, P  F  K  mn vкв2 . Поскольку m  const , то ее можно внести под знак осреднения:
89
P
n
2 mvкв2
2
mvкв2  n
 n  .
3
3
2
3
Это уравнение называется основным уравнением молекулярно-кинетической
теории. Оно связывает давление газа со средней кинетической энергией поступательного движения молекул.
Вычислим энергию одной молекулы. Умножив обе части основного уравнения м-к. т. на объем одного моля Vm , получим:
PVm 
2
nVm  .
3
Используя уравнение состояния для одного моля PVm  RT и то, что nVm  N A ,
2
3
получаем PVm  N A   RT . Отсюда  
3 RT 3
 kT . Средняя энергия поступа2 NA 2
тельного движения молекул идеального газа не зависит от природы газа и пропорциональна его абсолютной температуре.
Поскольку кинетическая энергия молекулы равна  
ченной зависимости
vкв2 
m vкв2
2
, то из полу-
 от T следует:
3RT 3RT
3RT

 vкв 
( М – молярная масса).
mN A
M
M
2.1.5. Распределение Максвелла
При упрощенном выводе основного уравнения м-к. т. предполагалось, что
скорости всех молекул одинаковы. В действительности же в результате многократных соударений скорость каждой молекулы изменяется по величине и
направлению. Согласно молекулярно-кинетической теории как бы ни изменялись
скорости молекул при столкновениях, средняя квадратичная скорость молекул
при T  const остается постоянной. Это объясняется тем, что в газе, находящемся в
состоянии равновесия, устанавливается некоторое стационарное распределение
молекул по скоростям. Это распределение подчиняется статистическому закону,
теоретически установленному Максвеллом.
Если разбить диапазон скоростей молекул на малые интервалы dv , то на
каждый интервал будет приходиться некоторое число молекул dN  v  , имеющих
скорость, заключенную в этом интервале. Максвелл нашел функцию f  v  , определяющую относительное число молекул dN  v  N , скорости которых лежат в интервале от v до v  dv : f  v   dN  v   Ndv . Пользуясь методами теории вероятности, Максвелл установил вид этой функции:
3
 m  2
f  v   4  0  v 2e
 2 kT 
90
 m0v 2
 2 kT 
.
Из графика этой функции (рис. 2.1.2) видно, что функция достигает максимума
при некотором значении скорости vв , называемом наиболее вероятной скоростью.
Значение этой скорости можно найти, исследовав функцию f  v  на экстремум. Приравняв первую производную по скорости нулю, найдем, что vв  2kT m0  2RT M .
Рис. 2.1.2
Используя функцию распределения молекул по скоростям, можно получить
и выражение для средней арифметической скорости:
Подставив f  v  и проинтегрировав, получим:

1
v   vdN  v    vf  v dv .
N0
0
v  8kT  m0   8RT  M  .
Пример 5. В баллоне емкостью V  0,05 м3 находится   0,12 кмоль газа при
давлении p  0, 6 107 Па . Определить среднюю кинетическую энергию теплового
движения молекулы газа.
Решение. В общем случае средняя энергия молекулы равна    i 2 kT , где
i – число степеней свободы молекулы. (Число степеней свободы – это число независимых переменных, полностью определяющих положение молекулы. Если молекула имеет один атом, ее можно рассматривать как материальную точку, положение которой полностью описывается тремя координатами, т. е. одноатомная
молекула имеет три степени свободы. Двухатомную молекулу можно представить
как систему двух жестко связанных материальных точек. Такая система кроме
возможности перемещаться в направлении трех осей имеет возможность вращаться вокруг осей, проходящих через каждую из точек. Так как материальная точка
не имеет размеров, вращение такой системы вокруг оси, проходящей через обе
точки, лишено смысла. Таким образом, двухатомная молекула может рассматриваться как система с пятью степенями свободы, из которых три поступательные и
две вращательные. Рассуждая аналогично, можно прийти к выводу, что трехатомную молекулу можно рассматривать как систему трех жестко связанных материальных точек, имеющих шесть степеней свободы: три поступательных и три вращательных.)
Тепловое движение молекулы подразумевает поступательное движение, при
3
2
котором   kT . По уравнению Клапейрона–Менделеева имеем: T 
температура газа. Значит,
91
pV
R
, где T –
3 pV 3 1,38 1023  0,6 107  0,05

 0,623 1020 ( Дж) .
2 R
2 120  8,31
  k
2.1.6. Барометрическая формула
При выводе основного уравнения м-к. т. предполагалось, что внешние силы
на молекулы не действуют. Но молекулы любого газа находятся в потенциальном
поле тяготения Земли. Кроме этого, молекулы находятся в непрерывном тепловом
движении. Это приводит к некоторому стационарному состоянию газа, при котором давление газа с увеличением высоты убывает.
Предположим, что поле тяготения однородно, температура постоянна и все
молекулы имеют одинаковую массу. При этом если на высоте h давление равно
p , то на высоте h  dh давление будет равно p  dp . Разность давлений на рассматриваемых высотах будет равна весу газа, заключенного в объеме цилиндра
высотой dh и площадью основания, равной единице:
p   p  dp    gdh ,
где  – плотность газа на высоте h .
В силу малости отрезка высоты dh давление газа в пределах этого отрезка
считаем постоянным и равным p . Тогда
dp    gdh .
Из уравнения состояния идеального газа находим:
  m V  pM RT  .
Подставляя это значение в выражение приращения давления, получаем:
dp
Mg

dh .
p
RT
С изменением высоты от h1 до h2 давление меняется от p1 до p 2 . Интегрируя в этих пределах последнее выражение, получаем:
p2
h
p
dp
Mg 2
Mg
 Mg  h  h   RT 


 p RT  dh  n p12   RT  h2  h1   p2  p1e 2 1 .
p1
h1
Так как высоты отсчитываются от уровня моря ( h1  0 ), последнюю формулу

Mgh
можно переписать так: p  p0e RT . Здесь p0 и p – давления на уровне моря и на
высоте h .
Выражение для p называется барометрической формулой. Барометрическая
формула дает зависимость давления от высоты над поверхностью Земли для воображаемой изотермической атмосферы. Заменим в показателе экспоненты отношение
M R равным ему отношением m k . Кроме этого, заменим давления p0 и p их выражениями в соответствии с уравнением Клапейрона–Менделеева ( p  nkT ). После
несложных преобразований получим:
 p 
 mgh 
n  n0 exp  
  n0 exp    .
 kT 
 kT 
92
Здесь n0 и n – концентрации молекул на уровне моря и на высоте h ; mgh   p –
потенциальная энергия молекулы в поле земного тяготения. Таким образом, распределение молекул по высоте определяется значением их потенциальной энергии. Это
распределение называется распределением Больцмана.
В то время как закон Максвелла дает распределение молекул по значениям
кинетической энергии, закон Больцмана дает распределение молекул по их потенциальным энергиям.
Пример 6. Отношение барометрического давления у поверхности Земли к
давлению на некоторой высоте равно 1,8 . Какую высоту покажет в этой точке
прибор со шкалой, проградуированной по барометрической формуле при t  5 C ,
если у Земли стрелку прибора установить на нуль. Вычислить относительную погрешность измерения, вызванную допущением t  const , по сравнению с формулой
 aH 
p  p0 1 

T0 

Mg
Ra
. Температурный градиент a  0,006 K м , температура у поверхно-
сти Земли равна градуировочной.
Решение. По барометрической формуле p  p0 e

MgH
RT
. Используя условие за-
MgH
p0
 1,8  e RT . Логарифмируя последнее равенство и подставляя данp
ные задачи, получаем: n1,8  1, 23 104 H  H  4800 м .
дачи, имеем:
С учетом температурного градиента
 aH 
p0
 1,8  1  1 
p
T0 


Mg
Ra
. Отсюда
 aH 
 aH 
g1,8  5, 68 g 1  1   g 1  1   0, 0449  H1  4540 м .
T0 
T0 


Значит, относительная погрешность составит
H  H1
 5, 4% .
H
2.2. Основы термодинамики
2.2.1. Внутренняя энергия. Первое начало термодинамики
Рассмотрим теперь внутреннюю энергию тела.
Внутренней энергией тела называется энергия тела за вычетом кинетической энергии тела как целого и потенциальной энергии во внешнем поле сил.
(Например, внутренняя энергия газа в сосуде не включает кинетическую энергию
всего сосуда и его потенциальную энергию.) В понятие внутренней энергии
включается кинетическая энергия движения молекул (хаотического движения),
потенциальная энергия взаимодействия между молекулами и внутримолекулярная
энергия. Внутренняя энергия системы тел равна сумме внутренних энергий каждого из тел в отдельности (т. е. внутренняя энергия – величина аддитивная).
Внутренняя энергия – функция состояния системы. Каждый раз, когда система оказывается в данном состоянии, ее внутренняя энергия принимает присущее этому состоянию значение. Следовательно, изменение внутренней энергии
93
при переходе системы из одного состояния в другое будет всегда равно разности
значений внутренней энергии в тех состояниях независимо от пути, по которому
совершался переход.
Из опыта известно, что внутренняя энергия идеального газа зависит только
от температуры:
U  BT ,
где B – коэффициент пропорциональности, постоянный в широком интервале температур.
Внутренняя энергия может меняться за счет двух процессов: совершения
над телом работы А и сообщения телу тепла Q .
Если внешние тела совершают над системой работу A , то по третьему закону
Ньютона, система совершает над внешними телами работу А , причем А   А .
Сообщение системе тепла не связано с производством над ней макроскопической работы, т. е. с перемещением внешних тел. Изменение внутренней энергии
в этом случае обусловлено тем, что отдельные молекулы более нагретого тела совершают работу над отдельными молекулами тела, нагретого меньше. Совокупность микроскопических процессов, приводящих к передаче энергии от одного
тела к другому, называется теплопередачей.
Количество энергии, переданное от тела к телу путем теплопередачи, определяется количеством тепла Q , отданного одним телом другому.
Таким образом, приращение внутренней энергии системы должно быть равно сумме совершенной над системой работы А и количества сообщенного системе тепла Q :
U 2  U1  Q  A ,
где U1 ,U 2 – начальное и конечное значения внутренней энергии.
Обычно вместо работы А , совершенной внешними телами над системой,
рассматривают работу А , совершенную системой над внешними телами. Так как
А   А , то имеем Q  U 2  U1  A .
Это закон сохранения энергии. Он служит первым началом термодинамики,
которое формулируется следующим образом: «Количество тепла, сообщенное системе, идет на приращение внутренней энергии и на совершение системой работы
над внешними телами».
Первое начало термодинамики (как, впрочем, и другие начала) справедливо
только для очень медленно протекающих процессов. Поэтому при вычислении
совершенной системой работы или полученного системой тепла обычно разбивают рассматриваемый процесс на ряд элементарных процессов, каждый из которых
соответствует очень малому (в пределе – бесконечно малому) изменению параметров системы. Уравнение первого начала термодинамики для элементарного
процесса принимает вид: d Q  dU  d A .
Очень важно иметь в виду, что d Q и d A нельзя рассматривать как приращения величин Q и A . Соответствующее элементарному процессу изменение какой-либо величины можно считать приращением этой величины только в том
случае, если сумма этих изменений, соответствующая переходу из одного состоя94
ния в другое, не зависит от пути, по которому совершался переход, т. е. если данная величина является функцией состояния системы.
Рассмотрим цилиндрический сосуд с поршнем (рис. 2.2.1).
Рис. 2.2.1
Если газ под поршнем начнет расширяться, он будет перемещать поршень.
При перемещении поршня на расстояние dh совершится работа, равная d A  Fdh .
Так как F  PS , то d A  PSdh , но Sdh  dV . Отсюда d A  PdV . Значит, первое начало
термодинамики для элементарного процесса запишется в виде: d Q  dU  PdV .
2.2.2. Теплоемкость
Введем понятие теплоемкости. Теплоемкостью тела называется величина,
равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один кельвин:
Стела 
dQ  Дж 
.
dТ  К 
Дж 
Теплоемкость 1 моля вещества называется молярной теплоемкостью С 
.
 мольК 
Теплоемкость единицы массы вещества называется удельной теплоемкостью
 Дж 
.
с 
 кг  К 
Связь удельной и молярной теплоемкости очень проста c 
C
( М – моM
лярная масса).
Величина теплоемкости зависит от условий, при которых происходит
нагревание тела. Наибольший интерес представляют теплоемкости для случаев,
когда нагревание происходит при постоянном объеме или постоянном давлении.
В первом случае теплоемкость называется теплоемкостью при постоянном объеме
( CV ), во втором – теплоемкостью при постоянном давлении ( СP ).
Если нагревание происходит при постоянном объеме, тело не расширяется и
не производит работы над внешними телами. В соответствии с первым началом
термодинамики все тепло идет на приращение внутренней энергии:
dQ  dU  PdV ; PdV  0  dQV  dU .
(Штрих в выражении d Q будем опускать, помня о сказанном выше). Так
dQ
dU 
как CV    , то CV  
 .
 dT V
 dT V
95
Для идеального газа внутренняя энергия зависит только от Т , поэтому индекс V можно опустить: CV 
dU
dT
. Для получения молярной теплоемкости нужно
dU m
.
dT
Для одного моля U m  BmT . Отсюда dU m  Bm dT . Значит Bm  CV . Таким обра-
брать внутреннюю энергию одного моля CV 
зом, выражение для внутренней энергии одного моля идеального газа можно
представить в виде: U m  CV T .
С другой стороны, энергия одного моля идеального газа равна энергии одi
2
i
2
ной молекулы, умноженной на число молекул в моле: U m   N A  kTN A  RT .
i
2
Сравнивая два выражения для внутренней энергии, видим, что CV  R .
Для произвольной массы газа внутренняя энергия будет равна U m , умноженной на число молей газа m M :
U
m
m i
CV T 
RT .
M
M 2
Если нагревание газа происходит при постоянном давлении, то газ будет
расширяться, совершая над внешними телами работу. Следовательно, для повышения температуры газа на один кельвин в этом случае понадобится больше тепла, чем при нагревании при постоянном объеме, так как часть тепла будет затрачиваться на совершение газом работы. Поэтому теплоемкость при постоянном
давлении должна быть больше, чем теплоемкость при постоянном объеме.
По первому началу термодинамики для одного моля газа:
dQP  dU m  PdVm .
По определению теплоемкости CP 
dQP dU m
dU m
 dV 

 P  m  ; так как
 CV ,
dT
dT
dT
 dT  P
имеем CP  CV  P 
dVm 
 .
 dT  P
Из уравнения состояния идеального газа для одного моля PVm  RT имеем
Vm 
dV
R
RT
R
. Изменение объема будет равно dVm  dT , откуда  m   . Значит, для
P
P
 dT  P P
теплоемкости при постоянном объеме имеем:
CP  CV  R .
Это уравнение называется уравнением Майера. Из него видно, что работа,
которую совершает один моль идеального газа при повышении его температуры
на один кельвин при постоянном давлении, оказывается равной газовой постоянной R .
i
2
Учитывая, что СV  R , уравнение Майера можно переписать в виде:
Cp 
i2
R.
2
96
Пример 7. 2 л азота находятся под давлением р  105 Па . Какое количество
тепла надо сообщить азоту, чтобы: 1) при p  const объем V увеличить вдвое;
2) при V  const давление увеличить вдвое?
Решение. При постоянном давлении имеем: Q 
пейрона–Менделеева дает pV1 
m
pV
T 
M
R
чаем Q  CP
m
C p T . Но уравнение КлаM
m
m
RT1 и pV2 
RT2 . Отсюда pV 
M
M
m
M
RT или
. Учитывая, что для двухатомного азота СР  29,1 Дж  моль  К  , полуpV
 700 ( Дж ) .
R
m
CV T . Уравнение Клапейрона–
M
m
m
m
m
V p
Менделеева дает p1V  RT1 и p2V  RT2 , откуда V p  RT или
.
T 
M
M
M
M
R
V p
Следовательно, Q  CV
 500 ( Дж ) .
R
Пример 8. В закрытом сосуде объемом V  2 л находится азот, плотность
которого равна   1, 4 кг м3 . Какое количество тепла Q необходимо сообщить азо-
При постоянном объеме имеем Q 
ту, чтобы нагреть его в этих условиях на t  100 С ?
Решение. Внутренняя энергия азота в начальном состоянии U1 
конечном состоянии – U 2  2i
ема,
все
подводимое
m
RT2 .
M
тепло
i m
RT1 .
2M
В
Поскольку газ при нагревании не меняет объ-
идет
на
увеличение
внутренней
энергии:
i VR
T (учтено, что m  V ). Подставляя данные задачи, получаем:
2 M
Q  208 Дж .
Q  U 
2.2.3. Равновесные процессы
Любая система может находиться в различных состояниях, отличающихся
температурой, давлением, объемом и т. д. Эти величины называются параметрами системы. (Система – это совокупность рассматриваемых тел: например, вода и
пар.) Если системе нельзя приписать определенное значение какого-либо параметра, например, Т (температура в разных точках системы неодинакова), то состояние называется неравновесным. Если такое тело изолировать от других тел и
предоставить самому себе, то температура выровняется, тело перейдет в равновесное состояние. Это значение Т не изменится, пока система воздействием извне
не будет выведена из равновесного состояния.
Равновесным состоянием называется такое состояние системы, при котором
все параметры системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
97
Всякий процесс, т. е. переход из одного состояния в другое, связан с нарушением равновесия системы. Значит, при любом процессе система проходит через последовательность неравновесных состояний.
Рассмотрим сосуд с поршнем. Вдвигаем поршень быстро – равновесие сжимаемого газа нарушается (перед поршнем газ сжат, в дальних областях – нет);
вдвигаем поршень медленно – давление успевает выравниваться, а это значит, что
равновесие нарушается незначительно; вдвигаем поршень бесконечно медленно –
равновесие системы не нарушается. При бесконечно медленном сжатии газа в сосуде состояние газа в каждый момент времени будет равновесным.
Процесс, состоящий из непрерывной последовательности равновесных состояний, называется равновесным. Ясно, что равновесным может быть только
бесконечно медленный процесс. Реальные процессы при медленном протекании
могут приближаться к равновесным.
Равновесный процесс может быть проведен и в обратном направлении; при
этом система будет проходить через те же состояния в обратной последовательности. Вследствие этого равновесные процессы называются обратимыми.
Процесс, при котором система после ряда изменений возвращается в исходное состояние, называется круговым или циклом.
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров
состояния сохраняется постоянным.
2.2.4. Изопроцессы
Процесс, проходящий при неизменной температуре, называется изотермическим процессом. Этот процесс можно представить как медленно протекающий
процесс при хорошем теплообмене с окружающей средой, имеющей постоянную
температуру. При изотермическом процессе внутренняя энергия газа не меняется.
По первому началу термодинамики dQ  dU  PdV .
m
Cv dT  0 . Отсюда dQ  PdV  dA . Значит, вся теплота, сообщаемая
M
телу, идет на совершаемую им работу: Q  A . При расширении газа работа против
Но dU 
внешних сил совершается за счет подводимого тепла.
Процесс описывается законом Бойля – Мариотта: PV  const .
Найдем работу изотермического расширения газа. Учитывая, что P 
m RT
M V
,
получим
V2
V2
V1
V1
A   PdV 
m
 M RT
V
P
dV m
m

RT n 2 
RT n 1 .
V
M
V1 M
P2
Процесс, который происходит без теплообмена с окружающей средой,
называется адиабатическим. Поскольку теплообмен отсутствует, то dQ  0 . По
первому началу термодинамики, dQ  dU  dA  dU  dA . Работа, совершаемая
идеальным газом при адиабатическом расширении, происходит за счет уменьше98
ния внутренней энергии – газ охлаждается; а при сжатии газа работа переходит во
внутреннюю энергию – газ нагревается.
Найдем уравнение, связывающее параметры идеального газа при адиабатическом процессе. Используя выражения для внутренней энергии и работы, мы моm
Cv dT . Из уравнения
M
dV
dT R dV
Сv dT  RT
0

 0 . При
V
T Cv V
m RT
M V
жем записать: PdV  
Клапейрона–Менделеева P 
Отсюда
бесконечно малом изменении пара-
.
метров системы dT и dV левая часть последнего выражения есть полный диффе
R

ренциал d  nT 
nV   0 . Получаем
C
v


C p  Cv  R
следует,
что
Cp
Cv
 1
nT 
R
nV  const . Из уравнения Майера
Cv
R
R Cp


 1    1,
Cv
Cv Cv
где

Cp
Cv
.
Значит,
nT   1 nV  const . Потенцируя это выражение, получим: TV  1  const . Послед-
нее равенство есть уравнение адиабаты в переменных T ,V . Его называют также
уравнением Пуассона.
От переменных T ,V с помощью уравнения Клайперона–Менделеева можно
перейти к другим переменным T , P или P,V . В самом деле
PV 
m
M PV
m RT
RT  T 
;V 
M
m R
M P
.
Подставив в уравнение адиабаты поочередно значения T и V , получим
1
и TP   const . Константы во всех трех случаях, конечно же, разные.
Адиабата, построенная по уравнению PV   const на PV – диаграмме
(рис. 2.2.2), идет круче, чем изотерма ( PV  const ).
Это объясняется тем, что при адиабатическом сжатии увеличение давления
обусловлено не только уменьшением объема газа, как при изотермическом сжатии, но и повышением его температуры. При адиабатическом же расширении
происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

PV  const
Рис. 2.2.2
99
Вычислим работу, совершаемую газом в адиабатическом процессе. Количество работы, совершенной в адиабатическом процессе, равно убыли внутренней
m
Cv dT . Если газ адиабатически расширяется от объема V1 до объеM
ма V2 , то его температура уменьшается от Т1 до Т 2 , и работа расширения идеаль-
энергии dA  
T
2
m
m
ного газа равна A   Cv  dT  Cv T1  T2  . Используя уравнение Клапейрона–
M T1
M
Менделеева,
последнему
 1
A
 V 
PV
1 1
1   1 
  1   V2 

 RT m
1



1M

выражению
 1
 V 
1   1 
  V2 
можно
придать
вид:

.

Процесс изменения состояния газа, протекающий при постоянном объеме,
называется изохорическим. В таком процессе газ не совершает работы dA  0 , т. е.
вся полученная или отданная теплота идет на изменение внутренней энергии тела
dQ  dU 
m
Cv dT .
M
Процесс изменения состояния газа, протекающий при постоянном давлении, называется изобарическим. В этом процессе может меняться внутренняя
энергия и совершаться работа, т. е. первое начало термодинамики записывается в
виде: dQ  dU  dA . Так как dA  PdV , то работа газа при расширении объема от V1
V2
до V2 равна A   PdV  P V2  V1  . Используя уравнение Клапейрона–Менделеева,
V1
последнему выражению несложно придать вид: A 
m
R T2  T1  .
M
Такая работа бу-
дет совершена в изобарическом процессе при сообщении газу массой т количества теплоты dQ 
dU 
m
C p dT . При этом внутренняя энергия возрастает на величину
M
m
CV dT .
M
Пример 9. При изотермическом сжатии 2,8 кг окиси углерода объем его
уменьшается в четыре раза. Определить работу сжатия, если температура газа 7 С .
Решение. Работа при изотермическом сжатии равна: A 
V
m
RT n 2 . МолярM
V1
ная масса окиси углерода CO равна M  28 г моль  0, 028 кг моль .Используя дан2,8  8,31 280
n0, 25  322562( Дж) .
0, 028
Пример 10. Азот  N2  адиабатически расширяясь, совершает работу, равную
ные задачи, получим: A 
480 кДж . Определить конечную температуру газа, если до расширения он имел температуру Т1  362 К . Масса азота m  12 кг . Теплоемкость считать постоянной.
Решение. При адиабатическом расширении
T
A
2
m
m
Cv  dT  Cv T1  T2  .
M T1
M
100
Азот – двухатомный газ, т. е. СV  20,8 Дж  моль  К  . Молярная масса азота
М  0,028 кг моль . Выразив Т 2 и подставив данные задачи, получим: Т 2  308, 2 К .
2.2.5. Второе начало термодинамики
Первое начало термодинамики, выражая закон сохранения и превращения
энергии, не позволяет установить направление протекания термодинамических
процессов. Кроме того, можно представить множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются. Необходимость дать ответ на вопрос, какие процессы в природе
возможны, а какие – нет, привела к появлению второго начала термодинамики,
которое определяет направление развития процессов.
В естественных процессах превращения энергии и теплообмена есть определенная направленность: любые виды энергии превращаются в теплоту, а теплота, переходя от более нагретых тел к менее нагретым телам, рассеивается между
всеми окружающими телами. Эта теплота является потерянной.
Чем выше температура системы по отношению к температуре окружающих
тел, тем больше возможность полезного использования содержащейся в ней теплоты. Например, нетрудно превратить в работу теплоту, содержащуюся в нагретом до высокой температуры паре и практически невозможно использовать громадное количество теплоты, которое содержит вода морей и океанов при температуре, очень мало отличающейся от температуры окружающих тел. Для характеристики «качества» (если так можно выразиться) теплоты, а также для количественного учета обесценивания и рассеяния теплоты, происходящего в процессах
превращения энергии и теплообмена, в термодинамике используется величина,
называемая приведенным количеством теплоты или просто приведенной теплотой. Приведенной теплотой называется отношение теплоты, полученной или отданной в изотермическом процессе, к термодинамической температуре, при которой теплота отдается или получается: Qпр  Q T . (Теплота передается или получается без изменения температуры.)
Характерным является не абсолютная величина приведенной теплоты, а ее
изменение Qпр при тех или иных процессах. Если приведенная теплота возрастает, это значит, что возможности полезного использования теплоты уменьшились.
Если она уменьшается, то наоборот.
Пусть, например, некоторое количество теплоты dQ перешло от тела с более высокой температурой T1 к телу с более низкой температурой T2 (будем считать, что температуры тел при этом не изменились). При этом приведенная теплота первого тела уменьшилась на Qпр 
dQ
, а приведенная второго тела увеличилась
T1
dQ
. Но T2  T1 , значит, Qпр  Qпр . Отсюда следует, что приведенная теплота
T2
dQ dQ

обоих тел (суммарная) увеличилась на dQпр  Qпр  Qпр 
. Произошло рассеT2
T1
на Qпр 
101
яние теплоты, и возможности полезного использования данного количества теплоты dQ уменьшились.
Если процесс неизотермический, то его можно разбить на малые участки, на
которых тело получает теплоту dQ при практически постоянной температуре. Тогда приведенная теплота будет равна Qпрi  dQi Ti ( Ti – температура, при которой
тело получает тепло dQi ).
Переход тела из данного состояния в другое может произойти бесчисленным количеством способов; при этих переходах тело может получить самые различные количества тепла. Но при этом сумма приведенных теплот

i
иметь одно и то же значение. Значит, интеграл
dQi
будет
T
2
dQ
не зависит от пути, по котоT
1

рому тело переходило из состояния 1 в состояние 2, и его можно рассматривать
как разность значений некоторой функции в состояниях 2 и 1 данного тела
2
dQ
. Эта функция S называется энтропией. Энтропия является одной из
1 T
S2  S1  
важных характеристик состояния термодинамической системы и служит мерой
обесценивания теплоты, которое имеет место при различных энергетических процессах и теплообмене.
Из данного определения энтропии ясно, что изменение ее при круговом обратимом процессе (цикле) в замкнутой системе равно нулю. Напомним, что обратимый процесс – это процесс, который может самопроизвольно протекать как в
прямом, так и в обратном направлениях. В замкнутой системе обратимым может
быть только идеальный процесс, не сопровождающийся никакими потерями. Энтропия при таком процессе не меняется: S  const , S  S2  S1  0 .
Необратимый процесс может самопроизвольно протекать только в одном
направлении. Все реальные процессы превращения энергии, протекающие в замкнутой системе, необратимые. Энтропия в таких процессах увеличивается.
Проще всего энтропия выражается при изотермическом процессе:
dS  S2  S1  Q T . При неизотермическом процессе можно разбить процесс на элементарные участки (бесконечно малые) и изменение энтропии вычислить как
сумму: dS  
i
dQi
.
Ti
Если известно уравнение состояния, то энтропия может быть вычислена очень
просто. По определению, dS  dQ T . По первому началу термодинамики,
m
m
dT
dV
. Из уравнения Клапейрона–
Cv dT  PdV . Отсюда dS 
Cv
P
M
M
T
T
m
m RT
Менделеева PV  RT выразим давление: P 
и подставим в выражение для энM
M V
m
dT m dV
тропии: dS  Cv
. Правая часть последнего равенства является полным

R
M
T
M V
m
m
m
m
дифференциалом от выражения  Cv nT  R nV  , т. е. dS  d  Cv nT  R nV  .
M
M
M

M

dQ  dU  dA 
102
Интегрируя, получаем: S2  S1 
m
M

T2
V2 
 Cv n  R n  (индекс 1 – начальное состояние,
T1
V1 

индекс 2 – конечное).
Обратимых процессов, строго говоря, не существует, хотя можно осуществить великое множество процессов, практически неотличимых от обратимых.
Все зависит от времени релаксации – так называется время, в течение которого
устанавливается равновесие. Это время в различных процессах может меняться от
ничтожных долей секунды (время выравнивания давления в однородном газе 
1016 с ) до времени, измеряемого неделями (перемешивание разнородных веществ). Предположим, что мы сжимаем газ и весь процесс занимает одну секунду.
Время релаксации 1016 с . Поэтому мы вправе считать, что этот реальный процесс
есть последовательность равновесных состояний, т. е. обратимый процесс.
Однако в природе есть всегда односторонние процессы, и уже поэтому они
никоим образом не могут быть обращены. Например, газ может расширяться сам
по себе, но не может сжиматься без приложения внешних сил. Тепло может самопроизвольно переходить от горячего тела к холодному и только при затрате работы (например, электроэнергии) может переходить от холодного тела к более
нагретому. При трении кинетическая энергия макроскопического движения всегда превращается во внутреннюю энергию, но никогда не происходит самопроизвольный обратный процесс.
Необратимость всех остальных процессов в конечном счете связана с тем,
что в каждом из них в той или иной мере присутствует один из перечисленных
односторонних процессов. В реальных процессах невозможно избежать ни самопроизвольных расширений, ни трения, ни теплового рассеяния.
Тепловое рассеяние. В случае теплообмена между двумя телами общее (всей
системы) изменение энтропии равно dS 
Q1 Q2

( Q1 – тепло, полученное более
T1 T2
холодным телом с температурой Т1 ; Q2 – тепло, потерянное более горячим телом с
температурой T2 ). Тепло, сообщенное телу, считается положительным. Поскольку
в процессе участвует одно и то же количество теплоты, то Q1  Q2  Q и
1 1
dS  Q     0 , так как T2  T1 , т. е. при тепловом обмене общая энтропия систе T1 T2 
мы, в которой произошел теплообмен, возрастает.
Трение. Внутри сосуда с газом происходит интенсивное механическое движение (например, вертится колесо). Объем не меняется, температура растет, поT
V
m
(Cv n 2  R n 2 )
M
T1
V1
V
T
m
S  Cv n 2  0 , т. е. возрастет (объем не меняется, n 2  0 ).
V1
M
T1
этому энтропия ( в соответствии с S2  S1 
изменится на
Расширение газа. При расширении в пустоту при неизменной температуре
прирост энтропии S2  S1 
V
m
R n 2  0 , т. е. опять положительный.
M
V1
103
Итак, во всех односторонних процессах энтропия системы возрастает. Так
как все необратимые процессы сопровождаются этими односторонними явлениями, идущими с повышением энтропии, то прирост энтропии у необратимого процесса будет завышен относительно того прироста, который имел бы место при
обратимом переходе. Пусть dQ – тепло, полученное телом при температуре T в
обратимом процессе; прирост энтропии равняется при этом dQ T ; в реальном
процессе прирост энтропии будет больше этой величины: dS  dQ T . Если система
теплоизолирована (процессы в ней адиабатические), то dQ  0 и для обратимого
процесса dS 
dQ
 0 ; для необратимого же процесса всегда dS  0 .
T
Значит, можно утверждать: энтропия теплоизолированной системы возрастает или остается постоянной. Это и есть второе начало термодинамики.
Поскольку все реальные процессы необратимы, в теплоизолированной системе возможны лишь процессы, идущие с возрастанием энтропии. Поэтому второе
начало можно сформулировать так: все реальные процессы превращения энергии в
замкнутой системе протекают так, что общая энтропия системы увеличивается.
В нетеплоизолированной системе при получении системой тепла в обратимом процессе dS  dQ T ; в необратимом процессе dS  dQ T . Объединяя эти формулы, получим dS  dQ T (для теплоизолированной системы dS  0 ).
Следует помнить, что нетеплоизолированная система может обмениваться теплом с окружающей средой, поэтому ее энтропия может вести себя любым способом.
Равновесному состоянию замкнутой системы при этом соответствует максимально возможная энтропия: S равн  S макс . Вся энергия системы при этом переходит в теплоту, равномерно рассеянную между телами системы. Таким образом, не
вся внутренняя энергия системы может быть полезно использована в реальных
условиях для превращения ее в работу; часть ее, обусловленная изменением энтропии dQ  TdS , будет потеряна. Та часть внутренней энергии, которая может
быть превращена в работу, называется свободной энергией системы F и может
быть найдена из соотношения: F  U  TdS .
С молекулярно-кинетической точки зрения термодинамическая система
(например, идеальный газ) представляет собой объединение громадного числа отдельных молекул. Макропараметры этого объединения (температура, давление и
т. п.) обусловливаются микросостояниями отдельных молекул (т. е. зависят от кинетической энергии молекул, распределения их в объеме, занимаемом системой и
т. д.). При этом одни и те же макропараметры системы могут обеспечиваться при
различных микросостояниях отдельных молекул. Число таких микросостояний,
возможных при данных макропараметрах системы, называется статистическим
весом данного состояния системы.
Больцман установил соответствие между энтропией S и статистическим весом W : S  k nW ( k – постоянная Больцмана).
Состояние системы, которое не имеет тенденции к изменению с течением
времени, – равновесное состояние. Понятно, что отсутствие такой тенденции будет сильнее всего выражено у наиболее вероятного из всех макросостояний. Вероятность макросостояния пропорциональна его статистическому весу. Поэтому
104
равновесное состояние изолированной системы можно определить как состояние,
статистический вес которого максимален.
С такой точки зрения энтропия может рассматриваться как мера статистического веса системы; второе начало термодинамики в этом случае может быть
сформулировано так: все естественные процессы в замкнутой термодинамической
системе протекают так, что система переходит от состояний менее вероятных к
состояниям более вероятным.
При абсолютном нуле ( T  0K ) всякое тело (за редким исключением) находится в состоянии, статистический вес которого равен 1 ( W  1). В этом случае
S  k nW  0 , т. е. определение энтропии, по Больцману, приводит к нулевому значению энтропии. Отсюда вытекает, что энтропия всякого тела стремится к нулю
при стремлении к нулю температуры: im S  0 .
T 0
Это утверждение представляет собой содержание так называемой теоремы Нернста. Иногда его называют третьим началом термодинамики. Эта теорема дополняет
первые два начала термодинамики сведениями о поведении систем при нуле Кельвина.
Пример 11. Найти изменение энтропии при превращении 10 г льда при
20 С в пар при 100 С .
Решение. Изменение энтропии при переходе тела из одного состояния в другое
2
dQ
, где S1 и S 2 – значения энтропии в первом и во втором состояни1 T
равно: S2  S1  
ях. Общее изменение энтропии в нашем случае складывается из изменений ее в отдельных процессах. В первом процессе лед массы т нагревается от температуры Т1
до температуры Т 2 . По уравнению теплового баланса имеем: dQ  mc1dT ( c1 – удельная теплоемкость льда). Подставляя это в выражение для изменения энтропии, получаем: S1  mc1 n T2 T1  . Во втором процессе происходит плавление льда массы т при
температуре Т 2 . Процесс изотермический: S2  Q T2 , где Q  m – теплота, затраченная на плавление (  – удельная теплота плавления). Таким образом, S2   m  T2 .
Третий процесс – нагревание воды массой т до температуры Т 3 (до кипения). Этот
процесс аналогичен первому: S3  mc2 n T3 T2  . Здесь c2 – удельная теплоемкость воды. Четвертый процесс – испарение – идет при постоянной температуре Т 3 и аналогичен второму процессу: S4   mr  T3 . Здесь r – удельная теплота парообразования.
Общее изменение энтропии

T
T 
r 
S  m  c1 n 2   c2 n 3   .
T1 T2
T2 T3 

По условию задачи:
m  0, 01кг; с1  2,1 103 Дж  кг  К  ; Т1  253 К ;
Т 2  273К ; Т 3  373К ;   3,35105 Дж кг;
с2  4,19 103 Дж  кг  К  ; r  2, 26 106 Дж кг.
Подставив эти данные в выражение изменения энтропии, получим:
S  88 Дж К .
105
2.2.6. Тепловые машины. Цикл Карно
На PV -диаграмме круговой процесс (цикл) изображается замкнутой кривой.
Весь цикл можно представить как последовательность процессов сжатия и расширения (рис. 2.2.3): рабочее тело, например, идеальный газ, сначала расширяется
от объема V1 до объема V2 , затем сжимается от V2 до V1 . Очевидно, что работа
расширения положительна ( dV  0  A   pdV  0 ) и определяется площадью под
кривой расширения, работа сжатия – отрицательна.
Рис. 2.2.3
Знак суммарной работы цикла зависит от того, какая из этих работ больше,
т. е. в каком направлении проходит цикл – по часовой стрелке или против. Если
суммарная работа положительна, цикл называется прямым (рис. 2.2.3 а); в противном случае цикл называется обратным (рис. 2.2.3 б).
В результате цикла рабочее тело возвращается в исходное состояние. Значит, изменение его внутренней энергии равно нулю: dU  0 . Работа, произведенная рабочим телом, совершается за счет полученной извне теплоты: A  Q .
Но в процессе цикла рабочее тело может как получать теплоту, так и отдавать ее. Отсюда следует, что Q  Q1  Q2 , где Q1 и Q2 – количества теплоты, полученной и отданной рабочим телом в процессе цикла. Отношение работы, совершенной в процессе цикла, к количеству теплоты, полученной рабочим телом за
цикл, называется термическим коэффициентом полезного действия:

Q
A Q1  Q2

 1 2 .
Q1
Q1
Q1
Во всех тепловых машинах осуществляется круговой процесс, т. е. цикл: в
тепловых двигателях используется прямой цикл, в холодильных машинах – обратный. Из второго начала термодинамики следует, что в замкнутых системах все
реальные процессы идут с повышением энтропии, т. е. часть полученной рабочим
телом теплоты с необходимостью должна рассеяться (должна быть передана каким-либо другим телам). Значит, работа любой тепловой машины требует наличия двух сред (термостатов) с разной, но постоянной температурой. Например, в
тепловых двигателях из термостата с более высокой температурой (нагревателя)
рабочее тело получает теплоту, термостату с более низкой температурой (холодильнику) – отдает часть полученной теплоты; полезная работа совершается за
счет разности полученной и отданной теплоты: A  Q1  Q2 . Для того чтобы терми106
ческий коэффициент теплового двигателя был равен   1 , должно быть Q2  0 , а
это невозможно.
В холодильных машинах используется обратный цикл. Рабочее тело от термостата с более низкой температурой Т 2 забирает количество теплоты Q2 и отдает
термостату с более высокой температурой T1 количество теплоты Q1 . Работа производится за счет разности полученной и отданной теплоты A  Q  Q2  Q1  0 . В
холодильных машинах производится отрицательная работа и Q1  Q2  A . Отданное
количество теплоты больше полученного на величину работы, совершенной над
системой. Следовательно, без совершения работы нельзя отобрать тепло от менее
нагретого тела и отдать его более нагретому.
Обратный цикл Карно лежит в основе действия тепловых насосов. В отличие от холодильных машин тепловые насосы предназначены для передачи больших количеств тепловой энергии горячему телу, например, системе отопления.
Часть этой энергии отбирается от окружающей среды с низкой температурой, а
часть – получается за счет механической работы компрессора.
Французский физик Карно проанализировал работу тепловых машин и доказал, что наиболее экономичным циклом является обратимый цикл, состоящий
из двух изотерм и двух адиабат. Рассмотрим прямой цикл Карно с идеальным газом в качестве рабочего тела.
На рис. 2.2.4 изотермические расширение и сжатие изображены, соответственно, кривыми 1–2 и 3–4, а адиабатические расширение и сжатие – кривыми 2–3 и 4–1.
Рис. 2.2.4
При изотермическом процессе U  const , значит, полученная теплота идет на
работу расширения: A12 
тепла
A23  
нет,
и
работа
V
m
RT1 n 2  Q1 . При адиабатическом расширении притока
M
V1
совершается
за
счет
убыли
внутренней
энергии:
m
CV T2  T1  . Количество тепла, отданное рабочим телом термостату с низкой
M
температурой,
при
изотермическом
сжатии,
равно
работе
сжатия:
V
m
m
A34 
RT2 n 4  Q2 . Работа адиабатического сжатия равна A41   CV T1  T2    А23 .
M
V3
M
Работа цикла составит:
A  A12  A23  A34  A41  Q1  A23  Q2  A23  Q1  Q2 .
107
Термический к. п. д. такого цикла равен:   A Q1  Q1  Q2  Q1 . Используя
уравнение адиабаты TV  1  const , выражение для термического к. п. д. легко преобразовать к виду:   Т1  Т 2  Т1 . Отсюда видно, что к. п. д. определяется только
температурами используемых термостатов: для его повышения необходимо увеличивать разность температур термостатов.
Пример 12. Теплосиловая установка работает по циклу Карно. Определить к. п.
д. установки, если температура нагревателя 600 С , а температура холодильника 15 С .
Решение. К. п. д. тепловой машины, работающей по циклу Карно, равен
  1  T2 T1 . Подставляя данные задачи, получаем:   0, 67 .
Пример 13. Доказать, что изменение температуры холодильника сильнее
сказывается на к. п. д. цикла Карно, чем такое же изменение температуры нагревателя.
Решение. К. п. д. цикла Карно   1 
T2
. Скорость изменения функции при
T1
изменении аргумента есть первая производная функции по этому аргументу:
 T2 T1  T2 
 T2 T1 
T

1



 2;

    12 . Так как T1  T2 , то
.

T1
T1
T1 T2
T2
T1
T1
T2 T1
2.3. Агрегатные состояния вещества
При рассмотрении реальных газов необходимо учитывать, что между молекулами существуют силы межмолекулярного взаимодействия, которые проявляются
при сближении молекул на очень малые расстояния   109 м  : сначала преобладают
силы притяжения, но при дальнейшем сближении – силы отталкивания. Системы взаимодействующих молекул обладают потенциальной энергией взаимодействия, принимающей минимальное значение при расстоянии между молекулами, на котором
силы притяжения и силы отталкивания уравновешивают друг друга.
Кроме потенциальной энергии системы реальных молекул, участвующих в тепловом движении, обладают кинетической энергией. Соотношение между потенциальной и кинетической энергиями системы молекул определяет агрегатное состояние
вещества. Если Ек  ЕПмин , вещество находится в газообразном состоянии. Если
Ек  ЕПмин , вещество находится в твердом состоянии. Если Ек  ЕПмин , состояние вещества – жидкое.
2.3.1. Ван-дер-ваальсовский газ
Уравнение состояния идеального газа удовлетворительно описывает поведение
реальных газов только при низких давлениях и достаточно высоких температурах.
С повышением давления и понижением температуры наблюдаются значительные отступления от уравнения Клапейрона–Менделеева: pVm  RT .
Для описания поведения реальных газов в широком интервале плотностей
было предложено много различных уравнений. Самым простым из них и вместе с
тем дающим достаточно хорошие результаты оказалось уравнение Ван-дер108
Ваальса. Это уравнение было получено путем внесения поправок в уравнение
Клапейрона–Менделеева:

a 
 p  2  Vm  b   RT .
Vm 

Здесь a и b – константы Ван-дер-Ваальса, определяемые опытным путем.
Из-за взаимного притяжения между молекулами (сил Ван-дер-Ваальса) газ
как бы сжимается бо льшим давлением, чем давление р , оказываемое на газ
стенками сосуда, в котором он заключен. Поправка в первом множителе уравнения Ван-дер-Ваальса характеризует ту добавку, которая обусловлена взаимным
притяжением молекул друг к другу.
Вследствие того что молекулы обладают конечным объемом, пространство, доступное для движения молекул, оказывается меньшим, чем объем сосуда Vm . Поправка b характеризует ту часть объема, которая недоступна для движения молекул.
Уравнение Ван-дер-Ваальса, приведенное выше, написано для одного моля
газа. Чтобы перейти к уравнению для произвольной массы газа т необходимо
учесть, что  молей газа при тех же условиях занимают в  раз больший объем:
V   Vm . Подставив в уравнение Ван-дер-Ваальса Vm  V  , получим:

 2a 
 p  2  V  b    RT .
V 

Реальные газы следуют уравнению Ван-дер-Ваальса лишь приближенно.
Воображаемый газ, точно подчиняющийся этому уравнению, называется ван-дерваальсовским.
Внутренняя энергия ван-дер-ваальсовского газа должна включать в себя,
кроме кинетической энергии молекул, потенциальную энергию взаимодействия
между молекулами. Кинетическая энергия молекул – это внутренняя энергия идеального газа CV T . Для нахождения потенциальной энергии взаимодействия молекул учтем, что работа, совершаемая при расширении газа против сил взаимного
притяжения молекул друг к другу, равна изменению энергии взаимодействия
d A  dEП . В уравнении Ван-дер-Ваальса давление, обусловленное силой взаимного притяжения между молекулами, учтено добавкой р  a Vm2 . Соответственно,
работа против сил взаимного притяжения между молекулами равна
d A   a Vm2  dV  dE П . Интегрирование последнего равенства дает: ЕП   а Vm  const .
Константу можно положить равной нулю. Тогда внутренняя энергия одного моля
ван-дер-ваальсовского газа определится выражением:
U m  CV T  a Vm .
Внутренняя энергия  молей газа будет в  раз больше.
Уравнение Ван-дер-Ваальса удовлетворительно описывает поведение реального газа при изотермическом сжатии, кроме состояния, в котором сосуществуют две фазы: газобразная и жидкая.
Несколько различно ведут себя идеальный и реальный газы при адиабатическом расширении. Идеальный газ при адиабатическом расширении в пустоту работы
109
не совершает и поэтому его внутренняя энергия не меняется. Из этого следует, что
при подобном расширении температура идеального газа остается постоянной.
Английские физики Джоуль и Томсон показали, что при адиабатическом
расширении реального газа постоянной остается величина U  pV  const , называемая энтальпией. Отсюда ясно, что в подобном процессе внутренняя энергия и, соответственно, температура могут меняться. Изменение температуры реального газа в результате его адиабатического расширения называется эффектом Джоуля–
Томсона. Если температура газа снижается, эффект считается положительным, в
противном случае – отрицательным.
Эффект Джоуля–Томсона является следствием отклонения реального газа
от идеальности и в зависимости от условий процесса может быть как положительным, так и отрицательным.
Положительный эффект Джоуля – Томсона используется в некоторых установках по сжижению газов. Так как газ сжижается при температурах ниже критической, его охлаждение достигается путем многократного повторения процесса
адиабатического расширения.
Пример 1. Для некоторого газа поправка в уравнении Ван-дер-Ваальса
а  45,3 104 Н  м4 кмоль2 , а критическая температура Т кр  282, 7 К . Определить эффективный диаметр молекулы газа, полагая, что поправка Ван-дер-Ваальса на
объем молекул b  4Vэф N A , где Vэф – эффективный объем одной молекулы.
Решение.
2
2
2
2
27 Т кр R
27 Т кр R
а
 ркр 
 51, 4 105 Па;
64 pкр
64 a
b
Tкр R
8 pкр
 0, 0573 м3 кмоль .
1
6
Эффективный объем одной молекулы равен Vэф   3 , где  – эффективный
4
6
диаметр молекулы. Отсюда b   3 N A    3
3b
 3,5 1010  м  .
2 N A
Пример 2. Какую температуру имеют 2 г азота, занимающего объем 820 см3
при давлении 2 атм ? Газ рассматривать как 1) идеальный, 2) реальный.
Решение. Решая уравнение Клапейрона–Менделеева относительно температуры,
находим, что T 
MpV
mR
. По условию задачи
р  2атм  2, 026 105 Па; V  8, 2 104 м3 ;
т  2 103 кг; М N2  0, 028 кг моль
.
Отсюда Т  280 К .
Решая уравнение Ван-дер-Ваальса для произвольной массы газа относительно температуры, находим:
T
M 
am2  
m
p

V

2 2 
mR 
M
M V 

b.

Подставив в формулу числовые данные, получим с точностью до трех значащих цифр Т  280 К .
Таким образом, при невысоких давлениях газ ведет себя как идеальный.
110
2.3.2. Критическое состояние
Рассмотрим процесс изотермического сжатия вещества. Первоначально вещество – газообразное (рис. 2.3.1). При уменьшении объема давление газа будет расти.
При достижении объема VГ давление перестает меняться, а вещество перестает быть
однородным – часть газа конденсируется в жидкость, происходит расслоение на две
фазы.
Рис. 2.3.1
По мере дальнейшего уменьшения объема все большая часть вещества переходит в жидкую фазу, причем переход осуществляется при постоянном давлении (давлении насыщенного пара). Когда процесс конденсации заканчивается, что происходит
при достижении объема VЖ , дальнейшее уменьшение объема сопровождается быстрым ростом давления. На диаграмме pV состояниям равновесия между жидкостью и
насыщенным паром соответствует горизонтальный участок изотермы. Это общий результат для всех двухфазных состояний. Концы этого участка отвечают объемам VГ и
VЖ , занимаемым веществом в газообразной и жидкой фазах.
Если провести несколько аналогичных изотерм, то увидим, что с повышением температуры горизонтальный участок изотермы сокращается, стягиваясь в
точку при температуре Т кр , называемой критической (рис. 2.3.2). Сокращается
различие в плотностях жидкости и насыщенного пара. При критической температуре исчезает всякое различие между жидкостью и паром.
Рис. 2.3.2
Точка К , являющаяся пределом, к которому приближаются горизонтальные
участки изотерм при Т  Т кр , называется критической точкой, а состояние вещества,
111
изображаемое этой точкой, – критическим состоянием. Давление, объем и температура, соответствующие этой точке, также называются критическими.
Давление насыщенного пара растет с температурой, достигая при Т  Т кр
значения ркр . При Т  Т кр понятие насыщенного пара теряет смысл. Колоколообразная кривая, проведенная через концы горизонтальных участков, ограничивает
область двухфазных состояний вещества. При Т  Т кр вещество оказывается однородным. При таких температурах никаким сжатием ожижение вещества осуществлено быть не может.
2.3.3. Изотермы Ван-дер-Ваальса
В п. 2.3.1. было приведено уравнение, предложенное Ван-дер-Ваальсом, для
описания состояния газа, отличающегося от идеального. Однако изотермы Ван-дерВаальса, т. е. кривые зависимости p V  , построенные по уравнению

a 
 p  2  Vm  b   RT для фиксированных значений температуры, отличаются от реVm 

альных изотерм (рис. 2.3.3).
Рис. 2.3.3
Уравнение Ван-дер-Ваальса довольно хорошо описывает ход изотермы при
объемах, больших VГ . При объемах, меньших VЖ , ход реальной изотермы также
примерно следует приведенному выше уравнению. Таким образом, уравнение
описывает не только газообразное, но и жидкое состояния вещества.
При высоких температурах изотермы Ван-дер-Ваальса практически не отличаются от изотерм идеального газа. Решение уравнений Ван-дер-Ваальса для
критической изотермы (Т  Т кр ; р  ркр ) позволяет установить связь между критическими параметрами и константами Ван-дер-Ваальса:
Vкр  3b , ркр  а  27b 2  , Tкр  8a  27 Rb  .
Характерным отличием является то, что при температурах, не превышающих Т кр ,
у изотерм Ван-дер-Ваальса имеется S-образный завиток, в области которого заданному
значению давления соответствуют три различных значения объема (рис. 2.3.4)
У реальных изотерм такого завитка нет. Изотерма Ван-дер-Ваальса и реальная изотерма, совпадая на участках, отвечающих однофазным состояниям вещества, ведут себя совершенно различно в области расслоения вещества на две фазы.
112
Расслоение на две фазы объясняется неустойчивостью однородных состояний,
отвечающих завитку 1–2–3–4. Неустойчивость состояния на участке 2–3 очевидна:
сжатие вещества приводит к уменьшению давления; на практике же такие состояния
не реализуются. На участках 1–2 и 3–4 давление с ростом объема уменьшается, и при
определенных условиях такие состояния могут осуществиться. Вещество в состоянии
1–2 называется перегретой жидкостью; в состоянии 3–4 – пересыщенным паром. Эти
состояния очень не устойчивы.
Рис. 2.3.4
При достаточно низких температурах нижняя часть завитка изотермы Ван-дерВаальса пересекает ось V и переходит в область отрицательных давлений (рис. 2.3.4).
Вещество под отрицательным давлением, очевидно, находится в состоянии растяжения. Такие состояния при определенных условиях могут реализоваться.
Пример 1. Определить давление, при котором должен находиться 1 кмоль
азота, чтобы при Т  310 К он занимал объем равный 2,5м3 . Критические величины для азота равны: ркр  33,9 105 Па; Т кр  126,1 К .
Решение. Поправки Ван-дер-Ваальса:
b
Tкр R
8 ркр
 3,86 10 м моль ; a 
5
3
2
27 Tкр R
 0, 0164 Па  м 2 .
64 pкр

a 2 
Уравнение Ван-дер-Ваальса для  молей:  p  2  V  b    RT . Отсюда
V


6
 RT a
1000  8,31 310
0,0164 10
p
 2 

 1,044 106  Па  .
5
V  b V
2,5  1000  3,86 10
6, 25
2
2.4. Физическая кинетика
Знакомство с молекулярной физикой мы завершим небольшим экскурсом в
термодинамику неравновесных процессов.
113
Статистическая физика (м-к. т.) имеет дело с равновесными состояниями и
обратимыми процессами. Наука, изучающая процессы, возникающие при нарушении равновесия, называется физической кинетикой.
При нарушениях равновесия система стремится вернуться в равновесное состояние. Стало быть, в этом процессе энтропия возрастает и, значит, процесс необратим.
Нарушение равновесия сопровождается возникновением потоков либо молекул, либо тепла, либо зарядов и т. п. Эти процессы носят название явлений переноса и являются необратимыми процессами.
Классическими примерами явлений переноса являются диффузия, теплопроводность и внутреннее трение. При диффузии переносятся молекулы (т. е. вещество), при теплопроводности возникает поток тепла, при вязком трении передается импульс.
2.4.1. Диффузия
Явление диффузии заключается в том, что происходят самопроизвольное
проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей
и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает
и продолжается, пока существует градиент плотности, т. е. пока плотность распределена по суммарному объему двух тел неравномерно.
Во время становления молекулярно-кинетической теории по вопросу диффузии возникали противоречия. Так как молекулы движутся с огромными скоростями (порядка нескольких сотен метров в секунду), диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом
(например, флакон с духами), то запах распространяется довольно медленно. Однако противоречия здесь нет: молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном
«стоят» на месте.
Пусть в единице объема двухкомпонентной газовой смеси содержится n1
молекул одного вида и n2 молекул другого вида. Полное число молекул в единице
объема n  n1  n2 . Отношение ci  ni n называется относительной концентрацией
молекул этого вида.
Если в направлении какой-либо оси Z создаются градиенты концентраций
dc1 dZ и dc2 dZ и при этом dc1 dZ   dc2 dZ , то градиент суммарной концентрации
будет равен нулю: dc1 dZ  dc2 dZ  d  c1  c2  dZ  1 n  dn dZ  0 . Отсюда n = const. Более
того, давление тоже постоянно (это следует из уравнения Клапейрона–Менделеева:
p  nkT ). Поэтому газодинамические потоки не возникают (нет перепада давления).
Но тепловое движение молекул имеется всегда, и поэтому будет происходить процесс
выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания ее концентрации. Это и есть диффузия.
Таким образом, диффузией называется обусловленное тепловым движением
молекул самопроизвольное выравнивание концентраций в смеси нескольких различных веществ.
114
Введем понятие потока физической величины. Количество какой-либо величины, проходящее в единицу времени через некоторую поверхность, называется потоком этой величины (например, поток жидкости через сечение трубы, поток
света через оконное стекло и т. п.).
Опытным путем установлено, что поток молекул i -го вида через перпендикулярную к оси Z поверхность S определяется выражением:
Ni   D  dni dZ  S ,
где D – коэффициент диффузии. Если dni dZ  0 (концентрация молекул i -го
вида растет в направлении оси Z ), то поток будет величиной отрицательной. Значит,
молекулы переносятся против оси Z (рис. 2.4.1). В случае dni dZ  0 поток будет положительным (молекулы перемещаются в направлении оси Z ).
Рис. 2.4.1
Из приведенной формулы можно определить размерность коэффициента
диффузии. Размерность потока N i (число частиц в единицу времени) есть T 1 ;
размерность концентрации ni (число частиц в единице объема) есть L3 ; площадь
S имеет размерность L2 ; dZ – имеет размерность L . Отсюда D   N i  dni dZ  S  ,
т. е. размерность коэффициента диффузии будет равна L3 L TL2   L2 T  L2T 1.
Если выражение для потока молекул умножить на массу молекулы i -го вида
mi , то получим выражение для потока массы i -й компоненты: M i  D  d  dt  S . Здесь
M i  Ni mi – масса N i молекул; i  ni mi – парциальная плотность i -й компоненты.
Выражения для потока молекул и потока массы представляют собой эмпирические уравнения диффузии и называются законом Фика.
Молекулярно-кинетическая теория позволяет получить выражение для коэффициента диффузии: D  1 3 v  . Здесь v – среднеквадратичная скорость теплового движения молекул;  – средняя длина свободного пробега молекул.
2.4.2. Теплопроводность
Рассмотрим теперь перенос тепла (теплопроводность). Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений происходит процесс выравнивания средних кинетических энергий молекул, иными словами, выравнивание
температур. Опыт показывает, что при градиенте температуры dT dZ вдоль оси Z
115
возникнет
поток тепла, величина которого определяется формулой:
q    dT dZ  S .
Здесь q – поток тепла через поверхность S , перпендикулярную оси Z . Размерность потока тепла Дж с  Вт . Значит,  имеет размерность Вт  м  К  . Знак
минус в выражении для потока тепла отражает то обстоятельство, что тепло течет в
направлении убывания температуры. Поэтому знаки q и dT dZ противоположны.
Формула для потока тепла – это эмпирическое уравнение теплопроводности. Его называют законом Фурье.
Для коэффициента теплопроводности молекулярно-кинетическая теория дает выражение  
1
v  cV  .
3
Здесь v – среднеквадратичная скорость молекул;  –
плотность газа; cV – удельная теплоемкость при постоянном объеме;  – средняя
длина свободного пробега молекул.
Коэффициент теплопроводности газа не зависит от числа молекул в единице объема (т. е. от концентрации n ), а следовательно, и от давления  p  nkT  . Это
обусловлено следующими причинами. С понижением давления уменьшается n ,
т. е. число молекул, участвующих в переносе энергии. Одновременно растет  , а
значит, и различие в энергиях, переносимых молекулами в противоположных
направлениях (чем больше число столкновений между молекулами, тем больше
вероятность того, что энергии, переносимые одной молекулой в прямом и обратном направлениях одинаковы). В итоге получается, что количество энергии, переносимой молекулами при данном градиенте температуры, не зависит от давления.
Это справедливо лишь до тех пор, пока  остается малой по сравнению с расстояниями между поверхностями, обменивающимися теплом за счет теплопроводности заключенного между ними газа (например, по сравнению с размерами зазора
между внутренней и внешней колбами стеклянного термоса). По мере того, как
перестает выполняться это условие, теплопроводность начинает все больше зависеть от давления, уменьшаясь с его понижением. При  , превышающей расстояние между поверхностями, пробег молекул определяется величиной этого расстояния и перестает зависеть от давления. Число же молекул в единице объема n при
уменьшении давления продолжает убывать, вследствие чего уменьшается и коэффициент теплопроводности  . При повышении температуры коэффициент
теплопроводности растет.
2.4.3. Вязкое трение
Механизм возникновения внутреннего трения между параллельными слоями
газа (или жидкости), движущимися с различными скоростями, заключается в том, что
из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а импульс
слоя, движущегося медленнее, увеличивается; это приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
116
Сила внутреннего трения между двумя слоями газа (или жидкости) подчиняется закону, установленному Ньютоном: F   dv dZ S , где  – динамическая
вязкость; dv dZ – градиент скорости, показывающий быстроту изменения скорости в направлении оси Z , перпендикулярном направлению движения слоев; S –
площадь, на которую действует сила F .
В соответствии со вторым законом Ньютона dK dt  F взаимодействие двух
слоев можно рассматривать как процесс, при котором от одного слоя к другому в
единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение для силы трения можно заменить эквивалентным выражением:
K    dv dZ  S ,
где K – импульс, передаваемый от слоя к слою в единицу времени в положительном направлении оси Z .
Знак минус указывает, что импульс переносится в направлении убывания
скорости (поэтому знаки K и dv dZ противоположны).
Молекулярно-кинетическая теория позволяет получить для динамической
вязкости выражение  
1
v  .
3
Сопоставляя выражения законов Фика, Фурье и Ньютона:
M i  D  d i dZ  S , q     dT dZ  S , K    dv dZ  S ,
видим, что закономерности всех явлений (переноса массы, переноса тепла,
переноса импульса) сходны между собой. Эти законы были установлены задолго
до того, как они были обоснованы и выведены из молекулярно-кинетической теории, позволившей установить, что внешнее сходство их математических выражений обусловлено общностью лежащих в основе явлений теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в
процессе их хаотического движения и столкновений друг с другом.
Рассмотренные законы Фика, Фурье и Ньютона не вскрывают молекулярнокинетического смысла коэффициентов  , D, . Выражения для коэффициентов переноса выводятся из кинетической теории, и связываются эти коэффициенты с
характеристиками теплового движения молекул v и  . Из этих формул вытекают простые зависимости между  , D и  :    D и  cV   1 .
Используя эти формулы, можно по найденным из опыта одним величинам
определить другие, например, зная плотность и коэффициент диффузии газа –
определить вязкость и т. д.
2.4.4. Длина свободного пробега молекул
Характеристики теплового движения молекул v и  , входящие в выражения для
коэффициентов переноса, нетрудно определить. Формула для вычисления v была выведена ранее. Выведем формулу для вычисления длины свободного пробега молекул  .
Под столкновением двух молекул понимают процесс взаимодействия между молекулами, в результате которого молекулы изменяют направление своего движения.
Силы притяжения, действующие между молекулами, при сближении молекул на доста117
точно малое расстояние сменяются силами отталкивания. Молекулы быстро тормозятся, их скорость обращается в нуль. В этот момент имеет место наибольшее сближение
молекул друг с другом. После остановки молекулы разлетаются в разные стороны.
Минимальное расстояние, на которое сближаются центры двух молекул при
столкновении, называется эффективным диаметром молекулы d . Величина
   d 2 называется эффективным сечением молекулы.
За секунду молекула проходит в среднем путь v . Если за секунду она претерпевает в среднем  столкновений, то средняя длина свободного пробега будет
равна   v  . Для подсчета числа столкновений сначала предположим, что двигается только одна молекула, остальные стоят на месте. Ударившись об одну из
неподвижных молекул, она будет лететь прямолинейно до тех пор, пока не столкнется с какой-либо другой неподвижной молекулой. Столкновение произойдет,
если центр неподвижной молекулы окажется от прямой, вдоль которой летит молекула, на расстоянии меньшем, чем эффективный диаметр d . После столкновения молекула опять изменит направление своего движения и будет двигаться
прямолинейно, пока на пути не встретится молекула, центр которой будет находиться в пределах цилиндра радиусом d .
За секунду молекула проходит путь v . Число столкновений с неподвижными молекулами за это время равно числу молекул, центры которых попадают
внутрь коленчатого цилиндра длины v и радиуса d (рис. 2.4.2).
Рис. 2.4.2
Объем этого цилиндра –  d 2 v . Умножив этот объем на концентрацию n,
получим среднее число столкновений за одну секунду:     d 2 v n . В действительности все молекулы движутся, и число соударений определяется средней скоростью молекул по отношению друг к другу, а не по отношению к стенкам сосуда. Относительная скорость двух молекул равна: vотн  v2  v1 . Возведем выражение
2
2
  v2  v1   v22  v12  2v1v2 . Здесь учтено, что v 2  v 2 . Среднее значение
в квадрат: vотн
суммы равно сумме средних значений складываемых величин:
2
vотн
 v22  v12  2 v1v2 .
Значения скоростей первой и второй молекул v1 и v2 принимаются независимо друг от друга. Поэтому 2 v1v2  2 v1 v2 . Для газа, находящегося в равнове-
118
2
сии, v1  0, v2  0 . Значит, vотн
 v22  v12  2 v 2 , так как среднее значение квадрата скорости всех молекул одинаково.
Полученный результат означает, что относительное значение среднеквадратичной скорости молекул равно среднеквадратичному значению, умноженному на
корень квадратный из двойки: vотн ср.кв.  2 v ср.кв. . Средние квадратичные скоро-
сти пропорциональны средним арифметическим. Следовательно, vотн  2 v .
Заменив в выражении числа соударений     d 2 v n среднее значение скорости на
среднее относительное, т. е. 2 v , получаем для среднего числа столкновений за
секунду выражение:   2 d 2 v n и, подставив это значение в выражение для
длины свободного пробега   v  , будем иметь:

1
.
2 d 2 n
Заменив  d 2 через  , получим:   1


2 n . Поскольку n  р
 p  nkT  , то  
1 p (длина свободного пробега обратно пропорциональна давлению).
Эффективный диаметр молекулы уменьшается с повышением температуры. Значит, при повышении температуры длина свободного пробега увеличивается.
Оценим величину  и среднее число столкновений в секунду. Примем эффективный диаметр молекулы равным d  2 1010 м (два ангстрема). При нормальных условиях
моль газа занимает объем 22, 4 103 м3 . Отсюда   1  2  3,14  4 1020  3 1025   2 107 м .
Число столкновений в секунду можно получить, разделив среднюю скорость
молекул v на  . Скорость молекул равна  500v c . Отсюда  
500
 2,5 109 c 1 .
2 107
При нормальных условиях число столкновений молекул составляет несколько
миллиардов в секунду. С уменьшением давления число столкновений уменьшается.
Пример 1. Найти среднюю длину свободного пробега молекул азота при
температуре 17 С и давлении 10 4 Па .
Решение. Длина свободного пробега молекул газа равна  
1
. Здесь d –
2 d 2 n
эффективный диметр молекул, n – концентрация. По уравнению Клапейрона –
Менделеева, n  p  kT  . Диаметр молекул азота d  3 1010 м (приложение). Подставив данные задачи в выражение для длины свободного пробега, получим:

kT
1,38 1023  290

 106 м
2
20
4
2 d p
2  3,14  9 10 10
Пример 2. Во сколько раз уменьшится число столкновений в 1 с молекул
двухатомного газа, если объем газа адиабатически увеличить в 2 раза?
Решение. Число столкновений молекул равно   2 d 2 v n . Здесь d – эффек8RT
– среднеарифметическая скоM
8RT

n T
n . Значит, 1  1 1 .
рость молекул, M – молярная масса. Отсюда   2 d 2
M
 2 n2 T2
тивный диметр молекул, n – концентрация, v 
119
p1 V2

 2 . Для двухатомного газа
p2 V1
T
pn
  CP CV  1, 4 . По уравнению Клапейрона–Менделеева, 1  1 2  2 1 , поскольку
T2 p2 n1
При адиабатическом процессе pV   const 
концентрация при двукратном увеличении объема уменьшается в два раза. Следовательно,
1
 2 2 1  2,3 .
2
Пример 3. Чему равны при нормальных условиях коэффициенты диффузии
и внутреннего трения азота, если эффективный диаметр молекулы азота
d  3,11010 м ?
 5Па
; М 0,028 кг моль . Средняя арифметичеРешение. Т  273,15 К; р 1,013 10
8RT
 457 м с . Средняя длина свободного пробега молекул
M
кТ
рМ

 8, 72 108 м . Плотность  
 1, 25 кг м3 . Коэффициент внутреннего тре2
RT
2 в р
1
1
ния   v   16, 6 106 Н  с м 2 . Коэффициент диффузии D  v   1358 108 м 2 с .
3
3
ская скорость молекул v 
Пример 4. Какой толщины следовало бы сделать деревянную стену здания, чтобы она давала такую же потерю тепла, как кирпичная стена толщиной d  40 см при
одинаковой температуре внутри и снаружи здания. Коэффициенты теплопроводности
кирпича и дерева равны соответственно: к  0,70 Вт  м  К  , д  0,175 Вт  м  К  .
Решение. Запишем уравнение теплового потока через стену для обоих материалов: q   k
dд 
t1  t2
t t
 S ; q   д 1 2  S . Отсюда толщина деревянной стены составит
dk
dд
qд
d к  0,1м .
qk
Пример 5. При определении вязкости жидкостей по методу Стокса расчеты
ведут в предположении, что скорость падения шарика в жидкости vm  const . В какой степени верно это предположение? Через какой промежуток времени скорость шарика станет равной v1  0,995vm , если плотность материала шарика
1  7800 кг м3 , его диаметр
d  2 мм , динамическая вязкость жидкости
  0, 4 Н  с м2 . В начальный момент времени скорость шарика v0  0 .
Решение. Из дифференциального уравнения движения шарика:
m
  
dv
 mg  V 2 g  6 rv  mg 1  2   6 rv
dt
 1 
получим выражение для максимальной скорости (при которой dv dt  0 ):
2
2 r g  1   2 
vm 
и времени, по истечении которого скорость шарика станет рав9

2r 2 1
1
ной некоторому значению v :  
.
ln
9 v
9
1 2
2r g  1   2 
120
Подставив выражение для vm в последнее равенство, убеждаемся, что скорость опускания шарика станет постоянной и равной vm при t   .
Скорость шарика станет равной v  0,995vm через время   0, 023 с .
121
3. Электричество и магнетизм
3.1. Электрическое поле
3.1.1. Электрический заряд
Некоторые из элементарных частиц, входящих в состав атомов любого вещества, обладают особым свойством – несут электрический заряд. Заряд всех
элементарных частиц (если он не равен нулю) одинаков по абсолютной величине.
Его называют элементарным зарядом и обозначают буквой е. Несмотря на огромное разнообразие веществ в природе, существует только два типа электрических
зарядов, условно названных положительными и отрицательными. Одноименные
заряды друг от друга отталкиваются, разноименные – притягиваются.
Электрические заряды органически входят в состав любого тела. Обычно зарядов обоих знаков в теле присутствует поровну, и суммарный электрический заряд тела в этом случае равен нулю. Однако тело окажется заряженным, если ему какимлибо образом сообщить избыток положительных или отрицательных зарядов. Наличие у тела электрического заряда проявляется в том, что такое тело взаимодействует с
другими заряженными телами: отталкивается от них, либо притягивается.
Заряженное тело, размерами которого можно пренебречь по сравнению с
расстоянием от этого тела до других тел, несущих электрический заряд, называется точечным зарядом.
3.1.2. Закон Кулона
Закон, которому подчиняется сила взаимодействия точечных зарядов, был
установлен Кулоном. Этот закон гласит: «Сила взаимодействия двух точечных
зарядов пропорциональна величине каждого из взаимодействующих зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль
прямой, соединяющей заряды». В аналитической форме закон записывается следующим образом:
f K
q1q2
,
r2
или в векторном виде
f K
q1q2 r
.
r2 r
В векторном выражении под r следует понимать вектор, проведенный от
одного заряда к другому и имеющий направление к тому заряду, к которому приложена сила f . Поскольку каждый вектор можно записать как произведение его
модуля и единичного вектора, отношение r r есть единичный вектор, указывающий направление действия силы.
Коэффициент пропорциональности K выбором единиц измерения величин
f , q, r может быть сделан равным единице. В системе единиц СИ коэффициент
K отличен от единицы и равен 1 (4 0 ) , и закон Кулона принимает вид:
f 
q1q2
.
4 0 r 2
1
122
В системе СИ единицей заряда служит 1 кулон ( Kл ). Это очень большой заряд. Два заряда, величиной 1 Кл каждый, находящиеся на расстоянии 1 м друг от
друга, взаимодействуют с силой f  9 109 H . Элементарный заряд e , выраженный
в кулонах, равен e  1,6 1019 Кл .
Величина  0 называется электрической постоянной. Она относится к числу
фундаментальных физических констант и равна  0  8,85 1012 Кл 2  Н  м 2  .
Пример 1. Два положительных заряда q1 и q2 находятся на расстоянии r
друг от друга. Определить местоположение, величину и знак заряда q3 , чтобы все
заряды находились в равновесии.
Решение. Поскольку одноименные заряды отталкиваются, а разноименные
притягиваются, третий заряд может быть только отрицательным. Для того чтобы
система из трех зарядов находилась в равновесии, силы, действующие на каждый
заряд со стороны двух других зарядов, должны уравновешивать друг друга. Это
значит, что все три заряда находятся на одной прямой (рис. 3.1.1).
Рис. 3.1.1
По закону Кулона:
q1q2
4 0  r1  r2 
2

q1q3
qq
q
q
q1q3
q
q2
 2 3 2  21  22 .

 23 и
2
2
2
4 0 r1
4 0 r2
r1
r2
4 0 r1
 r1  r2  r1
Учитывая, что r2  r  r1 , находим: r1 
нение, получаем: q3 
r
. Подставляя r1 в первое урав1  q2 q1
q2
.
[1  q2 q1 ]2
3.1.3. Напряженность электрического поля
Взаимодействие между зарядами осуществляется через электрическое поле.
Всякий заряд изменяет свойства окружающего его пространства – создает в нем
электрическое поле. Это поле проявляет себя в том, что помещенный в какуюлибо его точку электрический заряд оказывается под действием силы. Это обстоятельство и используется для обнаружения и исследования электрического поля: в
данную точку пространства помещают некоторый «пробный» заряд. Для того
чтобы сила, действующая на пробный заряд, характеризовала поле в данной точке, пробный заряд должен быть точечным. В противном случае сила будет усреднена по объему, занимаемому телом.
123
Помещая в электрическое поле заряда q различные пробные заряды
3
и т. д., мы будем получать различные силы, действующие на пробный
q , q , qпр
1
пр
2
пр
заряд в данной точке поля: f 
1 qqпр
.
4 0 r 2
Однако отношение f qпр будет для всех пробных зарядов одинаково. Поэтому удобно принять это отношение в качестве характеристики электрического
поля: Е  f qпр .
Эту величину называют напряженностью электрического поля в данной точке.
Напряженность поля – векторная величина. Направление вектора Е совпадает с
направлением силы, действующей на положительный пробный заряд. Как следует из
выражения для силы Кулона, напряженность поля точечного заряда q равна:
E
1
q
.
4 0 r 2
В векторной форме равенство выглядит следующим образом:
E
1
q r
.
4 0 r 2 r
Направлен вектор напряженности поля точечного заряда вдоль радиальной
прямой, проходящий через заряд, создающий поле, и данную точку: от заряда, если он положительный, и к заряду, если он отрицательный.
За единицу напряженности электрического поля принимается напряженность в
такой точке, в которой на заряд, равный единице 1 Кл  , действует сила, величина которой также равна единице 1 Н  . Эта единица называется вольт на метр  В м  .
Если заряд qпр положительный, направление действующей на него силы
совпадает с направлением вектора напряженности Е ; если qпр отрицателен,
направления f и E противоположны.
Пример 2. Медный шар диаметром 1 см помещен в масло. Плотность масла
  800 кг м3 . Чему равен заряд шара, если в однородном электрическом поле шар
оказался взвешенным в масле? Электрическое поле направлено вертикально вверх
и его напряженность Е  3600 В см .
Решение. На шар действуют три силы: сила электрического поля F1 , направленная вверх, сила тяжести P , направленная вниз, и сила Архимеда F2 , направленная вверх. В равновесии P  F1  F2 , причем P  mg  1  4 3  r 3 g , где 1 – плотность меди; F1  Eq и F2  2  4 3  r 3 g , где  2 – плотность масла. Из выражений
для сил имеем: q 
4 r 3 g  1   2 
 1,1108 Кл .
3E
124
3.1.4. Принцип суперпозиции
Пусть электрическое поле создается некоторой системой зарядов. Как показывает опыт, сила, с которой действует такое поле на заряд, не входящий в систему, равна векторной сумме сил, с которыми действуют на данный заряд каждый
из зарядов системы в отдельности.
Значит, напряженность поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов системы в отдельности:
 Е  Е1  Е2  Е3  .....   Ei .
i
Это утверждение называется принципом суперпозиции электрических полей. Оно позволяет вычислить напряженность поля любой системы зарядов.
Пример 3. Точечные заряды q1  20 нКл и q2  10 нКл находятся в воздухе на
расстоянии r  10 см друг от друга. Определить напряженность поля Е в точке,
удаленной на расстояние r1  8 см от первого и r2  7 см от второго зарядов.
Решение. Напряженность поля, создаваемого в указанной точке первым зарядом, направлена от заряда и равна E1  q1  4 0 r12  (рис. 3.1.2). Напряженность поля,
создаваемого в этой точке вторым зарядом, направлена к заряду и равна
E2  q2  4 0 r22  .
Рис. 3.1.2
Величина суммарной напряженности и ее направление определяются диагональю параллелограмма, построенного на векторах Е1 и Е2 как на сторонах.
Сторона треугольника
r
по теореме косинусов равна r  r12  r22  2r1r2Cos ,
где  – угол между сторонами r1 и r2 . Отсюда Cos 
r12  r22  r 2
. Применяя теорему
2r1r2
косинусов к половине параллелограмма, находим: E12  E22  2 E1E2Cos  E 2 , где E –
суммарная напряженность. Отсюда
2
2
 q1   q2 
q1q2
r12  r22  r 2


2
 E2 ,


2 
2 
2 2 2
4

r
4

r
2
r
r
 4 0  r1 r2
0 1 
0 2 
1 2


т. е.
E
1
4 0


2
2
2
q12 q22 q1q2 r1  r2  r
 
.
r14 r24
r13r23
Подставив данные задачи, получим: Е  35 103 В м .
125
Пример 4. Найти напряженность электрического поля на продолжении оси
диполя и перпендикуляре к середине его оси (рис. 3.1.3).
Рис. 3.1.3
Решение. Электрический диполь – система двух равных по модулю разноименных точечных зарядов, расстояние между которыми значительно меньше
расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя
(прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя. Вектор
p  q  L , где q – величина зарядов диполя, L – плечо диполя, называется электрическим моментом диполя или дипольным моментом.
Согласно принципу суперпозиции, напряженность поля Е диполя в произвольной точке: E  E  E , где Е иE– – напряженности полей, создаваемых, соответственно, положительным и отрицательным зарядами.
На продолжении оси в точке А суммарная напряженность будет направлена
от диполя вдоль его оси. (Напряженность Е направлена к отрицательному заряду; напряженность Е направлена от положительного заряда. По модулю Е  Е ,
т. к. расстояние от точки А до положительного заряда меньше, чем до отрицательного заряда.) Модуль напряженности в точке А равен Е А  Е  Е . Обозначив расстояние от точки А до середины оси диполя через r , для напряженности в
точке А имеем
2
2

1 
q
q
q  r  L 2   r  L 2
EA 

.


4 0   r  L 2 2  r  L 2 2  4 0  r  L 2 2  r  L 2 2
Для диполя r  L , поэтому
EA 
1 2qL
1 2p
.

3
4 0 r
4 0 r 3
126
Напряженность поля на перпендикуляре, восстановленном к оси диполя из
его середины, можно определить следующим образом. Точка B равноудалена от
зарядов, поэтому модули напряженностей Е и Е равны между собой:
1
q
1 q
,
E  E 

2
2
4 0 r   L 4 4 0 r2
где r – расстояние от точки B до середины плеча диполя  r  L  .
Из подобия равнобедренных треугольников, опирающихся на плечо диполя
E
L
L
и вектор EB , получим B 
 , т.к.  r   L  . Отсюда
2
E
 L 2   r 2 r 
EB 
E L
1 qL
1 p
.


3
r
4 0 r 
4 0 r 3
Вектор Е имеет направление, противоположное электрическому моменту диполя.
3.1.5. Линии напряженности
Электрическое поле можно задать, указав для каждой точки величину и
направление вектора напряженности. Совокупность этих векторов образует поле
вектора напряженности электрического поля. Аналогично тому, как поле вектора
скорости можно наглядно представить с помощью линий тока, электрическое поле можно описать с помощью линий напряженности. Линии напряженности проводятся таким образом, чтобы касательная к ним в каждой точке совпадала с
направлением вектора Е . Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям площадки, было равно численному значению вектора Е . Тогда по картине линий
напряженности можно судить о направлении и величине вектора Е в разных точках пространства. Так как в каждой точке пространства вектор напряженности
имеет лишь одно направление, то линии напряженности никогда не пересекаются.
Для однородного поля, в котором вектор напряженности во всех точках постоянен по величине и направлению (например, поля между двумя разноименно
заряженными бесконечными пластинами), линии напряженности параллельны
вектору напряженности. Если поле создается точечным зарядом, то линии напряженности при положительном заряде – радиальные прямые, выходящие из заряда,
при отрицптельном заряде – входящие в него (рис. 3.1.4). Графический способ
представления электрического поля широко применяется в электротехнике.
Рис. 3.1.4
127
Линии напряженности нигде, кроме заряда, не начинаются и не заканчиваются; они, начавшись на заряде, уходят в бесконечность, если заряд положительный, либо, приходя из бесконечности, заканчиваются на заряде, если он отрицательный. Это свойство линий напряженности является общим для всех электрических полей, т. е. полей, создаваемых любой системой неподвижных электрических зарядов. Это становится понятным, если учесть, что полное число N линий
напряженности, пересекающих сферическую поверхность произвольного радиуса
r , окружающую заряд, будет равно произведению густоты линий на площадь поверхности сферы 4 r 2 . Густота линий по определению численно равна напря1 q
1 q
q
женности E 
. Следовательно, N 
4 r 2  , т. е. число линий на
2
2
4 0 r
4 0 r
0
любом расстоянии от заряда будет одно и то же. (Приведенное выражение для N
характеризует только численное равенство и не имеет физического смысла.)
3.1.6. Поток вектора. Теорема Гаусса
Введем понятие потока вектора через поверхность. Если имеется поле некоторого вектора А , то выражение Ф   An dS , где An  АCos – составляющая вектора
S
А по направлению нормали n к площадке dS , называется потоком вектора А через
поверхность S . Здесь  – угол между векторами А и n . Если величину dS рассматривать как вектор с модулем, равным dS , направленный по нормали n , то
можно написать: Ф   AdS , где AdS – скалярное произведение векторов А и dS .
S
В соответствии с этим определением выражение Ф   EdS есть поток векS
тора напряженности через поверхность S . Подынтегральное выражение есть ничто иное, как произведение напряженности на площадку, нормальную линиям
напряженности: EdS  ECos dS  EdS , т. е. численно равно количеству линий
напряженности, пронизывающих площадку dS . Значит, поток вектора напряженности численно равен количеству линий E , пронизывающих всю поверхность S .
Как было показано выше, поток вектора E сквозь охватывающую точечный заряд
сферическую поверхность оказывается равным q  0 . Нетрудно показать, что это
справедливо и для любой замкнутой поверхности, охватывающей заряд.
Пусть внутри замкнутой поверхности заключено несколько точечных зарядов произвольных знаков: q1 , q2 и т. д. Поток вектора E по определению равен:
Ф
 En dS
(интегрирование производится по замкнутой поверхности). В силу
S
принципа суперпозиции полей En  En1  En 2  ....   Eni .
i
128
Используя это, получаем:


 EndS    i Eni  dS  i  Eni dS , где
S
S
Eni – нор-
S
мальная составляющая напряженности поля, создаваемого i -м зарядом в отдельности. Но  Eni dS  qi  0 . Следовательно,
S


 EndS   i qi 
0 .
S
Доказанное равенство носит название теоремы Гаусса: «Поток вектора
напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на
электрическую постоянную».
3.1.7. Применение теоремы Гаусса для расчета электрических полей
Теорема Гаусса позволяет легко определить напряженность поля. Рассмотрим несколько случаев.
Поле бесконечной однородно заряженной плоскости. Поскольку плоскость
бесконечна и заряжена однородно (т. е. с постоянной плотностью), нет никаких
оснований к тому, чтобы сила, действующая на пробный заряд, отклонялась в какую-либо сторону от нормали к плоскости. Значит, напряженность в любой точке
поля имеет направление, перпендикулярное к плоскости.
Очевидно, что в симметричных относительно плоскости точках напряженность поля будет одинакова по величине и противоположна по направлению.
Мысленно вырежем цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величины S , расположенными относительно плоскости симметрично (рис. 3.1.5). Применим к этой поверхности теорему Гаусса. Поток вектора напряженности через боковую часть поверхности равен нулю, т. к. нормальная составляющая вектора напряженности в каждой ее
точке равна нулю En  0 . Для оснований E n совпадает с Е . Следовательно, суммарный поток вектора напряженности через поверхность 2ES . Внутри поверхq
) ).
ности заключен заряд S (  – поверхностная плотность заряда (  im
S 0 S
По теореме Гаусса, 2E S  S  0 , откуда E    2 0  .
Рис. 3.1.5
129
Поле двух разноименно заряженных плоскостей. Поле двух параллельных
бесконечных плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью  , можно найти как суперпозицию полей,
создаваемых каждой из плоскостей в отдельности. Очевидно, что в области между
плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна: Е    0 (рис. 3.1.6). Вне объема, ограниченного
плоскостями, складываемые поля имеют противоположные направления, так что
результирующая напряженность равна нулю.
Рис. 3.1.6
Поле бесконечного заряженного цилиндра. Рассмотрим поле, создаваемое
бесконечной цилиндрической поверхностью радиуса R , заряженной с постоянной
поверхностной плотностью  . Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой,
перпендикулярной к оси цилиндра, а модуль вектора напряженности может зависеть лишь от расстояния r от оси цилиндра.
Представим себе мысленно коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиусом r и высотой h (рис. 3.1.7). Для
оснований этого цилиндра En  0 , для боковой поверхности En  E  r  (заряд будем считать положительным). Поток вектора напряженности сквозь выделенную
замкнутую поверхность будет равен E  r   2 rh . Если r  R , внутрь поверхности
q 

попадает заряд q   h , где  – линейная плотность заряда    im
 . По теоL 0 L 

1 
реме Гаусса, E  r   2 rh   h  0 . Отсюда E  r  
для  r  R  . Если r  R ,
2 0 r
замкнутая поверхность не содержит внутри себя зарядов, вследствие чего
E  r   0 . Таким образом, внутри заряженной цилиндрической поверхности бесконечной длины поле отсутствует.
Рис. 3.1.7
130
Так как   2 R (это заряд на единицу длины), напряженность в непосредственной близости от поверхности  r  R  равна E  R     0 .
Поле заряженной сферической поверхности. Поле, создаваемое сферической поверхностью радиусом R , заряженной с постоянной поверхностной плотностью  , характеризуется центральной симметрией. Это значит, что направление вектора напряженности в любой точке проходит через центр сферы, а модуль
напряженности является функцией расстояния r от центра сферы. Для всех сферических поверхностей радиусом r  R имеем: En  E  r  и, следовательно,
E  r   2 r 2  q  0 , т. к. внутрь поверхности попадает весь заряд q , создающий
1 q
поле. Отсюда E  r  
. Если r  R , то внутри замкнутой поверхности не
4 0 r 2
будет зарядов, вследствие чего E  r   0 . Значит, внутри сферической поверхности, заряженной с постоянной поверхностной плотностью, поле отсутствует. Вне
этой поверхности поле имеет такой же вид, как поле точечного заряда той же величины, помещенного в центр сферы.
При r  R , учитывая, что q  4 R 2 , имеем для напряженности поля вблизи
заряженной сферической поверхности: E  R     0 .
Поле объемно заряженной сферы. Если сфера заряжена объемно с постоянной объемной плотностью  , то электрическое поле такой сферы также обладает
центральной симметрией. Вне сферы поле описывается так же, как и в случае поверхностно заряженной сферы. Однако для точек внутри сферы поле будет иным.
Сферическая поверхность радиусом r  R будет содержать внутри себя заряд
q
4
1 4
 r 3 . По теореме Гаусса, E  r   4 r 2 
,
 r 3 . Учитывая, что  
3
0 3
 4 3  R 3
1 qr
получаем: E  r  
. Внутри сферы напряженность поля растет линейно с
4 0 R3
расстоянием r от центра сферы, вне сферы напряженность поля убывает по такому же закону, как и у поля точечного заряда.
Пример 5. Два бесконечно длинных параллельных провода, расположенных в вакууме, заряжены равномерно с линейной плотностью заряда
  5 108 Кл м . Расстояние меду проводами R  0,5 м . Определить силу, действующую на единицу длины провода.
Решение. Определим напряженность электрического поля, создаваемого одним из проводов в том месте, где находится второй провод. Для этого построим
цилиндрическую поверхность, ось которой совпадает с проводом, радиус основания которого R и высота l . Из соображений симметрии следует, что вектор
напряженности в каждой точке перпендикулярен этой поверхности. Поток вектора напряженности через эту поверхность будет равен: Ф  Е  2 Rl .
С другой стороны, в соответствии с теоремой Гаусса, этот поток равен заряду,
заключенному внутри этой поверхности, деленному на  0 : Е  2 Rl  l   0 . Отсюда E    2 R 0  .
131
Сила,
F  E  l   
действующая
на
длину
l
второго
проводника,
равна

l . Сила, действующая на единицу длины проводника,
2 R 0
2
F
2
. Подставляя данные задачи, получаем: f  9 105 Н м .
f 

l 2 R 0
3.1.8. Работа сил электрического поля
Как мы уже убедились, напряженность – это силовая характеристика электрического поля. Вычислим работу, которая совершается силами поля неподвижного точечного заряда q над перемещающимся в этом поле точечным зарядом q  .
Работа на элементарном пути dL равна (рис. 3.1.8):
Рис. 3.1.8
dA  fdL  fdLCos 
1 qq
1 qq
dLCos


dr .
4 0 r 2
4 0 r 2
Полная работа на пути 1–2 равна:
r
qq 2 dr
1  qq qq 
A12 



.
4 0 r1 r 2 4 0  r1
r2 
Из последнего выражения видно, что работа сил поля не зависит от пути, по
которому перемещался в этом поле заряд q  , а определяется лишь начальным и
конечным положением этого заряда. Следовательно, силы, действующие на заряд
в поле, создаваемом неподвижными зарядами, являются потенциальными. Работа
потенциальных сил на замкнутом пути, как известно из механики, равна нулю.
Выражение для работы по перемещению заряда на участке 1–2 можно записать
следующим образом:
r2
r2
r2
r1
r1
r1
A12   fdr  q  Edr  q  Edr  q EdLCos  q ELdL ,
132
L
L
где E L – проекция вектора напряженности на направление элементарного
перемещения dL . (Здесь учтено, что угол между векторами E и dr равен нулю).
Поскольку q  const  0 , то на замкнутом пути  EL dL  0 .
L
Интеграл по замкнутому контуру вида
 EL dL называется циркуляцией векL
тора E по данному контуру. Таким образом, циркуляция вектора напряженности
по любому замкнутому контуру равна нулю.
Пример 6. Какая совершается работа при перенесении точечного заряда в
8
2  10 Кл из бесконечности в точку, находящуюся на расстоянии 1 см от поверхности шара радиусом 1 см с поверхностной плотностью заряда   109 Кл см2 ?
Решение. Поверхность шара S  4 R 2 . Значит, заряд на шаре равен
q   S  4 R 2 . Работа по перемещению заряда из бесконечности в данную точку поля будет равна:
qq  1 1  4 R 2 q 
1
1  0,012 105  2 108
А
 
 1,13  104 ( Дж).
  

12
4 0  r  
4 0  R  0,01   8,85 10  0,02
3.1.9. Потенциал
Поскольку электростатическое поле потенциально, любой заряд, помещенный в такое поле, обладает потенциальной энергией, за счет которой силами поля
совершается работа. Значит, работа по перемещению заряда в электростатическом
поле может быть представлена как разность значений потенциальной энергии этого заряда в начальном и конечном положениях:
1 qq
1 qq
A12 

 W1  W2 .
4 0 r1 4 0 r2
1 qq
 const .
4 0 r
Значение константы можно найти из условия, что на бесконечности W  r     0 . При
1 qq
этом условии W 
.
4 0 r
 , qпр
 , qпр
 и т. д. будут обладать в одной и той же
Разные пробные заряды qпр
точке различной энергией W ,W ,W  и т. д. Но, как видно из выражения для потенциальной энергии, отношение энергии к пробному заряду от величины пробного заряда не зависит. Величина этого отношения называется потенциалом поля
в данной точке и обозначается   W
. Потенциал наряду с напряженностью
qпр
используется для описания полей. Используя выражение для потенциальной энер1 q
гии, потенциал можно записать в следующем виде:  
.
4 0 r
Значит, выражение для потенциальной энергии имеет вид: W 
133
Нетрудно показать, что потенциал поля, создаваемого системой зарядов, равен
алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности:
1
qi
.


4 0
ri
Поскольку W  q   , то работа по переносу заряда q в электростатическом поле может быть выражена через разность потенциалов: A12  W1  W2  q 1  2  . Если
заряд переносится из данной точки поля на бесконечность, где   0 , то A  q .
В системе СИ за единицу потенциала, называемую вольтом, принимается
потенциал в такой точке, для перемещения в которую из бесконечности заряда,
1 Дж
равного 1 Кл , нужно совершить работу в 1 Дж : 1 В 
.
1 Кл
Поскольку электрическое поле можно описать либо с помощью вектора
напряженности, либо с помощью скаляра потенциала, то между этими величинами
должна существовать определенная связь. Действительно, работа поля над зарядом q на отрезке пути dl может быть представлена, с одной стороны, как qEl dl , а с
другой стороны, как убыль потенциальной энергии d  q  , т. е. d  q   qEl dl .


dl  El  
Отсюда qEl dl  q
. В качестве l взято произвольное направлеl
l
ние. Используя декартову систему координат, можно записать:



Ex   , E y   , Ez  
 E  iEx  jE y  kEz 
x
y
z
 

 
  i
j
k
  grad .
y
z 
 x
Эта формула позволяет по известным значениям потенциала найти напряженность поля в каждой точке. Можно решить и обратную задачу: по заданным в
каждой точке значениям напряженности найти разность потенциалов между двумя произвольными точками. Действительно, работа, совершаемая силами поля
над зарядом q при перемещении его из точки 1 в точку 2, может быть вычислена
2
как
A12   qEl dl . Но эта же работа может быть представлена в виде:
1
2
A12  q 1  2  . Значит, 1  2   El dl . Интеграл берется по любой линии, соеди1
няющей точки 1 и 2.
Для наглядного изображения поля можно вместо линий напряженности
воспользоваться эквипотенциальными поверхностями или поверхностями равного
потенциала. Эквипотенциальная поверхность – это такая поверхность, все точки
которой имеют одинаковый потенциал. Нетрудно показать, что линии напряженности в каждой точке ортогональны эквипотенциальным поверхностям. Чтобы
убедиться в этом, проведем в некоторой точке касательную  к эквипотенциаль134
ной поверхности (рис. 3.1.9). При смещении вдоль  на бесконечно малую вели

 0 . Но
чину d потенциал  не изменится, так что
с точностью до знака


равно проекции вектора напряженности E на направление  . Следовательно,
тангенциальная составляющая вектора E равна нулю, откуда вытекает, что вектор E направлен по нормали к поверхности, а поскольку направление E - это
направление касательной к линии E , то линии E в каждой точке ортогональны
эквипотенциальным поверхностям.
Рис. 3.1.9
Эквипотенциальную поверхность можно провести через любую точку поля.
При графическом изображении поля принято проводить поверхности так, чтобы
разность потенциалов для двух соседних поверхностей была везде одна и та же.
Тогда по густоте эквипотенциальных поверхностей можно судить о величине
напряженности поля: чем гуще располагаются поверхности, тем больше в данном
месте grad , а значит и E .
Пример 7. Шарик массой 1 г и зарядом 108 Кл перемещается из точки А ,
потенциал которой 600 В , в точку В , потенциал которой равен нулю. Чему была
равна его скорость в точке А , если в точке В она стала равной 20 см с ?
Решение. Работа по перемещению заряда q  108 Кл из точки с потенциалом
1  600 В в точку с потенциалом, равным нулю, равна:
А  (2  1 )  q  600  108  0,6  105 ( Дж) .
Кинетическая энергия шарика в конце пути равна:
mv22 103  0,04
W2 

 2  105  Дж  .
2
2
Вся работа пошла на увеличение кинетической энергии. Значит, в точке А
кинетическая энергия шарика была равна:
mv12
W1 
 2  105  0,6  105  1,4  105  Дж  .
2
2,8  105
 16,7  102  м с  .
Отсюда v1 
3
10
Пример 8. Известно, что градиент потенциала электрического поля Земли у
ее поверхности направлен вертикально вниз и равен (в среднем) 130 В м . Найти
среднюю поверхностную плотность заряда Земли.
135
Решение. Градиент потенциала с точностью до знака равен напряженности
электрического поля, т. е. Е  130 В м . С другой стороны, напряженность поля
поверхностно заряженного шара равна Е    0 , где  – поверхностная плотность заряда. Отсюда
  Е 0  130  8,85 1012  1,15 109 ( Кл м2 ) .
3.2. Диэлектрики и проводники в электрическом поле
Введем понятия диэлектрика, проводника и полупроводника. Если заряженные частицы, например, электроны, могут более или менее свободно перемещаться, то соответствующее вещество способно проводить электрический ток. Носителями заряда, движение которых создает электрический ток, могут быть не только электроны, но и ионы, т. е. атомы или молекулы, потерявшие либо присоединившие к себе один или несколько электронов.
В соответствии со способностью проводить электрический ток все вещества
подразделяются на диэлектрики (или изоляторы), проводники и полупроводники.
Идеальных изоляторов в природе не существует. Все вещества хотя бы в ничтожной степени проводят электрический ток. Однако вещества, называемые диэлектриками, проводят ток в 1015  1020 раз хуже, чем вещества, называемые проводниками. Полупроводниками называется обширная группа веществ, которые по
способности проводить ток заполняют промежуточную область между проводниками и диэлектриками.
3.2.1. Диэлектрики
Диэлектрик, как и всякое вещество, состоит из атомов и молекул. Так как
положительный заряд всех ядер молекулы равен суммарному заряду электронов,
молекула в целом электрически нейтральна. Если диэлектрик внести в электрическое поле, то и поле, и сам диэлектрик претерпевают существенные изменения.
Чтобы понять это, нужно учесть, что электроны движутся в пределах атома или
молекулы с огромной скоростью, непрерывно меняя свое положение относительно ядер. Поэтому действие каждого электрона на внешние заряды будет примерно
таким же, как если бы он находился в покое в некоторой точке.
Для расстояний, больших по сравнению с размерами молекулы, действие
электронов эквивалентно действию их суммарного заряда, помещенного в некоторую точку внутри молекулы. Назовем эту точку центром тяжести отрицательных зарядов. Аналогично действие ядер эквивалентно действию их суммарного
заряда, помещенного в центр тяжести положительных зарядов.
Если заменить положительные заряды ядер молекул суммарным зарядом
 q , находящимся в центре тяжести положительных зарядов, а заряд всех электронов – суммарным отрицательным зарядом q , находящимся в центре тяжести
отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом p  q L .
136
Диэлектрические вещества, молекулы которых имеют симметричное строение (например, N 2 , H 2 , O2 , CO2 , CH 4 и др.), т. е. центры тяжести положительных и
отрицательных зарядов в отсутствие внешнего электрического поля совпадают и,
следовательно, дипольный момент молекулы равен нулю, образуют первую группу диэлектриков. Молекулы таких диэлектриков называются неполярными. Под
действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные заряды – по полю, отрицательные – против поля), и молекула приобретает дипольный момент.
Вторую группу диэлектриков ( H 2O, NH 3 , SO2 , CO и др.) составляют вещества,
молекулы которых имеют асимметричное строение, т. е. центры тяжести положительных и отрицательных зарядов в отсутствие электрического поля не совпадают.
Таким образом, эти молекулы и в отсутствие внешнего электрического поля обладают дипольным (собственным электрическим) моментом. Молекулы таких диэлектриков называются полярными. Однако в отсутствие внешнего электрического поля
дипольные моменты полярных молекул вследствие теплового движения ориентированы в пространстве хаотично, и их результирующий момент равен нулю.
Выделяют еще и третью группу диэлектриков ( NaCl , KCl , KBr и т. п.), которую составляют вещества, с молекулами, имеющими ионное строение. Ионные
кристаллы представляют собой пространственные решетки с правильным чередованием ионов разного знака. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему вдвинутых одна в другую ионных
подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению дипольных моментов.
Таким образом, внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика или, иными словами, к поляризации диэлектрика. Поляризацией диэлектрика называется процесс ориентации диполей или появления под
воздействием электрического поля ориентированных по полю диполей.
Процесс поляризации неполярной молекулы протекает так, как если бы положительные и отрицательные заряды молекулы были связаны друг с другом
упругими силами. Поэтому говорят, что неполярная молекула ведет себя во
внешнем электрическом поле как упругий диполь.
Действие внешнего поля на полярную молекулу сводится в основном к
стремлению повернуть молекулу так, чтобы ее электрический момент установился по направлению поля. На величину электрического момента внешнее поле
практически не влияет. Значит, полярная молекула ведет себя во внешнем поле
как жесткий диполь.
Поскольку молекулы по электрическим свойствам эквивалентны диполям,
для понимания явлений в диэлектриках необходимо знать, как ведет себя диполь
во внешнем электрическом поле.
137
3.2.2. Диполь в электрическом поле и диэлектрике
Заряды, образующие диполь, в однородном электрическом поле находятся
под действием равных по величине, но противоположных по направлению сил f1
и f 2 (рис. 3.2.1). Эти силы образуют пару, плечо которой равно LSin ( L – расстояние между зарядами;  – угол между направлением поля и осью диполя), т. е.
зависит от ориентации диполя относительно поля. Модуль каждой силы – qE .
Рис. 3.2.1
Отсюда для момента пары сил имеем: M  qELSin  рESin , где p – электрический момент диполя. Этот момент стремится повернуть диполь по полю.
Для того чтобы повернуть диполь против поля на угол d , необходимо совершить работу против сил, действующих на диполь: dA  Md  pESin d . Эта работа идет на увеличение потенциальной энергии W , которой обладает диполь в
электрическом поле: dW  pESin d . Интегрируя это выражение, получаем
W   pECos  const . Полагая const  0 , получаем окончательное выражение для
энергии: W   pECos   pE . При таком выборе константы энергия диполя равна нулю в том случае, когда диполь устанавливается перпендикулярно полю.
Наименьшее значение энергии, равное  pE , получается при ориентации диполя
по направлению поля; наибольшее, равное pE , – при моменте p , направленном в
сторону, противоположную E .
Итак, в отсутствие внешнего электрического поля дипольные моменты молекул диэлектрика или равны нулю (для неполярных молекул), или распределены по
направлениям в пространстве хаотическим образом (для полярных молекул). В обоих
случаях суммарный диэлектрический момент диэлектрика равен нулю. Под действием
внешнего поля диэлектрик поляризуется. Степень поляризации возрастает с увеличением напряженности поля и в значительной мере зависит от природы диэлектрика.
Пример 1. В стакан с керосином помещен металлический шарик, вблизи которого из трубки выходят небольшие пузырьки воздуха, поднимающиеся вертикально
вверх. Как будут двигаться пузырьки воздуха, если шарик зарядить электричеством?
Решение. Пузырьки воздуха будут отталкиваться от шарика, и траектория их изогнется (рис. 3.2.2). Это происходит оттого, что диэлектрическая проницаемость керосина больше, чем воздуха. Следовательно, на поверхности пузырька, обращенной к шарику, возникнут связанные заряды одного знака с зарядом шарика.
138
Рис. 3.2.2
Электрическое поле в диэлектрике
Допустим, в вакууме образовано электрическое поле с напряженностью Е0 ,
а затем в это поле внесен диэлектрик (рис. 3.2.3). В результате поляризации диэлектрика на его поверхностях образуются заряды противоположного знака, и в
нем возникает собственное электрическое поле с напряженностью Ес , направленное противоположно внешнему полю. Напряженность результирующего поля в
диэлектрике при этом уменьшается по сравнению с напряженностью Е0 поля в
вакууме и численно равна разности Е  Е0  Ес .
С другой стороны, напряженность Е результирующего поля в диэлектрике
может быть выражена как некоторая доля напряженности Е0 поля в вакууме:
1
Е  Е0 , где  – некоторая постоянная, характерная для данного диэлектрика.

Рис. 3.2.3
Постоянная  называется относительной диэлектрической проницаемостью
и показывает, во сколько раз напряженность поля, образуемого некоторыми зарядами в данном диэлектрике, меньше напряженности поля, образуемого этими же
Е
зарядами в вакууме   0 .
Е
Относительная диэлектрическая проницаемость зависит, главным образом,
от природы вещества, и величина ее обусловлена способностью молекул вещества
поляризоваться под действием электрического поля. Численно  составляет для
большинства веществ значения от нескольких единиц до нескольких десятков
единиц. Например, для воздуха   1,0 , для стекла   6  10 , для воды   81 .
139
Если в электрическое поле в вакууме внести точечный заряд, то на него будет действовать сила f  qE0 . Чтобы заряженное тело поместить в поле, созданное в диэлектрике, в этом диэлектрике нужно сделать полость. В жидком или газообразном диэлектрике такую полость образует само тело, вытесняя диэлектрик
из занимаемого им объема. На поверхности полости возникают связанные заряды,
поэтому поле внутри полости будет отлично от поля Е в сплошном диэлектрике.
Таким образом, силу, действующую на помещенное в диэлектрик заряженное тело, нельзя вычислять как произведение величины заряда на напряженность поля.
В общем случае вычисление этой силы – задача весьма сложная. Только в случае
безграничного жидкого или газообразного диэлектрика силу, действующую со
стороны поля на помещенный в него точечный заряд, можно определить как произведение величины заряда на напряженность поля в диэлектрике f  qE .
Напряженность поля, создаваемого в однородном безграничном диэлектрике тоЕ
1 q1
чечным зарядом, равна: Е  0 
, где q1 – заряд, создающий поле E ;  –
 4 0  r 2
диэлектрическая проницаемость диэлектрика. Отсюда для силы взаимодействия
двух точечных зарядов, погруженных в однородный безграничный диэлектрик,
1 q1q2
можно написать f 
. Закон Кулона в таком виде применим только для
4 0  r 2
жидких и газообразных диэлектриков.
Пример 2. Два точечных заряда, находясь в воздухе на расстоянии 20 см
друг от друга, взаимодействуют с некоторой силой. На каком расстоянии эти заряды нужно поместить в масле, чтобы получить ту же силу взаимодействия?
Решение. По закону Кулона сила взаимодействия двух точечных зарядов
1 q1q2
равна: F 
, где  – диэлектрическая проницаемость среды. Для возду4 0 r 2
1
1
ха   1, для масла –   5 (см. приложение). Следовательно, 2  2 , где r и r1 –
r
5r1
расстояния между зарядами в воздухе и в масле соответственно. Отсюда
r1  r 5  8,94(см) .
3.2.3. Сегнетоэлектрики. Пьезоэлектрический эффект
Существует группа веществ, которые могут обладать спонтанной (самопроизвольной) поляризацией в отсутствие внешнего поля. Это явление было открыто
первоначально для сегнетовой соли (двойная калиево-натриевая соль винной кислоты KNaC4 H 4O6  4 H 2O ). В связи с этим все подобные вещества получили название сегнетоэлектриков.
Сегнетоэлектрики отличаются от остальных диэлектриков некоторыми особенностями. В частности, они обладают очень высокой диэлектрической проницаемостью.
В кристаллах сегнетоэлектрика имеются области, в которых дипольные моменты частиц параллельны друг другу в пределах данной области. Такие области
140
называются доменами. В смежных доменах в отсутствие внешнего электрического поля направления дипольных моментов различны. При внесении сегнетоэлектрика в электрическое поле происходит переориентация дипольных моментов доменов по полю. Возникшее при этом суммарное электрическое поле доменов будет поддерживать ориентацию доменов и после прекращения действия внешнего
электрического поля. Возникает так называемая остаточная поляризация. По причине очень сильного суммарного электрического поля доменов сегнетоэлектрики
обладают аномально большими значениями диэлектрической постоянной (для сегнетовой соли   104 ).
Сегнетоэлектрические свойства сильно зависят от температуры. Для каждого сегнетоэлектрика имеется температура, выше которой его необычные свойства
исчезают, и он становится обычным диэлектриком. Это температура называется
точкой Кюри. Сегнетова соль имеет две точки Кюри (остальные сегнетоэлектрики
по одной): 18 С и 24 С . Ее свойства сохраняются лишь в указанном температурном интервале.
Важное практическое значение имеет сегнетоэлектрик титанат бария
BaTiO3 с точкой Кюри 125 C .
Некоторые кристаллы (в том числе все сегнетоэлектрики) при деформации
поляризуются. Это явление называется прямым пьезоэлектрическим эффектом.
Величина поляризации пропорциональна деформации, следовательно, механическому напряжению.
Пьезоэлектрический эффект имеет следующее объяснение. Решетку всякого
кристалла можно представить в виде нескольких образованных разными атомами
более простых решеток (подрешеток), вставленных друг в друга. Если кристалл
не имеет центра симметрии, то при деформации происходит сдвиг простых решеток друг относительно друга, который может вызвать у кристалла появление
электрического момента.
Практическая безынерционность пьезоэлектрического эффекта позволяет
использовать пьезоэлектрические кристаллы для изготовления различных датчиков (например, пьезодатчиков давления), используемых в измерении импульсных
величин.
Наряду с указанным прямым эффектом у пьезоэлектрических кристаллов
наблюдается и обратный эффект, заключающийся в том, что поляризация под
действием электрического поля сопровождается механическими деформациями
кристалла. Если на металлические обкладки пьезокерамической пластинки подать
переменное электрическое напряжение, то пластинка будет попеременно растягиваться и сжиматься, т. е. в ней возникнут механические колебания, которые станут особенно интенсивными, если частота переменного напряжения совпадет с
собственной частотой пластинки. Такие настроенные в резонанс пьезоэлектрические пластинки используются для возбуждения ультразвуковых волн.
141
3.2.4. Проводники в электрическом поле
При внесении незаряженного проводника в электрическое поле носители
заряда приходят в движение: положительные – в направлении вектора напряженности Е , отрицательные – в противоположную сторону. У концов проводника
будут накапливаться заряды противоположного знака, называемые индуцированными зарядами. Поле этих зарядов направлено противоположно внешнему полю,
поэтому накапливание зарядов у концов проводника будет приводить к ослаблению поля в нем. Это будет продолжаться до тех пор, пока не установится равновесное распределение зарядов, при котором электрическое поле внутри проводника обращается в нуль. В самом деле, если бы внутри проводника имелось поле,
то оно вызвало бы упорядоченное движение зарядов без затраты энергии от
внешнего источника, что противоречит закону сохранения энергии. Значит, внутри проводника напряженность поля равна нулю: Е  0 . Отсутствие поля внутри
проводника означает, что потенциал во всех точках внутри проводника постоянен. Отсюда следует, что поверхность проводника в электрическом поле является
эквипотенциальной. Значит, и напряженность поля на поверхности проводника
должна быть в каждой точке направлена по нормали к поверхности, т. к. линии
напряженности ортогональны эквипотенциальным поверхностям.
Так как поле внутри проводника отсутствует, проводник, внесенный в электрическое поле, разрывает часть линий напряженности – они заканчиваются на
отрицательных индуцированных зарядах и вновь начинаются на положительных.
Индуцированные заряды располагаются на поверхности проводника, поле
внутри проводника отсутствует, поэтому если в проводнике имеется полость, то и
в ней поле отсутствует. На этом основана электростатическая защита приборов от
воздействия внешних полей.
3.2.5. Электроемкость. Конденсаторы
Если проводнику, уже несущему заряд q , сообщить заряд той же величины,
то второй заряд должен распределиться по проводнику точно таким же образом,
как и первый; в противном случае он создаст в проводнике поле, не равное нулю.
Увеличение в некоторое число раз заряда приводит к увеличению в то же число
раз напряженности поля в каждой точке окружающего проводник пространства.
Следовательно, в такое же число раз возрастает работа переноса по любому пути
единичного заряда из бесконечности на поверхность проводника, т. е. потенциал
проводника. Значит, для уединенного проводника q  C . Коэффициент пропорциональности C между потенциалом и зарядом называется электроемкостью или
просто емкостью. Емкость уединенного шара радиусом R , погруженного в безграничный диэлектрик, с диэлектрической проницаемостью  равна: C  4 0 R .
2
Это легко доказать: так как 1  2   Еl dl , где l – произвольное направление.
1
Пусть точки 1 и 2 соответствуют бесконечности 1  0  и поверхности шара со142
1
q
ответственно. Для шара El  E 
, то
4 0  r 2
q
пользуя это, получим: С   4 0 R .
 
1
R
q
1
q
. Исdr 
4 0   r 2
4 0  R


За единицу емкости принимается емкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1 Кл . Эта единица емкости
называется фарадой. Емкостью в 1Ф обладал бы уединенный шар радиусом
R  9 106 км, т. е. примерно в 1500 раз большим чем радиус Земли.
На практике используются единицы, равные долям фарады: микрофарада (106 Ф )
и пикофарада (1012 Ф ).
Уединенные проводники обладают малой емкостью: даже шар размером с
Землю имеет емкость всего 700 мкф . На практике же требуются устройства, которые при небольшом относительно окружающих тел потенциале накапливали бы
на себе значительные по величине заряды. В основу таких устройств, называемых
конденсаторами, положен тот факт, что электроемкость проводника возрастает
при приближении к нему других тел. Действительно, под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле возникают индуцированные или связанные заряды. Заряды, противоположные по знаку заряду
проводника q , располагаются ближе к проводнику, чем одноименные с q , следовательно, они оказывают большее влияние на его потенциал (они ослабляют поле
заряда q ). Поэтому при поднесении к заряженному проводнику какого-либо тела
потенциал проводника уменьшается по абсолютной величине. Согласно зависимости q  C , при этом увеличивается емкость.
Конденсаторы делают в виде двух проводников, расположенных близко
друг к другу. Образующие конденсатор проводники называются его обкладками.
Чтобы внешние тела не оказывали воздействия на емкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы
поле, создаваемое накапливаемыми на них зарядами, было полностью сосредоточено внутри конденсатора. Этому условию удовлетворяют две пластины, расположенные близко друг к другу, два коаксиальных цилиндра и две концентрические сферы. Соответственно, бывают плоские, цилиндрические и сферические
конденсаторы.
Под емкостью конденсатора понимается физическая величина, пропорциональная заряду q и обратно пропорциональная разности потенциалов между обq
кладками: С 
.
1  2
Величина емкости определяется геометрией конденсатора (формой и размерами обкладок и величиной зазора между ними), а также диэлектрическими свойствами среды, заполняющей пространство между обкладками. Очень просто вычисляется емкость плоского конденсатора. Если площадь обкладки S , а заряд на
143

q
. Прене
 0  0 S
брегая концевыми эффектами у краев обкладок (т. е. считая обкладки достаточно
большими), можно принять, что поле между обкладками однородно: напряженность во всех точках одинакова по величине и направлению. Тогда
ней q , то напряженность поля между обкладками равна E 
d
qd
, где d – расстояние между пластинами. Отсюда для
 0 S
0
 S
емкости плоского конденсатора получается следующая зависимость: С  0 .
d
Несколько сложнее выглядят формулы для емкости цилиндрического и
сферического конденсаторов. Для напряженности поля бесконечного заряженного
1 
1 q
цилиндра мы получали выражение E  r  
, где  – диэлектри
2 0 r 2 0 lr
q
ческая проницаемость среды (см. п. 3.1.7). Здесь   – линейная плотность заl
рядов на цилиндре ( l – длина цилиндра). Разность потенциалов между обкладкаR2
R2
q
dr
q
R2
ми находим путем интегрирования: 1  2   E  r  dr 

ln
2 0 l R1 r 2 0 l R1
R1
1  2   El dl  Ed 
( R1 и R2 – радиусы внутренней и внешней обкладок). Разделив q на найденное
значение разности потенциалов, получим емкость цилиндрического конденсатора: C   2 0 l   n  R2 R1  .
Для сферического конденсатора напряженность поля между обкладками
1 q
равна: E  r  
(см. п. 3.1.7). Разность потенциалов находится путем инте4 0 r 2
грирования:
R2
R
q 2 dr
q 1
1 
q R2  R1
1  2   E  r  dr 

  
2

4 0 R1 r
4 0  R1 R2  4 0 R1R2
R1
( R1 и R2 – радиусы внутренней и внешней обкладок). Отсюда для емкости
получается выражение: С  4 0 R1R2  R2  R1  .
Из трех выражений для емкости конденсаторов ясно, что введение между
обкладками прослойки из сегнетоэлектрика позволяет получать при небольших
размерах конденсатора большую емкость.
На практике конденсаторы часто соединяют в батареи, значительно расширяя диапазон возможных значений емкости. Конденсаторы можно соединять параллельно (рис. 3.2.4), и тогда одна из обкладок каждого конденсатора будет
иметь потенциал 1 , а другая – 2 . Следовательно, суммарный заряд на каждой из
двух систем обкладок будет равен:
q   qi   Ci 1  2   1  2   Ci .
i
i
i
144
Емкость всей батареи получается путем деления суммарного заряда на приложенное к ней напряжение: С   Сi . Значит, при параллельном соединении
i
конденсаторов емкости складываются.
Конденсаторы можно соединить последовательно (рис. 3.2.5), и тогда каждая
вторая обкладка предыдущего конденсатора и каждая первая обкладка следующего
конденсатора образуют единый проводник, на котором при подаче напряжения на батарею возникают индуцированные заряды той же величины, как и на первой обкладке
первого и второй обкладке последнего конденсаторов. Следовательно, для всех конденсаторов, включенных последовательно, величина заряда на обкладках одинакова.
q
Отсюда напряжение на каждом из конденсаторов равно: U i  .
Ci
Рис. 3.2.4
Рис. 3.2.5
Сумма этих напряжений равна разности потенциалов, приложенной к батарее:
q
1
1  2  U i    q .
i
i Ci
i Ci
1
1
Значит,
  . При последовательном соединении конденсаторов склаC
i Ci
дываются величины, обратные их емкостям.
Энергия заряженного проводника
Любой заряд, находящийся в поле другого заряда, обладает потенциальной
энергией. Следовательно, потенциальной энергией обладает любая система зарядов. Найдем потенциальную энергию двух неподвижных точечных зарядов q1 и
q2 , находящихся на расстоянии r друг от друга. Значения энергий этих зарядов
равны: W1  q1 2 и W2  q21 , где 1 и 2 – потенциалы, создаваемые зарядом q1 в
точке расположения заряда q2 и зарядом q2 в точке расположения заряда q1 соот1
2
ветственно.
Потенциалы
и
определяются
зависимостями:
1
1 q1
1 q2
, поэтому W1  W2  W и W  q12  q21   q12  q21  .
1 
; 2 
4 0 r
4 0 r
2
Добавляя к системе из двух зарядов последовательно заряды q3 , q4 и т. д., легко
убедиться в том, что в случае n неподвижных зарядов энергия их взаимодействия
145
1 n
 qii , где  i – потенциал, создаваемый в той точке, где находится
2 i 1
заряд qi , всеми зарядами, кроме i -го.
Заряд q , находящийся на некотором проводнике, можно рассматривать как
систему точечных зарядов dq . Такая система обладает энергией, равной работе,
которую нужно совершить, чтобы перенести все заряды dq из бесконечности на
поверхность проводника. Перенос первой порции заряда не требует совершения
работы, так как потенциал проводника первоначально равен нулю. Перенос каждой следующей порции требует совершения работы, равной: dA   dq  q  dq ,
C
где  – потенциал проводника, обусловленный уже имеющимся на нем зарядом;
С – емкость проводника. Эта работа идет на увеличение потенциальной энергии
1
q2
проводника: dW  qdq . Отсюда W 
 const . Энергия незаряженного проC
2C
q 2 q C 2
водника равна нулю, значит const  0 и W 
.


2C 2
2
равна: W 
Энергия электрического поля
Аналогичным образом можно показать, что энергия заряженного конденсаq 2 qU CU 2
тора равна: W 
, где через U обозначена разность потенциалов


2C
2
2
между обкладками. Энергию конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Для плоского
конденсатора:
2
CU 2  0 SU 2  0  U 
W


  Sd .
2
2d
2 d
U
  E2
 E и Sd  V – объем поля, то W  0
V . Эта зависимость
Так как
2
d
связывает энергию конденсатора с напряженностью поля.
Используя выражения для энергии конденсатора, можно определить силу, с
которой обкладки плоского конденсатора притягивают друг друга. Пусть расстояние между обкладками изменилось на dx . Тогда сила притяжения совершила работу dA  Fdx . Эта работа сопровождается убылью потенциальной энергии:
q2
2
Fdx  dW . Отсюда F   dW dx . Поскольку W  q  2C  
x , то для силы
2 0 S
притяжения пластин конденсатора имеем: F   q 2  2 0 S  . Знак минус указывает, что сила F является силой притяжения.
146
Пример 3. С какой силой взаимодействуют пластинки плоского конденсатора площадью S  0,01 м2 , если разность потенциалов между ними U  500 В и
расстояние d  3 мм ?
Решение. Емкость конденсатора в общем случае – C  q U . Принимая во
внимание выражение для емкости плоского конденсатора C   0 S d , получаем:
q  CU   0 SU d . Отсюда для силы взаимодействия пластинок конденсатора
имеем:
F 
q2
2 0 S

 0 SU 2
2d 2
.
Подставляя
данные
задачи,
получаем:
F  12,3 104 H .
Пример 4. Металлический шарик радиусом r1 зарядили количеством электричества q . Затем его соединили с другим шариком радиусом r2 . Доказать, что
условие равенства их потенциалов эквивалентно условию минимума электрической энергии этой системы. Расстояние между шарами велико по сравнению с их
радиусами.
Решение. Пусть х – количество электричества, перешедшее на второй шарик.
Поскольку U  q C , то условие равенства потенциалов запишется в виде:
qx
x
qr2
. Отсюда x 
. Суммарная энергия системы равна:

4 0 r1 4 0 r2
r1  r2
q  x
W
2
x2
. Если энергия принимает минимальное значение, то dW dx  0 и

2C1
2C2
2 q  x  2x
dW
qC2
. Но емкости шаров


0 x
d 2W dx 2  0 . Значит,
dx
2C1
2C2
C1  C2
пропорциональны радиусам. Значит, x  qr2  r1  r2  . При таком значении количества
электричества, переданного от одного шара к другому, потенциалы шаров будут равны. Убедимся, что при этом система будет иметь минимальную энергию:
d 2W 1
1
 
 0.
2
dx
C1 C2
3.3. Постоянный электрический ток
3.3.1. Сила тока
В электродинамике – разделе учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов, – важнейшим понятием является понятие электрического тока. Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. Если в проводнике создать электрическое поле, то носители заряда придут в упорядоченное движение: положительные – в направлении поля, отрицательные – в противоположную сторону.
147
Для возникновения и существования электрического тока необходимо, с
одной стороны, наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно, а с другой стороны, – наличие электрического
поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их
упорядоченное движение. За направление тока условно принимают направление
движения положительных зарядов.
Электрический ток принято характеризовать силой тока – скалярной величиной, равной заряду, переносимому носителями через рассматриваемую поверхность (например, поперечное сечение проводника) в единицу времени i  q .
t
Электрический ток может быть распределен по поверхности, через которую он
течет, неравномерно. В этом случае ток можно охарактеризовать с помощью вектора
плотности тока j , который численно равен силе тока di , текущего через расположенную в данной точке перпендикулярную к направлению движения носителей
площадку dS , отнесенной к величине этой площадки: j  di . За направление векdS
тора j принимается направление движения положительных зарядов.
Ток, не изменяющийся со временем, называется постоянным. Для постоянного тока I  q . В системе СИ единицей силы тока служит ампер. (Определение
t
ампера будет дано позже.)
3.3.2. Электродвижущая сила. Напряжение
Если в проводнике создать электрическое поле и не принять мер для его
поддержания, то перемещение носителей заряда приведет очень быстро к тому,
что поле внутри проводника исчезнет и, следовательно, ток прекратится. Поэтому
для существования постоянного тока необходимо наличие в цепи устройства,
способного создавать и поддерживать разность потенциалов за счет работы сил
неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со
стороны источников тока, называются сторонними.
Природа сторонних сил может быть различной. Например, в гальванических
элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе – за счет механической энергии вращения ротора генератора и т. п. Роль источника тока в электрической цепи такая же, как роль
насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические заряды
движутся внутри источника тока против сил электростатического поля, благодаря
чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.
Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электро148
движущей силой (э. д. с.)  , действующей в цепи:   A . Эта работа произвоq
дится за счет энергии, затрачиваемой в источнике тока, поэтому величину 
называют также электродвижущей силой источника тока, включенного в цепь.
Кроме сторонних сил на заряд q действуют также силы электростатического поля. Значит, работа, совершаемая результирующей силой над зарядом q на
участке цепи от точки 1 до точки 2, будет равна A12  12q  1  2  q . Здесь 1 и
2 – потенциалы в точках 1 и 2 цепи.
Напряжением U на участке цепи 1–2 называется физическая величина,
определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряA
да на данном участке цепи. Значит, U12  12  1  2  12 , т. е. напряжение на
q
концах участка цепи равно разности потенциалов в том случае, если на этом
участке не действует э. д. с.
3.3.3. Закон Ома для однородного участка цепи
Г. Ом экспериментально установил, что сила постоянного тока, текущего по
однородному металлическому проводнику (т. е. по проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
I  U R . Величина R называется электрическим сопротивлением проводника. Измеряется сопротивление в омах: 1Ом – это сопротивление такого проводника, в котором при напряжении в 1 В течет ток в 1 А . Сопротивление зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника R   l S . Здесь l – длина проводника, S – площадь
поперечного сечения,  – удельное электрическое сопротивление.
Величина, обратная сопротивлению G  1 R , называется электрической
проводимостью. Единица проводимости – сименс [ См ]: 1См – проводимость
участка электрической цепи сопротивлением 1Ом .
Удельное сопротивление  в системе СИ измеряется в омо-метрах [ Ом  м ].
Опыт показывает, что в первом приближении изменение удельного сопротивления  , а следовательно, и сопротивления R , с температурой описывается
линейной зависимостью:   0 1   t  ; R  R0 1   t  . Здесь  и  0 , R и R0 –
удельные сопротивления и сопротивления при температурах t C и 0 C ;  – температурный коэффициент сопротивления (для чистых металлов   1 273 К 1 ).
Используя значение  , можно записать:
R  R0 1  t / 273  R0
273  t
T
 R0
 R0T .
273
273
149
Закон Ома для однородного участка цепи можно представить в иной форме:
1
U
U
I 1U
. Величина
называется удельной электрической проI 
 
R l S
S  l

водимостью. Измеряется удельная электрическая проводимость в [ См м ] и обычно обозначается через  .
Так как U l  E – напряженность электрического поля в проводнике, I S –
плотность тока, то закон Ома можно записать в дифференциальной форме j   E ,
связывающей плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Носители тока движутся в направлении вектора Е , поэтому направления векторов j и Е . Таким образом, можно записать j   E .
Пример 1. Можно ли обнаружить различие в сопротивлении медного провода, если температура в помещении понизилась от 30 до 15 С ? Погрешность
при измерении сопротивления считать не превышающей 1% .
Решение. Сопротивление провода при температуре t C составляет
R  R0 1   t  , где R0 – сопротивление при t  0 C и   1 273град1 . Относительное изменение сопротивления при изменении температуры в указанных пределах  R1  R2  R1   t1  t2   273  t1   15 303  0,049 , т. е. 4,9% . При погрешности измерения 1% это изменение будет обнаружено.
Пример 2. Внутреннее сопротивление гальванометра R1  680 Ом . Как и
какое сопротивление нужно подключить к нему, чтобы можно было измерить ток
силой 2,5 А ? Шкала гальванометра рассчитана на 300 мкА .
Решение. Для того чтобы гальванометр с пределом измерения 300 мкА не вышел из строя при измерении тока 2,5 А , большую часть тока необходимо пропустить
через дополнительное сопротивление, подключенное параллельно гальванометру; при
этом I  I1  I 2 (рис. 3.3.1).
Рис. 3.3.1
Подобное дополнительное сопротивление называется шунтом. Потенциалы
в точках подсоединения шунта равны, поэтому, используя закон Ома, имеем:
I1R1  I 2 R2 . (Величина IR в электротехнике называется падением напряжения на
сопротивлении R ). Отсюда R2  R1  I1 I 2   R1  I1  I  I1  .
Подставляя данные задачи, получаем: R2  0,0816 Ом .
150
Пример 3. Внутреннее сопротивление гальванометра R1  720 Ом , шкала
его рассчитана на I  300 мкА . Как и какое добавочное сопротивление нужно
подключить, чтобы можно было измерить им напряжение 300 В ?
Решение. Для измерения напряжения на участке цепи гальванометр подключают параллельно этому участку (рис. 3.3.2). Предельное падение напряжения на
зажимах гальванометра в соответствии с законом Ома равно: U1  IR1  0,216 B .
Рис. 3.3.2
Для того чтобы этим гальванометром измерить напряжение U 2  300 В ,
нужно последовательно с ним подсоединить сопротивление R2 , называемое дополнительным сопротивлением. Величина его должна быть такой, чтобы падение
напряжения на суммарном сопротивлении R1  R2 было равно U 2  300 В . ПоэтоU  IR1
му IR1  IR2  U 2 . Следовательно, R2  2
 106  Ом  .
I
3.3.4. Закон Джоуля–Ленца. Закон Ома
для неоднородного участка
При прохождении по проводнику тока проводник нагревается. Джоуль и
Ленц независимо друг от друга обнаружили экспериментально, что количество
выделяющегося в проводнике тепла пропорционально его сопротивлению, квадрату силы тока и времени прохождения тока: Q  RI 2t . Если сила тока меняется со
временем, то Q   Ri 2 dt . Если сопротивление выразить в Омах, силу тока – в Амперах, время – в секундах, то тепло определяется в Джоулях. Нагревание происходит за счет работы, совершаемой силами поля над носителями заряда.
Зная закон Джоуля – Ленца, можно распространить закон Ома, записанный для
однородного участка цепи, на участок неоднородный, т. е. участок цепи, содержащий
э. д. с. Будем исходить из закона сохранения энергии. Пусть на концах участка, содержащего э. д. с. (рис. 3.3.3), поддерживается разность потенциалов 1  2 .
Рис. 3.3.3
Величину э. д. с. обозначим 12 . Задавшись направлением на участке, будем
считать ток I положительным, если он течет в этом направлении. Аналогично, э. д. с.
будет положительной, если она действует в этом же направлении. (Это значит, что
151
над положительным зарядом, перемещающимся в этом направлении, сторонние силы
совершают положительную работу.)
Если проводник участка неподвижен, то единственный результат прохождения тока – нагревание. Поэтому работа всех сил (электростатических и сторонних), совершенная над носителями заряда, должна быть равна выделившемуся
теплу: dA  12dq  1  2  dq , где dq  Idt – заряд, прошедший за время dt . При
этом выделяется тепло: dQ  I 2 Rdt  IR  Idt   IRdq . Приравнивая выражения для
  2  12
работы и тепла, получаем: IR  1  2   12 , откуда I  1
. Это закон
R
Ома для неоднородного участка цепи. Если 12  0 , то это выражение переходит в
  2 U
закон Ома для однородного участка I  1
 . Если 1   2 (цепь замкнута),
R
R
то I 

( R – полное (суммарное) сопротивление цепи).
R
Пример 4. Разность потенциалов между двумя точками А и В равна 9 В .
Имеются два проводника, сопротивления которых равны соответственно 5 Ом и
3 Ом . Найти количество тепла, выделяющегося в каждом из проводников в 1 с , если
проводники между А и В включены: а) последовательно, б) параллельно (рис 3.3.4).
Рис. 3.3.4
Решение. При последовательном соединении проводников результирующее
сопротивление равно сумме соединяемых сопротивлений: R  R1  R2 . Ток, текущий через такое сопротивление, по закону Ома равен I  U R . В соответствии
с законом Джоуля – Ленца на первом проводнике выделится тепло, равное
U 2 R1
U 2 R2
2
2
Q1  I R1  2  6,33 Дж ; на втором – Q2  I R2  2  3,80  Дж  .
R
R
При параллельном соединении проводников падения напряжения на каждом
из проводников одинаковы и равны 9 B . Поэтому токи, текущие через каждый
проводник, составят: I1  U R1 и I 2  U R2 . По закону Джоуля–Ленца:
Q1  I12 R1  U 2 R1  16,2 Дж и Q2  U 2 R2  27,0 Дж .
Пример 5. На схеме (рис. 3.3.5) сопротивление R  1,4 Ом , 1 и  2 – два
элемента, э. д. с. которых одинаковы и равны:   2 В . Внутренние сопротивления
152
этих элементов равны, соответственно, r1  1 Ом и r2  1,5 Ом . Найти силу тока в
каждом из элементов и во всей цепи.
Рис. 3.3.5
Решение. Поскольку элементы соединены параллельно и э. д. с. их одинаковы, суммарная э. д. с., развиваемая такой батареей, равна э. д. с. каждого из них.
Результирующее внутреннее сопротивление элементов при параллельном соедиrr
нении составляет R  1 2 . Полное сопротивление цепи – R  R . В соответr1  r2
ствии с законом Ома для замкнутой цепи через сопротивление R и элементы течет суммарный ток I     R  R   1 A . Падение напряжения на сопротивлении
R равно U1  I  R  1,4  B  . Отсюда падение напряжения на внутренних сопротивлениях элементов составляет U 2    U1  0,6( B) . Тогда ток в первом элементе
I1  U 2 r1  0,6( A) ; во втором элементе – I 2  U 2 r2  0,4( A) .
3.3.5. Правила Кирхгофа
Закон Ома позволяет рассчитать практически любую электрическую цепь.
Однако расчет значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом. Этих правил два.
Первое относится к узлам цепи. Узлом называется точка, в которой сходится не
менее трех проводников (рис. 3.3.6). Ток, текущий к узлу, считается положительным;
ток, вытекающий из узла, – отрицательным. Первое правило Кирхгофа гласит: алгебраическая сумма токов, сходящихся в узле, равна нулю:  I k  0 . Это правило вытеk
кает из закона сохранения электрического заряда. Если бы алгебраическая сумма токов была отлична от нуля, в узле происходило бы накапливание или уменьшение заряда. Это приводило бы к изменению потенциала узла и изменению текущих в цепи
токов. Значит, для того чтобы токи в цепи были постоянными, должно выполняться
первое правило Кирхгофа.
Рис. 3.3.6
153
Первое правило Кирхгофа может быть применено к каждому из N узлов цепи, но независимыми будут только (N – 1) уравнения; одно уравнение может быть
получено с помощью комбинации всех остальных.
Для обоснования второго правила Кирхгофа выделим мысленно в разветвленной цепи произвольный замкнутый контур (например, контур 1–2–3–4–1,
рис. 3.3.7). Зададимся произвольно направлением обхода, например, по часовой
стрелке, и применим к каждому из неразветвленных участков закон Ома:
I1R1  1  2  1 ,
I 2 R2  2  3   2 ,
I 3 R3  3  4  3 ,
I 4 R4  4  1   4 .
Сложим полученные уравнения:
 I k Rk    k . Последнее равенство выраk
k
жает второе правило Кирхгофа: сумма падений напряжений на всех участках замкнутого контура равна сумме действующих в контуре э. д. с.
Уравнение по второму правилу Кирхгофа может быть составлено для всех замкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи.
Но независимыми будут только уравнения для тех контуров, которые нельзя получить
наложением других контуров друг на друга.
Рис. 3.3.7
При составлении уравнений по второму правилу Кирхгофа токам и э. д. с.
нужно приписывать знаки в соответствии с выбранным направлением обхода
контура. Ток во внешней цепи течет от положительного полюса источника к отрицательному, а внутри источника – от отрицательного к положительному. Если
во внешней цепи ток течет навстречу выбранному направлению обхода контура,
то его нужно считать отрицательным, если ток течет по направлению обхода, то
его нужно считать положительным. Аналогично, э. д. с. следует считать отрицательной, если она действует в направлении, противоположном выбранному
направлению обхода.
Направления обхода в каждом из контуров выбираются произвольно и независимо от выбора направлений в других контурах. При этом может случиться, что
один и тот же ток (или одна и та же э. д. с.) войдет в разные уравнения с разными
154
знаками. Это не имеет значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении на обратные.
Составляя уравнения по второму правилу Кирхгофа, следует помнить, что
через любое сечение неразветвленного участка цепи течет один и тот же ток.
Число независимых уравнений, составленных в соответствии с первым и
вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому если заданы э. д. с. и сопротивления всех неразветвленных участков, то могут быть вычислены все токи. Можно решать задачи и другого рода, например, найти э. д. с., которые нужно включить в каждый из
участков цепи, чтобы получить при заданных сопротивлениях нужные токи.
Пример 6. На схеме (рис. 3.3.8) даны R1 , R2 , R3 , 1 , 3 . Необходимо найти  2 ,
при которой I 2  1 A , и получающиеся при этом токи I1 и I 3 .
Рис. 3.3.8
Цепь имеет два узла (точки 3 и 6) и в ней можно выделить три замкнутых
контура (1–2–3–6–1; 3–4–5–6–3; 1–2–4–5–1). Уравнения, составленные по первому правилу Кирхгофа для обоих узлов, не будут независимыми. Действительно,
для указанных на схеме направлений токов имеем: для узла 3  I1  I 2  I 3  0 ; для
узла 6 I1  I 2  I 3  0 . Очевидно, что любое из этих уравнений можно получить из
другого заменой знаков на обратные. (В дальнейшем будем использовать первое
из них.)
Любой из трех указанных контуров может быть получен наложением двух
других контуров. Значит, только два уравнения, составленные по второму правилу Кирхгофа, будут линейно не зависимы. Используем контуры 1–2–3–6–1 и 3–4–
5–6–3. Зададимся на этих контурах направлениями обхода (произвольно, например, как на рисунке) и составим уравнения, учитывая, что внутри источников носители зарядов движутся от минуса к плюсу: для контура 1–2–3–6–1:
 I1R1  I 2 R2  1   2 ; для контура 3–4–5–6–3: I 3 R3  I 2 R2  3   2 . (Уравнение,
составленное для контура 1–2–4–5–1, будет линейной комбинацией последних
двух уравнений.)
Подставляя числовые значения в полученные уравнения, получаем:
155
1  I1  1  I 3  0  2  1
2  I1  0  I 3  1  2  4
0  I1  3  I 3  1  2  1.
Система трех уравнений с тремя неизвестными I1 , I 3 ,  2 легко решается,
например, по правилу Крамера:
1  1  1
1  1  0
1  1  0
2  0  4
4  0  1
2  4  1
0  3  1
1  3  1
0  1  1
2 
 1,6( В) ; I1 
 1,2( A) ; I 3 
 0,2( А) .
1  1  0
1  1  0
1  1  0
2  0  1
2  0  1
2  0  1
0  3  1
0  3  1
0  3  1
Для  2 получено отрицательное значение. Это означает, что направление
действия  2 должно быть противоположным показанному на рисунке, которое
принималось при расчете. Ток I 3 также будет течь не в направлении 3–4, как указано на рисунке, а в противоположном направлении.
3.3.6. Расчет мощности, выделяемой в цепи
Расчет электрической цепи включает в себя не только определение токов и
напряжений на отдельных участках, но и определение мощности, выделяемой в цепи.
Электрическая цепь включает в себя источник тока, подводящие провода и потребителя тока. Каждый из этих элементов обладает сопротивлением. Как правило,
сопротивление подводящих проводов мало по сравнению с сопротивлением источника тока и потребителя (нагрузки), поэтому почти всегда в расчетах его не учитывают.
Как мы уже знаем, сила тока в замкнутой цепи равна: I 

, где r – сопроRr
тивление источника, R – сопротивление нагрузки. В замкнутой цепи напряжение на
R
нагрузке одинаково с напряжением на зажимах э. д. с. и равно: U  IR  
.
Rr
Напряжение на нагрузке меньше э. д. с. При разомкнутой цепи ( R   ) получаем
U   , т. е. напряжение на зажимах разомкнутого источника равно его э.д.с.
Поскольку работа по переносу заряда q вдоль замкнутой цепи равна:
A
q
A   q , то мощность, развиваемая источником составит: P      I . Значит,
t
t
мощность, развиваемая источником, равна произведению э. д. с. на силу тока. Ис2
пользуя выражение для силы тока в замкнутой цепи, получаем P 
. На
Rr
нагрузке выделяется только часть этой мощности:
156
A RI 2t
2
2
R
2
Pн  
 RI 
R
.
2
t
t
(R  r)
Rr Rr
R
 1, Pн  P . Мощность Pн называется полезной мощностью.
Rr
Остальная мощность, выделяемая в источнике и проводах, бесполезна. Отношение полезной мощности ко всей мощности, развиваемой источником, называется
P
R
коэффициентом полезного действия (к. п. д.) источника:   н 
. Из выраР Rr
жения видно, что для увеличения к. п. д. сопротивление источника следует делать
как можно меньшим.
Мощность, развиваемая данным источником, зависит от сопротивления
нагрузки. При коротком замыкании ( R  0 ) она максимальна, но в этом случае вся
мощность выделяется в источнике и бесполезна. С ростом сопротивления нагрузки полная мощность убывает, стремясь к нулю.
Рассмотрим случай, когда полезная мощность, отбираемая от источника, максимальна. Продифференцируем выражение для полезной мощности по R и приравняем производную нулю:
dPн
rR
2
 0.
3
dR
r  R
Поскольку
Из выражения видно, полезная мощность максимальна при R  r . (При R  
полная мощность и, следовательно, полезная мощность равны нулю.) К. п. д. источника в этом случае равен 0,5 .
Пример 7. К двум батареям, соединенным параллельно, подключили электролампу. Каким сопротивлением должна она обладать, чтобы мощность ее была
максимальной, если э. д. с. батарейравны: 1  12 В ,  2  10 В , их внутренние сопротивления r1  r2  1 Ом ?
Решение. Составляем уравнения Кирхгофа (рис. 3.3.9). Для контура 1–2–5–
6: I1  I 2  2 ; для контура 1–3–4–6: I1  I 3r3  12 ; для узла 5: I1  I 2  I 3 .
Рис. 3.3.9
Выразим I 3 через r3 . Из первого и третьего уравнений: I1   I 3  2  2 . Из
второго уравнения: I 3  22  2r3  1 . Тогда мощность P  484r3
мощность
максимальна,
то
первая
157
производная
по
r3
 2r3  1
равна
2
. Если
нулю:
dP  2r3  1  484  484r3  4  2r3  1
1

. Отсюда r3  Ом . Взяв вторую производ4
dr3
2
 2r3  1
2
ную, убеждаемся, что она положительна. Значит, найденному значению r3 соответствует максимум мощности.
3.3.7. Электрический ток в различных средах
1. Электрический ток в металлах и полупроводниках.
Ток в металлах вызывается весьма малой разностью потенциалов. Опытным
путем было установлено, что носителями тока являются электроны, которые перемещаются по металлу практически свободно. Концентрация свободных электронов может быть оценена следующим образом. Свободные электроны появляются при отрыве от атомов металла валентных электронов. Если от каждого атома
оторвется хотя бы по одному электрону, их концентрация будет равна количеству
атомов в единице объема 10281029м–3.
Исходя из представлений о свободных электронах, Друде предположил, что
электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершенно свободно,
проходя в среднем некоторый путь  . Но в отличие от молекул электроны соударяются не друг с другом, а с ионами кристаллической решетки. Эти столкновения
приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Представляя поток электронов электронным газом по
молекулярно-кинетической теории, можно оценить среднюю скорость теплового
8kT
движения электронов: v 
. (При T  300 K  v  105 м / с .)
m
При включении электрического поля на хаотическое тепловое движение,
происходящее со скоростью v , накладывается упорядоченное движение электронов с некоторой скоростью u . Величину этой скорости легко оценить из зависимости плотности тока j от концентрации электронов n , их заряда e и средней скорости направленного движения u : j  ne u . (Это вытекает из следуюI q nelS
 ne u ).
щего: j   
S tS
tS
Для оценки примем j равной предельно допустимой техническими нормами для медных проводов: j  107 A 2 . Концентрацию электронов положим равм
29 3
ной n  10 м . Тогда, учитывая, что е  1,6 1019 Кл , для средней скорости получим u  103 м / с .
Таким образом, средняя скорость упорядоченного движения u в 108 раз
меньше средней скорости теплового движения v .
Если бы электроны не сталкивались с ионами, то средняя длина их свободного пробега  и, следовательно, электропроводимость металла, были бы беско158
нечно большими. Электрическое сопротивление металла обусловлено соударениями электронов с ионами.
В классической теории металлов считается, что электроны проводимости
могут обладать любыми значениями энергии. Согласно квантовой теории, энергия
электронов в любом кристаллическом теле, в том числе и в металлах, может принимать лишь дискретные значения, т. е. квантуется. Эти дозволенные значения
энергии называются энергетическими уровнями. Дозволенные значения энергии
электронов в кристалле объединяются в зоны, разделенные промежутками, в которых разрешенных значений энергии нет. Эти промежутки называются запрещенными зонами. Ширина разрешенных и запрещенных зон не зависит от размера
кристалла. Измеряется она в единицах энергии и имеет порядок нескольких электрон-вольт (1эВ  1,6 1019 Дж ).
При температуре, равной абсолютному нулю, энергия кристалла должна
быть минимальной. Поэтому электроны, наиболее удаленные от ядер атомов (валентные электроны) заполняют попарно нижние уровни своей разрешенной зоны.
Эта разрешенная зона называется валентной. Более высокие разрешенные зоны
будут от электронов свободны.
В зависимости от степени заполнения валентной зоны электронами и ширины запрещенной зоны возможны три случая (рис. 3.3.10):
а) электроны заполняют валентную зону не полностью. Расстояния между
энергетическими уровнями в зоне невелики ( 1023 1022 эв ), поэтому достаточно
сообщить электронам небольшую энергию, чтобы перевести их на более высокие
уровни. Для этого достаточно энергии теплового движения. Следовательно, при
температурах, отличных от 0 К , часть электронов находится на верхних уровнях.
Эти электроны легко могут ускоряться электрическим полем. Кристалл с подобной схемой энергетических уровней представляет собой металл;
б) и в) уровни валентной зоны полностью заняты электронами – зона заполнена. Для того чтобы увеличить энергию электрона, необходимо сообщить ему
количество энергии, не меньшее, чем ширина запрещенной зоны W . При этих
условиях свойства кристалла определяются шириной запрещенной зоны. Если
W не превосходит одного электрон-вольта, энергии теплового движения оказывается достаточно для того, чтобы перевести часть электронов в верхнюю свободную зону, эти электроны будут находиться в условиях, аналогичных тем, в которых находятся валентные электроны в металле. Свободная зона окажется для них
зоной проводимости. Такое вещество называется электронным полупроводником.
Если ширина запрещенной зоны W велика (порядка нескольких электронвольт), тепловое движение не сможет забросить в свободную зону заметное число
электронов. В этом случае кристалл оказывается изолятором.
159
Рис. 3.3.10
Таким образом, зонная теория твердых тел позволяет с единой точки зрения
истолковать существование металлов, диэлектриков и полупроводников, объясняя
различие в их электрических свойствах, во-первых, неодинаковым заполнением
электронами разрешенных зон и, во-вторых, шириной запрещенных зон.
2. Электрический ток в электролитах.
Прохождение тока через металлы не сопровождается какими-либо превращениями. Такие проводники называются проводниками 1-го рода. Вещества, в
которых при прохождении тока происходят химические превращения, называются проводниками 2-го рода или электролитами. К их числу принадлежат растворы солей, щелочей и кислот в воде и некоторых других жидкостях, т. е. вещества,
распадающиеся в растворе на ионы. Носителями заряда в электролитических растворах являются ионы. Чтобы выяснить, каким образом происходит диссоциация,
рассмотрим полярную молекулу NaCl. При объединении атомов Na и Cl в молекулу происходит перераспределение электронов – валентный электрон натрия
оказывается как бы включенным в оболочку атома хлора, для полной застройки
которой не хватает как раз одного электрона. В результате атом натрия превращается в положительный ион, атом хлора – в отрицательный ион. Оба иона удерживаются в молекуле силами кулоновского взаимодействия. Эта связь под действием молекул растворителя может быть разрушена, и в этом случае молекула разделяется на два иона противоположного знака (диссоциирует). Диссоциация молекул проходит интенсивнее в жидкостях с большей диэлектрической проницаемостью. Из всех жидкостей  (диэлектрическая проницаемость) больше всего у воды. Поэтому диссоциация молекул в водных растворах особенно велика.
Степень диссоциации вещества характеризуется коэффициентом диссоциации  , показывающим, какая часть молекул растворенного вещества находится в
диссоциированном состоянии. Если количество молекул растворенного вещества,
содержащихся в единице объема раствора равно n , то n   n будут находиться в
растворе в виде ионов и n  1    n – в виде недиссоциированных молекул.
160
Если в раствор поместить металлические или угольные электроды и присоединить их к полюсам генератора постоянного напряжения (рис. 3.3.11), то между
электродами образуется электрическое поле. В этом поле скорость ионов получает
составляющую в направлении действия поля. Это движение ионов образует электрический ток. Движение происходит по всему объему, скорости невелики, т. к.
ионы постоянно сталкиваются с молекулами растворителя и не распавшимися молекулами растворенного вещества. Скорость ионов, отнесенную к единице напряженности поля, называют подвижностью ионов. С повышением температуры подвижность ионов возрастает, следовательно, вязкость растворов уменьшается.
Рис. 3.3.11
Передвигаясь в растворе, ионы достигают электродов и, нейтрализуя заряды, превращаются в атомы соответствующего вещества. На аноде отрицательные
ионы отдают лишние электроны, которые поступают во внешнюю цепь и поддерживают ток в ней. На катоде положительные ионы присоединяют электроны, поступающие из внешней цепи.
Таким образом, при прохождении тока через электролит происходит постепенное убывание ионов из раствора. Количество ионов пополняется за счет дальнейшей диссоциации молекул растворенного вещества. Пока средняя концентрация ионов в растворе неизменна, сила тока подчиняется закону Ома.
Процессы разложения электролита с выделением соответствующих веществ
на электродах, которые происходят под действием электрического поля, называются электролизом. Законы электролиза были экспериментально установлены
Фарадеем и носят его имя.
1 закон Фарадея: масса выделившегося на электроде вещества пропорциональна заряду, протекшему через электролит m  Kq . Для постоянного тока
q  It , поэтому m  KIt . Коэффициент пропорциональности K зависти от природы вещества и называется электрохимическим эквивалентом этого вещества. При
q  1 имеем m  K (численно). Значит, электрохимический эквивалент представляет собой массу вещества, выделяющегося на электроде при прохождении через
электролит заряда, равного единице.
2 закон Фарадея. Этот закон связывает электрохимический эквивалент с его
химическим эквивалентом. Химическим эквивалентом называется безразмерная
величина, численно равная массе данного элемента, выраженной в граммах (или в
161
килограммах), которая замещает в химических соединениях 1,0078 г (или кг) водорода. (Валентностью элемента Z называется число атомов водорода, которое
замещается в химических соединениях одним атомом данного элемента.) Для одновалентного элемента химический эквивалент равен его атомному весу. Для Zвалентного элемента химический эквивалент равен атомному весу, деленному на
 A
валентность   . Второй закон Фарадея гласит: электрохимические эквиваленты
Z
1 A 1
всех веществ пропорциональны их химическим эквивалентам: K 
( – коFZ F
эффициент пропорциональности). Величину F называют числом Фарадея.
Aq
Объединяя оба закона Фарадея, получим: m 
. При q  F масса m
ZF
численно совпадает с A Z . Количество элемента, масса которого (выраженная в
граммах) численно равна химическому эквиваленту, называется граммэквивалентом. Количество вещества, масса которого равна A Z килограммов,
называется килограмм-эквивалентом. Таким образом, для выделения на электроде
килограмм-эквивалента или грамм-эквивалента любого вещества, требуется пропустить через электролит один и тот же заряд, равный F . Опытным путем устаКл
Кл
новлено: F  96,497  106
или F  96497
.
кг  экв
г  экв
Пример 8. При пропускании через электролит тока I  1,5 A в течение
20 мин на катоде выделилось 594 мг вещества. Какое это вещество?
Решение. По первому закону Фарадея имеем: m  KIt . Отсюда
K  m  It   594 1,5  20  60   0,33 мг Кл . Такое значение имеет электрохимический эквивалент меди.
3. Электрический ток в газах.
Прохождение электрического тока через газы называется газовым разрядом. В
металлах и электролитах носители заряда существуют всегда, независимо от прохождения тока; электрическое поле обусловливает лишь упорядоченное движение
зарядов. Газы в нормальном состоянии являются изоляторами. Носители тока в них
отсутствуют. Лишь при соблюдении специальных условий в газах могут появиться
носители заряда (ионы, электроны) и возникнуть электрический разряд.
Наложим на газоразрядную трубку небольшое напряжение. Если внешний
ионизатор отсутствует, ток через трубку не пойдет. Таким образом, для того чтобы стать проводником электричества, газ должен быть ионизован, т. е. должно
произойти расщепление нейтральных атомов и молекул на ионы и свободные
электроны. Под действием какого-либо ионизатора происходит вырывание из
электронной оболочки атома или молекулы одного или нескольких электронов.
Это приводит к образованию свободных электронов и ионов.
При наложении поля заряженные частицы будут направляться к электродам. Это явление называется несамостоятельным разрядом. Несамостоятельный
162
разряд может быть вызван нагреванием газа до высокой температуры (термическая ионизация); воздействием ультразвукового или рентгеновского излучения, а
также радиоактивного излучения.
При повышении напряжения на трубке все ионы, создаваемые ионизатором,
доходят до электродов. Дальнейшее увеличение напряжения не может увеличить
тока. Сила тока насыщения равна заряду ионов, образуемых ионизатором за одну
секунду в объеме газоразрядной трубки. На начальном участке зависимости I  u 
(при малых напряжениях) сила тока пропорциональна напряжению, т. е. выполняется закон Ома. Ток насыщения является мерой ионизирующего действия ионизатора. Если в режиме пропорциональности тока напряжению или в режиме тока
насыщения прекратить действие ионизатора, то прекратится и разряд.
При дальнейшем увеличении напряжения в некоторый момент времени
энергия электронов, движущихся к катоду, увеличивается настолько, что, налетая
на нейтральные молекулы, они способны выбить из них дополнительные электроны. Выбивание электронов из нейтральных молекул приводит к тому, что число ионов и электронов лавинообразно возрастает, и разряд становится самостоятельным, т. е. сохраняется после прекращения действия ионизатора. Напряжение,
при котором возникает самостоятельный разряд, называется напряжением пробоя.
Выделяют четыре типа самостоятельного разряда.
А. Тлеющий разряд возникает при низких давлениях и имеет характерный
вид для каждого давления (можно по внешнему виду разряда определить давление газа). Используется в газосветных трубках рекламы.
Б. Дуговой – наблюдается в электрической дуге. В дуговом разряде плотность тока велика, хотя напряжение между электродами мало. При дуговом разряде температура электродов очень высока, поэтому в дуге большую роль играет
термоэмиссия электронов с катода.
В. Искровой разряд возникает при больших напряженностях электрического
поля  3  106 В м ) под давлением 105 Па . Искра имеет вид ярко светящегося
тонкого канала. Используется искра при воспламенении горючей смеси, электроискровой точной обработке металлов и т. п.
Г. Коронный – возникает при высоком давлении газа на остриях, тонких
проводах и везде, где есть резкое падение потенциала, а, значит, высока напряженность поля до  3  106 В м ). Свечение имеет вид короны (отсюда и название).
3.3.8. Термоэлектронные явления
Прохождение тока через металлы и полупроводники иногда сопровождается
явлениями, которые получили название термоэлектронных.
Явление Зеебека. Это явление заключается в том, что в замкнутой цепи, образованной двумя разнородными металлами, возникает электрический ток, в случае если спаи этих металлов поддерживать при разных температурах. Первая причина этого явления в том, что по обе стороны от контакта двух разнородных металлов возникает скачок потенциала – контактная разность потенциалов. Другая
причина в том, что при наличии градиента температуры вдоль проводника элек163
троны, участвующие в тепловом движении, распределятся вдоль проводника: возле горячего конца соберутся электроны с высокой энергией (более быстрые), возле холодного конца – более медленные электроны. Это повлечет за собой диффузию быстрых электронов к холодному концу, медленных электронов – к горячему
концу. Диффузионный поток быстрых электронов будет больше, поэтому у холодного конца образуется избыток электронов, а у горячего – их недостаток. В
проводнике возникнет электрическое поле, направленное навстречу градиенту
температуры. Это поле будет увеличивать поток медленных электронов, движущихся по полю, и уменьшать поток быстрых электронов, движущихся против поля. Так будет продолжаться до тех пор, пока потоки не уравняются. Между концами проводника возникнет разность потенциалов.
Указанные причины приводят к возникновению в замкнутой цепи, состоящей из двух разнородных проводников, электродвижущей силы, называемой
термоэлектродвижущей силой.
Явление Зеебека используется для измерения температур. Соответствующее
устройство называется термопарой. Один спай термопары поддерживают при постоянной температуре, другой помещают в тот объем, температуру которого хотят измерить. О величине температуры судят по измерению возникающей термоэлектродвижущей силы.
Явление Пельтье. Это явление по своей сути обратно явлению Зеебека и заключается в том, что при протекании тока через цепь, составленную из разнородных
проводников, в одних спаях происходит выделение, а в других – поглощение тепла.
Явление Пельтье имеет следующее объяснение. Носители тока по обе стороны от спая имеют различную энергию. Если носители, пройдя через спай, попадают в область с меньшей энергией, они отдают избыток энергии кристаллической решетке, в результате чего спай нагревается. На другом спае носители переходят в область с меньшей энергией. Недостающую энергию они заимствуют у
решетки, что приводит к охлаждению спая.
Широкого применения рассматриваемое явление пока не нашло, хотя доказана принципиальная возможность его использования для создания холодильных
установок и регулирования температуры в помещениях.
Явление Томсона. Тепло, аналогичное теплу Пельтье, должно выделяться
или поглощаться при прохождении тока по однородному проводнику, вдоль которого имеется градиент температуры. Этот эффект действительно был обнаружен экспериментально и получил название эффекта Томсона.
Объясняется эффект Томсона аналогично явлению Пельтье. Если ток течет
в направлении возрастания температуры, то электроны при своем движении будут
переходить от мест с более высокой температурой (с большей средней энергией
электронов) к местам с более низкой температурой (с меньшей средней энергией
электронов). Избыток своей энергии электроны отдадут решетке, что приведет к
выделению тепла.
164
3.4. Магнитное поле в вакууме и веществе
3.4.1. Характеристики магнитного поля
Электрические токи взаимодействуют друг с другом: два прямых проводника, по которым текут токи одинакового направления, притягивают друг друга; при
токах противоположного направления проводники отталкиваются.
Взаимодействие токов осуществляется через поле, которое называется магнитным. (Это поле оказывает ориентирующее действие на магнитную стрелку.)
Значит, движущиеся заряды создают в пространстве магнитное поле, которое
проявляется в том, что действует на движущиеся в нем заряды.
Для исследования магнитного поля используется замкнутый плоский контур с током, размерами которого можно пренебречь по сравнению с расстоянием
до токов, образующих поле. Здесь имеется полная аналогия с исследованием
электрического поля с помощью точечного заряда. Ориентация контура в пространстве характеризуется направлением нормали к контуру, связанной с направлением тока в контуре правилом правого винта, т. е. за положительное направление нормали принимается направление поступательного движения винта, головка
которого вращается в направлении тока, текущего в контуре.
Поле оказывает на контур ориентирующее действие, устанавливая его положительной нормалью в определенном направлении. Это направление принимается за направление поля.
Если контур установить так, чтобы направления нормали и поля не совпадали, возникнет вращательный момент, стремящийся повернуть контур до равновесного положения. Вращательный момент максимален  М  М max  , если угол
между нормалью к контуру и направлением поля    2 , и М  0 , если   0 .
Опытным путем обнаружено, что максимальное значение вращающего момента пропорционально току, текущему в контуре, и площади контура М  IS .
Величина Pm  IS называется магнитным моментом контура. Эта величина векторная, и направление вектора Pm совпадает с направлением положительной нормали к контуру Pm  ISn (здесь n – единичный вектор положительной нормали).
На пробные контуры, различающиеся значениями Pm , в данной точке поля
действуют разные по величине вращательные моменты М max . Однако отношение
М max Pm для всех контуров будет одно и то же. Это отношение принято за характеристику магнитного поля и называется магнитной индукцией B  M max Pm .
Магнитная индукция – вектор, направленный по направлению магнитного поля.
Поле вектора В наглядно можно представить с помощью линий магнитной индукции, которые строятся аналогично линиям напряженности электрического поля. Линии магнитной индукции всегда замкнуты. Каждая линия B пересекает замкнутую поверхность четное число раз, причем она входит внутрь поверхности
столько же раз, сколько выходит наружу. Поэтому поток вектора магнитной индукции через любую замкнутую поверхность будет равен нулю:
165
Ф   BdS   Вn dS   BdS   0 . Это выражение определяет теорему Гаусса для
S
S
S
вектора магнитной индукции.
Магнитная индукция характеризует силовое действие поля на ток и, следовательно, является аналогом напряженности электрического поля. Наряду с магнитной индукцией В для описания магнитного поля вводится величина Н , называемая напряженностью магнитного поля. Для вакуума: Н  В 0 , где
гн
0  4 107
– магнитная постоянная.
м
Теорема Гаусса справедлива и для вектора напряженности магнитного поля
в вакууме. Для вектора Н в веществе в общем случае это неверно.
3.4.2. Закон Био–Савара–Лапласа
В 1820 г. французские ученые Био и Савар провели исследование магнитных
полей токов различной формы. Лаплас обработал математически их экспериментальные данные и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока. По Лапласу, магнитная индукция поля, создаваемого элементом тока dl ,
 I  dl , r 
равна: dB  0  3  . Модуль вектора dB определяется выражением:
4
r
 Idl
dB 1 Idl
dB  0 2 Sin . (Для напряженности магнитного поля dH 

Sin ).
4 r
0 4 r 2
Здесь dl – длина участка проводника с током, I – сила тока, r – расстояние от элемента с током до точки поля, в которой определяется dB или dH ,  – угол между векторами dl и r .
Из выражения для напряженности магнитного поля следует, что она имеет
размерность, равную размерности силы тока, деленной на размерность длины. В
системе СИ эта единица называется ампер на метр  А м  . Единица магнитной
индукции в системе СИ называется тесла ( Тл ).
Численное значение магнитной индукции в  0 раз больше численного значения напряженности. Следовательно, при напряженности магнитного поля в вакууме, равной 1А м , магнитная индукция составляет 4 107 Тл .
Расчет поля по формуле Лапласа довольно сложен. Но в отдельных частных
случаях закон Био–Савара–Лапласа и принцип суперпозиции позволяют довольно
просто рассчитать конкретное поле. Например, для магнитного поля прямого тока, т. е. тока, текущего по тонкому прямому проводнику бесконечной длины (рис.
3.4.1), имеем: r  b Sin ; dl  rd Sin  bd Sin 2 . (Индукцию будем вычислять
в точке, отстоящей от проводника на расстоянии b .)
166
Рис. 3.4.1
Как известно, вектор, определяемый векторным произведением, перпендикулярен плоскости, проходящей через векторы-сомножители. Следовательно, в нашем
случае все векторы dB имеют одинаковое направление (за чертеж). Из закона Био–
I
dB  0 Sin d .
Савара–Лапласа
Для
напряженности
аналогично:
4 b
1 I
dH 
Sin d . Угол  изменяется от 0 до  . Интегрирование по углу  дает:
4 b
I
 2I
I 
I
B   dB  0  Sin d  0
Sin

d


. (Аналогично – H   dH 
.)
4 b 0
4 b
4 b 0
2 b
Совершенно несложно вычисляется напряженность магнитного поля в центре кругового тока (тока, текущего по проводнику, имеющему форму окружности
радиусом R ). Каждый элемент тока создает в центре магнитное поле, направленное вдоль положительной нормали к контуру (рис. 3.4.2).
Рис. 3.4.2
Следовательно, векторное сложение векторов dB сводится к сложению их
модулей. Поскольку    2 , то, используя выражение для dB , имеем:
 I
 I
I
B   dB  0 2  dl  0 2 2 R  0 .
4 R
4 R
2R
Теперь найдем Н на оси кругового тока на расстоянии х от плоскости, в
которой лежит контур с током. Векторы dB должны быть перпендикулярны к
плоскостям, проходящим через соответствующие векторы dl и r . Следовательно, они образуют симметричный конический веер (рис. 3.4.3).
167
Рис. 3.4.3
Из соображений симметрии ясно, что результирующий вектор B направлен
вдоль оси тока. Каждый из составляющих векторов dB вносит в результирующий
R
вектор вклад dBII , равный по модулю dBSin  dB . Угол  между векторами
r
R  Idl R  IRdl
dl и r прямой, поэтому dBII  dB  0 2  0 3 .
r 4 r r 4 r
Интегрируя по всему контуру и учитывая, что r  R 2  x 2 , получаем:
 IR
 IR

2 R 2 I
. При x  0 эта формула перехоB   dB  0 3  dl  0 3 2 R  9
4 r
4 r
4 R 2  x 2 3 2


дит в выражение для напряженности поля в центре кругового тока.
Пример 1. По двум параллельным бесконечно длинным проводникам, находящимся на расстоянии d  10 см друг от друга, текут токи противоположного
направления I  30 A . Определить магнитную индукцию поля в точке, расположенной посредине между проводниками. Чему равна индукция поля в точке, которая
находится на расстоянии r1  15 см от одного и r2  5 см от другого проводника?
Решение. Индукция магнитного поля, создаваемого прямым током I , равна
I
B  0 , где R – расстояние от тока до исследуемой точки поля. Линии магнит2 R
ной индукции прямого тока – концентрические окружности (рис. 3.4.4).
Рис. 3.4.4
Направление вектора магнитной индукции перпендикулярно плоскости,
проходящей через направление тока и радиус-вектор, проведенный от тока в данную точку поля. Ясно, что в точке посередине между проводниками направления
векторов магнитной индукции полей, создаваемых первым и вторым токами, одинаковы, т. е. результирующая индукция равна их сумме:
168
0
4    10760
B 
 2,4  104 (Тл) .
 I1  I 2  
2  d 2 
2    0,05
В точке, отстоящей от первого и второго токов на расстояниях r1 и r2 , соответственно, суммарная индукция определится векторной суммой векторов индукции, создаваемых первым и вторым токами. Направлены эти векторы по касательным к соответствующим окружностям, следовательно, противоположно друг другу:
I
B1  0 1  4  105 (Тл) ; B2  12  105 (Тл) .
2 r1
Модуль результирующей индукции будет равен их разности:
B  8  10 5 Тл .
Пример 2. Прямой бесконечный проводник имеет круговую петлю радиусом R  80 см (рис. 3.4.5). Определить силу тока в проводнике, если известно, что
в точке А магнитная индукция В  12,5 мкТл .
Рис. 3.4.5
Решение. Направления векторов магнитной индукции полей, создаваемых прямым и круговым токами, в точке А совпадают. Значит, модуль результирующей индукции определится суммой модулей этих векторов:
4 10 7 I
4 107 I
; B2 
.
В1 
2R
2 R
4  107  I   1
2 RB
2  08  12,5  106
I 

 12,1 A  .
Отсюда B 
2R
4  107   1
16,56  107
Расчет магнитного поля соленоида
Напряженность и магнитная индукция магнитного поля сложно зависят от размеров и формы проводника, по которому проходит ток. В некоторых случаях эти
зависимости сравнительно просты, например, легко считается поле внутри соленоида и тороида.
Длинную цилиндрическую катушку, состоящую из некоторого числа витков
проволоки, намотанной по спирали, называют соленоидом. Катушка, намотанная
на каркас, имеющий форму тора, называется тороидом.
Расчет магнитного поля соленоида и тороида основан на теореме о циркуляции вектора магнитной индукции. Циркуляцией вектора магнитной индукции B по
169
заданному замкнутому контуру L называется интеграл
 Bdl   Bl dl . Рассмотрим
L
L
случай, когда контур лежит в плоскости, перпендикулярной к току (рис. 3.4.6). В
каждой точке контура вектор B направлен по касательной к соответствующей
окружности. Так как Bdl  Bl dl  BdlB (свойство скалярного произведения векторов), мы можем заменить Bl dl через BdlB . Но dlB  Rd , где R – расстояние от
прямого тока до dl , а d – угол, на который поворачивается радиальная прямая
при перемещении вдоль контура на отрезок dl . Таким образом, имеем:
I
 Id
Bl dl  BdlB  0 Rd  0
.
2 R
2
I
Значит, циркуляция равна:  Bl dl  0  d . При обходе по контуру, охва2 L
L
тывающему ток, радиальная прямая все время поворачивается в одном направлении, поэтому  d  2 .
L
Рис. 3.4.6
Если контур не охватывает ток, то при обходе по контуру радиальная прямая сначала поворачивается в одном направлении (рис. 3.4.7), а затем в противоположном, поэтому  d  0 . Учитывая это, можно написать  Bl dl  0 I , где под
L
I следует понимать ток, охватываемый контуром. Если контур не охватывает ток,
то циркуляция вектора B равна нулю.
Рис. 3.4.7
Если контур имеет произвольную форму, то вместо радиальной прямой
нужно рассматривать ее проекцию на перпендикулярную к току плоскость.
Если контур охватывает несколько токов, то циркуляция вектора B равна
их алгебраической сумме, умноженной на магнитную постоянную  Bl dl  0  I .
L
170
Воспользовавшись последним выражением, несложно вычислить магнитную
индукцию поля бесконечно длинного соленоида. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной к его оси плоскости. Взятые попарно симметричные относительно такой плоскости витки создают поле, индукция которого перпендикулярна к плоскости (рис. 3.4.8). Следовательно, в любой точке внутри
и вне соленоида индукция может иметь лишь направление, параллельное оси.
Рис. 3.4.8
Возьмем прямоугольный контур 1–2–3–4–1 (рис. 3.4.9). Циркуляцию вектора B
по этому контуру можно представить следующим образом:
2
3
4
1
1
2
3
4
 Bl dl   Bl dl   Bl dl   Bl dl   Bl dl .
L
Из четырех интегралов, стоящих в правой части, второй и четвертый равны
нулю, так как B перпендикулярен к участкам контура, по которым они берутся.
Взяв участок 3–4 на большом расстоянии от соленоида, третьим слагаемым можно пренебречь (поле там заведомо очень слабое). Следовательно, из четырех сла2
гаемых остается одно:
 Bl dl   Bl dl  Bl
L
(здесь B – индукция поля в тех точках,
1
где располагается отрезок 1–2; l – длина этого отрезка). Контур 1–2–3–4–1 охватывает суммарный ток nlI , где n – число витков соленоида, приходящееся на
единицу его длины, I – сила тока в соленоиде. Используя теорему о циркуляции
B , получаем:  Bl dl  Bl  0nlI , откуда B  0 nI .
L
Рис. 3.4.9
Несложно доказать, что индукция поля, создаваемого тороидом, выражается
точно так же.
171
Пример 3. Из проволоки диаметром 1 мм необходимо намотать соленоид,
внутри которого напряженность магнитного поля должна быть равна 300 Э . Предельная сила тока, которую можно пропускать по проволоке, равна 6 А . Из какого числа слоев будет состоять обмотка соленоида, если витки наматывать плотно
друг к другу? Диаметр катушки считать малым по сравнению с ее длиной.
Решение.
По
условию
напряженность
магнитного
поля
H  nI  300 Э  24000 А м (1 Э  79,6 А м ). Здесь n – число витков на единицу
длины соленоида. Отсюда n  H I  4000 м1 . При диаметре проволоки
d  1 мм  0,001 м на длине 1 м уложится 1000 витков. Значит, обмотка соленоида будет содержать четыре слоя.
3.4.3. Намагничивание вещества
До сих пор мы говорили о магнитных полях, создаваемых проводниками с
током в вакууме. Если несущие ток проводники находятся в каком-либо веществе,
то магнитное поле существенным образом меняется. Это объясняется тем, что
всякое вещество является магнетиком, т. е. способно под действием магнитного
поля намагничиваться (приобретать магнитный момент) и создавать собственное
магнитное поле B , которое накладывается на магнитное поле, обусловленное токами, B0 . Результирующее поле определяется геометрической суммой B  B0  B .
В вакууме B  0 , отсюда B  B0  0 H .
Для объяснения намагничивания тел Ампер предположил, что в молекулах
вещества циркулируют круговые токи. Каждый такой ток создает в окружающем
пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи
ориентированы беспорядочным образом, вследствие чего их результирующее поле равно нулю. В силу этого же суммарный магнитный момент тела равен нулю.
Под действием внешнего поля магнитные моменты отдельных молекул приобретают преимущественную ориентацию в одном направлении; вследствие этого
магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля. Возникает магнитное поле B .
Намагничивание магнетика характеризуется магнитным моментом единицы
 Pm
объема. Эту величину называют вектором намагничивания: J  V
. Здесь V –
V
бесконечно малый объем; Pm – магнитный момент отдельной молекулы.
Чтобы понять, какое поле создается микротоками, рассмотрим магнетик в
форме бесконечного кругового цилиндра с сечением S в однородном внешнем
магнитном поле с индукцией B0 , параллельной оси цилиндра (рис. 3.4.10).
172
Рис. 3.4.10
Плоскости всех молекулярных токов расположатся перпендикулярно вектору B0 , так как магнитные моменты молекул Pm либо параллельны (для парамагнетиков), либо антипараллельны (для диамагнетиков) вектору B0 . Рассмотрим любое сечение цилиндра, перпендикулярное его оси. Во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг
другу, и их действие взаимно компенсируется. Не скомпенсированными будут
лишь молекулярные токи, выходящие на боковую поверхность цилиндра. Таким
образом, суммарное действие молекулярных токов будет таким, какое вызвал бы
макроскопический ток, текущий по поверхности цилиндра. Обозначим силу этого
тока, приходящуюся на единицу длины цилиндра (т. е. линейную плотность тока)
через I1 . Очевидно, что цилиндр, обтекаемый током, эквивалентен соленоиду с
числом ампер-витков nI , равным линейной плотности тока I1 . Следовательно, все
молекулярные токи совместно возбуждают такое поле, какое создал бы в вакууме
соленоид с числом ампер-витков, равным I1 . Напряженность поля в соленоиде
H  nI  I1 . Значит, магнитная индукция
B    0 H   0 I1 .
(*)
Выделим мысленно в цилиндре перпендикулярный к оси слой толщиной dl .
Молекулярные токи, заключенные в объеме этого слоя, эквивалентны круговому
току силы I1dl . Магнитный момент этого тока есть dPm  I1Sdl ( S – площадь поперечного сечения цилиндра). Разделив dPm на объем этого слоя dV  Sdl , полуdP I Sdl
 I1 . Из последнего
чим для намагничивания цилиндра выражение: J  m  1
dV
Sdl
выражения и из выражения (*) следует: В  0 J . (Учтено, что векторы B и J
имеют одинаковое направление.) Так как B  B0  B и B0  0 H ,
B  0 H  0 J  0 ( H  J ) . Как показывает опыт, вектор намагничивания связан с
напряженностью поля в той же точке соотношением J   H , где  – безразмерная величина, называемая магнитной восприимчивостью вещества. Используя
это, можно написать: B  0 1    H . Безразмерная величина 1     называется относительной магнитной проницаемостью вещества: B  0  H   B0 . Относительная магнитная проницаемость  показывает, во сколько раз усиливается
поле в магнетике.
173
Все магнетики подразделяются на три группы:
1. Диамагнетики – это магнетики, у которых магнитная восприимчивость
отрицательна и мала по величине (   0    1); в диамагнетиках создается поле,
направленное против внешнего поля и ослабляющее его; диамагнетиками являются Ag , Au, Cu и др.
2. Парамагнетики – это магнетики, у которых магнитная восприимчивость невелика, но положительна    0    1 ; поле, создаваемое в парамагнетиках имеет
то же направление, что и внешнее поле и усиливает его; при устранении внешнего поля парамагнетик размагничивается; парамагнетиками являются Pt , Al и др.
3. Ферромагнетики – это магнетики, у которых магнитная восприимчивость
положительна и достигает больших значений; они способны обладать намагничиванием даже в отсутствие внешнего магнитного поля; к их числу принадлежат
Fe, Ni, Co, Gd , их сплавы, соединения и ряд других веществ; намагничивание зависит от напряженности поля сложным образом.
3.4.4. Закон Ампера
Выше было сказано, что магнитное поле оказывает на контур с током ориентирующее действие. Следовательно, вращающий момент, испытываемый контуром с током, есть результат действия сил на отдельные элементы контура. Исследуя действие магнитного поля на различные проводники с током, Ампер установил, что сила, с которой магнитное поле действует на элемент проводника с током dl , прямо пропорциональна силе тока в проводнике и векторному произведению элемента с током и магнитной индукции: df  kI [dl B ] . Здесь k – коэффициент пропорциональности. Раскрывая векторное произведение, можно определить модуль этой силы: df  kIBdlSin (  – угол между направлениями поля и
элемента тока).
Направление силы, действующей на ток, удобно определять с помощью
правила левой руки. Если расположить левую руку так, чтобы вектор B «вонзался» в ладонь, а четыре сложенные вместе пальца были направлены вдоль тока, то
отставленный в сторону большой палец укажет направление силы.
Закон Ампера позволяет вычислить силу взаимодействия двух параллельных бесконечно длинных прямых токов (рис. 3.4.11). Если расстояние между токами b , то каждый элемент тока I 2 будет находиться в магнитном поле с индук I
цией B1  0 1 . Угол  между элементами тока I 2 и вектором B1 прямой (линии
2 b
магнитной индукции прямых токов – концентрические окружности, а вектор B
направлен по касательной). Следовательно, на единицу длины тока I 2 действует
 I I
сила f 21  kI 2 B1  k 0 1 2 . Для силы f12 , действующей на единицу длины тока
2 b
I1 , получается аналогичное выражение. Пользуясь правилом левой руки, легко
174
установить, что при одинаковом направлении токов они притягиваются, при различном – отталкиваются.
Рис. 3.4.11
В системе СИ коэффициент пропорциональности k равен единице  k  1 и
закон Ампера записывается в виде: df  I [dl B] , и модуль этой силы равен:
df  IBdlSin .
На основании закона Ампера устанавливается единица силы тока в СИ.
Единица силы тока в СИ – ампер – определяется как сила неизменяющегося тока,
который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу,
равную 2·10–7 Н на каждый метр длины.
Опираясь на закон Ампера, можно получить выражение для вращательного
момента, действующего на рамку с током в магнитном поле. Если прямоугольный
контур с током размещен в однородном магнитном поле ( B  const ) так, что его
плоскость и две стороны параллельны вектору индукции (рис. 3.4.12), то в соответствии с законом Ампера магнитное поле будет оказывать силовое воздействие только на стороны контура, перпендикулярные полю. При этом силы, действующие на
противоположные стороны, равны по величине ( f  f   IBa ) и противоположны по
направлению. Они образуют пару сил с моментом М  fb  IBab , ab  S – площадь
контура, а IS  Pm – магнитный момент контура. Отсюда M  Pm B .
Рис. 3.4.12
Вращательный момент стремится повернуть контур так, чтобы магнитный
момент Рт установился по направлению поля. В этом случае все стороны контура
окажутся перпендикулярны вектору В . По правилу левой руки легко определить,
175
что направления сил, действующих на все стороны контура, лежат в плоскости
контура. Эти силы в зависимости от направления тока в контуре будут либо сжимать контур, либо растягивать его.
Если контур ориентирован относительно поля произвольно, то вектор магнитной индукции В можно разложить на составляющие: перпендикулярную В и
параллельную ВII полю (рис. 3.4.13). Составляющая В будет растягивать или
сжимать контур. Составляющая ВII  BSin (  – угол между векторами Рт и В )
приведет к возникновению вращательного момента, равного M  Pm BII  Pm BSin .
Учитывая взаимную ориентацию векторов М , Рт , В , можно записать: М   Рт В  .
Рис. 3.4.13
Пример 4. Алюминиевый провод, площадь поперечного сечения которого
равна 1 мм 2 , подвешен в горизонтальной плоскости перпендикулярно магнитному меридиану, и по нему течет ток (с запада на восток) силой 1,6 А . Какую долю
от веса провода составляет сила, действующая на него со стороны земного магнитного поля? На сколько уменьшится вес 1 м вследствие этой силы? Горизонтальная составляющая напряженности земного магнитного поля равна 0,2 э .
Решение. В соответствии с законом Ампера сила, действующая в магнитном
поле на элемент проводника dl с током I равна dF  IBSin dl . Здесь B – индукция поля,  – угол между направлениями поля и тока. В нашем случае    2 .
Учитывая, что В  0  Н (  0 = 4  107 гн м – магнитная постоянная,  – магнитная проницаемость; для воздуха   1 ), для амперовой силы, действующей на
1 м провода, получаем:
F  1,6  4  3,14 107 1 0,2  79,6 1  3,2 105 H .
(Учтено, что 1 э  79,6 А м .) На эту величину уменьшится вес 1 м провода.
Вес 1 м алюминиевого провода сечением 1 мм 2 равен:
P  mg  lSg  2600  10 6  1  9.8  2.548  10 2 H  ,
где   2600 кг м3 – плотность алюминия ( см. приложение). Амперова сила составляет от веса провода:
F P  3, 2  105  2,548  102   0,126  102 .
176
3.4.5. Работа по перемещению проводника
с током в магнитном поле
Допустим, что проводник с током может свободно перемещаться во внешнем магнитном поле (например, с помощью скользящих контактов (рис. 3.4.14)).
Поле будем считать однородным и перпендикулярным к плоскости контура.
Рис. 3.4.14
Если известны направления тока и поля, то силу, действующую на подвижный проводник, вычислить несложно: f  IBl . На пути ds эта сила совершит над
проводником работу: dA  fds  IBlds . Вспоминая определение потока вектора
(«если имеется поле некоторого вектора A , то выражение Ф   An dS , где An – соS
ставляющая вектора A на направление нормали к dS , называется потоком вектора A через поверхность dS »), видим, что произведение Blds есть поток вектора
магнитной индукции через площадку lds . Поэтому dA  IdФ , где dФ – поток
магнитной индукции B , пересекаемый проводником при его движении.
Если поле неоднородное, то проводник нужно разбить на бесконечно малые
участки dl и сложить элементарные работы, совершаемые над каждым участком.
Если поле не перпендикулярно плоскости контура ( B составляет с нормалью к
контуру угол   0 ), то направление силы составит с направлением перемещения
также угол  (сила f перпендикулярна индукции B ) и dA  fCos ds  IBnlds , где
Bn  BCos – составляющая вектора B по направлению нормали к площадке lds ,
Bnlds  dФ – поток, пересекаемый проводником. Значит, и в этом случае dA  IdФ .
Найдем работу, совершаемую над замкнутым контуром с током при его перемещении в магнитном поле. Будем считать, что замкнутый контур, перемещаясь, остается все время в одной плоскости, перпендикулярной направлению поля
(рис. 3.4.15; В направлен за чертеж). Силы, приложенные к участку контура 1–2,
образуют с направлением перемещения острые углы; значит, работа этих сил А1
положительна. Участок 1–2 пересекает при своем движении поток Ф0 через заштрихованную поверхность и поток Фк , пронизывающий контур в его конечном
положении. Отсюда A1  I Ф0  Фк  .
177
Рис. 3.4.15
Силы, действующие на участок контура 2–1, образуют с направлением перемещения тупые углы, поэтому совершаемая ими работа отрицательна. Абсолютная величина ее пропорциональна сумме потоков Ф0 и Фн – потока пронизывающего контур в начальном положении: A2   I Ф0  Фн  . Полная работа над контуром равна
A  A1  A2  I Ф0  Фк   I Ф0  Фн    I Фк  Фн   I Ф ,
где Ф – изменение потока через контур.
Пример 5. Два прямолинейных длинных параллельных проводника находятся
на расстоянии 10 см друг от друга. По проводникам текут токи в одном направлении
I1  20 A и I 2  30 A . Какую работу надо совершить (на единицу длины проводников), чтобы раздвинуть эти проводники до расстояния 20 см ?
x2
Решение. Искомая работа выразится интегралом A  Fdx . Здесь F – сила
x1
взаимодействия проводников; x – расстояние между проводниками. По закону
Ампера сила взаимодействия параллельных проводников с током равна:
 I I l
F  0 1 2 . Здесь  0 – магнитная постоянная,   1 – магнитная проницаемость
2 d
воздуха, l – длина проводника, d – расстояние между проводниками. Расстояние
между проводниками меняется. Отсюда
0  I1I 2l
 I I l x
dx  0 1 2 n 2 .
2 x
2
x1
x1
x2
A 
Подставляя данные задачи, получаем: A l  8,31105  Дж м  .
3.4.6. Сила Лоренца
Проводник, по которому течет ток, отличается от проводника без тока лишь
тем, что в нем происходит упорядоченное движение зарядов. Отсюда вывод, что
сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, а уж от них действие передается
проводнику, по которому они перемещаются. Тот факт, что заряженные частицы
отклоняются магнитным полем, подтверждается целым рядом опытных фактов,
например, отклонением пучка электронов в электронно-лучевой трубке.
178
Согласно закону Ампера на элемент, тока dl в магнитном поле действует сила
df  I [dl B ] . Вводя в рассмотрение плотность тока, можно написать: I  jS . Вектор
плотности тока j и вектор dl направлены одинаково. Используя это, получим:
d f  I [dl B ]  [ Idl B ]  [ SdljB ]  Sdl[ jB ] .
Если в единице объема проводника содержится n носителей заряда с величиной заряда e каждый, двигающихся со средней скоростью v , то за единицу
времени через единичную площадку будет перенесен заряд env , т. е. плотность
тока можно записать следующим образом: j  env . (Следует отметить, что когда
заряды положительны, векторы j и v направлены одинаково; если заряды отрицательны – эти векторы направлены противоположно.)
Подставим последнее выражение для плотности тока в закон Ампера:
d f  Sdlen uB  . Произведение nSdl есть число зарядов в элементе проводника
длиной dl . Разделив выражение для силы на это произведение, получим силу,
действующую на один заряд: f  e vB  . Эту силу называют силой Лоренца.
Модуль лоренцевой силы равен: f  evBSin , где  – угол между векторами v и B . Отсюда видно, что заряд, движущийся вдоль направления магнитного
поля, не испытывает действия силы.
Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат
векторы v и B . Для определения направления лоренцевой силы можно пользоваться правилом левой руки. Если расположить левую руку так, чтобы вектор В
вонзался в ладонь, а четыре сложенных пальца были направлены вдоль вектора v ,
то отставленный большой палец укажет направление силы, действующей на положительный заряд. В случае, когда заряд отрицателен, найденное таким способом направление силы нужно изменить на обратное.
С помощью силы Лоренца можно объяснить возникновение разности потенциалов между концами проводника, пересекающего линии магнитного поля
(рис. 3.4.16). При движении проводника относительно магнитного поля со скоростью v с той же скоростью будут перемещаться относительно поля и носители заряда. При этом на каждый носитель будет действовать сила f  evB (предполагается, что поле, проводник и направление его движения взаимно перпендикулярны).
Под действием этой силы положительные заряды станут перемещаться к
концу проводника, обозначенному знаком «+» (отрицательные перемещались бы
в противоположную сторону). В результате возникнет направленное вдоль проводника электрическое поле напряженности Е , которое будет препятствовать перемещению зарядов, вызванному силой Лоренца. Когда напряженность поля Е
достигнет в каждой точке такой величины, что сила f E  eE уравновесит силу
Лоренца, перераспределение зарядов вдоль проводника прекратится и наступит
равновесное состояние. Отвечающее этому состоянию значение Е можно найти
из условия eE  evB , где E  vB .
179
Рис. 3.4.16
Умножив напряженность электрического поля на длину проводника l , получим
напряжение между концами проводника: U  1  2  El  Bvl . Произведение Bvl
равно потоку Ф вектора В , пересекаемому проводником за одну секунду. Таким
образом, U  dФ dt .
Если концы движущегося в магнитном поле проводника заставить скользить по замыкающему их неподвижному проводнику, в образовавшейся замкнутой цепи потечет ток. Величина э. д. с., действующей в цепи, будет определяться
выражением для U .
Сила Лоренца всегда перпендикулярна к скорости заряженной частицы.
Представим себе заряд е , влетающий в однородное магнитное поле со скоростью
v  B . Под действием силы Лоренца заряд приобретает постоянное по величине
f e
нормальное ускорение: wn   vB (угол между векторами v и B прямой).
m m
Если скорость изменяется только по направлению, движение с постоянным по величине нормальным ускорением представляет собой равномерное движение по
окружности, радиус которой определяется из условия wn  v 2 R . Имеем:
e
v 2 e
mv
. Отношение
называется удельным зарядом.
 vB  R 
m
R m
e B
Период обращения заряда по окружности находится делением длины
m1
окружности 2 R на скорость v : T  2
. Период обращения заряженной чаe B
стицы по окружности оказывается не зависящим от ее скорости, он определяется
только удельным зарядом частицы и магнитной индукцией поля.
Пример 6. Прямой проводник длиной l  1 м перемещается в магнитном
поле, при этом проводник, магнитное поле и направление перемещения перпендикулярны между собой. Определить силу Лоренца, с которой магнитное поле
действует на свободный электрон, находящийся в проводнике, если возникающая
на его концах разность потенциалов U  3  105 B .
Решение. Сила Лоренца равна Fл  evBSin . Здесь e – заряд электрона, v –
его скорость, B –- индукция магнитного поля,  – угол между направлениями
поля и скорости. По условию    2 . Поскольку напряжение между концами
проводника, пересекающего магнитное поле, равно U  Bvl , то Bv  U l . Учитывая это, для лоренцевой силы, получаем: F  e U l   4,8 1024  H  .
180
3.5. Электромагнитная индукция
3.5.1. Опыты М. Фарадея. Закон Фарадея
Мы уже знаем, что электрические токи создают вокруг себя магнитные поля. Открытое английским физиком М. Фарадеем явление электромагнитной индукции состоит в том, что в замкнутом проводнике при изменении потока магнитной индукции через поверхность, ограниченную этим проводником, возникает
электрический ток. Таким образом, возможно и обратное явление: магнитные поля создают электрический ток, который называется индукционным.
Величина индукционного тока не зависит от способа, которым вызывается
изменение потока магнитной индукции, и определяется лишь скоростью изменения магнитного потока.
Этот результат был установлен М. Фарадеем в его классических опытах по
обнаружению электромагнитной индукции. М. Фарадей вдвигал в катушку провода, соединенную с гальванометром (или выдвигал из нее) постоянный магнит
или другую катушку меньшего диаметра, питаемую от батареи постоянного тока
(рис. 3.5.1). Каждый раз при движении магнита (или катушки) гальванометр обнаруживал в цепи ток. При смене направления движения магнита (или катушки) ток
менял направление.
Рис. 3.5.1
Ленц установил правило, с помощью которого можно найти направление
индукционного тока. Это правило гласит: индукционный ток всегда направлен
так, чтобы противодействовать причине, его вызывающей. Действительно, если
создавать магнитное поле контуром, соединенным с батареей постоянного тока, и
двигать в этом поле второй контур, соединенный с гальванометром (рис. 3.5.2), то
во втором контуре возникнет индукционный ток такого направления, что сила,
действующая на него, будет противиться движению контура.
181
Рис. 3.5.2
При приближении контура 2 к первому, в нем возникает индукционный ток
i2 , магнитный момент которого направлен против внешнего поля (угол  между
векторами Pm и B равен  ), и на контур 2 будет действовать сила, отталкивающая его от первого контура. При удалении контура 2 от первого контура возникнет ток i2 , момент которого Pm совпадает по направлению с B (   0 ), так что
сила, действующая на контур 2, имеет направление к контуру 1.
Если контур 2 неподвижен, и ток индуцируется в нем путем изменения тока
i1 в первом контуре, то во втором контуре индуцируется ток i2 такого направления, что создаваемый им собственный магнитный поток будет стремиться ослабить изменения внешнего потока, которые приводят к появлению индукционного
тока. При увеличении i1 , т. е. при возрастании внешнего магнитного потока,
направленного вправо, возникнет ток i2 , создающий поток, направленный влево.
При уменьшении i1 возникнет ток i2 , собственный магнитный поток которого
направлен так же, как и внешний поток и, следовательно, стремится поддержать
внешний поток неизменным.
Мы уже знаем, что если в цепи течет ток, то в этой цепи присутствует э. д. с.
Если в контуре возник индукционный ток, значит, изменение потока Ф магнитной индукции через контур приводит к возникновению в нем э. д. с. индукции  i .
Используя закон сохранения энергии, установим связь э. д. с. индукции  i со скоростью изменения магнитного потока dФ dt . Рассмотрим контур в однородном
магнитном поле (рис. 3.5.3).
Рис. 3.5.3
182
Пусть в контуре действует э. д. с.  , которая создает ток I . Работа источника тока за время dt , как известно, равна dA   Idt . (Здесь учтено, что для замкнутой цепи работа электростатических сил равна нулю: A   q  1  2  q; 1  2 .)
Будем считать, что участок 1–1 может перемещаться без нарушения контакта с
остальной цепью. Когда этот участок неподвижен, вся работа dA превращается в
джоулево тепло: dQ  RI 2dt . Если участку 1–1 дать возможность перемещаться,
то за время dt он перейдет в положение 2–2. Амперова сила при этом совершит
работу dA  IdФ . ( f  IBl  dA  fds  IВlds  IdФ , так как lds  dS и
BdS  dФ .) Здесь dФ – приращение магнитного потока. Эта работа также совершается за счет источника тока, так как внешнее магнитное поле при этом не меняется. Значит, работа источника тока затрачивается на джоулево тепло и работу по пе  dФ dt
ремещению участка проводника  Idt  RI 2dt  IdФ . Отсюда I 
. Как изR
вестно, по закону Ома для замкнутой цепи I   R . Из полученного же выражения
следует, что при изменении магнитного потока через контур сила тока в нем оказывается такой, как если бы кроме э. д. с. источника  в контуре действовала бы э. д. с.,
равная  dФ dt . Очевидно, что это и есть э. д. с. индукции i . Таким образом,
i   dФ dt . Знак минус показывает, что увеличение потока ( dФ dt  0 ) вызывает
э. д. с. i  0 , т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока ( dФ dt  0 ) вызывает i  0 , т. е. направления потока и поля индукционного тока совпадают. Таким образом, знак минус в формуле для э. д. с. индукции
является математическим выражением правила Ленца. Сама же формула выражает закон, установленный Фарадеем: «Какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с. i   dФ dt ».
Единицей потока магнитной индукции в системе СИ служит вебер ( Вб ), который представляет собой поток через поверхность 1 м 2 , пересекаемую нормальными к ней линиями магнитного поля с индукцией В , равной 1Тл . При скорости
изменения потока, равной 1 Вб с , в контуре индуцируется э. д. с., равная 1 В .
Если контур, в котором индуцируется э. д. с., состоит из N одинаковых
витков, соединенных последовательно, т. е. представляет собой соленоид, то суммарная э.д.с. будет равна сумме э. д. с., индуцируемых в каждом витке:
N
 dФ j 
d
i   
     Ф  . Величина   Ф называется полным магнитным
dt
j 1  dt 
потоком или потокосцеплением. Если поток через каждый виток одинаков, то
  NФ . Таким образом, для соленоида i   d dt .
Пример 1. В однородном магнитном поле, индукция которого В  0,5 Тл ,
равномерно с частотой 300 мин1 , вращается катушка, содержащая N  200 витков, плотно прилегающих друг к другу. Площадь поперечного сечения катушки
183
S0  100 см2 . Ось вращения перпендикулярна оси катушки. Определить максимальную э. д. с., индуцируемую в катушке.
Решение. Катушка представляет собой соленоид, для которого i   d dt ,
где   NФ – потокосцепление. Магнитный поток Ф  ВS , где S – площадь сечения катушки в проекции на плоскость, перпендикулярную направлению поля:
S  S0Cos (  – угол между нормалью к площади сечения катушки и направлением поля). Отсюда i  NBS0 Sin  d dt  . Скорость изменения угла  по усло-
вию равна 300 мин1  5 с 1  10 рад с . Максимальное значение э. д. с. imax будет
достигнуто, когда Sin  1 . Таким образом, imax  NBS0  d dt   31, 4  B  .
Пример 2. Однородное магнитное время нарастает пропорционально времени: В  kt , где k  10 Тл с . Какое количество теплоты выделится в рамке,
имеющей форму квадрата со стороной а  1 м за время t2  t1  2 c ? Рамка сделана
из алюминиевого провода с поперечным сечением S  1 мм2 . Плоскость рамки
расположена перпендикулярно полю. Температура в помещении равна 20 С .
Решение. По условию В  kt . Поскольку магнитный поток Ф  BS , то
i   dФ dt  


d
kta 2  ka 2 . В рамке действует только э. д. с. индукции. Значит,
dt
по закону Джоуля–Ленца выделившееся тепло равно:
Q  i2 R   t2  t1    k 2a 4  l   S  t2  t1  .
Здесь R  l S – сопротивление рамки. Подставив данные задачи, получим:
Q  1,72 103  Дж  .
3.5.2. Токи Фуко
Индукционные токи могут возбуждаться и в сплошных массивных проводниках. Такие токи называются токами Фуко. Сопротивление массивных проводников малό, из чего следует, что токи Фуко могут достигать очень большой силы.
Как и любой индукционный ток, токи Фуко подчиняются правилу Ленца:
внутри проводника они выбирают такие направления, чтобы своим действием
возможно сильнее противиться причине, которая их вызвала. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это обстоятельство используется для демпфирования (успокоения) подвижных частей
гальванометров, сейсмографов и других приборов. На подвижной части прибора
укрепляется хорошо проводящая пластина в виде сектора, которая вводится между полюсами сильного постоянного магнита (рис. 3.5.4). При движении пластины
в ней возникают вихревые токи (токи Фуко), вызывающие торможение системы.
Преимущество такой системы состоит в том, что торможение возникает
лишь при движении пластинки и отсутствует, когда пластинка неподвижна. Поэтому электромагнитный успокоитель не препятствует точному приходу системы
в положение равновесия.
184
Рис. 3.5.4
В кусках металла достаточно толстых, т. е. имеющих большие размеры в
направлении индуцированного тока, вихревые токи вследствие малости сопротивления могут быть очень большими и вызвать очень значительное нагревание. Если,
например, поместить внутрь катушки массивный металлический сердечник и пропустить по катушке переменный ток частотой 100 гц , то сердечник сильно разогреется.
Тепловое действие токов Фуко используется в индукционных печах, представляющих собой катушку, питаемую высокочастотным током большой силы.
Если поместить внутрь катушки проводящее тело, то в нем возникнут интенсивные вихревые токи, которые могут разогреть тело до плавления. Таким способом
осуществляют плавление металлов в вакууме, что позволяет получать материалы
исключительно высокой чистоты.
Для предотвращения потерь энергии на нагревание токами Фуко сердечников
трансформаторов, последние раньше набирались из тонких пластин, разделенных
изолирующими прослойками, для увеличения сопротивления токам Фуко. С появлением магнитных материалов с большим электрическим сопротивлением (так называемых, ферритов) сердечники трансформаторов стали делать сплошными.
3.5.3. Явление самоиндукции
Вернемся теперь к опытам Фарадея по обнаружению электромагнитной индукции (рис. 3.5.5). Катушка 1, питаемая от батареи, вставлялась внутрь катушки 2, при
этом катушка 1 создавала внутри катушки 2 магнитный поток. При всяком изменении
этого потока в катушке 2 возникал индуцированный ток. Индуцированный ток возникает во всяком контуре, через который магнитный поток меняется.
Но ведь и сама катушка 1 находится в таком же положении. Сквозь ее витки
также проходит магнитный поток, обусловленный магнитным полем самой катушки. Поэтому при всяком изменении магнитного поля, создаваемого током в
этой катушке, т. е. при всяком изменении тока в катушке, в ней самой должны
возникнуть и индуцированная э. д. с. и индуцированный электрический ток. Индукцию в этом случае принято называть самоиндукцией.
185
Рис. 3.5.5
Обнаружить на опыте самоиндукцию несложно. Возьмем катушку J с несколькими сотнями витков, надетую на замкнутый железный сердечник
(рис. 3.5.6). К зажимам катушки а–а присоединим шестивольтовую лампочку L.
Катушку можно с помощью ключа К присоединить к аккумулятору с напряжением 1,5  2,0 В. Когда ключ К замкнут, к аккумулятору присоединены параллельно
катушка и лампочка. Если ключ К разомкнут, то мы имеем только одну замкнутую цепь, состоящую из катушки и лампочки.
Рис. 3.5.6
Пока ключ замкнут, лампочка горит слабо (она рассчитана на 6 В). В момент размыкания ключа лампочка вспыхивает очень ярким белым светом. Почему? После размыкания ключа ток в катушке уменьшается, т. е. магнитное поле
ослабевает. Вследствие самоиндукции создается кратковременная, но довольно
значительная э.д.с., под действием которой через катушку и лампочку протекает в
течение очень короткого времени большой ток, заставляющий лампочку ярко
вспыхнуть.
186
3.5.4. Токи при размыкании и замыкании цепи
По правилу Ленца дополнительные токи, возникающие в проводниках
вследствие самоиндукции, всегда направлены так, чтобы препятствовать изменениям тока, текущего в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а
постепенно.
Пусть в цепь с не зависящей от тока индуктивностью L и сопротивлением
R включен источник тока с э. д. с.  (рис. 3.5.7).
Рис. 3.5.7
Под действием э. д. с. в цепи будет течь ток I 0   R (сопротивления источника и катушки считаем малыми). В момент времени t0 отключим источник тока,
замкнув одновременно цепь накоротко переключателем К. Как только сила тока в
цепи начнет убывать, возникнет э. д. с. самоиндукции  s , которая приведет к паR
 t
L
дению тока в цепи по экспоненциальному закону: i  I 0e . Действительно, по
закону Ома iR   s ; так как
d  Li 
d
dL 
di
 di
s  

   L  i   L ,
dt
dt
dt 
dt
 dt
di
di R
di
R
R
  i  0    dt  ln i   t  ln C
dt
dt L
i
L
L
При t  0 имеем i  I 0  C  I 0 , где I 0 – ток в цепи в установившемся режиме. Потенцируя, получаем выше приведенную зависимость тока от времени.
Скорость убывания тока определяется имеющей размерность времени величиной
iR   L

t
  L R , называемой постоянной времени. Таким образом, i  I 0e . В соответствии с этой записью  есть время, в течение которого сила тока уменьшается в e
раз. Чем больше индуктивность L и чем меньше сопротивление R , тем больше
постоянная времени  и тем медленнее спадает ток в цепи.
В случае замыкания цепи (т. е. подключения к источнику тока) до тех пор,
пока сила тока не примет установившегося значения I 0 , в цепи, кроме э. д. с.  ,
будет действовать э. д. с. самоиндукции  s , которая приведет к тому, что ток в
187

цепи
будет
нарастать
по
закону
R
 t

i  I 0 1  e L  .


Действительно,
di
di R 
  i .
dt
dt L
L
По сравнению с предыдущим случаем в правой части появился член, отличный от нуля. Общее решение неоднородного дифференциального уравнения равно общему решению однородного уравнения плюс частное решение неоднородного уравнения. Общее решение однородного уравнения было получено выше;
частное решение неоднородного уравнения очевидно: i  I 0   R . Сумма этих
iR     s    L
R
 t
L
решений ( i  I 0  C  e ; C – постоянная) дает закон нарастания силы тока в цепи. Действительно, в начальный момент времени i  0 , откуда C   I 0 . Значит,
R
 t

i  I 0 1  e L  .


График убывания и нарастания силы тока при размыкании и замыкании цепи представлен на рис. 3.5.8.
Рис. 3.5.8
Пример 3. Определить, через какое время сила тока замыкания достигнет
0,98 предельного значения, если источник тока замыкают на катушку сопротивлением 10 Ом и индуктивностью 0,4 Гн .
R
R
R
 t
 t
 t

L
L
Решение. i  I 0 1  e   I 0  i  e . Поскольку i  0,98 I 0 , то 0,02  e L .


Логарифмируя последнее равенство, получаем:
n0, 02  
R
t  t  0,156  c  .
L
3.5.5. Индуктивность
В соответствии с законом Био–Савара–Лапласа индукция магнитного поля
пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток в катушке i и создаваемый им полный магнитный поток  пропорциональны друг другу:
  Li . Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура.
188
Необходимо отметить, что линейная зависимость полного магнитного потока  от силы тока i имеет место лишь в том случае, если относительная магнитная проницаемость  среды, которой окружена катушка, не зависит от напряженности поля H , т. е. при отсутствии ферромагнетиков.
Индуктивность катушки (или любого другого контура) зависит от ее геометрии (т. е. от формы и размеров) и магнитных свойств окружающей среды. За
единицу индуктивности принимается индуктивность такого проводника, у которого при силе тока в нем 1 А возникает полный магнитный поток, равный 1 Вб .
Эту единицу называют генри ( Гн ).
Вычислим индуктивность бесконечного соленоида. Магнитная индукция
поля внутри соленоида равна: B  0  H  0  ni , где n – число витков на единицу длины. Поток магнитной индукции через каждый из витков Ф  BS , а полный
магнитный поток (потокосцепление)   NФ  nlBS  0  n2lSi ( l – очень большая
длина соленоида; S – площадь поперечного сечения). Так как   Li , то
N2
2
S.
L  0  n lS или L  0 
l
Пример 4. Обмотка соленоида состоит из N витков медной проволоки, поперечное сечение которой S  1 мм2 . Длина соленоида l  25 см и его сопротивление R  0, 2 Ом . Найти индуктивность соленоида.
N2
Решение. Индуктивность соленоида L  0 
S , где S – площадь витка
l
соленоида. Для нахождения площади витка имеем: длина окружности витка
С  l1 N ( l1 – длина проволоки); l1  Rs  , где  – удельное сопротивление меди.
Поскольку С  2 r , то r  l1  2 N   Rs  2 N  . Отсюда площадь витка равна:
R2s2
S r 
. Подставляя это выражение в формулу для L , получаем:
4 2 N 2
2
L
0  R 2 s 2
 5,5 105  Гн  . Учтено, что для воздуха   1 .
2
4 l 
3.5.6. Энергия магнитного поля
Вернемся к схеме, изображенной на рис. 3.5.7. Если катушка (соленоид) L замкнута на батарею  , то в ней устанавливается ток I 0 , который обусловливает магнитное поле, сцепленное с витками. Если отключить соленоид от батареи, замкнув его
на сопротивление R , то в образовавшейся цепи будет некоторое время течь постепенно убывающий ток. Работа, совершаемая этим током, за время dt , равна
d
dA   sidt  
idt  id . Если индуктивность постоянна ( L  const ), то d  Ldi ,
dt
и выражение для работы принимает следующий вид: dA   Lidi . Интегрирование этого выражения по i от первоначального значения i до нуля позволяет получить работу, совершаемую в цепи за время исчезновения тока и, соответственно, магнитного
189
0
Li 2
поля: A    Lidi 
. Эта работа идет на приращение внутренней энергии провод2
i
ника, т. е. на его нагревание. Совершение этой работы сопровождается исчезновением
магнитного поля. Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа. Значит, проводник с индукLi 2
тивностью L , по которому течет ток i , обладает энергией W 
, которая локали2
зована в возбуждаемом током магнитном поле.
Вычислим энергию магнитного поля соленоида. Поскольку индуктивность
N 2S
0  N 2 I 2
соленоида L  0 
, то W 
S . Так как ток, текущий в соленоиде,
l
2
l
связан с характеристиками соленоида и поля внутри него соотношением
I  Н n  Bl  0  N  и B  0  H , то W  B 2V  20    BHV 2 .
3.5.7. Взаимная индукция
Выясним теперь, как влияют друг на друга два контура с током, двигающиеся
друг относительно друга, либо меняющие магнитный поток изменением тока.
Рассмотрим два контура 1 и 2, расположенных друг относительно друга не
очень далеко (рис. 3.5.9).
Рис. 3.5.9
Если в первом контуре течет ток силы i1 , он создаст через другой контур
пропорциональный i1 полный магнитный поток  2  L21i1 (поле этого потока
изображено сплошными линиями). При изменении i1 во втором контуре индуциdi
руется э. д. с. i 2  L21 1 , аналогично, при протекании во втором контуре тока сиdt
лы i2 возникает связанный с первым контуром полный магнитный поток  1  L12i2
(поле этого потока изображено пунктирными линиями). При изменении тока i2 в
di
контуре индуцируется э. д. с. i1   L12 2 . Контуры 1 и 2 называются связанныdt
ми, а явление возникновения э. д. с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности
L21 и L12 называются взаимной индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что L12  L21 . Взаимная индуктивность зависит от
190
формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающей контуры среды. Взаимная индуктивность измеряется в
тех же единицах, что и индуктивность, т. е. в генри.
Рассчитаем взаимную индуктивность двух катушек, намотанных на общий
тороидальный железный сердечник. Этот случай имеет большое практическое
значение, так как на один сердечник, как правило, наматывается несколько катушек. Линии магнитной индукции в этом случае сосредотачиваются внутри сердечника и можно считать, что возбуждаемое любой из обмоток магнитное поле
будет иметь всюду в сердечнике одинаковую индукцию. Если первая обмотка
имеет N1 витков и по ней течет ток силой i1 , то для магнитной индукции поля
N
внутри тороида, создаваемого этой катушкой, можно написать B  0  1 i1 ( l –
l
длина сердечника). Поток магнитной индукции через поперечное сечение сердечN
ника Ф  BS  0  1 i1 , где S – площадь поперечного сечения сердечника.
l
Умножая на N 2 , получим полный поток магнитной индукции, сцепленный со
S
S
второй обмоткой  2  0  N1 N 2i1 . Так как  2  L21i1 , то L21  0  N1N 2 .
l
l
Вычислив поток  1 , связанный с первой обмоткой в предположении, что во
второй обмотке течет ток силой i2 , найдем, что взаимная индуктивность L12 имеет
точно такое же выражение, как и L21 .
Пример 5. Два соленоида (индуктивность одного L1  0,36 Гн , второго
L2  0,64 Гн ) одинаковой длины и практически равного сечения вставлены один в
другой. Определить взаимную индуктивность соленоидов.
S
Решение. L21  0  N1 N 2 – взаимная индукция двух соленоидов. Индукl
N2
тивность каждого соленоида дается выражением: L  0 
S , где N – число
l
витков соленоида, l – его длина, S – площадь поперечного сечения. Отсюда для
L1l
L2l
; N2 
числа витков каждого соленоида имеем: N1 
. Подставляя
0  S
0  S
эти выражения в L12 , получаем: L12  L1L2  0,36  0,64  0,48 Гн .
На явлении взаимной индукции основан принцип действия трансформаторов (рис. 3.5.10), применяемых для повышения или понижения напряжения переменного тока. Первичная и вторичная катушки, имеющие, соответственно, N1 и
N 2 витков, намотаны на замкнутый железный сердечник. Концы первой обмотки
подсоединены к источнику переменного напряжения с э. д. с. 1 , возбуждающей
переменный ток I1 . Этот ток возбуждает в сердечнике трансформатора переменный магнитный поток, пронизывающий обе катушки. При этом во второй катушке появляется э. д. с. взаимной индукции, а в первой – э. д. с. самоиндукции.
191
Рис. 3.5.10
По закону Ома падение напряжения в первой катушке равно разности э. д. с.
источника и э. д. с. самоиндукции: I1R1  1  d  N1Ф  dt , где R1 – сопротивление
dФ
первой катушки. В силу малости сопротивления R1 имеем: 1  N1
.
dt
Э. д. с., возбуждаемая во второй обмотке:  2   N 2 dФ dt . Из сравнения выN
ражений для 1 и  2 получаем:  2   2 1 . ( Знак минус указывает, что э. д. с. в
N1
катушках противоположны по фазе). Отношение N 2 N1 называется коэффициентом трансформации. Если N 2 N1  1 – трансформатор повышающий (повышает
э. д. с. и понижает ток). Если N 2 N1  1 – трансформатор понижающий (понижает
э. д. с. и повышает ток).
Пример 6. Трансформатор, понижающий напряжение с U  5,5 кВ до
U 2  220 B , содержит в первичной обмотке N1  1500 витков. Сопротивление вторичной обмотки R2  2 Ом . Сопротивление внешней цепи (в сети пониженного
напряжения) R  13 Ом . Пренебрегая сопротивлением первичной обмотки, определить число витков во вторичной обмотке трансформатора.
Решение. Во внешней цепи пониженного напряжения падение напряжения
составляет U 2  220 B . Значит, в цепи течет ток I 2  220 13  16,92  A . Отсюда, падение напряжения во всей вторичной цепи, равное индуцированной э. д. с., составит 2  I 2  R1  R   253,8  B  . При условии пренебрежения сопротивлением первичной катушки 1  U1 . Так как для трансформатора  2 1  N 2 N1 , то
N
N 2  2 1  69 витков.
1
3.5.8. Переменный ток
Опыт показывает, что закон Ома и правила Кирхгофа, установленные для
постоянного тока, справедливы и для изменяющихся токов, если только изменения происходят не слишком быстро. Электромагнитные возмущения распространяются по цепи со скоростью света с . Если за время   l c , необходимое для передачи возмущения в самую отдаленную точку цепи, сила тока изменяется незначительно, то можно пренебречь этими изменениями и считать силу тока постоянной в течение этого времени. Для периодически изменяющихся токов это условие
192
запишется в виде   l c  T , где T – период изменений. Ток промышленной частоты (  50 Гц ) удовлетворяет этому для цепей длиной 100 км .
Пусть к зажимам сопротивления R , не обладающего индуктивностью и емкостью (т. е. активного сопротивления) (рис. 3.5.11 а), приложено напряжение,
изменяющееся по закону U  U mCost ( U m – амплитудное значение напряжения).
U U
По закону Ома i   m Cost  I mCost , т. е. между амплитудными значенияR R
ми силы тока и напряжения имеется соотношение: I m  U m R .
Соотношения между переменными токами и напряжениями очень удобно
изображать с помощью векторной диаграммы. Выберем произвольное направление, которое назовем осью токов (рис. 3.5.11 б). Отложим вдоль этого направления вектор длиной I m . В нашем случае ток и напряжение изменяются синфазно,
поэтому вектор напряжения тоже будет направлен вдоль оси токов, и длина его
будет равна RI m . Совокупность этих двух векторов и будет представлять векторную диаграмму нашей цепи.
Рис. 3.5.11
Если подать напряжение, изменяющееся по закону U  U mCost на концы
индуктивности L  const с пренебрежимо малыми сопротивлением и емкостью
(рис. 3.5.12 а), то в индуктивности будет течь переменный ток, и возникнет э. д. с.
di
самоиндукции  s   L . Закон Ома для индуктивности (т. е. для неоднородного
dt
участка) запишется в виде:
di
U mCost  L  0 .
dt
(Действительно, iR  1  2  12 ; 1  2  U  U mCost; 12   s ). Отсюда
di
L  U mCost .
dt
Разделяя
переменные
и
производя
интегрирование,
получаем:
U
i  m Sint  const . Ток переменный, постоянной составляющей нет, значит,
L
U

U
const  0 и i  m Sint  I mCos (t  ) , где I m  m . Из последнего соотношеL
2
L
ния видно, что роль сопротивления играет величина X L   L , называемая реак193
тивным индуктивным сопротивлением. Если индуктивность измерять в генри,
частоту – в герцах, то X L будет выражено в омах.
Из выражения X L   L видно, что индуктивное сопротивление растет с
увеличением частоты. Постоянному току (   0 ) индуктивность не оказывает сопротивления.
Поскольку в нашей цепи R  0; C  0 , то все напряжение приложено к индуктивности; значит падение напряжения на индуктивности равно:
U L  U mCost   LI mCost . Сравнивая это выражение с выражением для тока,
видим, что падение напряжения на индуктивности опережает по фазе ток, текущий через индуктивность на  2 . Если ось токов направить горизонтально, то
векторная диаграмма для этой цепи будет иметь вид, как на рис. 3.5.12 б.
Рис.3.5.12
Рассмотрим теперь случай, когда периодически меняющееся напряжение
подано на емкость С (рис. 3.5.13 а). Индуктивное и активное сопротивления полагаем равными нулю. Емкость непрерывно перезаряжается, вследствие чего в
цепи течет переменный ток. Напряжение на конденсаторе U С  q C можно считать равным внешнему напряжению U :
U С  q C  U mCost .
Отсюда i  dq dt  CU m Sint  I mCos t   2  .
U
Здесь I m  СU m  m . Как видно, роль сопротивления играет в этом слу1
C
чае величина X C  1
C , называемая реактивным емкостным сопротивлением. Если
емкость измерять в фарадах, частоту – в герцах, то X C будет выражено в омах.
Для постоянного тока   0  X C   . Отсюда следует, что постоянный ток
через конденсатор течь не может. Переменный ток   0  может течь через конденсатор, причем сопротивление току будет тем меньше, чем больше частота и емкость.
Заменяя в выражении для падения напряжения на емкости U m через I m , по1
I Cost . Сравнивая это с выражением для тока через емкость,
лучим: U C 
C m
видим, что падение напряжения отстает по фазе от тока на  2 , и векторная диаграмма для нашего случая выглядит, как на рис. 3.5.13 б.
194
Рис.3.5.13
Объединим теперь все три случая и рассмотрим цепь, составленную из активного сопротивления R , индуктивности L и емкости C (рис. 3.5.14 а). Подадим на
концы этой цепи переменное напряжение U  U mCost . В цепи возникнет переменный ток частоты  . Амплитуда и фаза тока, очевидно, определяются параметрами
цепи R, L, C. Этот ток вызовет на активном сопротивлении падение напряжения U R ,
амплитуда которого равна RI m , а фаза совпадает с фазой тока. Поэтому на векторной
диаграмме (рис. 3.5.14 б) вектор, изображающий U R , нужно отложить по оси токов.
Падение напряжения на индуктивности U L с амплитудой  LI m опережает ток по фазе на  2 , поэтому вектор, изображающий U L , должен быть повернут относительно
оси токов на угол  2 против часовой стрелки. Падение напряжения на емкости U C ,
1
I , отстает от тока по фазе на  2 , следовательно, вектор,
имеющее амплитуду
C m
изображающий U C , должен быть повернут относительно оси токов на угол  2 по
часовой стрелке. Сумма падений напряжений U R ,U L ,U C должна быть равна приложенному к цепи напряжению U . Поэтому, сложив векторы, изображающие
U R ,U L ,U C , мы получим вектор, изображающий U . Этот вектор образует с осью то L  1C
ков угол  , тангенс которого равен tg 
. Угол  задает разность фаз
R
между напряжением U и силой тока i . Из прямоугольного треугольника, гипотенуза
которого
Im 
Um ,

следует:
Um
R  L  1
2
C

2
 RI m 
2


2
2

  L  1
C I m   U m ,

откуда
. Таким образом, если напряжение на зажимах цепи изменя-
ется по закону U  U mCost , то в цепи течет ток i  I mCos t    .
φ
Рис. 3.5.14
195

C 
Величина Z  R 2   L  1
2
 R2   X L  X C 
2
называется полным
сопротивлением цепи. Величина X  X L  X C   L  1
C называется реактив-
ным сопротивлением. Таким образом, Z  R 2  X 2 . Ток отстает от напряжения
  0 или опережает его   0 в зависимости от соотношения между X L и X C .
1
При  L  1
C ток отстает от напряжения, при  L  C ток опережает напряжение. Если  L  1
C , изменения тока и напряжения происходят синфазно
, полное со  0 ; при удовлетворяющей этому условию частоте  рез  1
LС
противление цепи минимально (при данных R, L, C ). Соответственно, сила тока
достигает наибольшего значения (возможного при данном U m ). Падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному
к цепи. Падения напряжения на емкости U C и индуктивности U L одинаковы по
амплитуде и противоположны по фазе. Это явление называется резонансом
напряжений, а частота  рез – резонансной частотой. Явление резонанса характерно тем, что полное сопротивление цепи оказывается чисто активным и имеет
наименьшую возможную при данных параметрах цепи величину.
В цепи, по которой проходит переменный ток, выделяется мощность. При
этом мгновенное значение мощности равно произведению мгновенных значений
напряжения и силы тока:
1
1
P  t   U  t  i  t   U mCostI mCos t     U m I mCos  U m I mCos  2t   .
2
2
1
1
(Здесь учтено, что Cos Cos  Cos      Cos     .) Так как сред2
2
нее значение по времени Cos  2t    равно нулю, то среднее по времени значеU I
ние мощности составит P  m m Cos .
2
 L  1C
R
R
 . Подставив
Поскольку tg 
, то Cos 
2
Z
R
R2   L  1
C
U
значение косинуса в выражение для средней мощности, и учитывая, что m  I m ,
Z
2
RI
получим P  m . Такую же мощность развивает постоянный ток при силе тока
2
I
I  m . Это значение тока называется действующим или эффективным. Анало2
U
гично величина U  m называется действующим значением напряжения. Ис2

196

пользуя действующие значения тока и напряжения, среднюю мощность можно
представить следующим образом: P  UICos . Если реактивное сопротивление
равно нулю, то P  UI . При чисто реактивном сопротивлении цепи средняя выделяемая мощность равна нулю.
Пример 7. Конденсатор и электрическая лампочка соединены последовательно и включены в цепь переменного тока напряжением 440 В и частотой
50 Гц . Какую емкость должен иметь конденсатор для того, чтобы через лампочку
протекал ток 0,5 А и падение потенциала на лампочке было равно 110 В ?
Решение. Для того чтобы через лампочку протекал ток i  0,5 A и падение
напряжения на ней составляло U  110 B , ее сопротивление должно быть равно
R  U i  110 0,5  220  Ом  . Полное сопротивление цепи, состоящей из конденсатора
и лампочки, равно Z  R 2  1 C  2  2202  1  2  3,14  50  C 2 . В соответствии с заU
U
коном Ома i  
. Выражая отсюда C и подставляя данные заZ
R 2  1 (2 C ) 2
дачи, получаем: C  3,74 мкф .
3.5.9. Электрические цепи с изменяющимся током
Если на концы цепи, содержащей активное сопротивление R , индуктивность L и емкость C (рис. 3.5.15 а) подать переменное напряжение U  U mCost ,
то в соответствии со вторым правилом Кирхгофа будем иметь:
di q
iR  L   U mCost .
dt C
Первый член в левой части – падение напряжения на активном сопротивлении, второй – на индуктивности, третий – на емкости. Из этого уравнения как
частные случаи следуют описанные выше случаи цепей, содержащих либо только
активное сопротивление, либо только индуктивность, либо только емкость.
Этим же уравнением описываются токи при размыкании и замыкании цепи
(см. п. 3.5.4). Если цепь не содержит емкости ( q C  0 ) и U  U mCost  0 , имеем:
iR  L di dt  0 – уравнение, описывающее ток при размыкании цепи. Если
q C  0 и U  U mCost    Const , имеем: iR  L di dt   – уравнение, описывающее ток при замыкании цепи.
Рассмотрим другие частные случаи, вытекающие из приведенного общего
уравнения.
Разряд конденсатора. Если заряженный конденсатор с емкостью С замкнуть на активное сопротивление R (рис. 3.5.15 б), то он начнет разряжаться и в
цепи потечет ток, уменьшающийся по величине.
197

а)
U mCost
б)
в)
Рис. 3.5.15
Поскольку внешних источников тока нет и индуктивность отсутствует, из
общего уравнения имеем: iR  q C  0 . Учитывая, что i  dq dt , получаем:
 dq
dt  R   q C . Разделяем переменные и интегрируем: dq q   1  RC   dt 
 nq   1  RC   t  C1 . Здесь C1 – постоянная интегрирования. При t  0 заряд
на конденсаторе равен исходному q  q0 . Отсюда C1  nq0 . Далее
n  q q0    1  RC   t  q  q0e
t
. Время t  RC называется временем релаксации. За это время заряд конденсатора убывает в e раз.
Колебательный контур. Если заряженный конденсатор с емкостью С замкнуть на индуктивность L (рис. 3.5.15 в), то он начнет разряжаться, и в цепи потечет ток. Цепь, состоящая из конденсатора и индуктивности, называется колебаdi q
тельным контуром. Из общего уравнения имеем: iR  L   0 . Активное соdt C
противление катушки обычно много меньше реактивного, поэтому в расчетах коdi q
лебательного контура полагают R  0 , т. е. L   0 .
dt C
Перед началом разряда между обкладками конденсатора существует элек1 qm2
трическое поле с энергией WЭ 
(рис. 3.5.16, стадия 1), где qm – исходный за2C
ряд на обкладках.
При разряде энергия электрического поля будет уменьшаться, но зато возникнет все возрастающая энергия магнитного поля, обусловленного током, теку1
щим через индуктивность. Его энергия, как известно, равна WМ  Li 2 . Так как
2
активное сопротивление равно нулю, полная энергия не расходуется на нагревание проводника и в любой момент времени равна сумме энергий электрического и
1  q2
RC

магнитного полей: W    Li 2  . Поэтому в момент, когда напряжение на кон2 C

денсаторе, а, следовательно, и энергия электрического поля обращаются в нуль,
энергия магнитного поля, а значит, и ток достигают наибольшего значения (стадия 2). Начиная с этого момента, ток течет за счет самоиндукции, при этом величина его уменьшается. Когда заряды на обкладках достигнут исходной величины
qm , сила тока станет равной нулю (стадия 3). Затем те же процессы протекают в
198
обратном порядке (стадии 4 и 5), после чего система приходит в первоначальное
состояние и весь цикл повторяется заново. Понятно, что в рассмотренном процессе колеблются заряд на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. При этом происходят взаимные превращения энергий электрического и магнитного полей.
Рис. 3.5.16
На рис. 3.5.16 б электрическим колебаниям в контуре сопоставлены механические колебания маятника, сопровождающиеся взаимными превращениями потенциальной и кинетической энергий. Зарядка конденсатора соответствует сообщению
маятнику первоначального отклонения и, соответственно, потенциальной энергии,
которая аналогична энергии электрического поля конденсатора. При движении маятника потенциальная энергия переходит в кинетическую, соответствующую энергии магнитного поля. Индуктивность L играет роль массы m , величина 1 C – роль
коэффициента жесткости пружины k , заряду q соответствует смещение маятника
из положения равновесия x , силе тока dq dt – скорость dx dt . Эта аналогия должна
распространяться и на уравнения, описывающие процессы.
Поскольку внешнего напряжения к контуру не приложено (во время колебаний), то сумма падений напряжений на емкости U C  q C  и индуктивности
di q
U L  L di dt  должна быть равна нулю: L   0 . Разделив на L и заменив
dt C
di dt  q , получим q  02q  0 , где 0  1 LC .
199
Полученное уравнение, как известно из курса механики, описывает незатухающие свободные механические колебания. Значит, колебательные процессы
различной природы описываются одинаковыми характеристиками и одинаковыми
уравнениями. Решение этого уравнения: q  qmCos 0t    .
Таким образом, заряд на обкладках изменяется по гармоническому закону с
частотой  0 . Для периода колебаний получается, так называемая, формула Томсона: T  2 LC . Поделив заряд на емкость, получим напряжение на обкладках
q
конденсатора: U  m Cos 0t     U mCos 0t    . Продифференцировав заряд
C
по
времени,
получим
выражение
для
силы
тока:
i  0qm Sin 0t     I mCos 0t     2  . Используя выражение для  0 , легко
получить связь между амплитудными значениями напряжения и тока:
U m  L CI m .
Нетрудно показать, что и свободные затухающие и вынужденные электромагнитные колебания описываются теми же самыми уравнениями, что и соответствующие механические колебания.
Пример 8. Какую индуктивность необходимо включить в колебательный
контур, чтобы при емкости в 2 мкф получить звуковую частоту 1000 Гц ? Сопротивлением контура пренебречь.
Решение. Поскольку сопротивление контура мало, то период колебаний выражается формулой Томсона: T  2 LC . Частота колебаний обратна периоду:


  1 T  1 2 LC . Отсюда L  1  2 2 2C   0,0127 Гн .
200
IV. КОМБИНИРОВАННЫЕ ТЕСТЫ ПО ФИЗИКЕ
I. Механика
1. Из одной точки одновременно начинают двигаться два тела. Ускорение
первого тела в два раза больше чем второго.
Отношение путей, пройденных телами за одно и то же время: S1/S2=
1) 1;
2) 4;
3) 2;
4) 6.
Выберите число.
2. На рисунке показаны по оси X вектор скорости в начальный момент времени и вектор ускорения тела:
V0
хо
х
a
|Vo|=2 м/с, |а|=4 м/с2, Х0= 5 м
Выберите зависимость X (t), соответствующую такому расположению векторов:
1) X(t)= –5 + 2t – 2t2, м;
2) X(t)= 5–2t+2t2, м;
3) X(t)=5–2t–2t2, м;
4) X(t)= –5–t–2t2, м.
3. Из приведенных формул: равноускоренному движению без начальной
скорости соответствует …
1) S =V1t1+V2t2+V3t3;
2) S =V0t+at2/2;
3) S =at2/2;
4) S =V0t – at2/2.
Выберите правильный ответ.
4. Материальная точка вращается по окружности разных радиусов с одинаковой линейной скоростью: r1 = 5 см, r2 = 10 см, r3 = 15 см, r4 = 20 см. При вращении по какой окружности нормальное ускорение будет меньшим:
1) r1;
2) r2;
3) r3;
4) r4.
201
5. Сила является количественной мерой …
1) инертности тела;
2) взаимодействия тел;
3) инерции тела;
4) количества движения тела.
6. Кинетическая энергия тела, вращающегося относительно неподвижной
оси равна:
1) E = mv2/2;
2) E = Iω2/2;
3) E = mv2/2+Im2/2;
4) E = mgh.
7. Материальная точка вращается по окружности с тангенциальным ускорением равным нулю. Как будет вести себя нормальное ускорение?
1) возрастать;
2) уменьшаться;
3) будет постоянным;
4) равным нулю.
8. Вагон массой 104 кг катится по горизонтальному участку железнодорожного полотна со скоростью 1 м/с. Его нагоняет вагон массой 2·104 кг, движущийся
со скоростью 3 м/с.
Скорость сцепленных вагонов:
1) 2 м/с;
2) 3 м/с;
3) 2,3 м/с;
4) 2,8 м/с.
9. Зависимость от времени модуля скорости тела, движущегося прямолинейно, дана на рисунке:
Какой график (из приведенных) выражает соответствующую зависимость от
времени равнодействующей силы?
202
10. На рисунке показан диск радиусом R, равномерно вращающийся относительно оси, перпендикулярной плоскости диска и проходящей через точку О.
Отношение угловых скоростей точек A и B диска ωA/ωB:
1) 1/4;
2) 1;
3) 2;
4) 0.
11. Из перечисленных формул выберите формулу основного закона динамики вращательного движения твердого тела:
1) I = 1/2 mR2;
2) М = I·ε;
3) Е = Iω2/2;
4) F·Δt = m·Δv.
12. Каким будет движение тела по окружности, если тангенциальное ускорение постоянно: at=const?
1) равномерным;
2) равнопеременным;
3) равноускоренным;
4) равнозамедленным.
203
13. На каком из графиков изображенa траектория движения тела:
14. Две шестерни в зацеплении. Первая вращается с угловой скоростью ω1,
радиусы шестерен – r1, r2. Чему равна угловая скорость второй шестерни?
1) ω1 = ω2;
2) ω2=r2 ω1;
3) ω2= ω1r1/r2;
4) ω2= ω1r2/r1.
15. Что определяется при потоке идеальной жидкости формулой Торричелли?
1) давление;
2) положения линий тока;
3) скорость потока жидкости;
4) скорость истечения жидкости из малого отверстия.
16. При равномерном движении материальной точки ее скорость …
1) зависит от выбранного промежутка времени;
2) не зависит от выбранного промежутка времени;
3) определяется формой траектории;
4) можно определить только для прямолинейного движения;
17. Тело за первую половину времени своего движения двигалось со скоростью V1 , а вторую – со скоростью V2 . Средняя скорость тела Vср . –
V1V2
V1  V2
V V
2) 1 2
4
V1  V2
3)
2
2V1V2
4)
V1  V2
1)
;
;
;
.
204
18. При движении материальной точки траектория и перемещение совпадают. Можно ли утверждать, что такое движение прямолинейное?
1) нет;
2) да;
3) такое движение нереально;
4) такое движение криволинейно.
19. При неравномерном вращательном движении материальной точки угловое ускорение величина векторная?
1) нет, скалярная;
2) да;
3) нельзя определить;
4) такой характеристики нет.
20. Связь линейной скорости и угловой скорости при вращательном движении материальной точки определяется формулой:
1) V  at
2) V  V0  at
3) V  R
4) V 
S
t
21. Груз массой m поднимают на высоту h с посторонним ускорением a. Работа, совершаемая при подъеме груза A =…
1) mgh;
2) mh(g+a);
3) mah;
4) mh(g–a).
22. Тело падает на Землю с некоторой начальной скоростью V0 с высоты H.
Укажите значение скорости тела в момент соприкосновения с Землей, выраженную через заданные величины.
1) V0  2 gt ;
2) V0 2  2 Hg ;
3) V0 2  Hg ;
4) V0  gH .
23. Под действием силы тело массой М равномедленно перемещается по горизонтальной поверхности на расстояние S. Направление силы совпадает с
направлением движения, коэффициент трения  . Работа, совершаемая этой силой:
1) MgS ;
2) MgS ;
205
3) ( Mg  Mg ) S ;
4)
MgS

24. Период колебаний математического маятника равен 2c. Для того чтобы
уменьшить период колебаний до 1c необходимо …
1) увеличить амплитуду в 2 раза;
2) увеличить массу маятника в 2 раза;
3) увеличить длину маятника в 4 раза;
4) уменьшить длину маятника в 4 раза.
25. Предлагаем выбрать правильный вариант заполнения таблицы физических величин, измеренных в системе СИ.
№
Сила
Масса
1
кГ
г
2
Н
кг
3
Дж
тонна
4
Кг
кГ
Работа
Момент инерции
Мощность
Энергия
Эрг
г  см 2
Лошадиная
сила
Вт
Дж
кг  м 2
Вт
Дж
дина
Вт
кГ
Дж
Дж
м
с
Эрг
Н
дина
Импульс
см
с
м
кг 
с
г
кГ 
кг 
м
с
26. Тело брошено вертикально вверх с начальной скоростью V0 . Как определяется максимальная высота падения тела без учета сопротивления воздуха?
(Выберите вариант).
2
V
1) 0 ;
g
2
2V
2) 0 ;
g
2
V
3) 0 ;
2g
4) Нельзя определить.

27. Тело вращается вокруг точки О под действием силы F . Укажите
вари
ант (из приведенных рисунков) правильного определения плеча силы F :
206
28. При вращательном движении твердого тела по окружности действуют
 
два ускорения: нормальное и тангенциальное (an , a ) . Как направлены по отношению друг к другу в любой точке окружности векторы этих ускорений? (Укажите правильный вариант).
1) совпадают по направлению;
2) направлены в противоположные стороны;
3) направлены перпендикулярно друг к другу;
4) оба направлены к центру окружности.
29. Из перечисленных формул выберите формулу основного закона динамики вращательного движения твердого тела:
1) I  kmR2 ;
2) M  I   ;

3) F  m  a ;
4) Ek 
I 2
.
2
30. Каким будет движение тела по окружности, если тангенциальное ускорение равно нулю (a  0) ? (Выберите вариант правильного ответа).
1) неравномерным;
2) равномерным;
3) криволинейным;
4) движения не будет.
207
II. Молекулярная физика и введение в термодинамику
1. Средняя величина скорости молекул при термодинамическом равновесии
пропорциональна …
1) Т;
2)
;
3)
;
4) не зависит от температуры.
2. Внутренняя энергия моля идеального газа зависит ...
1) от давления и температуры;
2) только от температуры;
3) только от давления;
4) от температуры и числа степеней свободы молекулы.
3. Три газа: нормальный сухой воздух, воздух с повышенным содержанием
С02 и воздух с повышенной влажностью, – имеют одинаковые температуру и давление. Наибольшую плотность при этом имеет …
1) ни один из газов;
2) воздух с повышенной влажностью;
3) нормальный сухой воздух;
4) воздух с повышенным содержанием С02.
4. В сосуде неизменного объема происходит реакция: Н2 + Сl2→2НСl, после
которой температура газа принимает первоначальное значение. Давление газа при
этом...
1) не изменится;
2) возрастет;
3) уменьшится.
5. Зависимость давления от объема в процессе с некоторым количеством
идеального газа показана на рисунке:
Температура газа при этом …
1) увеличилась;
2) уменьшилась;
3) осталась неизменной.
208
6. Абсолютная температура газа увеличилась в 4 раза. При этом средняя
скорость его молекулы ...
1) уменьшилась вдвое;
2) возросла вдвое;
3) увеличилась в 4 раза;
4) увеличилась в 16 раз.
7. В ходе адиабатического расширения газа его температура
1) понижается;
2) остается неизменной;
3) повышается;
4) сначала понижается, затем повышается.
8. Энтропия системы в ходе изотермического сжатия …
1) повышается;
2) понижается;
3) остается неизменной.
9. При постоянном давлении объем идеального газа увеличился вдвое. При
этом его внутренняя энергия …
1) уменьшилась вдвое;
2) увеличилась вдвое;
3) осталась неизменной;
4) уменьшилась в 4 раза.
10. При изотермическом процессе с идеальным газом, получаемая им теплота ...
в механическую работу.
1) не превращается;
2) полностью превращается;
3) частично превращается;
4) на 1/2 превращается.
11. Выберите из приведенных выражений уравнение изобарического процесса для одного моля идеального газа:
1) P1V1=P2V2;
2) Р1Т2=Р2Т1;
3) V1T2=V2T1;
4) PV=RT.
209
12. В осях P–V изображены два состояния идеального газа.
Переведите газ из состояния 1 в состояние 2, используя изотермический и
изохорический процессы. Укажите номер соответствующего графика.
13. Идеальный газ плотностью ρ при температуре Т оказывает на стенки сосуда давление Р. Масса одной молекулы газа равна …
1) ρRT/P;
2) ρPT/R;
3) ρRT/PNA.
14. На рис. представлена зависимость температуры тела массой 1 кг от переданной ему теплоты
Удельная теплоемкость тела равна:
1) 40 Дж/кг·К;
2) 50 Дж/кг·К;
3) 45 Дж/кг·К;
4) 60 Дж/кг·К.
210
15. Из предложенных ниже формул выберите соответствующую адиабатическому процессу.
1) ΔQ = δA;
2) ΔQ = ΔU;
3) ΔQ = ΔU+δA;
4) ΔQ = 0.
16. Уравнение состояния идеального газа определяет ...
1) значение одного из параметров: P, V, T;
2) значение двух параметров;
3) связь давления P, объема V и абсолютной температуры Т;
4) протекание процесса.
17. Равновесие термодинамическое определяется …
1) неизменностью внешних условий;
2) изменением хотя бы одного термодинамического параметра;
3) возможностью перехода системы из одного состояния в другое;
4) резким изменением температуры.
18. Для определения числа молекул газа, если известна его масса m, необходимо …
1) число степеней свободы, число Авогадро;
2) молярная масса газа;
3) давление газа;
4) молярная масса газа, число Авогадро.
19. Из приведенных уравнений укажите объединенный газовый закон для
одного моля газа:
1) PV  const ;
2) V  V0  (1  t ) ;
3) PV  RT ;
4) P  const .
20. Внутренняя энергия тела складывается ...
1) только из энергии беспорядочного движения атомов и молекул;
2) из энергии беспорядочного (теплового) движения частиц и энергии их
взаимодействий;
3) из энергии взаимодействия частиц тела;
4) только из потенциальных энергий всех частиц.
21. Явление переноса в газах протекает медленно, а тепловые скорости
движения молекул газа велики. Укажите правильное объяснение.
1) в реальном макрообъеме частиц много;
2) частицы газа (атомы, молекулы) малых размеров;
3) происходит непрерывное столкновение большого числа частиц и они
меняют направление скорости;
4) энергии частиц малы.
211
22. При некоторых процессах изменение внутренней энергии равно внешней работе, совершенной над системой. Укажите этот процесс.
1) изотермический;
2) адиабатный;
3) изобарный;
4) изохорный.
23. При адиабатном процессе теплоемкость системы …
1) бесконечна;
2) имеет отрицательное значение;
3) равна нулю;
4) положительна.
24. Одноатомный и двухатомный газы имеют одинаковый объем и температуру. При адиабатном сжатии объемы газов уменьшаются в два раза. Больше
нагревается газ.
1) оба газа нагреваются одинаково;
2) температура газов не изменится;
3) одноатомный газ нагревается сильнее;
4) двухатомный газ нагревается сильнее.
25. На графике в осях P, V изображен цикл. Укажите вариант правильного
определения работы этого цикла графически.
4) нельзя определить.
212
26. Из приведенных формул укажите уравнение Ван-дер-Ваальса для произвольной массы реального газа:
a
)(V  b)  RT ;
V2
m
2) PV  RT ;
1) ( P 

m2 a
m
m
3) ( P  2 2 )(V  b)  RT ;


 V
4) U 
i m
RT .
2
27. Какие свойства частиц реального газа учитываются при определении его
термодинамического состояния?
1) скорость частиц;
2) собственный объем частиц;
3) конденсация частиц;
4) влияние сил межмолекулярного взаимодействия, собственный объем
частиц.
28. Теплоемкость идеального газа ...
1) выше в процессе 1–2;
2) выше в процессе 1–3;
3) одинакова в обоих процессах;
4) определить нельзя.
29. Повысить к.п.д. теплового двигателя можно, …
1) повысив температуру холодильника;
2) повысив температуру нагревателя;
3) увеличив массу рабочего тела;
4) увеличив число циклов в единицу времени.
30. Какое количество теплоты выделяется при торможении автомобиля массой 1000 кг, имеющего начальную скорость 10 м/с?
1) 10 кДж;
2) 50 кДж;
3) 100 кДж;
4) 500 кДж.
213
III. Электричество и магнетизм
1. Какую характеристику электрического поля можно определить моделью
точечного, единичного положительного заряда?
1) величину другого заряда;
2) направление вектора напряженности электрического поля;
3) энергию электрического поля;
4) электроемкость.
2. Модель диполя –
1) два отрицательных заряда;
2) два одинаковых по знаку заряда;
3) два заряда разной величины одинакового знака;
4) два равных по величине, разных по знаку заряда, расстояние между
которыми много меньше до рассматриваемых точек его электрического поля.
3. Какие свойства электрического поля определяет потенциал?
1) силовые;
2) знак заряда;
3) энергетические;
4) тепловые.
4. Какой из векторов будет определять суммарную напряженность электрического поля в точке А для изображенного диполя?
1) вектор E;
2) вектор Е1;
3) ни один из векторов;
4) вектор Е2.
5. Силовые линии электростатического поля ...
1) замкнуты;
2) начинаются на положительных зарядах или в бесконечности и заканчиваются на отрицательных зарядах или в бесконечности;
3) начинаются на отрицательных зарядах или в бесконечности и заканчиваются на положительных зарядах или в бесконечности;
4) имеют спиральный вид.
214
6. Напряженность электрического поля внутри проводника ...
1) обратно пропорциональна расстоянию от поверхности проводника до
рассматриваемой точки;
2) равна нулю;
3) тем больше, чем больше напряженность электрического поля вне проводника;
4) тем меньше, чем меньше напряженность электрического поля вне
проводника.
7. Свойство проводника накапливать заряды в электрическом поле называется ...
1) проводимостью;
2) электроемкостью;
3) электризацией;
4) сопротивлением.
8. Емкость плоского конденсатора тем больше, чем ...
1) больше площадь пластин конденсатора;
2) больше расстояние между пластинами конденсатора;
3) больше разность потенциалов между пластинами конденсатора;
4) меньше диэлектрическая проницаемость вещества между пластинами
конденсатора.
9. Два резистора соединены последовательно. Сила тока в первом резисторе
равна 0,5 А. Сила тока во втором резисторе равна ...
1) 1А;
2) 2А;
3) 0,5А;
4) 3А.
10. Два резистора соединены параллельно. Ток, подходящий к резисторам,
равен 3А. Сила тока в одном резисторе равна 1А. Сила тока во втором резисторе
равна ...
1) 4А
2) 2А
3) 1,5А
4) 2,5А
11. Из представленных формул выберите ту, которая определяет плотность
тока в проводнике:
1) I = U/R;
2) I = ξ/RT;
3) P = I·U;
4) j = σЕ.
215
12. Каким прибором (из предложенных) можно определить магнитное поле
вокруг проводника с током?
1) амперметром;
2) вольтметром;
3) магнитной стрелкой;
4) гальванометром.
13. На проводник с током в магнитном поле действует сила Ампера. С помощью какой формулы (из приведенных) ее можно определить?
1) B = ρμ0H;
2) H = I/2 R;
3) F = eE;
4) F = I·B·l·sinα.
14. Укажите номер рисунка, на котором сила Лоренца имеет правильное
направление.
15. Какой процесс обеспечивают носители зарядов при протекании тока через электролит?
1) свечение молекул растворенного вещества;
2) диссоциация молекул растворенного вещества;
3) выделение вещества на электродах ванны;
4) кипение раствора.
16. В цепях переменного тока в ... напряжение опережает ток на угол π/2.
1) резисторе;
2) индуктивности;
3) конденсаторе;
4) последовательно соединенных резисторе и конденсаторе.
17. В цепи генератора переменного напряжения резонанс тока может быть
реализован ...
1) в последовательно включенных конденсаторе и индуктивности;
2) параллельно включенных резисторе и конденсаторе;
216
3) параллельно включенных конденсаторе, индуктивности и резисторе;
4) в резисторе.
18. Запишите название всех элементов схем электрической цепи:
1) С, L, R, Е, ε;
2) L, С, R, ε, Т;
3) R, С, L, Т, ε;
4) Е, L, С, R, ε.
19. Какая из формул определяет энергию магнитного поля индуктивности?
1) W = CU2/2;
2) W = LI2/2;
3) W = mV2/2+mgh;
4) W = q2/2C.
20. Два параллельных проводника, по которым текут токи в одинаковом
направлении, ...
1) отталкиваются;
2) не взаимодействуют;
3) притягиваются;
4) вопрос некорректен.
21. Основной характеристикой электрического диполя является …
1) заряд диполя;
2) электрический момент;
3) энергия диполя;
4) напряженность диполя.
22. Из приведенных формул укажите формулу, определяющую поверхностную плотность заряда.
q
;
V
q
2)   ;
S
1)  
217
q
;
L
M
.

V
3)  
4)
23. Электрический потенциал – скалярная величина, определяющая …
свойства электростатического поля.
1) силовые;
2) зарядовые;
3) энергетические;
4) динамические.
24. Как расположены силовые линии электростатического поля по отношению к эквипотенциальным поверхностям?
1) по касательной к поверхности;
2) под произвольным углом к поверхности;
3) вопрос некорректен;
4) под углом П/2.
25. Плоский воздушный конденсатор после зарядки отключают от источника напряжения и погружают в трансформаторное масло. Энергия конденсатора …
1) не изменится;
2) уменьшится в два раза;
3) увеличится в число раз, равное диэлектрической проницаемости масла;
4) уменьшится в число раз, равное диэлектрической проницаемости масла.
26. Электрическое напряжение – скалярная величина равная работе, совершаемой суммарным полем ... при перемещении единичного положительного заряда на участке электрической цепи.
1) электростатических и магнитных сил;
2) электростатических и консервативных сил;
3) потенциальных и сторонних сил;
4) кулоновских и сторонних сил.
27. При электролизе используется понятие «число Фарадея». В чем физический смысл числа Фарадея?
1) определяет направление движения ионов;
2) определяет химический эквивалент;
3) определяет величину заряда, прохождение которого через электролит
приводит к выделению 1 моля вещества на электродах;
4) определяет величину заряда, прохождение которого 1 иона вещества
на электродах.
28. Произвольная рамка вращается в одном магнитном поле. Ось вращения
совпадает с направлением вектора индукции поля. Э.д.с. индукции в рамке …
218
1) индуцироваться будет;
2) индуцироваться не будет;
3) индуцироваться будет произвольная э.д.с.;
4) вопрос не корректен.
29. Индуктивность колебательного контура равна 0,5 мГн. Определите емкость конденсатора, если контур резонирует на длину волны 300 м.
1) 100 мкф;
2) 100 пф;
3) 50 пф;
4) 50 нф.
30. Определить угловую скорость обращения электрона по окружности, которую он описывает в однородном магнитном поле индукции 2  10 2 Тл. Массу
электрона принять равной 9,1  10 31 кг.
рад
;
с
рад
;
3,5  10 9
с
рад
;
6  10 9
с
рад
.
1,5  1010
с
1) 6  10 8
2)
3)
4)
219
ПРИЛОЖЕНИЕ
Некоторые характеристики Солнца, Земли, Луны
Физические параметры
Солнце
Земля
Луна
Масса, кг
1,97·1030
5,96·1024
7,33·1022
Радиус, м
6,95·108
6,37·106
1,74·106
Средняя плотность, кг/м3
1400
5518
3350
Среднее расстояние от Земли,
км
1,496·108
–
384 440
Плотность (кг/м3)
Газы (при нормальных условиях)
0,08988 Воздух
1,293 Кислород
1,977
Водород
Углекислый газ
Жидкости
Бензол
880
Касторовое масло
Серебро
Ртуть
Твердые тела
950
9300
13 600
Алюминий
2600
Каменная соль
Медь
Платина
Серебро
2200
8600
21 400
10 500
Вода
(+4С)
Керосин
Спирт
1,429
1000
Глицерин 1200
800
790
Кровь
Золото
1050
17 200
Железо
7900
Золото
19 300
Латунь
Никель
Пробка
Сталь
8400 Лед
8800 Олово
200
Свинец
7700 Стекло
900
7100
11 300
2700
Плотность воды при различных температурах
Температура, °С
Плотность, кг/м3
20
998
30
996
40
992
50
988
60
983
70
978
80
972
Модуль упругости (Гпа)
Алюминий
70
Латунь
90
Чугун
100
Дерево
Дуралюминий
Кирпич
10
75
10
Медь
Свинец
Сталь (железо)
120
17
210
Каучук
0,008
220
Диаметры молекул и атомов (нм)
Азот (N2)
Аргон(Ar)
Водород (Н2)
0,31
0,29
0,23
Водяной пар (Н2О)
Гелий (Не)
Кислород (О2)
0,26
0,19
0,29
Оксид углерода (СО)
Углекисл. газ (СО2)
Хлор (Сl2)
0,32
0,33
0,37
Удельная теплоемкость с, Дж/(кг·К)
Твердые и жидкие тела
с
Вещество
с
Вещество
896 Железо (сталь) 460
Ртуть
2095
Латунь
386
Свинец
130
Лед
2100
Спирт
1800
Масло (20С)
195
Медь
395
Вещество
Алюминий
Бензин (50С)
Висмут
Вода (20С)
Вольфрам
с
138
131
2510
Газы и пары
Вещество
Аммиак (NH3)
Аргон (Ar)
Воздух
Гелий (He)
Кислород (O2)
Метан (CH4)
Пары воды (H2O)
Углекислый газ (СO2)
ср, Дж/(кг·К)
2140
532
1020
5240
913
2373
1820
848
cv, Дж/(кг.К)
1630
320
729
3140
649
1854
1380
654
 = cр/сv
1,31
1,66
1,40
1,66
1,40
1,28
1,32
1,30
Вязкость жидкостей, газов и паров
Вещество
Температура, С
Азот
Вода
Воздух
Гелий
0
20
21,6
0
Вязкость,
мкПа·с
16,7
1004
18,4
18,6
Вещество
Температура, С
Кислород
Пары воды
Углекисл. газ
Хлор
0
0
0
0
Вязкость,
мкПа·с
19,2
8,7
13,7
12,9
Постоянные Ван-дер-Ваальса
Вещество
a, Дж.м3/моль2
Азот
Аргон
Вода
0,136
0,132
0,554
b·10–5,
м3/моль
4
3
3
221
Вещество
a, Дж.м3/моль2
Кислород
Углекисл.
газ
0,137
b·10–5,
м3/моль
3
0,364
4,3
Критические значения температуры и давления
Вещество
Азот
Аргон
Бензол
Водород
Тк, К
126
151
562
33
Рк, МПа
3,4
4,87
4,8
1,3
Вещество
Водяной пар
Гелий
Кислород
Углекисл. газ
Тк, К
647
5.2
154
304
Рк, МПа
22,0
0,23
5,07
7,4
Поверхностное натяжение жидкостей при 20С (мН/м)
Вещество
Анилин
Бензол
Вода
Вода
(70С)

43
30
73
Вещество
Глицерин
Золото (1070С)
Касторовое масло

64
610
33
Вещество
Мыльный р-р воды
Ртуть
Серебро

45
500
780
64
Керосин
30
Спирт
22
Теплопроводность веществ (Вт/(м·К)
Вещество
Алюминий
Аргон
Асбест
Висмут
Вода
Воздух
Вещество
Дерево
Железо (сталь)
Кирпич. кладка
Медь
Накипь котельная
Пробка
q
205
0,16
0,14
10
0,58
0,026
q
0,17
62
0,84
390
2,3
0,035
Вещество
Сажа
Свинец
Смола
Стекло
Эбонит
q
0,25
34,8
0,52
0,74
0,16
Температура плавления (Т,С) и удельная
теплота плавления (,кДж/кг)
Вещество
Т
Алюминий 660
Железо
1535
Лед
0
Медь
1083
Олово
232

387
272
334
174
60
Вещество
Ртуть
Свинец
Серебро
Цинк
222
Т
–38,9
327
960
420

11,7
25
80
118
Учебное издание
Владимир Васильевич Алексеев
Валерий Григорьевич Приданов
ФИЗИКА
Часть 1
учебно-методический комплекс для студентов ОЗО
факультета технологии и предпринимательства НГПУ
Редактор Е. А. Бутина
Компьютерная верстка Е. В. Кубракова
Подписано в печать 17.06.2009. Формат бумаги 60х84/8. Печать RISO.
Уч.-изд.л. 27,5. Усл. печ. л. 25,57. Тираж 150 экз. Заказ № 24.
Педуниверситет, 630126, г. Новосибирск, 126, Вилюйская, 28
223