шпаргалку по начертательной геометрии
advertisement
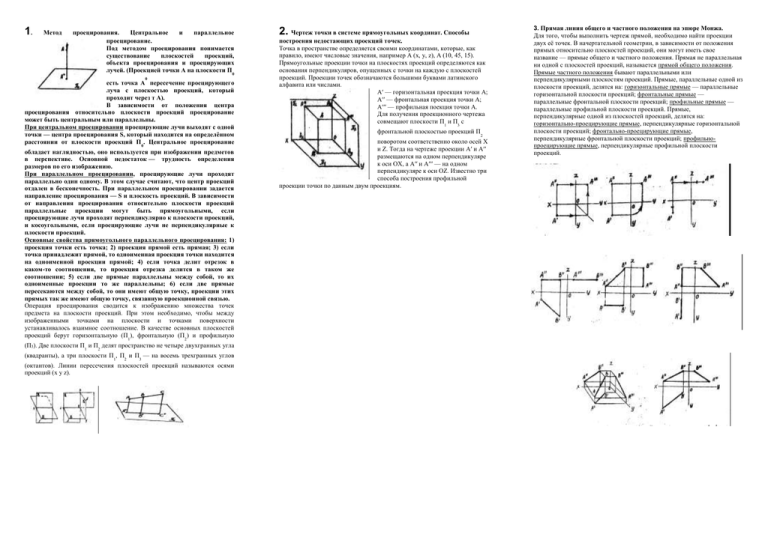
1. Метод проецирования. Центральное и параллельное проецирование. Под методом проецирования понимается существование плоскостей проекций, объекта проецирования и проецирующих лучей. (Проекцией точки А на плоскости П0 0 есть точка А пересечение проецирующего луча с плоскостью проекций, который проходит через т А). В зависимости от положения центра проецирования относительно плоскости проекций проецирование может быть центральным или параллельны. При центральном проецировании проецирующие лучи выходят с одной точки — центра проецирования S, который находится на определённом расстоянии от плоскости проекций П . Центральное проецирование 0 обладает наглядностью, оно используется при изображении предметов в перспективе. Основной недостаток — трудность определения размеров по его изображению. При параллельном проецировании, проецирующие лучи проходят параллельно один одному. В этом случае считают, что центр проекций отдален в бесконечность. При параллельном проецировании задается направление проецирования — S и плоскость проекций. В зависимости от направления проецирования относительно плоскости проекций параллельные проекции могут быть прямоугольными, если проецирующие лучи проходят перпендикулярно к плоскости проекций, и косоугольными, если проецирующие лучи не перпендикулярные к плоскости проекций. Основные свойства прямоугольного параллельного проецирования: 1) проекция точки есть точка; 2) проекция прямой есть прямая; 3) если точка принадлежит прямой, то одноименная проекция точки находится на одноименной проекции прямой; 4) если точка делит отрезок в каком-то соотношении, то проекция отрезка делится в таком же соотношении; 5) если две прямые параллельны между собой, то их одноименные проекции то же параллельны; 6) если две прямые пересекаются между собой, то они имеют общую точку, проекции этих прямых так же имеют общую точку, связанную проекционной связью. Операция проецирования сводится к изображению множества точек предмета на плоскости проекций. При этом необходимо, чтобы между изображенными точками на плоскости и точками поверхности устанавливалось взаимное соотношение. В качестве основных плоскостей проекций берут горизонтальную (П1), фронтальную (П2) и профильную (П3). Две плоскости П1 и П2 делят пространство не четыре двухгранных угла (квадранты), а три плоскости П1, П2 и П3 — на восемь трехгранных углов (октантов). Линии пересечения плоскостей проекций называются осями проекций (x y z). 2. Чертеж точки в системе прямоугольных координат. Способы построения недостающих проекций точек. Точка в пространстве определяется своими координатами, которые, как правило, имеют числовые значения, например А (x, y, z), А (10, 45, 15). Прямоугольные проекции точки на плоскостях проекций определяются как основания перпендикуляров, опущенных с точки на каждую с плоскостей проекций. Проекции точек обозначаются большими буквами латинского алфавита или числами. А′ — горизонтальная проекция точки А; А′′ — фронтальная проекция точки А; А′′′ — профильная поекция точки А. Для получения проекционного чертежа совмещают плоскости П и П с 1 3 фронтальной плоскостью проекций П 2 поворотом соответственно около осей X и Z. Тогда на чертеже проекции А′ и А′′ размещаются на одном перпендикуляре к оси ОX, а А′′ и А′′′ — на одном перпендикуляре к оси ОZ. Известно три способа построения профильной проекции точки по данным двум проекциям. 3. Прямая линия общего и частного положения на эпюре Монжа. Для того, чтобы выполнить чертеж прямой, необходимо найти проекции двух её точек. В начертательной геометрии, в зависимости от положения прямых относительно плоскостей проекций, они могут иметь свое название — прямые общего и частного положения. Прямая не параллельная ни одной с плоскостей проекций, называется прямой общего положения. Прямые частного положения бывают параллельными или перпендикулярными плоскостям проекций. Прямые, параллельные одной из плоскости проекций, делятся на: горизонтальные прямые — параллельные горизонтальной плоскости проекций; фронтальные прямые — параллельные фронтальной плоскости проекций; профильные прямые — параллельные профильной плоскости проекций. Прямые, перпендикулярные одной из плоскостей проекций, делятся на: горизонтально-проецирующие прямые, перпендикулярные горизонтальной плоскости проекций; фронтально-проецирующие прямые, перпендикулярные фронтальной плоскости проекций; профильнопроецирующие прямые, перпендикулярные профильной плоскости проекций. 4. Следы прямой линии. Сформулировать последовательность построения горизонтального и фронтального следов прямой. Следом прямой линии называется точка пересечения прямой с соответствующей плоскостью проекций. Для определения горизонтального следа М (М′, М′′) прямой АВ (А′В′, А′′В′′) надо: продлить фронтальную проекцию А′′В′′ до пересечения с осью ОХ (М′′), затем повести перпендикуляр к оси ОХ до пересечения с продолжением горизонтальной проекции А′В′. Для определения фронтального следа N (N′, N′′) прямой надо: продлить горизонтальную проекцию А′В′ до пересечения с осью ОХ, затем провести перпендикуляр к оси ОХ до пересечения с подолжением фронтальной проекции А′′В′′. М (М′, М′′) — горизонтальный след рпямой АВ (А′В′, А′′В′′); N (N′, N′′) — фронтальный след прямой АВ (А′В′, А′′В′′). 5. Определение истинной величины отрезка прямой общего положения способом прямоугольного треугольника. Натуральная величина отрезка прямой общего положения определяется как гипотенуза прямоугольного треугольника, одним катетом которого является проекция отрезка на одну из плоскостей проекций, а второй катет равен разности расстояний концов отрезка до этой же плоскости. φ — угол наклона отрезка АВ к плоскости проекций П ; 1 1 φ — угол наклона отрезка АВ к плоскости проекций П . 2 2 6. Взаимное положение точки и прямой, двух прямых. Определение видимости проекций точек на скрещивающихся прямых. Точка и прямая в пространстве занимают разное положение относительно друг друга. С (С′, С′′) — находится над прямой АВ. D (D′, D′′) — находится под прямой АВ. E (E′, E′′) — принадлежит прямой АВ. F (F′, F′′) — находится за прямой АВ. Две прямые в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Если прямые параллельные, то их соответствующие проекции то же параллельные (А′В′//, С′D′, А′′В′′//С′′D′′). Если две прямые пересекаются, то они имеют общую точку. Проекции этой точки дожны лежать на одной линни связи. Если две прямые не параллельные и не пересекаются, то они скрещивающиеся. Проекции этих прямых на чертеже могут пересекаться, но точки пересечения их проекций не лежат на одной линии связи. Видимость проекций прямых, которые скрещиваются, определяется по правилу конкурирующих точек — точек, принадлежащих скрещивающимся прямым и расположенных на одной и той же проецирующей прямой. Видимость фронтальных проекций определяется видимостью конкурирующих точек 1 и 2. В этом случае видимой, ближайшей к наблюдателю, является проекция С′D′. Видимость горизонтальных проекций прямых определяется видимостью конкурирующих точек 3 и 4. видимой проекцией здесь является А′В′. 7. Способы задания плоскостей. Плоскости частного и общего положения на эпюре Монжа. Плоскостью называется множество точек равноудалённых от двух точек пространства. Плоскость задается следующим образом: 1)проекциями трех точек, не лежащих на одной прямой; 2) проекцией прямой и точки, не лежащей на прямой; 3) проекцией плоской фигуры; 4) проекциями двух прямых, которые пересекаются; 5) проекциями двух параллельных прямых; 6) следами плоскости (линия пересечения заданной плоскости с плоскостью проекций называется следом). Плоскости относительно плоскостей проекций могут занимать общее и частное положения. Плоскости, не перпендикулярные ни одной из плоскостей проекций, называется плоскостью общего положения. Плоскости частного положения делятся на проецирующие плоскости, перпендикулярные к одной из плоскостей проекций, и на плоскости, параллельные одной из плоскостей проекций. Проецирующие плоскости делятся на: 1) горизонтально-проецирующие, перпендикулярные к плоскости проекций П1; фронтально-проецирующие, перпендикулярные к плоскости проекций П2; профильно-проецирующие, перпендикулярные к плоскости проекций П3. Проецирующие прямые обладают собирательным свойством, а именно: все геометрические образы, принадлежащие плоскости, проецируются в линию на ту плоскость, перпендикулярно которой она размещена. Плоскости, параллельные плоскостям проекций, делятся на: горизонтальные, фронтальные, профильные. 8. Горизонтали и фронтали плоскости. Точка и прямая в плоскости. Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости. Например, точка D (D′, D′′) принадлежит плоскости АВС (А′В′С′, А′′В′′С′′), т. к. она лежит на прямой С1 (С′1′, С′′1′′). Прямая принадлежит плоскости, если две ее точки принадрежат плоскости. Прямая принадлежит плоскости, если она проходит через одну точку этой плоскости и параллельна какой-нибудь прямой, лежащей в плоскости. К числу прямых, которые занимают особое положение в плоскости, относят горизонтали и фронтали. Горизонталями плоскости называют прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций. Фронталями плоскости называют прямые, принадлежащие плоскости и параллельные фронтальной плоскости проекций. 9. Взаимное положение прямой и плоскости (прямые параллельные и перпендикулярные плоскости). Проецирование прямого угла. 10. Взаимное положение двух плоскостей. Построение линии пересечения плоскостей при различных способах их задания. Две плоскости параллельны, если две пересекающие прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Если плоскость задана следами, то параллельность определяется параллельностью соответственных следов. Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости, или перпендикулярна к прямой, лежащей в другой плоскости. Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, принадлежащей данной плоскости. Прямая перпендикулярна к плоскости, если она перпендикулярна ко всем двум прямым, которые пересекаются в этой плоскости принадлежат ей. Но, чтобы при этом проекция перпендикуляра к плоскости общего положения оказалась перпендикулярной к соответственной проекции некоторой прямой этой плоскости, прямая должна быть горизонталью или фронталью, или профильной прямой плоскости. Поэтому, если надо построить перпендикуляр к плоскости, берут в общем случае две такие прямые. Таким образом, у перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проекции фронтали. Очевидно, если плоскость задана следами, мы получаем следующий результат: если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоскости. Если через точку D надо провести прямую L (1′, 1″), перпендикулярную к плоскости, заданой АВС нужно выполнить следующие построения: 1) Провести в плоскости горизонталь С1 (С′1′, С″1″) и фронталь А2 (А′2′, А″2″); 2) Через горизонтальную проекцию D′ точки D провести прямую 1′, перпендикулярную к горизонтальной проекции горизонтали С′1′, — это будет горизонтальная проекция перпендикуляра; 3) Через фронтальную проекцию D″ точки D провести прямую 1″, перпендикулярную к фронтальной проекции фронтали А″2″, — фронтальная проекция перпендикуляра. Построенная прямая L (1′, 1″) и есть перпендикуляр к плоскости АВС. На основании перпендикулярности прямой и плоскости можно решать следующие задачи: определять расстояние в пространстве; определять расстояние между двумя параллельными плоскостями; проводить плоскость, параллельную данной, находящейся на некотором расстоянии; из точки, лежащей в плоскости, строить перпендикуляр к ней; проводить через точку плоскость, перпендикулярную к данной плоскости. Теоретической основой для построения на чертежах проекций прямых и плоскости, перпендикулярных относительно к друг другу, служит теорема о проецировании прямого угла. В общем случае угол проецируется на плоскость в натуральную величину, если две его стороны параллельны этой плоскости. Прямой угол проецируется в натуральную величину, если хотя бы одна его сторона параллельна плоскости проекций, а другие не перпендикулярны к этой плоскости. Таким образом, возможно три случая проецирования прямого угла на плоскость: 1) 2) 3) Если две стороны прямого угла заданы прямыми общего положения, то прямой угол проецируется с искажением на все три плоскости проекций; Если две стороны прямого угла параллельны какой-нибудь плоскости проекций, то на эту плоскость прямой угол проецируется в натуральную величину; Если одна сторона прямого угла прямая общего положения, а другие параллельны плоскости проекций, то прямой угол проецируется на эту плоскость проекций в прямой. Две плоскости пересекаются по прямой. В зависимости от, того какое положение занимают плоскости, возможно три случая пересечения плоскостей: 1) Две плоскости занимают частное положение. Возможно два варианта: 1) две пересекающиеся плоскости перпендикулярны к одной плоскости проекций линия пересечения перпендикулярна к этой же плоскости проекций; 2) две пересекающиеся плоскости перпендикулярны к разным плоскостям проекций линия пересечения есть линия, проекция которой совпадает со следами плоскостей. 2) Одна из плоскостей занимает общее положение, а другая — частное одна проекция линии пересечения совпадает со следом плоскости частного положения, а другая проекция определяется из условия принадлежности этой прямой плоскости общего положения. 3) Две плоскости занимают общее положение. Построение линии пересечения плоскостей при различных способах их задания: Провести вспомогательную плоскость, пересекающую две данных плоскости ( плоскость частного положения); Определить линии пересечения вспомогательных плоскостей с каждой из данных плоскостей; Найти точки пересечения полученных линий и соединить их. 11. Правила построения точки пересечения прямой с плоскостью. Определение видимости прямой. Правила построения точки пересечения прямой с плоскостью: Через прямую провести вспомогательную плоскость; Определить линию пересечения заданной и вспомогательной плоскостей; Определить точку пересечения прямой с плоскостью как результат заданной прямой с найденной точкой пересечения; Определить видимость прямой. 12. Аксонометрические проекции. Основные понятия и определения. Построение окружности в аксонометрических проекциях. Способ аксонометрического проецирования заключается в том, что проецирующую фигуру соотносят с некоторой системой прямоугольных координат и вместе с этой системой параллельно проецируют на одну плоскость проекций. Прямые ОХ, О, О — оси координат в пространстве, прямые ОХ, О, О — их проекции на плоскость , которые называются аксонометрическими осями. На осях Х, , отложены некоторые отрезки длиной L, принимающиеся за единицу измерения на этих осях. Отрезки lx, ly, lz на аксонометрических осях есть проекции отрезка l . Отношения lx/l, ly/l, lz/l называются коэффициентами искажения по аксонометрическим осям. Коэффициенты искажения по оси О Х обозначим k, по оси О — m, по оси О — n. В зависимости от соотношения коэффициентов искажения проекции делятся на : изометрическую (k=m=n), диметрическую (k≠m=n), триметрическую (k≠m≠n). В зависимости от угла между направлением проецирования и аксонометрической плоскостью аксонометрические проекции могут быть косоугольными и прямоугольными. 13. Стандартные виды аксонометрических проекций. Коэффициенты искажения. Построение окружности в аксонометрических проекциях. ГОСТ 2.317–69 рекомендует использовать следующие аксонометрические проекции: прямоугольная изометрическая проекция; прямоугольная диметрическая проекция; косоугольная фронтальная диметрическая проекция; косоугольная фронтальная изометрическая проекция; косоугольная горизонтальная изометрическая проекция. Прямоугольная изометрическая проекция. Аксонометрические оси в изометрии размещены под углом 120° одна от другой, причем ось Z размещается всегда вертикально. Коэффициенты искажения по всех осях равны между собой: k=m=n, k²+m²+n²=3k²=2 k=0,82. Для упрощения построения принимают коэффициенты искажения равными единицы. В этом случае аксонометрическая проекция получается увеличенной в 1,22 раза относительно натуральной величины предмета. Окружность, размещенная в координатных плоскостях или плоскостях, которые им параллельны, проецируются в виде эллипсов. Большая полуось АВ размещается перпендикулярно к той сои, которой нет в плоскости размещения окружности. Размеры осей эллипсов: большая полуось — АВ=1,22d; малая ось — CD=0,7d, где d — диаметр проецируемой окружности. Прямоугольная диметрическая проекция. В прямоугольной диметрической проекции ось Х размещается под углом 7°10´ к горизонтальной линии, ось Y под углом 41º25´ к этой же линии. Ось Z — вертикально. Коэффициенты искажения по осях Х и Z равны между собой, а по оси Y=0,5, k=n; m=½k. Тогда равенство k²+m²+n²=2k²+¼k²=2 k=0,94. Для построения принимают коэффициенты искажения по осях X и Z=1, по оси Y=0,5. Построены чертеж при этом получается увеличенным в 1,06 раз. Окружности, находящиеся в координатных плоскостях, как и в изометрии, проецируются в виде эллипсов. В плоскостях ХОY и ZOY или им параллельных эллипсы по форме и размерах одинаковы. Большая ось АВ=1,06d, малая ось CD=0,35d. В плоскости ХОY большая ось АВ=1,06d, малая ось CD=0,35d (d — диаметр окружности). Большая ось размещается перпендикулярно к отсутствующей оси плоскости размещения окружности. Косоугольные аксонометрические проекции. Часто применяется такая косоугольная диметрия, коэффициенты искажения которой по оси Y принимаются равными 0,5, а угол между этой осью и другими осями равен 135°. Такая аксонометрия называется фронтальной диметрической проекцией. Особенностью данной проекции является то, что окружность проецируется без искажения на фронтальную плоскость проекций. 14. Способы преобразования проекций. Способ плоскопараллельного перемещения. Способы преобразования проекций: перемена плоскостей проекций; вращение вокруг проецирующей прямой; вращение вокруг линий уровня; плоскопараллельное перемещение; совмещение. Задачи: а) прямая общего положения преобразуется в прямую уровня; б) прямая уровня преобразуется в проецирующую прямую; в) плоскость общего положения преобразуется в проецирующую плоскость; г) проецирующая плоскость преобразуется в плоскость уровня. Способ плоскопараллельного перемещения. Сущность этого способа заключается в перемещении геометрической фигуры относительно данных плоскостей проекций в частное положение таким образом, чтобы траектория перемещения всех ее точек находилась в параллельных плоскостях. Плоскопараллельное перемещение — общий случай вращения без указания местоположения оси. При параллельным переносе геометрической фигуры относительно плоскостей проекций проекция фигуры на эту плоскость хоть и изменяет свое положение, но не изменяется по форме и размерах. 15. Способ замены плоскостей. Сущность этого способа заключается в переходе от данной системы плоскостей проекций П1/П2 к новой. Проецируемая фигура при этом не меняет своего положения в пространстве. Одна из основных плоскостей проекций П1 или П2 заменяется новой плоскостью, размещенной определенным образом относительно неподвижного объекта проецирования. Поскольку в новой системе плоскостей проекций проецирование остается прямоугольным, то новая плоскость должна быть перпендикулярной к незамененной плоскости проекций П1 или П2. 16. Способ вращения вокруг проецирующих прямых. 17. Пересечение многогранников плоскостью частного положения. 18. Развертки поверхностей. Развертывание поверхности Сущность способа заключается в том, что данная система плоскостей проекций остается неизменной, а проецируемую фигуру вращают вокруг неподвижной оси, перпендикулярной к одной из плоскостей проекций, до той пары, пока она не займет частное положение, т.е. при вращении плоскость сохраняет свое первоначальное положение, а геометрический образ перемещается в пространстве. Центр вращения — точка пересечения оси вращения с плоскостью вращения. Радиус вращения — расстояние от центра вращения до заданной точки. Cечение — изображение фигуры, полученной в секущей плоскости. Способ ребер подразумевает определение точек пересечение ребер с заданной плоскостью. Способ граней определяет линии пересечения граней многогранника с заданной плоскостью. многогранников. Развертка — плоская фигура, получающаяся при совмещении поверхности с плоскостью. При совмещении всех граней многогранника с плоскостью в такой последовательности, в которой они размещены в многограннике, получается развертка его поверхности. Для построения развертки нужно найти натуральную величину всех граней многогранника и фигуры сечения. Три вида разверток: точные (призмы, пирамиды); приближенные (поверхности вращения заменяют многогранной поверхностью); условные (поверхности заменяются абсолютно другой). 19. Пересечение кривых поверхностей плоскостью частного 20. Развертывание поверхности прямого кругового конуса и положения. Линии конических сечений. цилиндра. Для построения развертки усеченной цилиндрической поверхности на горизонтальной прямой откладывают длину окружности основания, равную D, и делят ее на 12 равных частей. Из точек деления восстанавливают перпендикуляры к отрезку D, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки соединяют плавной кривой. Затем пристраивают фигуру сечения и фигуру нижнего основания (окружность). При пересечении цилиндра плоскостью, параллельной оси, получается плоская фигура в виде прямоугольника или параллелограмма. Если секущая плоскость перпендикулярна к оси цилиндра, то в результате сечения этой плоскостью получается круг. В общем случае, если секущая плоскость наклонена к оси цилиндра, в сечении поучается эллипс. При пересечении конуса секущей плоскостью, в зависимости от ее направления получаются разные фигуры, ограниченные линиями, которые называются линиями конических сечений. Если секущая плоскость проходит через вершину конуса, в его сечении получается треугольник. В результате пересечения конуса плоскостью, перпендикулярной к его оси вращения, получается круг. Если плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении, в результате от величины угла наклона секущей плоскости к оси конуса, получатся: при — эллипс; при — ограниченная парабола; при — ограниченная гипербола, где — половина угла при вершине конуса. 21. Цилиндрические и конические винтовые линии. Образование, основные параметры. Построение развертки поверхности конуса начинают с нанесения из какойлибо точки S дуги окружности радиусом, равным длине образующей конуса. На этой дуге откладывают 12 частей окружности основания и полученные точки соединяют с вершиной прямыми образующими. От вершины S на прямых откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости. К развертки конической поверхности пристраивают фигуры сечения и основания конуса. Для более точного построения развертки конической поверхности прямого кругового конуса центральный угол сектора, представляющего эту развертку, можно посчитать по формуле dl, где d — диаметр окружности основания конуса в мм, l — длина образующей конуса в мм. Цилиндрические винтовые линии образуются на поверхности цилиндра вращения при равномерном перемещении точки вдоль его образующей и при одновременном равномерном вращении образующей около оси цилиндра. Проекции цилиндрической винтовой линии: фронтальная — синусоида, горизонтальная — окружность. Фронтальная проекция строится следующим образом: делим окружность основания цилиндра и шаг винтовой линии (отрезок, на который подымается точка А при полном повороте образующей цилиндра) на одинаковое количество частей (12). Определяем соответственные фронтальные проекции перемещающейся точки и соединяем их плавной кривой. При развертки цилиндрической поверхности винтовая линия является прямой. Угол называется углом подъема винтовой линии: tg=h/D, где h — шаг линии, D — диаметр цилиндра. Винтовая линия на цилиндрической поверхности имеет постоянный подъем. Коническая винтовая линия образуется на поверхности конуса вращения при равномерном перемещении точки вдоль его образующей и при одновременном равномерном вращении образующей около конуса. Проекции конической винтовой линии (горизонтальная спираль Архимеда, а фронтальная — затухающая синусоидальная кривая с уменьшающейся длиной волны) строится следующим образом: делим окружность основания конуса и шаг винтовой линии на одинаковое количество частей (12). Определяем по соответственным образующим конуса местоположение проекций точек 1, 2, …, 12 и соединяем их плавной кривой. Винтовые линии могут быть правыми и левыми. Правой называется винтовая линия, которая подымается слева вверх направо. Левая винтовая линия подымается справа вверх налево. Часть винтовой линии, соответствующая одному ее шагу, называется витком. Винтовые линии, образованные на цилиндре и конусе, имеют большое практическое значение в практике (используются для образования резьб). 22. Поверхности. Классификация, определитель и каркасы 23. Поверхности вращения. Построение точки на поверхности 25. Построение точки пересечения прямой с поверхностью (общий поверхностей. Поверхностью называется совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Эту линию называют образующей. Перемещение образующей может быть подчинено какому-нибудь закону или быть случайным. В первом случае поверхность называют закономерной, а во втором — незакономерной. Выделяют три способа образования поверхностей: аналитический (поверхность задается уравнением); каркасный (поверхность задается определенной совокупностью точек и линий); кинематический (поверхность рассматривается как совокупность последовательных положений некоторой линии (образующей), перемещающейся в пространстве по определенному закону. Совокупность геометрических элементов (форма образующей, форма направляющей, закон перемещения образующих) и связей между ними называется определителем поверхности. Определитель поверхности состоит из двух частей: 1) геометрическая часть определителя — совокупность постоянных геометрических элементов и соотношения между ними; 2) алгоритмическая часть определителя — закон, по которому строятся тоски и линии поверхности. В зависимости от формы образующей и закону перемещения поверхности можно приблизительно разделить на группы. Линейчатые поверхности — поверхности, образующей которых является прямая линия. Линейчатые поверхности могут быть: развертываемые поверхности, т.е. после разреза их по образующей можно совместить с плоскостью без разрыва и складок; неразвертываемые поверхности, т.е. их нельзя совместить с плоскостью без разрывов и складок. Нелинейчатые поверхности — поверхности, образующая которых является кривой линией. Нелинейчатые поверхности могут быть: с постоянной образующей — поверхности, образующая которых не изменяет своей формы в процессе образования поверхности; с переменной образующей — поверхности, образующая которых изменяется в процессе образования поверхности. Если представить себе совокупность прямолинейных образующих и совокупность образующих окружностей, то каждая линия одной совокупности пересечет все линии другой совокупности, в результате чего получается каркас данной поверхности. вращения. Поверхности, образованные вращением линии (образующей) вокруг прямой (оси вращения), называются поверхностями вращения. Определитель поверхности вращения включает образующую и ось вращения. При образовании поверхности вращения каждая точка образующей описывает в пространстве окружность. Эти окружности называют параллелями. Плоскости параллелей всегда перпендикулярны к оси вращения. Наибольшую из параллелей называют экватором, наименьшую — горлом поверхности. Плоскость, проходящую через ось поверхности вращения, называют меридиональной плоскостью. Линия пересечения поверхности вращения меридиональной плоскостью называется меридианом поверхности. Если поверхность вращения образована вращением прямой линии, то поучаем линейчатую поверхность, коническую или цилиндрическую. Если поверхность вращения образована вращением кривой линии, то получаем нелинейчатую поверхность, сферу или тор. Сфера — поверхность, образованная вращением окружности вокруг ее диаметра. Тор — поверхность, образованная вращением окружности (или ее дуги) вокруг прямой — оси вращения, размещенной в плоскости окружности и не проходящей через центр окружности. Тор называется замкнутым, если ось вращения пересекается с окружностью, которая образует его, и открытым, если ось вращения не пересекается с окружностью, которая его образует. Эллипсоид вращения образуется вращением эллипса вокруг одной из осей. Параболоид вращения образуется вращением параболы вокруг оси. Гиперболоид вращения образуется вращением гиперболы вокруг оси. При вращении гиперболы вокруг мнимой оси получается однополосный гиперболоид вращения, а при вращении вокруг действительной оси — двуполостный гиперболоид вращения. Положение точки на поверхности вращения определяется при помощи окружности, проходящей через эту точку на поверхности вращения. случай). Способы построения точек пересечения прямой с поверхностью. Через прямую провести вспомогательную плоскость Определить линию пересечения вспомогательной плоскости с заданной поверхностью Определить искомые точки (входа и выхода) как результат пересечения заданной прямой с найденной линией пересеченя Определить видимость 26. Построение линии взаимного пересечения многогранных поверхностей. Линия пересечения двух многогранников — замкнутая пространственная ломаная линия. При ее построении используют два способа. 1. Определяют точки, в которых ребра одной поверхности пересекают грани второй и ребра второй пересекают грани первой (задача на пересечение прямой с плоскостью). Через найденные точки в определенной последовательности проводят линию. При этом можно соединять прямыми проекции точек, лежащих в одной грани. 2. Определить отрезки, по которым грани одной поверхности пересекают грани второй (задача на пересечение двух плоскостей). Если проекция ребра одного из многогранников не пересекает грани второго хотя бы на одной из проекций, то это ребро не пересекает эту грань. 27. Построение линии взаимного пересечения поверхностей вращения. Выбор секущих плоскостей. 28. Способ вспомогательных секущих плоскостей. 30. 29.Особые случаи пересечения поверхностей вращения. Построение линии пересечения поверхностей способом концентрических вспомогательных сфер. Способ концентрических вспомогательных сфер возможно использовать при следующих условиях: пересекающиеся поверхности — поверхности вращения; оси этих поверхностей должны пересекаться; плоскость осей должна быть параллельна одной из плоскостей проекций.

