Zadacha_5-Izgib_balki

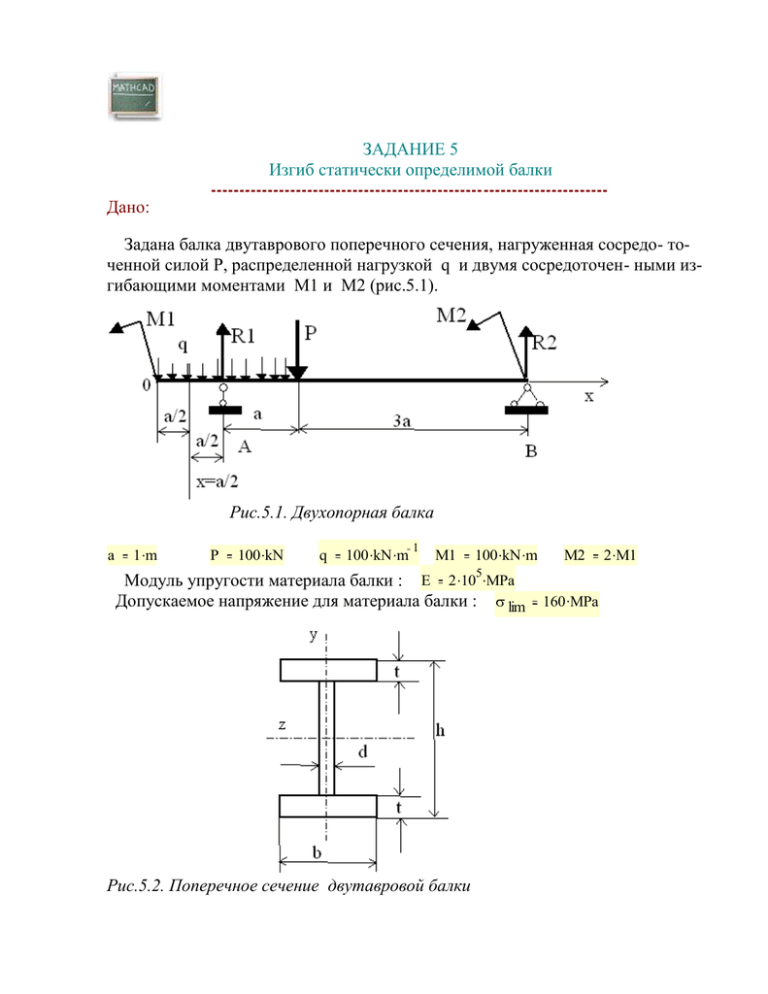
ЗАДАНИЕ 5
Изгиб статически определимой балки
Дано:
Задана балка двутаврового поперечного сечения, нагруженная сосредо- точенной силой Р, распределенной нагрузкой q и двумя сосредоточен- ными изгибающими моментами М1 и М2 (рис.5.1).
Рис.5.1. Двухопорная балка
a
1 m
P
100 kN
q
100 kN m
1
100 kN m
5
2 10 MPa
M1
Модуль упругости материала балки : E
Допускаемое напряжение для материала балки :
Рис.5.2. Поперечное сечение двутавровой балки
 lim
M2
160 MPa
2 M1
Требуется:
1. Найти опорные реакции R1 и R2.
2. Построить эпюры поперечных сил Q и изгибающих моментов M.
3. Подобрать поперечное сечение балки по известному допускаемому
напряжению.
4. Построить эпюры углов поворота сечений балки  и прогибов балки Y.
5. Для сечения, находящегося на расстоянии а/2 от левого конца балки, построить эпюры нормальных () и касательных () напряжений.
6. Провести анализ напряженного состояния в месте перехода полки балки в
стенку.
7. С применением интеграла Мора найти угол поворота сечения в точке В и
прогиб в точке С.
Решение.
1. Для определения опорных реакции R1 и R2 запишем уравнения
равновесия и решим их относительно R1 и R2 с применением функции Find.
Зададим некоторые начальные значения неизвестных реакций:
100 N
R1
R2
200 N
Given
Сумма проекций всех сил на вертикальную ось равна нулю:
R1
R2
P
q 2 a 0
Сумма моментов относительно опоры В равна нулю:
M1
q 2 a 4 a
R1
R2
R1 4 a
P 3 a
M2 0
Find ( R1  R2 )
Таким образом, опорные реакции равны
R1  350 kN
R2  50 kN
2. Переходим к построению эпюр поперечных сил и изгибающих моментов.
Для поперечных сил запишем функцию Q(x) на трех силовых участках и зададим ранжированные значения координаты х , отсчитывая ее от левого конца
балки (рис.5.3).
q x if 0 x a
Q y( x)
q x R1 if a x 2 a
q 2 a
x
R1
P if 2 a x 5 a
0 m 0.02 m 5 a
400
Q y ( x)
200
kN
0
200
4
3
2
1
0
5
x
m
Рис.5.3. Эпюра поперечных сил
Запишем теперь зависимость изгибающего момента от координаты
сечения (рис.5.4).
M z( x)
2
M1
q
x
M1
q
x
M1
q 2 a ( x a )
2
2
2
if 0 x a
R1 ( x a ) if a x 2 a
R1 ( x a )
P ( x 2 a ) if 2 a x 5 a
200
M z( x)
kN m
0
200
0
1
2
3
4
5
x
m
Рис.4.4. Эпюра изгибающих моментов
3. Найдем поперечное сечение двутавровой балки, которое удовлетворит
условиям прочности балки. Максимальное напряжение возникает в сечении над
опорой В при х=5а. Оно не должно превышать допускаемого напряжения, поэтому требуемое значение момента сопротивления сечения изгибу W будет:
Wz
M z( 5 a )
 lim
3 3
W z  1.25 10 m
Анализ справочных данных по двутавровым балкам показывает, что
наиболее близок к расчетному значению момент сопротивления профиляля
№ 45. Этот профиль имеет следующие размеры и моменты I и W:
450 mm
h
160 mm
d
4
27450 cm
b
Iz
8.6 mm
t
14.2 mm
3
1220 cm
W
4. Теперь, когда размеры сечения нам известны, можно приступить к исследованию деформаций балки. Угол поворота сечения есть интеграл от эпюры изгибающих моментов, деленной на жесткость сечения EI. Прогиб балки будет
интеграл от угла поворота сечения
x
 ( x)
M z( x)
EI z
x
d x C1
 ( x) d x C2
Y( x)
0
0
x
x
M z( x)
Y( x)
EI z
0
d x d x C1 x C2
0
Постоянные интегрирования определим из условия равенства нулю прогиба
Y(x) на опорах при x=a и при x=5a . Это даст систему из двух уравнений, которую мы решим относительно С1 и С2 с применением функции Find. Зададим
начальные значения постоянных интегрирования:
C1
2
10 rad
C2
3
10 mm
Given
Для левой опоры
a
x
M z( x)
EI z
0
Для правой опоры
5 a
x
0
C2
C2 0
0
M z( x)
EI z
C1
d x d x C1 a
d x d x C1 5 a
C2 0
0
Find ( C1  C2 )
C1  8.147 10
4
C2  0.172 mm
Построим эпюру углов поворота сечения (рис.5.5).
x
 ( x)
0  0.1 m 5 a
x
M z( x)
d x C1
EI z
0
0.25
( x)
0.1
deg
0.05
0.2
0
1.67
3.33
5
x
m
Рис.5.5. Эпюра углов поворота сечений
Построим эпюру прогибов (упругую линию балки) Y(x) (рис.5.6).
x
 ( x) d x C2
Y( x)
0
2
Y( x)
0
mm
2
4
0
1
2
3
4
5
x
m
Рис.5.6. Эпюра прогибов балки
5. Переходим к построению эпюр нормальных и касательных напряжений в
сечении x=a/2. Нормальные напряжения в этом сечении равны (рис.5.7).
( y)
Mz
a y
2 Iz
Зададим ранжированную переменную y:
y
h
h h
 0.96  
2
2 2
40
20
y
cm
0
20
40
100
50
0
50
100
( y )
MPa
Рис.5.7. Эпюра нормальных напряжений
Касательные напряжения в этом же сечении зависят от координаты y
следующим образом:
Q
 ( y)
a 
S ( y)
2
,
I b1 ( y)
где S(y) - статический момент инерции той части площади поперечного сечения, которая расположена выше уровня координаты y , b1(y) - ширина сечения
балки на уровне y . Запишем функции b1(y) и S(y) для данного сечения двутавра (рис.5.2). Для этого введем следующее обозначение:
h1
h
t
2
Тогда
b1 ( y)
b if
d if
h
2
y h1
h1 y h1
b if h1 y
h
2
0 m otherwise
0.2
y
0
0.2
0
0.05
0.1
0.15
0.2
b1( y )
Рис.5.8. График функции, описывающей сечение двутавра
2
b  h
2
2
S ( y)
b h
2
2
if
2
d
h1
2
b 
2
2
y
h
2
2
2
h
y h1
2
2
h1
2
2
h1
h1
2
y
if
2
y
h1 y h1
if h1 y
h
2
3
0 m otherwise
Построим теперь эпюру касательных напряжений (рис.5.9) .
 ( y)
a 
S ( y)
2
I zb1 ( y)
Qy
40
20
y
cm
0
20
40
15
10
5
0
( y)
MPa
Рис.5.9. Эпюра касательных напряжений
6. Определим теперь значения и направления главных напряжений в месте
перехода полки двутавра в его стенку. Для этой точки координата y1 чуть
больше (-h1). Поэтому положим:
h
y1
1.01 t
2
y1  0.211 m
Вычислим значения нормального и касательного напряжений в этой точке
x
y
( y1 )
0 MPa
 xy
 ( y1 )
 x  86.335 MPa
 xy  10.491 MPa
Главные напряжения в этой точке будут равны:
1
2
x y
x y
2
2
x y
x y
2
2
2
2
 xy
1  87.592 MPa
2
2
 xy
2  1.257 MPa
Направление первого главного напряжения 1 определяется углом  между
осью х и вектором этого главного напряжения:

 xy
1
atan 2 
2
x y
  6.83 deg
Построим круг Мора для напряжений в заданной точке (рис.5.10).
Круг Мора в координатах (   ) определяется его радиусом R и смещением
центра окружности А по оси напряжений

2
R
(
A)
2
2
R
x y
x y
A
2
A  43.168 MPa
2
2
R  44.424 MPa
 xy
2
Для верхней полуокружности имеем:
1 ( )
2
(
R
A)
2
Запишем такую же функциональную зависимость между нормальными и касательными напряжениями для нижней полуокружности:
2 ( )
2
R
(
A)
2
Уравнение для диаметра круга Мора, который проходит через центр окружности и точки с координатами  x   xy и  y   xy имеет вид
 xy
 ( )
x A
( 
A)
Зададим ранжированную переменную 

1.1 2  1.095 2  1 1.1
60
1(  )
MPa
40
2(  )
MPa
20
 xy
MPa
0
 xy
MPa
20
 (  )
MPa
40
60
20
0
20

40
x
80
100
y


MPa MPa MPa MPa MPa


60


Рис.5.10. Круг Mора для напряжений в заданной точке.
Точка пересечения прямой с окружностью имеет координаты, равные
нормальным и касательным напряжениям в месте перехода полки в стенку
7.1. Определение угла поворота сечения в точке В.
Приложим в точке В единичный изгибающий момент и построим эпюру
соответствующих изгибающих моментов (рис.5.11)
Рис.5.11. Балка, нагруженная единичным изгибающим моментом
Найдем опорные реакции
Rm1
0.58 m
1
0.5 m
Rm2
1
Given
Rm1 Rm2 0
Rm1 4 a 1 0
Rm1
Find ( Rm1  Rm2 )
Rm2
1
1
Rm1  0.25
Rm2  0.25
m
m
Построим соответствующую эпюру изгибающих моментов (рис.5.12)
0 if 0 x a
Rm1 ( x a ) if a x 5 a
Mm z( x)
x
0 m 0.02 m 5 a
1
Mm z( x)
m
0.5
0
0
1
2
3
4
5
x
m
Рис.5.12. Эпюра изгибающих моментов от единичного момента в точке В
Угол поворота сечения В будет равен
5 a
B
M z( x) Mm z( x)
EI z
 B  0.273 deg
dx
0
Из эпюры углов поворота сечения (рис.5.5) получаем.
1 B
( 5 a )
1 B  0.273 deg
Значения углов поворота сечения В, найденные различными методами,
совпадают.
7.2. Определение прогиба балки в сечении С.
Приложим в точке С единичную силу (рис.5.13) и построим эпюру соответствующих изгибающих моментов
Рис.5.13. Балка, нагруженная единичной силой
Найдем опорные реакции
Rp1
0.58
Rp2
0.5
Given
Rp1 Rp2 1 0
Rp1 4 a 1 3 a 0
Rp1
Rp2
Find ( Rp1  Rp2 )
Rp1  0.75
Rp2  0.25
Построим соответствующую эпюру изгибающих моментов (рис.5.14)
0 if 0 x a
Mp z( x)
Rp1 ( x a ) if a x 2 a
Rp1 ( x a )
1 ( x 2 a ) if 2 a x 5 a
1
Mp z( x) 0.5
0
0
1
2
3
4
5
x
m
Рис.5.14. Эпюра изгибающих моментов от единичной силы в сечении С
Прогиб балки в точке С будет равен
5 a
C
M z( x) Mp z( x)
EI z
dx
 C  1.992 mm
0
Из эпюры прогибов балки (рис.4.6) получаем.
1 С
Y( 2 a )
1 С  1.993 mm
Абсолютные значения прогибов сечения С, найденные различными методами,
совпадают.
Задача решена
Перход к содержанию