Применение производной к исследованию функций и
advertisement
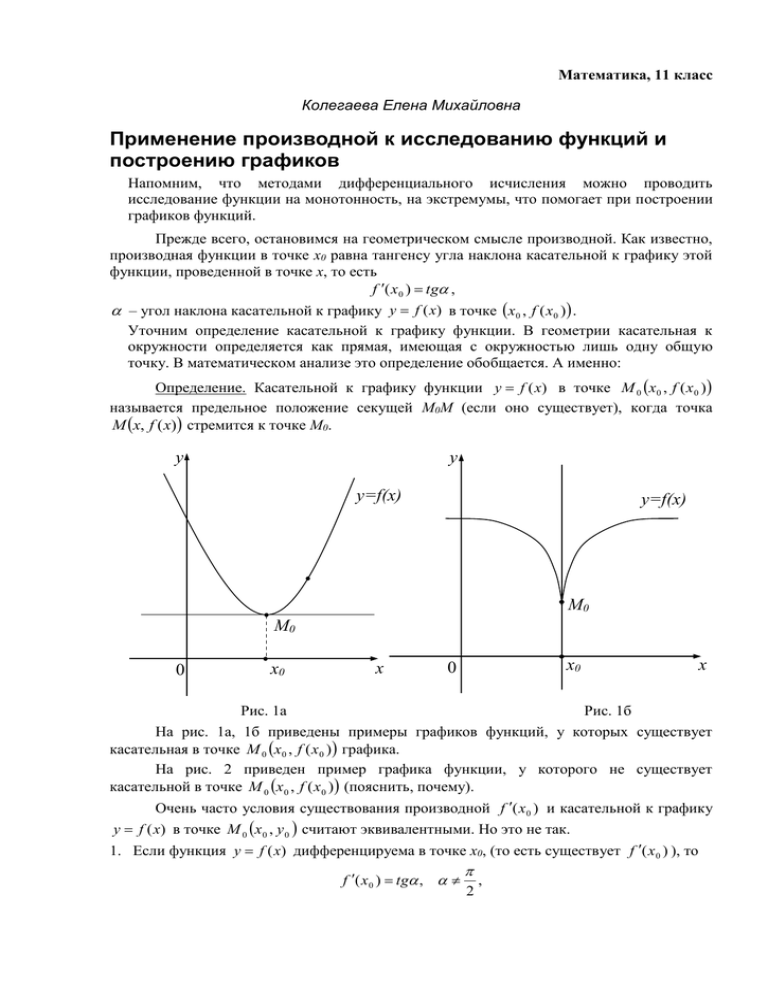
Математика, 11 класс Колегаева Елена Михайловна Применение производной к исследованию функций и построению графиков Напомним, что методами дифференциального исчисления можно проводить исследование функции на монотонность, на экстремумы, что помогает при построении графиков функций. Прежде всего, остановимся на геометрическом смысле производной. Как известно, производная функции в точке х0 равна тангенсу угла наклона касательной к графику этой функции, проведенной в точке х, то есть f ( x 0 ) tg , – угол наклона касательной к графику y f (x) в точке x0 , f ( x 0 ) . Уточним определение касательной к графику функции. В геометрии касательная к окружности определяется как прямая, имеющая с окружностью лишь одну общую точку. В математическом анализе это определение обобщается. А именно: Определение. Касательной к графику функции y f (x) в точке M 0 x0 , f ( x0 ) называется предельное положение секущей М0М (если оно существует), когда точка M x, f ( x) стремится к точке М0. у у y=f(x) y=f(x) M0 M0 0 x0 х 0 x0 х Рис. 1а Рис. 1б На рис. 1а, 1б приведены примеры графиков функций, у которых существует касательная в точке M 0 x0 , f ( x0 ) графика. На рис. 2 приведен пример графика функции, у которого не существует касательной в точке M 0 x0 , f ( x0 ) (пояснить, почему). Очень часто условия существования производной f ( x 0 ) и касательной к графику y f (x) в точке M 0 x 0 , y 0 считают эквивалентными. Но это не так. 1. Если функция y f (x) дифференцируема в точке х0, (то есть существует f ( x 0 ) ), то f ( x 0 ) tg , , 2 то есть, существует невертикальная у касательная к графику y f (x) в точке х0 (рис. 1а). 2. Если же касательная к графику y f (x) в точке М0 существует и является прямой х=х0, то в точке х0 не будет существовать f ( x 0 ) (рис. 1б). Кроме того, как видно из рис. 1б, в точке х0 функция имеет минимум, но не существует f ( x 0 ) . Будем учитывать этот факт в дальнейшем. 0 y=f(x) M0 x0 Рис. 2 х Условия монотонности функции 1. Если функция y f (x) дифференцируема и возрастает на (a, b) (убывает на (a, b)), то f ( x 0 ) 0 при х(a, b) ( f ( x 0 ) 0 при х(a, b)). Верно и обратное: 2. Если функция y f (x) дифференцируема на (a, b) и f ( x 0 ) 0 ( f ( x 0 ) 0 ), то функция y f (x) возрастает (убывает) на (a, b). 3. Если функция y f (x) непрерывна на [a, b], дифференцируема на (a, b) и f ( x 0 ) 0 для х(a; b) ( f ( x 0 ) 0 для х(a, b)), то функция f (x) возрастает (убывает) на [a, b]. Утверждение (2) демонстрируется рис 1а. Функция y f (x) – дифференцируема на (–; +). Так как f ( x 0 ) 0 при х(–; х0), то y f (x) убывает на (–; х0) и так как f ( x 0 ) 0 при х( х0; +), то y f (x) возрастает на ( х0; +). Утверждение (3) демонстрирует рис 1б, а именно: функция y f (x) – непрерывна, но не является дифференцируемой в точке х0 (в этой точке график имеет вертикальную касательную); на промежутке х(–; х0) f ( x 0 ) 0 y f (x) – убывает на (–; х0). Аналогично, на промежутке х( х0; +) f ( x 0 ) 0 y f (x) – возрастает на ( х0; +). Пример 1. Найти все значения параметра а, при которых функция y x 3 ax 3 возрастает на всей числовой прямой. Решение. Найдем f (x) . Имеем f ( x) 3x 2 a . Если f ( x 0 ) 0 для всех x R , то функция возрастает на всей числовой прямой, то есть 3x 2 a 0 . Так как 3 x 2 0 при всех x R , то неравенство выполняется, если a 0 . Ответ: при a 0 функция y x 3 ax 3 возрастает на всей числовой прямой. Пример 2. По графику функции f, изображенной на рисунке 3, определить: а) промежутки, где f ( x 0 ) 0 ; б) промежутки, где f ( x 0 ) 0 ; в) точки, где f ( x 0 ) 0 ; г) точки, где f ( x 0 ) не существует. у k a c 0 b d х у=f(x) e l Решение. а) Если функция возрастает на некотором интервале, то на нем f ( x 0 ) 0 . Поэтому f ( x 0 ) 0 при x ; b k ; l . б) Если функция убывает на некотором промежутке, то на нем f ( x 0 ) 0 . Поэтому f ( x 0 ) 0 при x b; k l; . в) Производная функции связана с касательной f ( x 0 ) 0 . В тех точках, где tg 0 , то есть 0 (касательная параллельна оси Ох). Поэтому, f (b) 0 и f (k ) 0 . г) Аналогично предыдущему, производная не существует в точках, где касательная перпендикулярна оси Ох, то есть, не существует f (l ) . Исследование функции на экстремум Определение. Точка х=х0 называется точкой минимума функции y f (x) , если существует некоторый интервал x0 ; x0 , в каждой точке х которого f ( x) f ( x0 ) (точка х0 на рис. 1а, 1б). у=f(x) у у х0 0 х Рис. 3 0 у=f(x) х0 х Определение. Точка х0 называется точкой максимума функции y f (x) , если существует некоторый интервал x0 ; x0 , в каждой точке х которого f ( x) f ( x0 ) (точки b, l на рис. 3). Необходимое условие экстремума Если х0 – точка экстремума функции, то либо f ( x 0 ) 0 , либо не существует производной в этой точке (такие точки называют стационарными). Замечание. Это условие является необходимым, но не достаточным условием экстремума. Может быть так, что в точке х0 f ( x 0 ) 0 (рис. 4а) или не существует f ( x 0 ) (рис. 4б), и в этой точке функция не имеет экстремума. Поэтому рассмотрим Достаточные условия экстремума Пусть функция y f (x) дифференцируема на интервалах (а; х0) и (х0; b) и х0 – стационарная точка. Тогда: 1. Если при переходе через точку х0 производная f (x) меняет знак с «–» на «+», то х0 – точка минимума функции. 2. Если при переходе через точку х0 производная меняет знак с «+» на «–», то х0 – точка максимума функции. Результаты исследования обычно заносятся в таблицу. Алгоритм исследования функции на экстремум 1. Найти f (x) . 2. Найти точки, в которых: f ( x) 0 или f (x) – не существует. 3. Все точки нанести на числовую прямую и найти знаки производной на каждом из полученных интервалов. 4. Занести результаты в таблицу, например: х f (x) f (x) (–; х1) – х1 0 min (х1; х2) + х2 Не сущ. Нет экстр. … + f min ( x1 ) f ( x1 ) Пример 3. Исследовать функцию на экстремум и построить схематично график. а) y x 3 3x 2 3x ; б) y 3 ( x 2) 2 . Решение. а) y x 3 3x 2 3x . 1) Найдем f ( x) 3x 2 6 x 3 3( x 2 2 x 1) . 2) Найдем точки, в которых f ( x) 0 (функция дифференцируема для всех х). 3( x 2 2 x 1) 0 ( x 1) 2 0 x1 x2 1 . + + 1 х 3) В данном случае удобно воспользоваться исследованием знака f (x) на числовой прямой. Таким образом, в точке х=1 нет экстремума, но в этой точке f (1) 0 , то есть касательная параллельна оси Ох, f (1) 1 . Чтобы построить график, найдем дополнительные точки. Точки пересечения с осью Ох: f ( x) 0 x 3 3x 2 3x 0 x x 2 3x 3 0 . x 0 или x 2 3 x 3 0 – уравнение не имеет решений. Строим график. у у y x 3 3x 2 3x y 3 ( x 2) 2 4 1 1 0 х 1 а) 1 0 Рис. 4 2 3 4 х б) б) y 3 ( x 2) 2 . 1) Найдем y ( x) f (x ) f (x ) 1 2 2 . ( x 2) 3 3 3 3 x2 – + 2 min 2) f ( x) 0 ни в одной точке. f (x) не существует, если х=2. В этой точке функция существует. 3) f min (2) 3 (2 2) 2 0 . Отметим, что в точке х=2 касательная параллельна оси Оу. Найдем дополнительные точки: Точку пересечения графика с осью Оу: f (0) 3 (0 2) 2 3 4 . Задание для самостоятельного решения Уважаемы ребята! Для учащихся 11 классов эта сессия заочной школы является итоговой. После ее завершения педагогический совет ХКЗФМШ примет решение о выдаче вам соответствующих документов. Однако, учебный год продолжается, и в следующем номере будут опубликованы для вас материалы для подготовки к выпускным и вступительным экзаменам. Желаем удачи! Ниже приводятся тексты заданий для самостоятельного решения. Вам необходимо решить эти задачи, оформить решения отдельно от решений по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы. Схематически построить график функции, если известны данные, приведенные в таблице: М11.11.1. х x 2 x 2 2 x2 x2 x2 – 0 – 0 + f (x) f (x) Нет экстр. min f min (2) 3 . Дополнительные точки: f (2) 1; f (0) 0; f (4) 0 . М11.11.2. х f (x) f (x) x 1 + x 1 Не сущ. Max 1 x 3 – x 3 0 min x 3 + f max (1) 4; f min (3) 1 . Дополнительные точки: f (2) 0; f (0) 0; f (4) 0 . Найти все значения параметра а, при каждом из которых функция М11.11.3. y 2 x 5 5ax 4 10 x 3 – всюду возрастает; М11.11.4. y 2 x 3 3(a 3) x 2 6 x – всюду возрастает и не имеет стационарных точек. Исследовать функцию на экстремум и схематично построить график 1 1 М11.11.5. y x 5 x 3 ; 5 3 3 М11.11.6. y x x 1 ; М11.11.7. y x 3 2x 2 ; М11.11.8. y 3 x 2 1 ; М11.11.9. y x cos x ; М11.11.10. y 3 x 2 3 x 1 . 2







